新型变厚度柔性铰链的设计与研究
董飞,许勇,王艳,张强强,赵传森
(上海工程技术大学 机械与汽车工程学院,上海 201620)
柔性铰链与传统的刚性铰链相比,具有可以一体化加工、无间隙、无摩擦和抵抗冲击载荷的优点,从而使得柔性铰链的结构更加简化,体积和重量也更加轻便,便于实现装置的高精度运行,同时利用其抵抗冲击载荷的柔性特点可以提升装置在不同环境下的适应能力[1],因此柔性铰链在近三十多年的时间里,得到快速发展,并被广泛应用到精密仪器操作、微纳精密定位和仿生工程等领域[2-5]。
直梁型柔性铰链因其在受到载荷时,应力被分布在整个直梁的长度方向上,因此直梁型柔性铰链具有较大的转动范围,且普遍高于缺口型柔性铰链,但是直梁型柔性铰链的缺点也比较突出,主要体现在铰链的运动过程中,铰链的中心轴漂较大,导致转动精度较低的缺点[6-7]。由于柔性铰链的结构参数以及自身材料,是决定其性能的关键因素,因此为了克服直梁型柔性铰链的缺点,国内外广大学者们提出了多种变厚度柔性铰链,如杨淼等[8]提出的抛物线形变厚度柔性铰链,张志杰等[9]研究的双曲线型柔性铰链,相对传统的直梁型柔性铰链都有较高的转动精度。
针对直梁型柔性铰链的缺点,本文参考缺口型柔性铰链和变厚度柔性铰链的设计思路,提出了一种新型的变厚度柔性铰链,使得变厚度柔性铰链的变形主要集中在柔性铰链的中心位置,从而提高柔性铰链的转动精度。然后基于Euler-Bernoulli梁理论和悬梁臂挠度积分法[10]建立变厚度柔性铰链的力学模型,并通过有限元法对该变厚度柔性铰链的力学模型和变形特性进行分析[11];参考陈贵敏等[12]提出的一种零轴漂大转角交叉弹簧式柔性铰链,以该变厚度柔性铰链的为基本单元搭建出一种具备大转角能力的柔性转动铰链,为大转角、高精度、大载荷柔性铰链的设计提供理论参考。
1 变厚度柔性铰链的设计
本文设计的变厚度柔性铰链的结构如图1所示,首先建立坐标系A-XY,并以坐标(0,-a)为圆心,r为半径画圆弧R1;以坐标(2l,-a)为圆心,r为半径画圆弧R2,圆弧R1与圆弧R2交点的横坐标为B(0,l),然后将圆弧R1与圆弧R2关于X轴对称,形成一个封闭的拥有一个转动自由度的变厚度柔性铰链,此时变厚度柔性铰链为一个非直梁型柔性铰链,应变主要集中在铰链的中心位置B处,该变厚度柔性铰链的中性轴AD与X轴重合,且梁两端的交点为A、D两点。
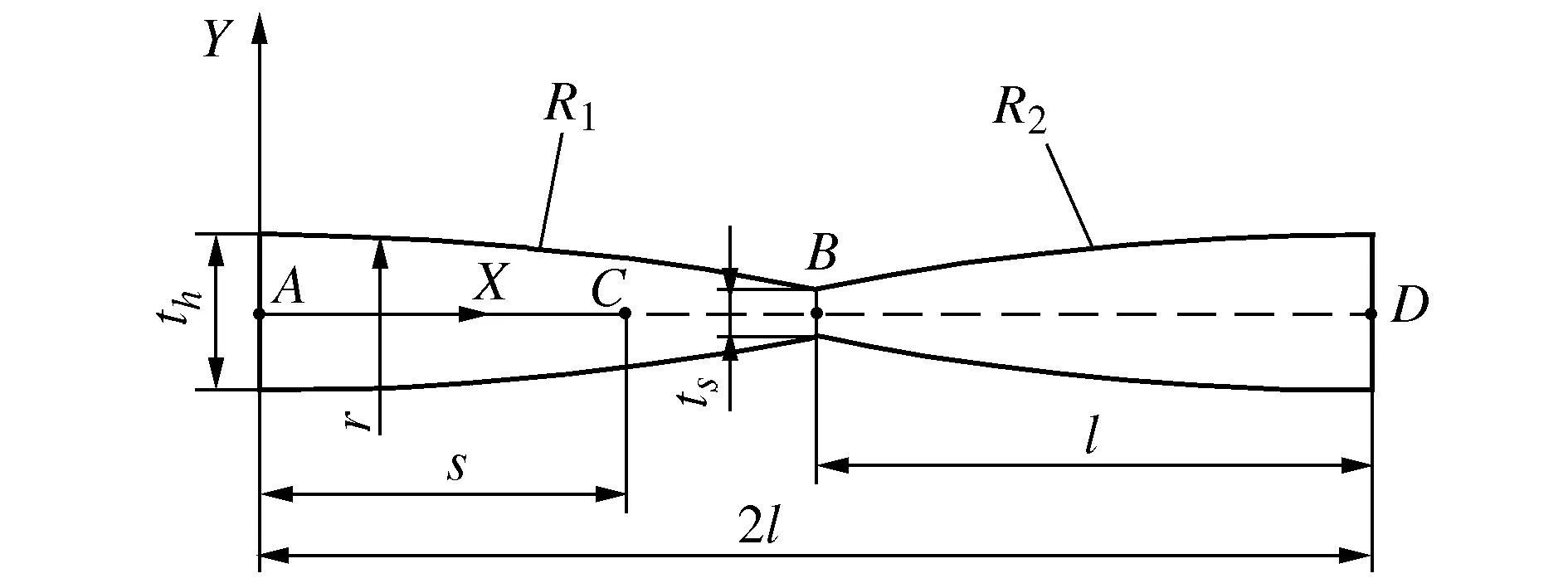
图1 变厚度柔性铰链结构示意图
设该变厚度柔性铰链的最大厚度为th,最小厚度为ts,长度为2l,宽度为w,其中AB=BC=l,如图1所示,由此可以算出中性轴上任意一点C的厚度为:

(1)
式中:s表示中性轴AD上任意一点C到坐标原点A的弧长,在没有载荷作用的情况下,该变厚度柔性铰链的中性轴AD与X轴重合。
2 建立力学模型
将变厚度柔性铰链的A端点固定,D端点作为自由端,变厚度柔性铰链在工作时会受到不同的载荷作用,可以用作用点在D处,平行X轴的力Fx,平行Y轴的力Fy,和转矩方向垂直XAY面的转矩Mz来表示,在受到载荷作用后,变厚度柔性铰链产生变形,可以看成悬臂梁结构,如图2所示。
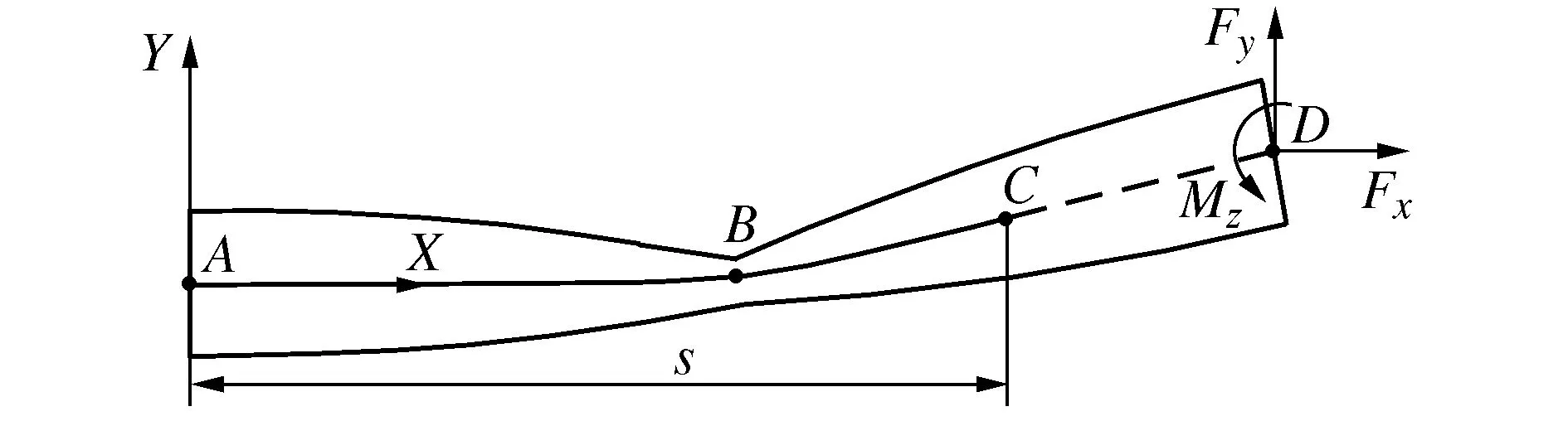
图2 变厚度柔性铰链变形结构示意图
设变厚度柔性铰链变形后D点的坐标为(xd,yd),C点坐标为(x,y),它们的数值与载荷的大小有关,其中曲线AC的弧长为s。则变厚度柔性铰链任意一点C处的力学分析如图3所示。

图3 C处受力分析图
可得:
(2)
由公式(2)可以进一步表示出,变厚度柔性铰链变形后任意一点C处截面受到的最大拉应力为
(3)
式中Ac表示变厚度柔性铰链任意一点C处截面的面积。由式(1)可以得到
Ac=wtc
(4)
根据Euler-Bernoulli 梁理论,中性轴AD上任意一点C的曲率与该点截面处受到的转矩成正比例关系,由此可得:

(5)
为求解公式(5),需要引入变厚度柔性铰链变形的边界条件。在变厚度柔性铰链固定端点A处的边界条件为:
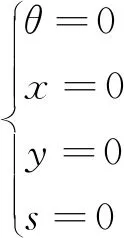
(6)
由于通常情况下D点坐标是未知的,所以这里还需引入以下方程组进行求解:
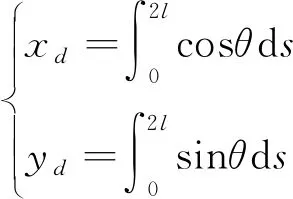
(7)
由式(4)~式(7)组成的非线性方程组,带入具体数值后通过牛顿迭代法[13]进行求解。
3 模型验证
为验证本文力学模型的正确性,采用有限元仿真软件ABAQUS进行有限元验证,在有限元仿真软件中,选用的模型材料为Ti-64AL-4V,材料的弹性模量为104.8 GPa,屈服模量为827.4 MPa,泊松比为0.31,该变厚度柔性铰链的结构参数如表1所示。

表1 变厚度柔性铰链的结构参数
通过在该变厚度柔性铰链的自由末端(D点处)施加不同的预载,得到柔性铰链自由末端在不同转矩Mz作用下的位移变化曲线,如图4~图7所示。
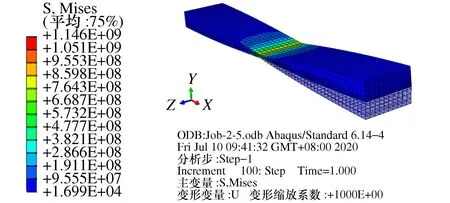
图4 圆弧半径r=150 mm的变厚度柔性铰链仿真示意图
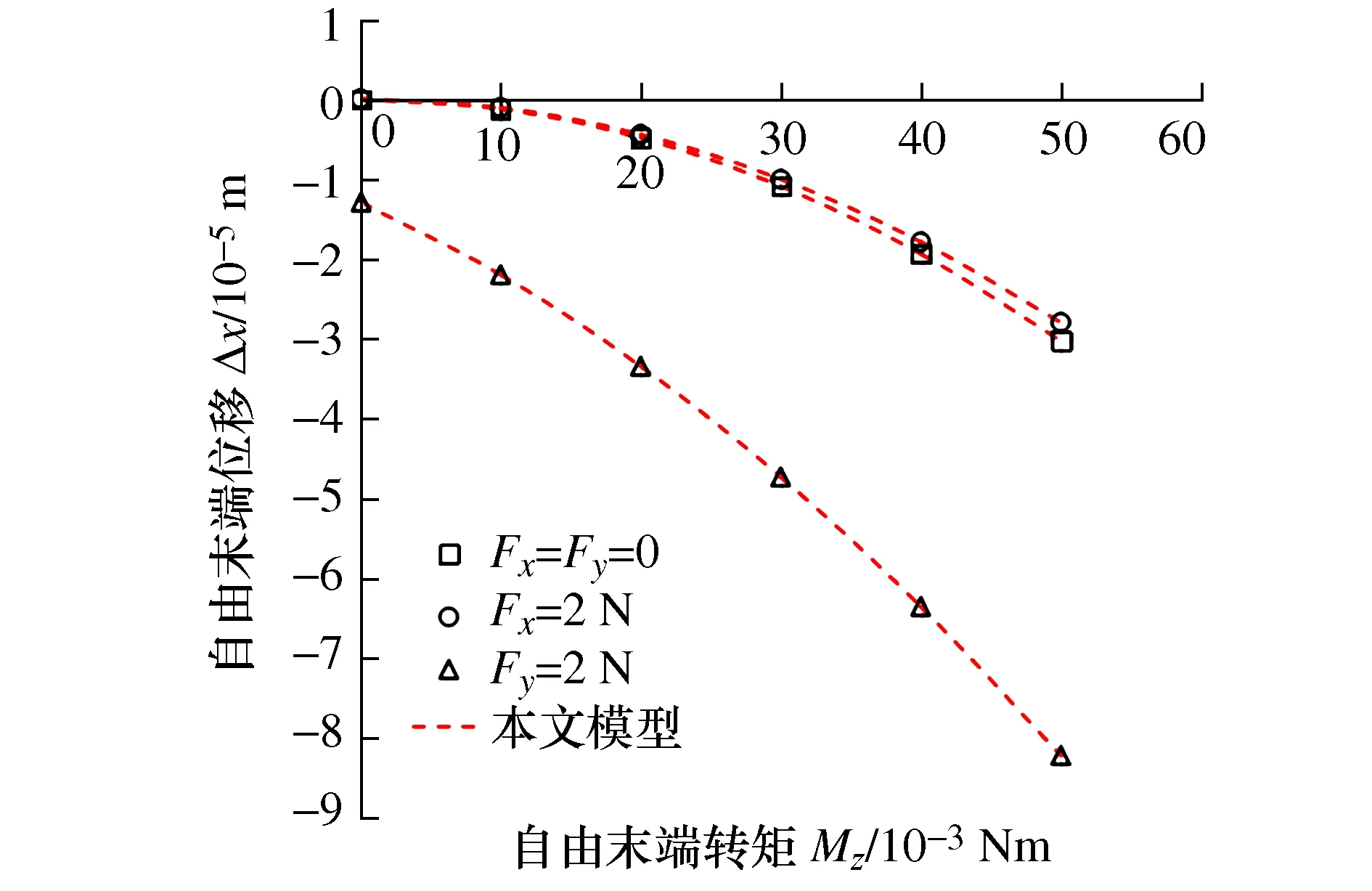
图5 变厚度柔性铰链自由末端X轴方向位移Δx与转矩Mz之间的关系
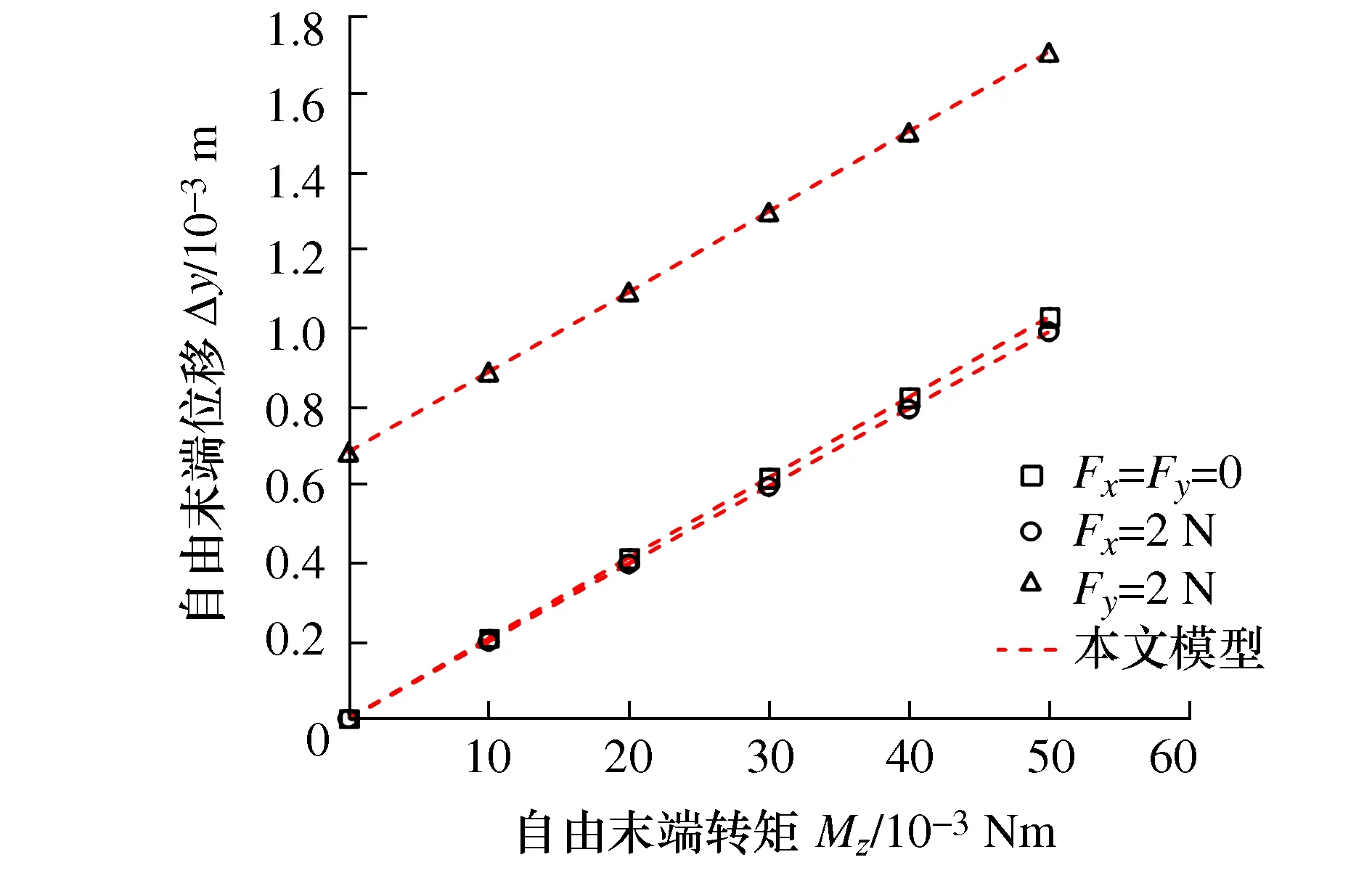
图6 变厚度柔性铰链自由度末端Y轴方向位移Δy与转矩Mz之间的关系
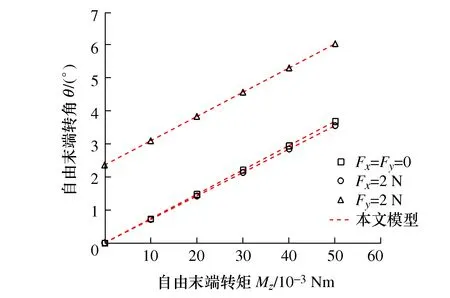
图7 变厚度柔性铰链自由末端转角θ与转矩Mz之间的关系
图4中,在有限元仿真环境中,可以直观的看到变厚度柔性在受到载荷时的变形主要集中在铰链的中心处(B处),通过图5~图7分析得出,变厚度柔性铰链自由末端X轴方向位移Δx与转矩Mz之间呈抛物线关系,自由度末端Y轴方向位移Δy与转矩Mz之间呈正比例关系,自由末端转角θ与转矩Mz之间呈正比例关系,且有限元仿真结果与本文模型匹配程度较好,验证了本文模型的正确性。
4 变厚度柔性铰链的变形特性分析
研究柔性铰链的意义是代替传统刚性铰链,以满足无缝传动的目的,使得机构具备高精度、大转角、无摩擦等优点。因此需要从多个性能指标来评价柔性铰链的性能,通常的评价性能指标包括:转动刚度、转动范围、中心轴漂和抗干扰能力等[14]。变厚度柔性铰链相对传统的直梁型柔性铰链的区别是引入半径为r的圆弧R1、R2构造出变厚度柔性铰链,从而改变了柔性铰链的变形特性,故本文将重点研究分析变厚度柔性铰的变形特性与圆弧半径r之间的关系。
1) 转动刚度:转动刚度的定义为柔性铰链转动过程中受到的转矩与转角之间的比值。
图8表示不同圆弧半径r的变厚度柔性铰链自由末端转角θ随自由末端转矩Mz的变化曲线,通过图7可以看出变厚度柔性铰链自由末端转角θ与自由末端转矩Mz之间成正比例关系,同时圆弧半径r越大,对应的变厚度柔性铰链的曲线斜率越小,说明该变厚度柔性铰链的转动刚度越大。
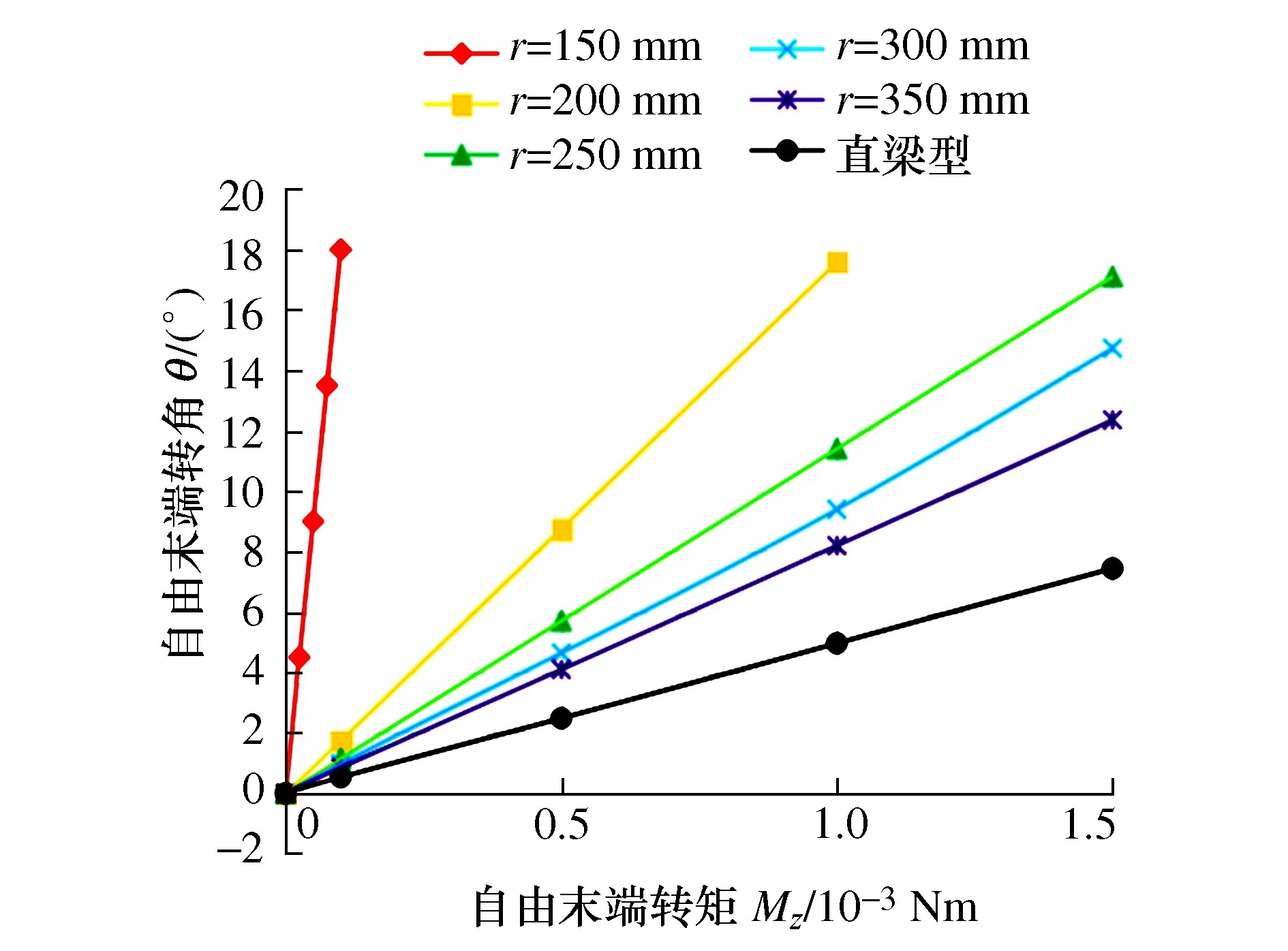
图8 不同圆弧半径r的变厚度柔性铰链自由末端转动角度θ随转矩Mz的变化曲线
2) 转动范围:转动范围即为柔性铰链在受到转矩作用,达到许用应力时该柔性铰链所转动的角度。
图9表示变厚度柔性铰链自由末端转角范围随圆弧半径r的变化曲线,从图9可以得出圆弧半径r越大,对应的变厚度柔性铰链的转角范围越大。对比传统的直梁型柔性铰链(r→∞),在r=150 mm时的变厚度柔性铰链的转动范围为前者的33.9%。
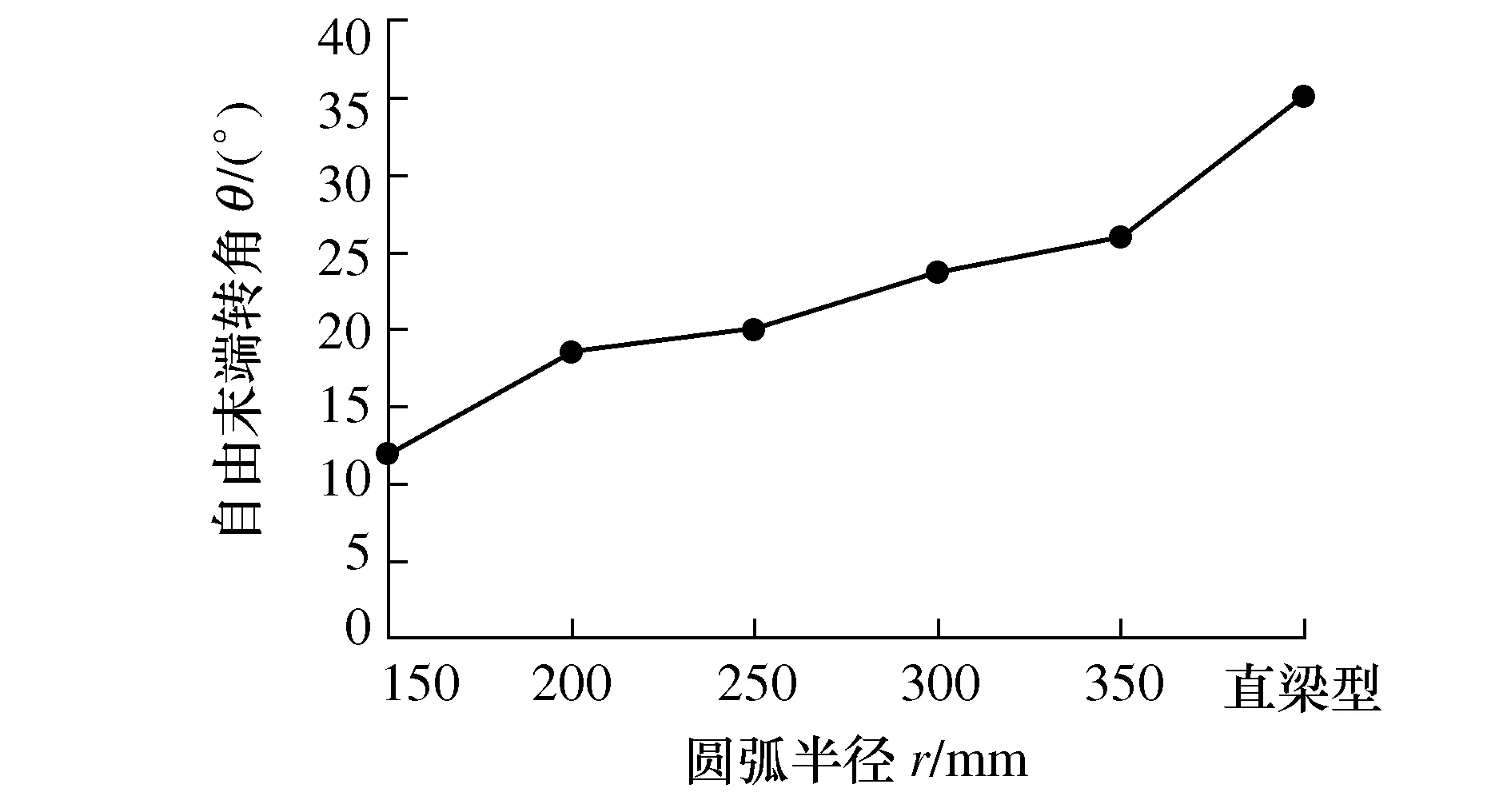
图9 变厚度柔性铰链自由末端转角范围随圆弧半径r的变化曲线
3) 中心轴漂:中心轴漂定义为柔性铰链的实际转动中心与理论转动中心之间的位移差距。中心轴漂越小,表面该柔性铰的转动精度越高。变厚度柔性铰链的中心轴漂n的表达式为
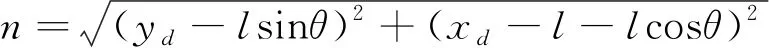
(7)
图10表示不同圆弧半径r的变厚度柔性铰链中心轴漂n随自由末端转角θ的变化曲线,在不同圆弧半径r的变厚度柔性铰链转动到6°的过程中,通过图10分析得出,转角θ越大则变厚度柔性铰链的中心轴漂n越大,在变厚度柔性铰链转动到设定角度时,圆弧半径r越大的变厚度柔性铰链的中心轴漂n也越大。对比传统的的直梁型柔性铰链(r→∞),变厚度柔性柔性铰链(r=150 mm)的中心轴漂n在自由末端转角为6°时铰链的中心轴漂为前者的19.2%,因此使用变厚度柔性铰链作为转动副,可以较为显著的提高柔性铰链的转动精度。

图10 不同圆弧半径r的变厚度柔性铰链中心轴漂n随自由末端转角θ的变化曲线
4) 抗干扰能力:表示柔性铰链在转矩作用下转动到设定角度,受到额外载荷时,以抵抗外部载荷对柔性铰链转动精度影响的能力。因为变厚度柔性铰链的自由末端除了转矩Mz的作用,往往还会受到平行Y轴的力Fy与和X轴平行的力Fx的干扰力,由于Fy在柔性铰链自由末端的作用与Mz的作用相同,而Fx的对柔性铰链的转动精度具有较大影响。因此,柔性铰链的抗干扰能力也可以定义为在柔性铰链转动到设定角度后,自由末端受到Fx作用时,其中心轴漂产生的变动量Δn。
图11表示在变厚度柔性铰链转动角度到6°时,给变厚度柔性铰链的自由末端(D点处)施加干扰力Fx=2 N,得到的变厚度柔性铰链中心轴漂变动量Δn随圆弧半径r的变化曲线,可以分析得出,随着圆弧半径r的增加,变厚度柔性铰链的中心轴漂变动量Δn也越小,抗干扰能力也越强,与传统的直梁型柔性铰链(r→∞)相比,变厚度柔性铰链(r=150 mm)的抗干扰能力为前者的24.3%。
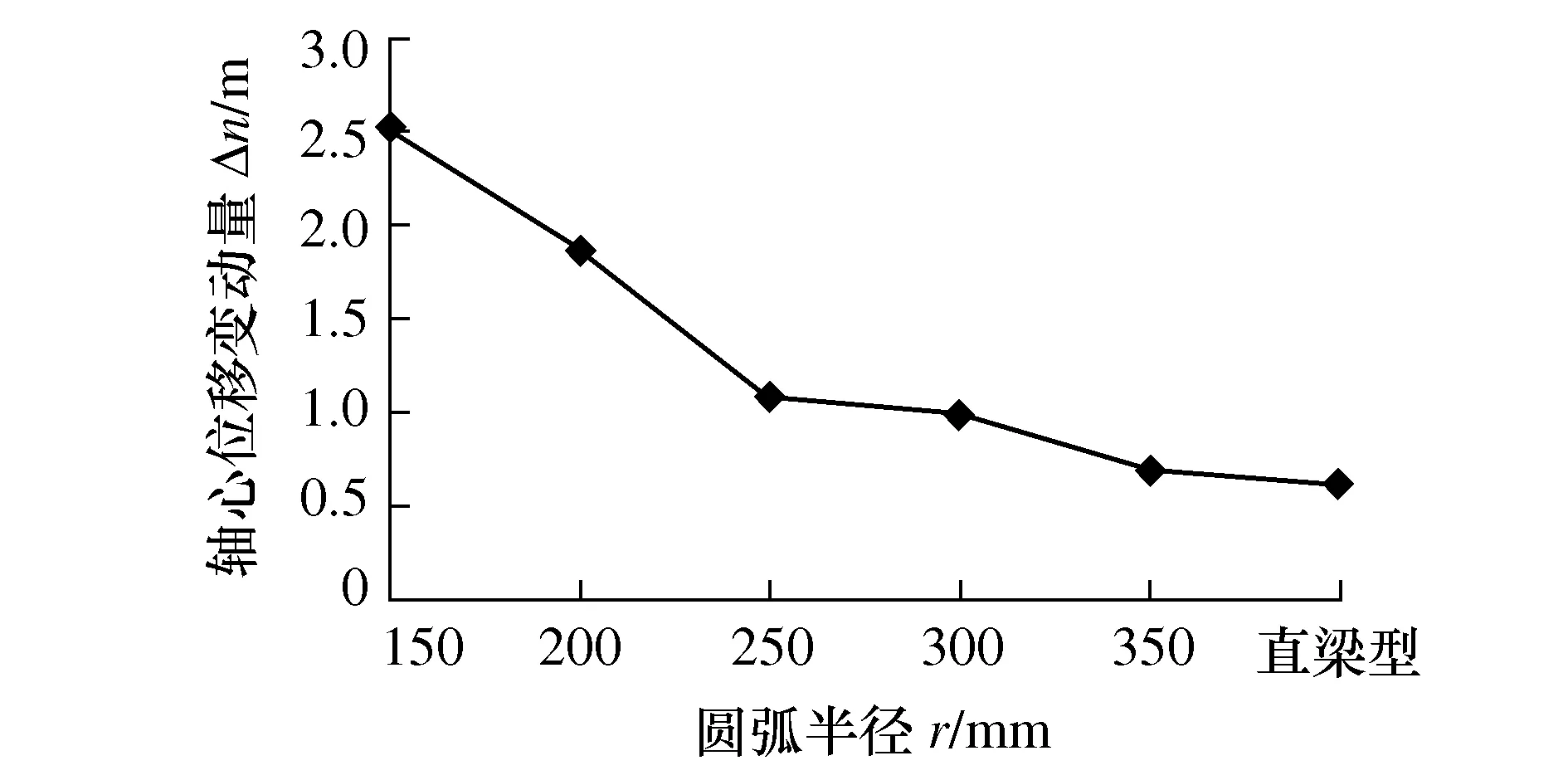
图11 中心轴漂变动量Δn随圆弧半径r的变化曲线
5 应用
前文分析了变厚度柔性铰链的变形特性与圆弧半径r之间的关系,可以看出本文提出的变厚度柔性铰链,比较适合应用在大转角高精度的柔顺机构中。参考陈贵敏等人提出的零轴漂大转角柔性铰链,以变厚度柔性铰链为基本单元,搭建出一种具有大转角能力的柔性转动铰链,如图12所示。
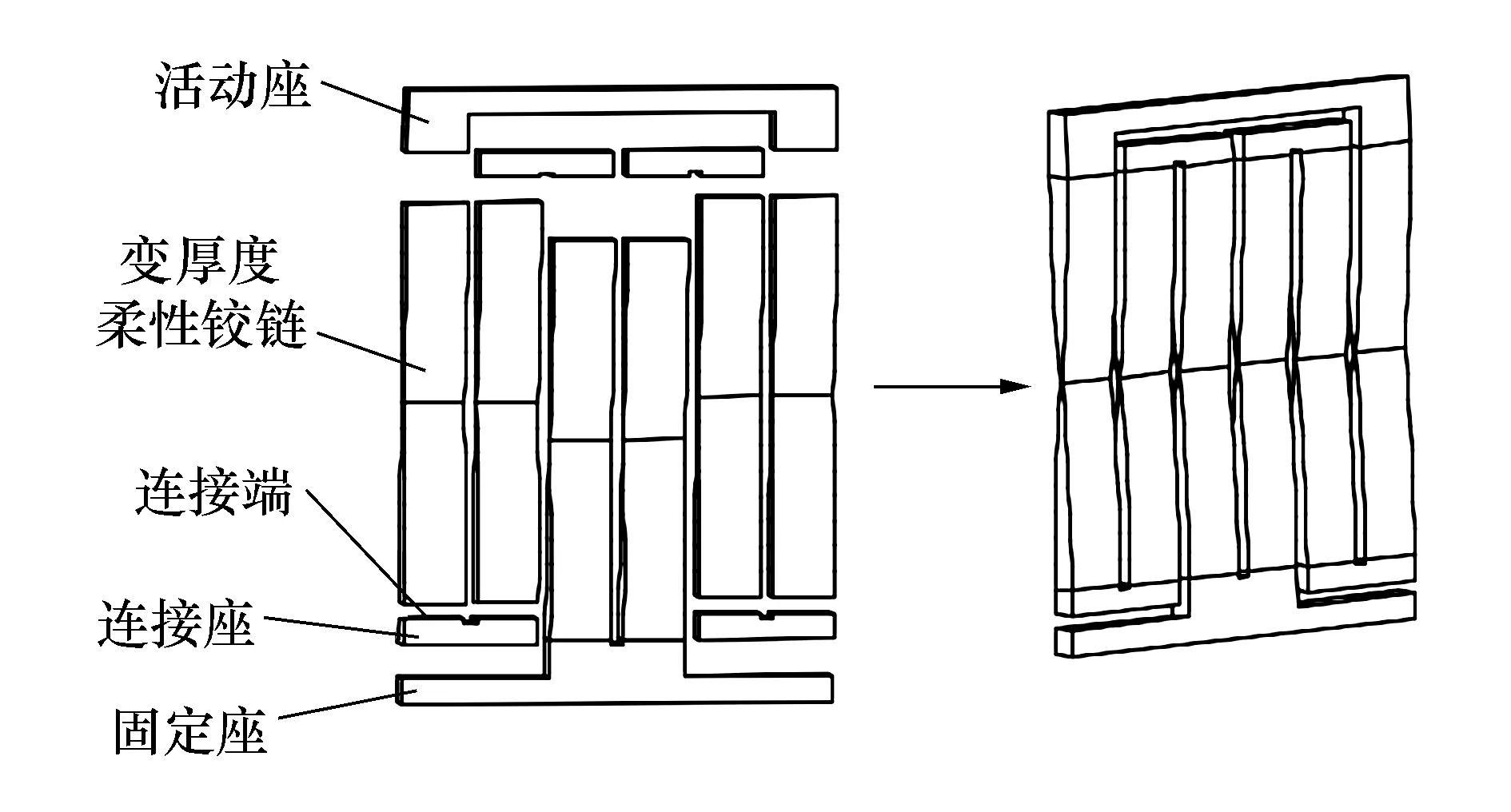
图12 柔性转动铰链结构简图
图12中的柔性转动铰链包括固定座、连接座、变厚度柔性铰链和活动座,固定座的顶端中部的两侧分别设置有连接端,连接座的顶端两侧分别设置有连接端,活动座的底端两侧也分别设置有连接端,固定座的顶端两侧对称设置有连接端向上的连接座,活动座的底端中部对称设置有连接端向下的连接座,且活动座位于固定座上方,活动座底端与固定座顶端平行,然后通过6个变厚度柔性铰链将各连接端依次串连在一起,如图12所示,构成具有大转角能力的柔性转动铰链。
通过力学分析,在该柔性铰链在活动座受到纯转矩Mz作用时,每个变厚度柔性铰链将承受0.5倍的转矩Mz,由于变厚度柔性铰链将各连接端依次串连在一起,所以该新型柔性转动铰链在受到相同转矩Mz的作用下将比单个变厚度柔性铰链的转角大,且承载能力更强。取表1描述的变厚度柔性铰链搭建柔性转动铰链,在有限元软件ABAQUS中仿真得到如图13所示的具备大转角能力的柔性转动铰链仿真示意图和图14所示的转角θ随转矩Mz的变化曲线。

图13 具备大转角能力的柔性转动铰链仿真示意图
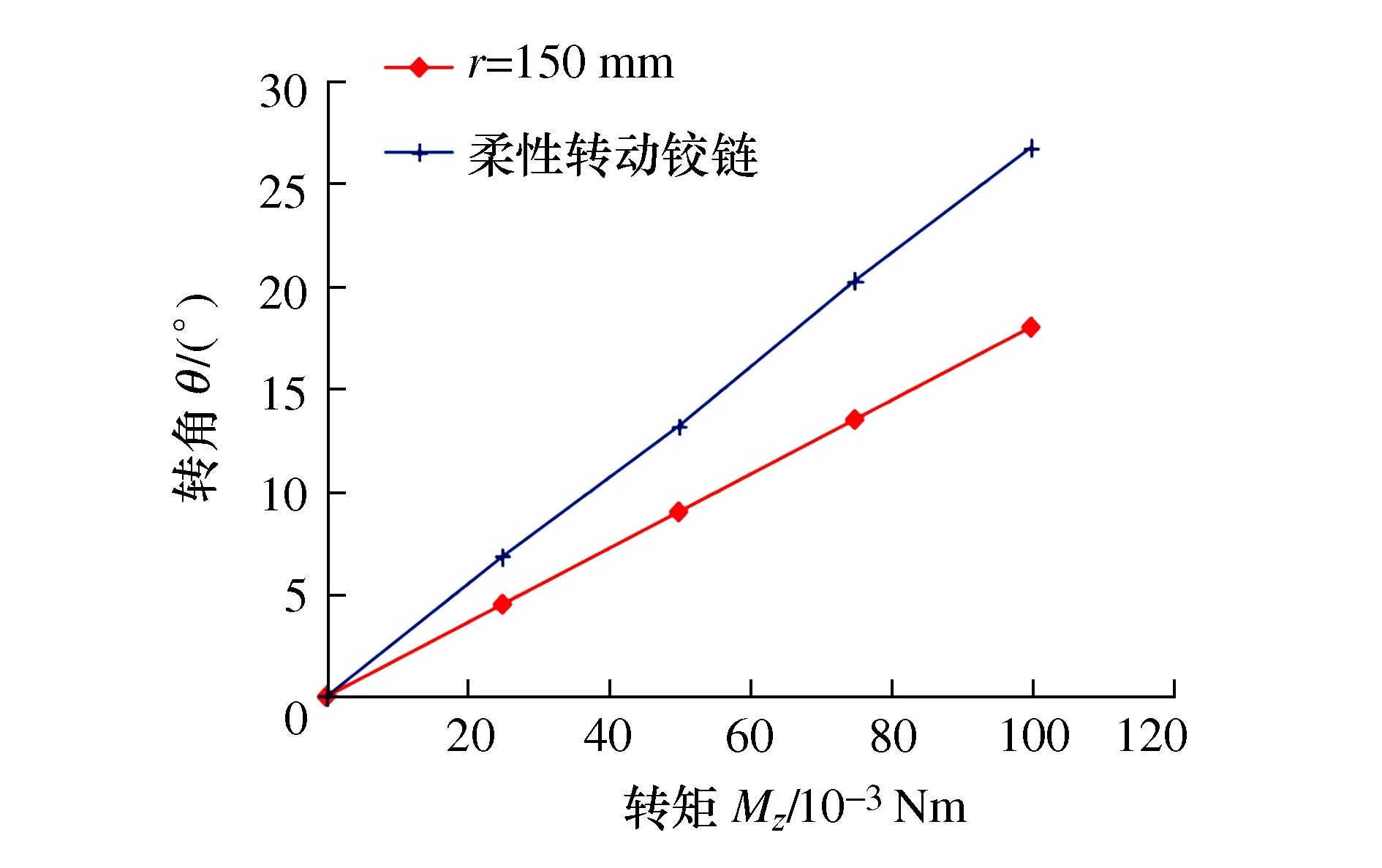
图14 转角θ随转矩Mz的变化曲线
由图13和图14可以看出,在以变厚度柔性铰链为单元搭建出的柔性转动铰链,在相同转矩Mz的作用下,相对于单个变厚度柔性铰链具有更大的转角,柔性转动铰链的转角θ约为单个变厚度柔性铰链的1.5倍。同时,由于柔性转动铰链中的变厚度柔性铰链承受到的载荷只有转矩Mz的0.5倍,所以该柔性转动铰链相对于单个变厚度柔性铰链具有更大的承载力,可以适用于大转角小轴漂、大载荷的工作环境中,对仿生机器人领域的仿生关节的设计,给予一定的理论参考[15-16]。
6 结束语
1) 提出一种新型的变厚度柔性铰链,使得变厚度柔性铰链的变形主要集中在柔性铰链的中心位置,从而改变柔性铰链的转动性能,使其相对传统的直梁型柔性铰链具有更好的转动精度。
2) 基于Euler-Bernoulli梁理论建立变厚度柔性铰链的力学模型,通过牛顿迭代法带入具体数值进行求解。然后将变厚度柔性铰链带入有限元仿真软件ABAQUS中进行仿真,将仿真结果与本文力学模型进行对比,验证了变厚度柔性铰链力学模型的正确性。
3) 通过分析变厚度柔性铰链的圆弧半径r与柔性铰链转动性能之间的关系,结果表明,随着圆弧半径r的逐渐增加,变厚度柔性铰链的转动刚度、转角范围以及抗干扰能力均逐渐增加,中心轴漂n则逐渐减小。
4) 根据变厚度柔性铰链的变形特性分析,以变厚度柔性铰链为单元搭建出一种具备大转角能力的柔性转动铰链,并在仿真软件中进行了验证,为该柔性转动铰链运用到仿生领域提供了参考。
5) 本文未对以变厚度柔性铰链为单元搭建出的一种具备大转角能力的柔性转动铰链进行力学建模,将在后续工作中继续完善。

