焊接结构切口等效应力修正方法研究与应用分析

张哲,王悦东,刘本末

(大连交通大学 机车车辆工程学院,辽宁大连 116028)

铁路车辆在工作过程中,会受到来自轨道的冲击载荷作用,导致结构突变的焊接位置产生应力集中现象,萌生疲劳裂纹,导致疲劳断裂[1-3]。应力集中往往是结构产生疲劳破坏的主要原因之一[4],因此,研究焊接结构截面位置的应力集中现象十分重要,而焊接结构的类型与尺寸对于结构的应力集中有着至关重要的影响。因此,对于主要承受载荷的关键部位,对焊接接头的类型以及尺寸的选取要有确切的把握,使焊接接头的应力集中程度在结构合理的情况下达到相对较低的水平,从而满足焊接结构的疲劳强度以及寿命要求。

Williams[5]在弹性理论的基础上证明了V型角度结构的尖点位置具有应力奇异性,并且奇异应力的大小与V型结构的角度大小关系密切。Yung等[6]对焊接结构的直角突变位置进行了系统的分析,考虑了焊接处拐角半径的影响,来计算真实应力分布,不然就要将拐角位置的应力奇异性纳入考虑范围来分析其焊接疲劳行为。肖林等[7]人采用热点应力法预测疲劳寿命,并将其与9个试件的疲劳实验结果进行比较,证明了焊接细节采用两点外推法与三点外推法计算热点应力均是可行的。廖平等[8]应用ANSYS软件建立有限元模型,研究了钢梁十字焊接结构的焊脚尺寸、过焊孔半径、焊缝宽度等尺寸对各部件应力集中系数的影响,结果表明过焊孔半径对各部件的应力集中系数影响较大。Dong[9]基于自由体的切面法,应用有限元方法计算节点力和弯矩,得到焊接位置的结构应力,以结构应力σs为自变量计算出应力强度因子SIF,将断裂力学作为理论基础,并结合与疲劳寿命相关的应力参数,不仅考虑载荷作用模式以及板厚对疲劳强度产生的影响,也研究了焊接结构突变位置应力集中对疲劳强度的影响,综合了这些影响因子,推导出等效结构应力ΔSs的计算公式。高嵩等[10]研究了焊接接头处应力分布特点,同时针对焊接位置的应力奇异性,研究了焊趾处垂直于裂纹扩展方向的切口应力分布,得到了“奇异应力函数”,并通过线性回归方法得到切口应力的等效取值点xas的函数,从而求出焊接接头处的切口等效应力σy,并研究出了一种仅与焊接接头尺寸相关的“奇异强度as”概念,从而找到了存在应力集中的焊接构件疲劳寿命的另一种简单求解方法:切口应力等效取值法。

为探究切口应力等效取值法在轨道交通领域的适用性,结合典型16Mn材料焊接接头,应用去除应力集中影响因子的切口应力等效取值法、完整切口应力等效取值法和等效结构应力法预测16Mn材料十字焊接接头的疲劳寿命,证明了切口应力等效取值法考虑了应力集中的影响。然后对切口应力等效取值法得到的预测寿命与试验寿命进行对比分析,通过引入切口等效应力修正系数,得到适用于16Mn材料疲劳寿命预测的切口等效应力修正公式。

1 切口等效应力原理

根据实际零件的裂纹上、下表面间相对位移的不同,可将裂纹分为张开型(Ι型)裂纹、滑开型(Ⅱ型)裂纹、撕开型(Ⅲ型)裂纹三种基本形式,其中以Ι型裂纹为主,为了研究Ι型裂纹附近的应力分布,Lazzarin和Tovo[11]在焊接接头中存在线弹性应力梯度的背景下,基于应力强度因子,得到焊接接头焊趾处Ι型裂纹垂直于裂纹方向的应力分布为

(1)

式中:x为到焊趾的距离;KΙ=σn·k1·t1-λ1,σn为均布拉伸名义应力,k1=f(h,t,L),t为受载板厚,L为非受载板厚,h为焊脚尺寸;ϑ为拐角平分线到应力分析线的角度;λ1和χ1为不同角度对应的无量纲参数。

为方便计算,可以将式(1)改写成

(2)

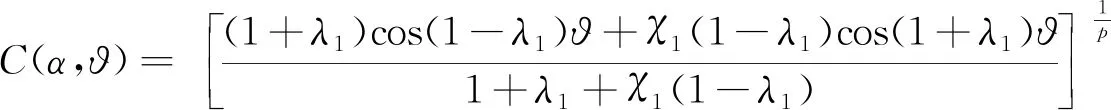
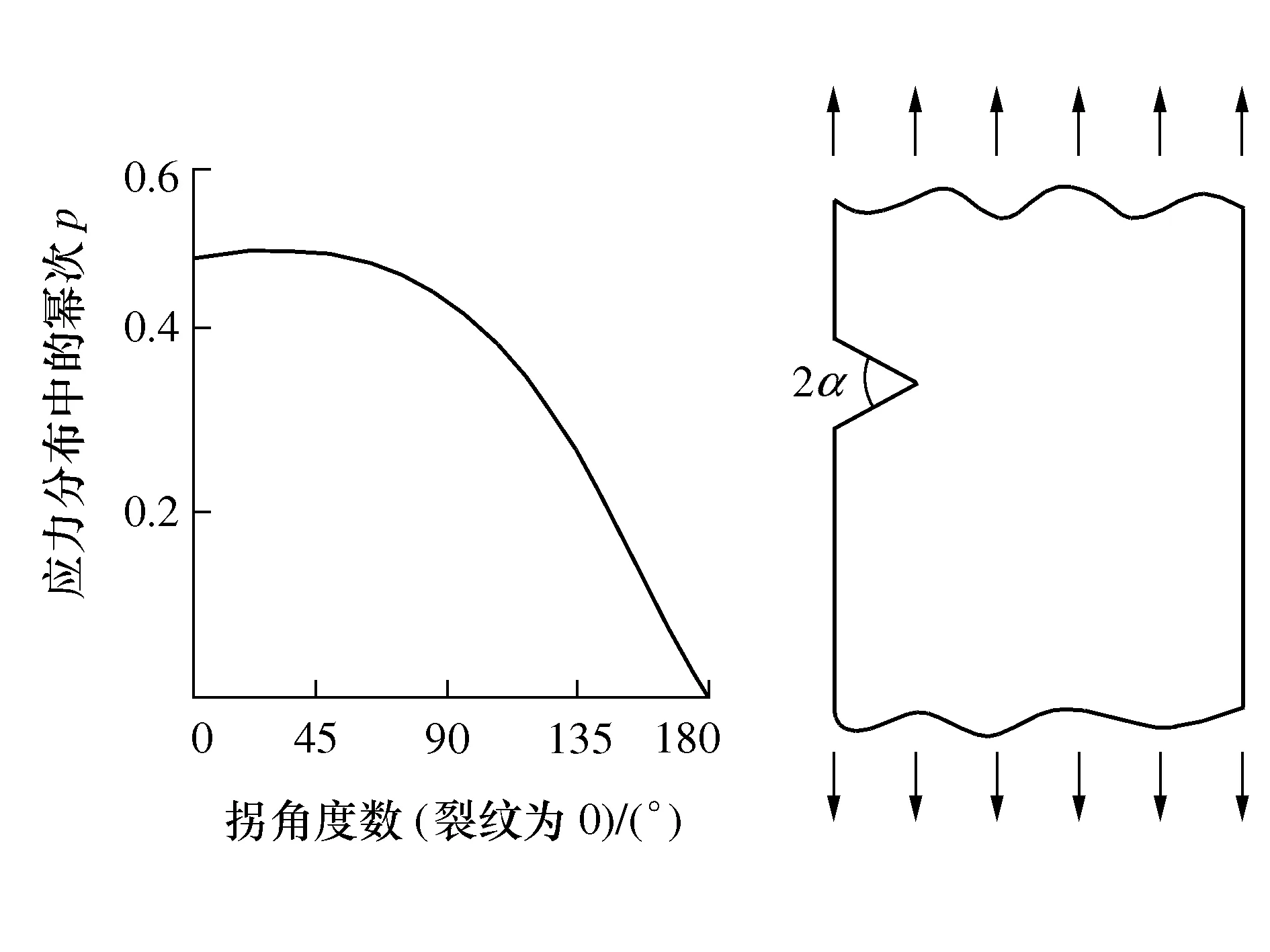
图1 不同拐角对应的p值

当2α=0时,可将拐角视作裂纹,当2α等于其他角度时,可认为拐角处应力分布与裂纹尖端处的应力分布形式相近。Paris和Sih[12]经过计算得到裂纹尖端应力分布的精确解,高嵩等[10]改写其为适用于其它角度的一般形式,并提出奇异强度as的概念,最后用奇异强度as替代公式中的裂纹尺寸a。以此,将应力集中因素考虑在内,得到切口等效应力函数式,即

(3)

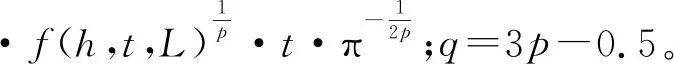
2 考虑焊接结构应力奇异性的疲劳寿命评估方法

2.1 等效结构应力法

美国密歇根大学董平沙教授基于结构应力法,同时结合断裂力学原理,以及不同的板厚、不同的材料、不同类型的焊接接头的试验数据,完成了S-N曲线模型来评估焊缝的疲劳寿命[13]。

等效结构应力法通过在焊线上的节点位置建立局部坐标系,通过等效矩阵的方法将节点力转化为单元线力,从而回避了焊接结构尺寸突变位置对应力集中的影响。等效结构应力的计算是在结构应力的基础上结合断裂力学的知识得到的,其计算公式为

(4)

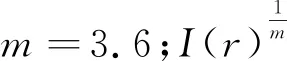
计算出等效结构应力后,可通过主S-N曲线法的主S-N曲线计算焊缝的疲劳寿命,其表达式为

ΔSs=Cd×N-h′

(5)

式中:Cd和h′为试验常数(见表1)。

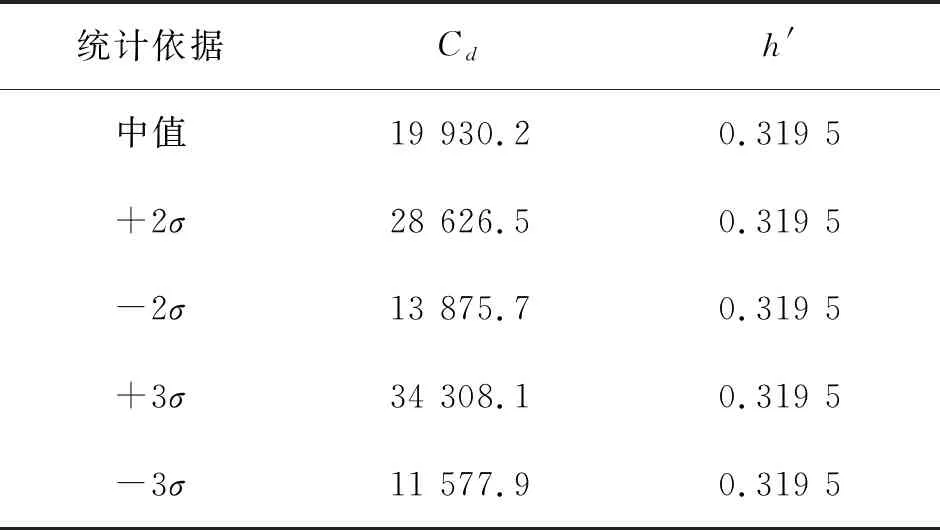
表1 主S-N曲线参数(钢材)

文献[14]中对等效结构应力法的可行性进行了验证,在循环次数为6 863次时,结构发生疲劳破坏;通过等效结构应力法进行计算得到:在存活率均为98%的情况下,发生破坏的寿命为5 574次。试验结果与等效结构应力法计算结果之间误差仅为18.8%,证明了等效结构应力法的可行性。

2.2 切口应力等效取值法

切口应力等效取值法基于切口应力强度因子理论(N-SIF),对Lazzarin和Tovo[11]求解的切口区域的应力场函数进行简化,得到切口等效应力函数式(3),为求得切口等效应力,高嵩等[10]定义了“切口应力等效取值点xas”,并利用Math CAD进行线性回归,得到切口应力等效取值点xas的分段函数式为

xas=A+B·as+C·as2+D·as3+E·as4

(6)

式中:xas和as的单位为mm;A、B、C、D为分段函数式参数,见表2。

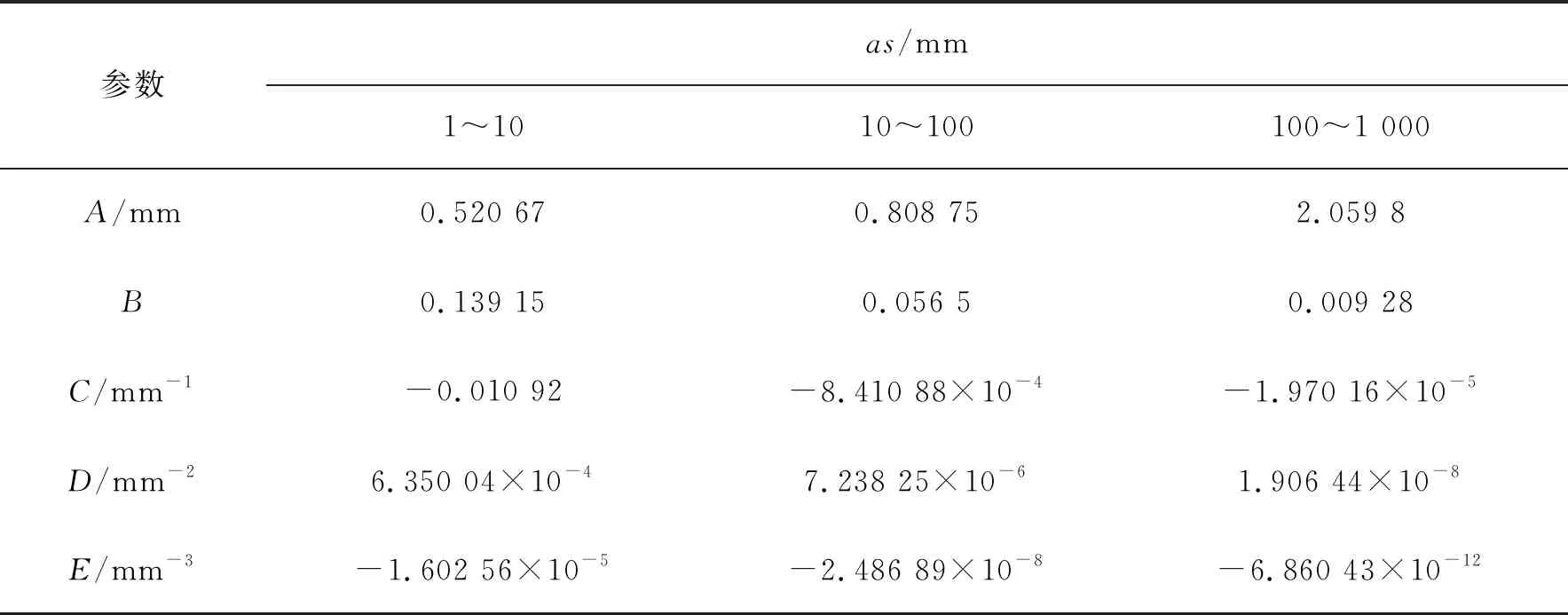
表2 切口应力等效取值点分段函数式参数

焊接结构135°拐角的奇异强度as的计算式[10]为

(7)

式中H为非受载板高。受分析的结构边缘如图2所示。

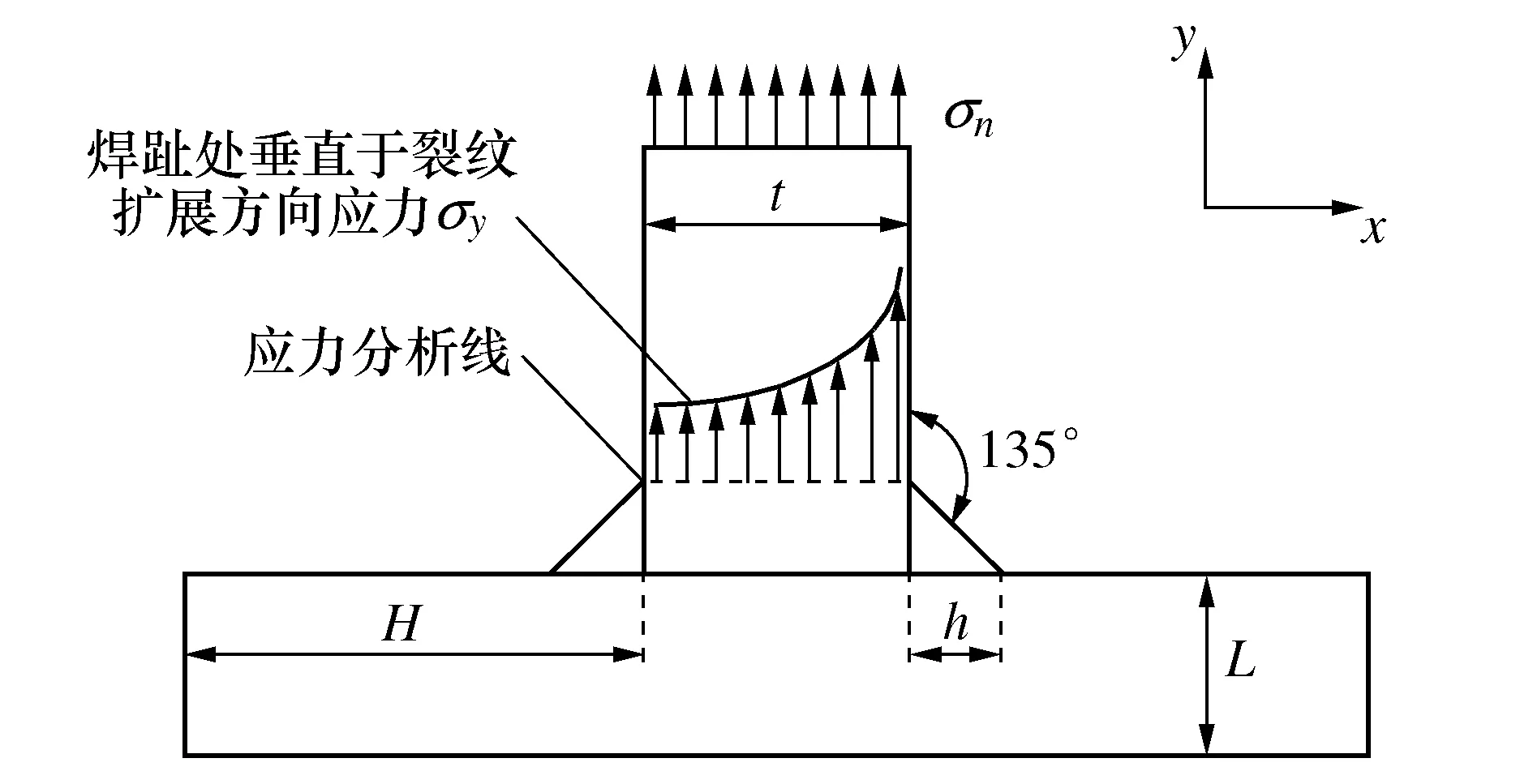
图2 受分析的结构边缘

通过上述计算,得到切口应力等效取值点xas和奇异强度as,即可计算出切口等效应力。

2.3 切口应力等效取值法考虑结构应力奇异性因素的验证

将切口等效应力计算公式中考虑应力集中的影响因子去掉,预测疲劳寿命,并与完整切口应力等效取值法和等效结构应力法预测的疲劳寿命进行对比。

1) 等效结构应力法预测寿命

按照图3的结构尺寸,采用Hypermesh17.0软件进行有限元建模,材料为16Mn钢,板厚为8 mm,采用八节点六面体单元和六节点五面体单元混合建模的方式,单元尺寸为2 mm,有限元网格数量为13 152个,节点数为16 626个,如图4所示。

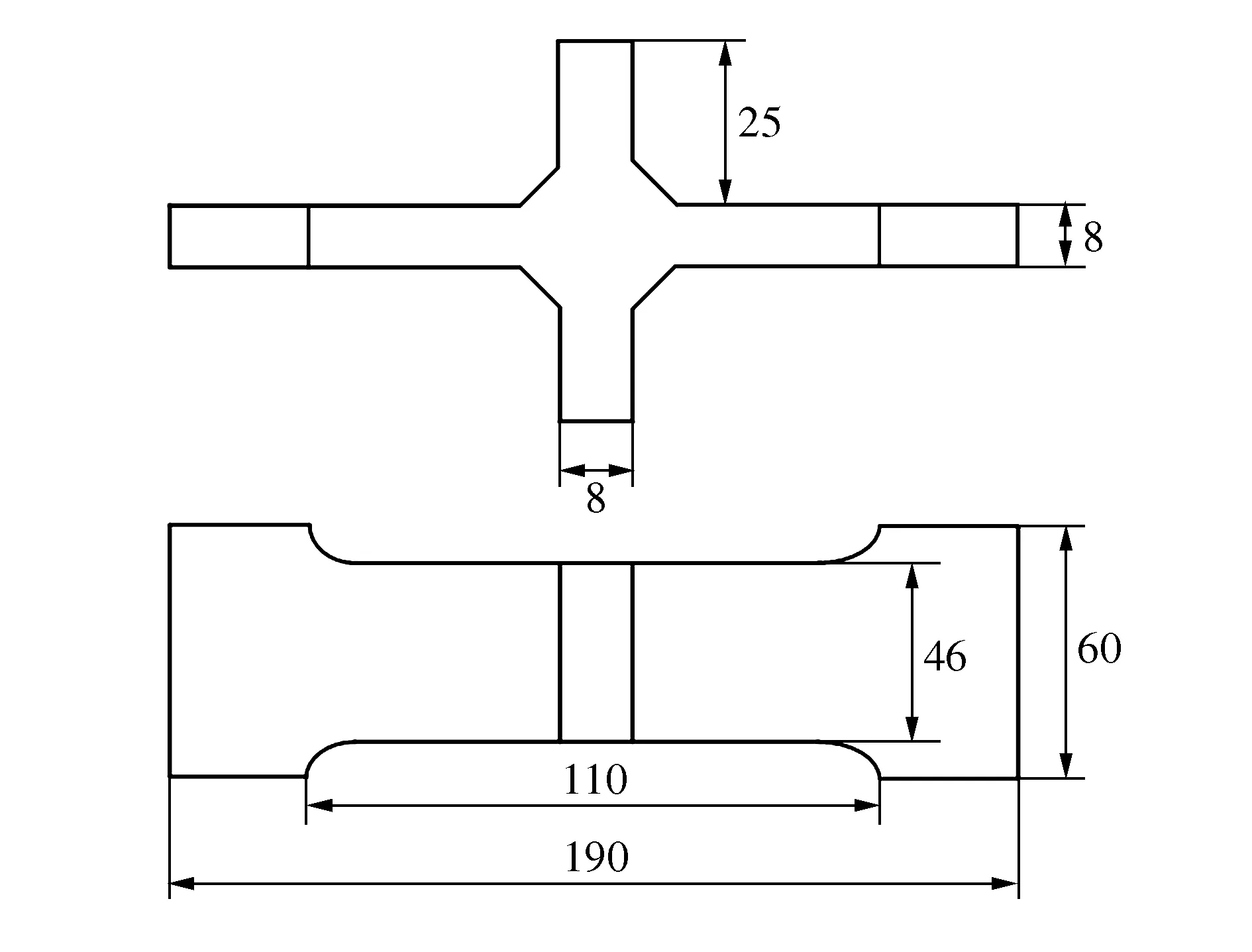
图3 十字焊接接头

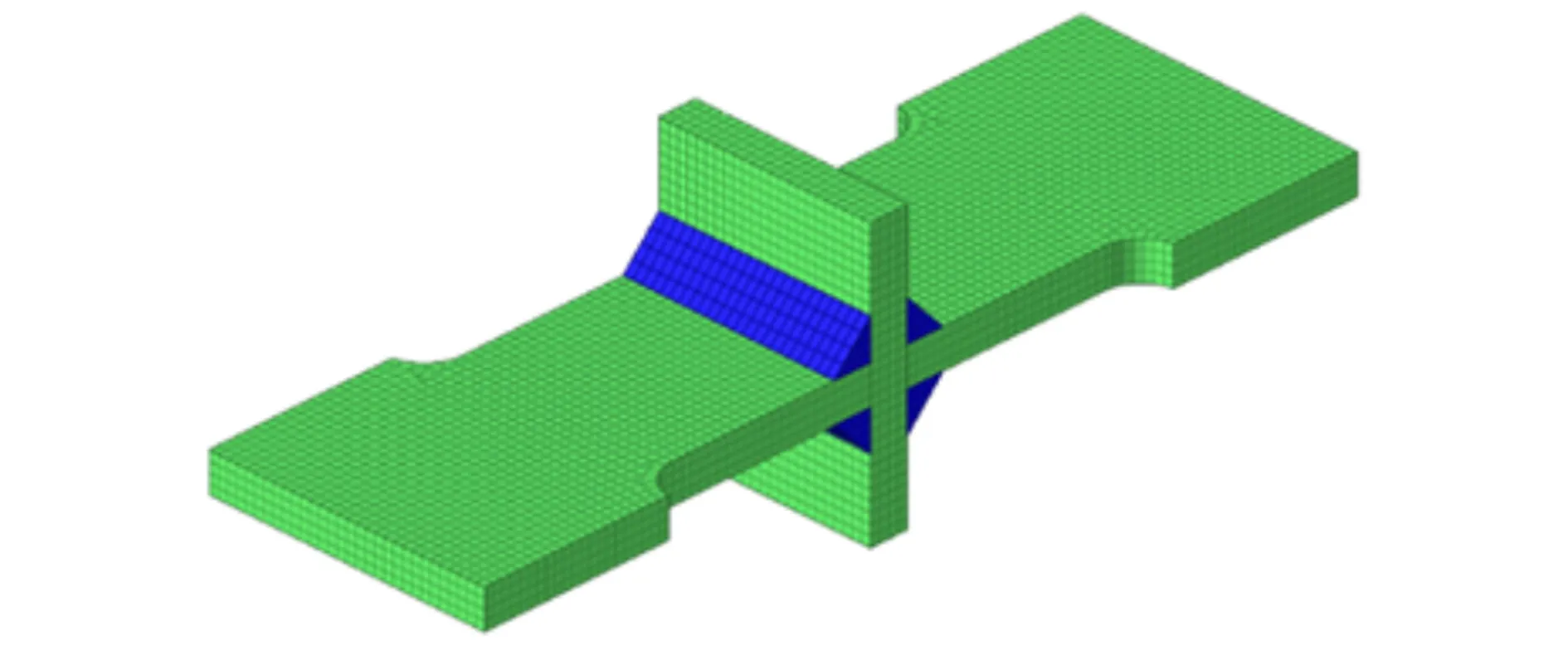
图4 十字焊接接头有限元模型

在十字焊接接头的一侧施加全约束,另一侧分别施加125 MPa、135 MPa、145 MPa、155 MPa、165 MPa、175 MPa应力水平的应力,并且按照Fe-weld软件中规定的格式建立焊缝,通过ANSYS软件进行仿真结果分析,最后应用Fe-weld软件计算出定义的焊缝位置的等效结构应力,通过-2σ主S-N曲线可计算出疲劳寿命,计算结果如图5所示。

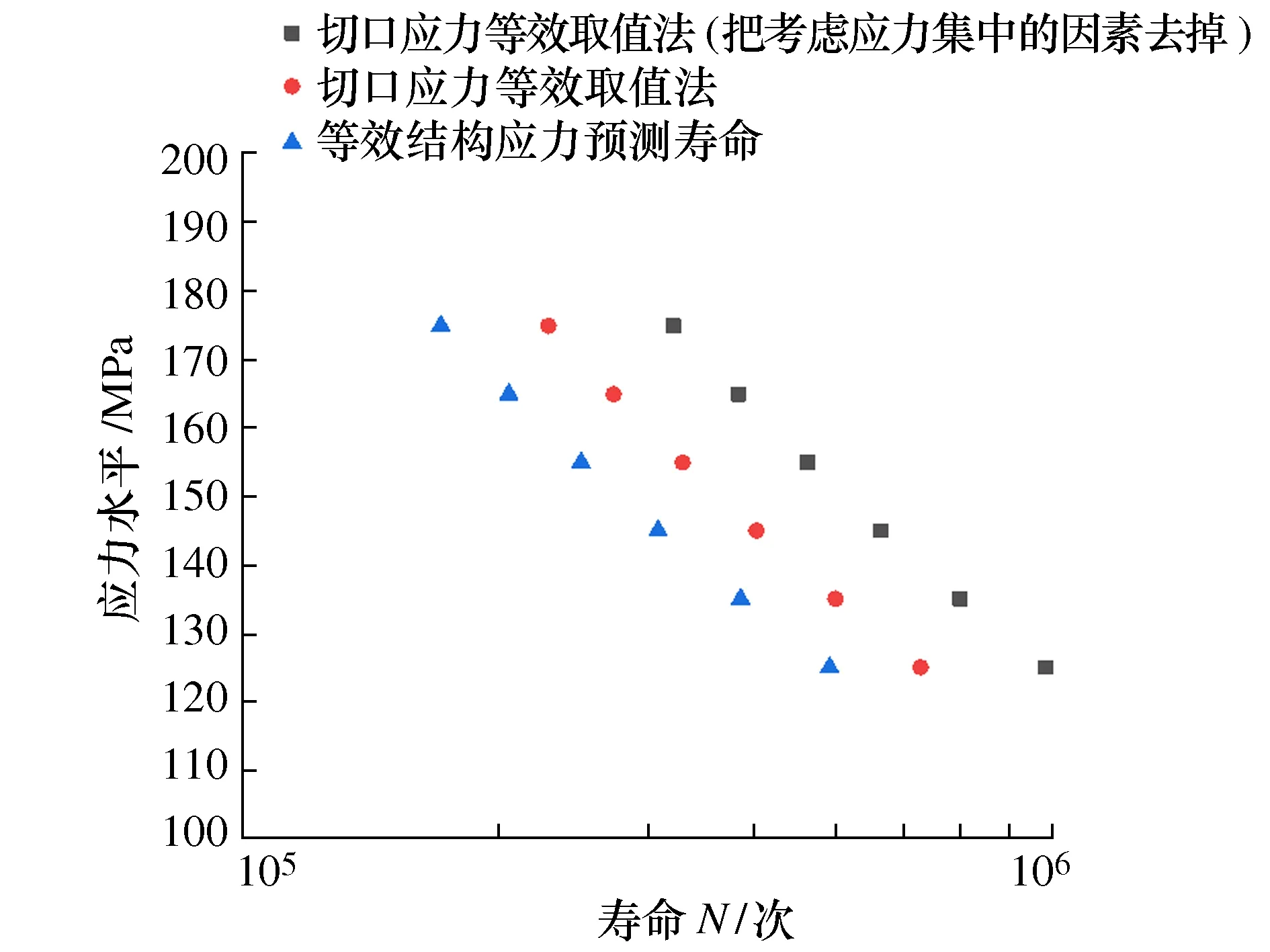
图5 3种预测结果对比

2) 切口应力等效取值法预测寿命

由图5可知,非受载板厚L=8 mm,非受载板高H=25 mm,受载板厚t=8 mm,焊脚尺寸h=8 mm。代入公式(7)可计算出奇异强度as=1.49 mm。根据奇异强度as的大小,可在表2切口应力等效取值点分段函数式参数中选取合适的参数,代入式(6),可计算出切口应力等效取值点xas=0.71 mm,将奇异强度as和切口应力等效取值点xas代入到式(3),即可计算出切口等效应力,如表3所示。根据焊接接头的形式,在BS标准中选取合适的接头等级,结合切口等效应力,可计算出预测疲劳寿命。

表3 不同应力水平下的切口等效应力

3) 切口应力等效取值法(将考虑应力集中的因素去掉)预测寿命

将切口等效应力计算公式中考虑应力集中的参数(即as)去掉,结合BS标准预测疲劳寿命。计算结果如图5所示。

由图5可知,相比切口应力等效取值法预测的寿命,把切口应力等效取值法中考虑应力集中因素去掉之后,预测的寿命与等效结构应力法预测的寿命相差更大。所以,可以证明切口应力等效取值法考虑了应力集中因素的影响。

3 实验结果与预测结果分析

3.1 疲劳寿命预测

采用SolidWorks对十字接头进行建模,几何形状如图3所示,材料为16Mn钢,可知非受载板厚L=8 mm,非受载板高H=25 mm,受载板厚t=8 mm,焊脚尺寸h=8 mm。采用与文献[15]和文献[16]相同的约束以及加载方式,通过切口应力等效取值法计算出切口等效应力,应用英国BS7608疲劳评估标准进行疲劳寿命评估,具体计算流程同2.3节所述一致。不同应力水平下的切口等效应力和预测寿命如表4所示。

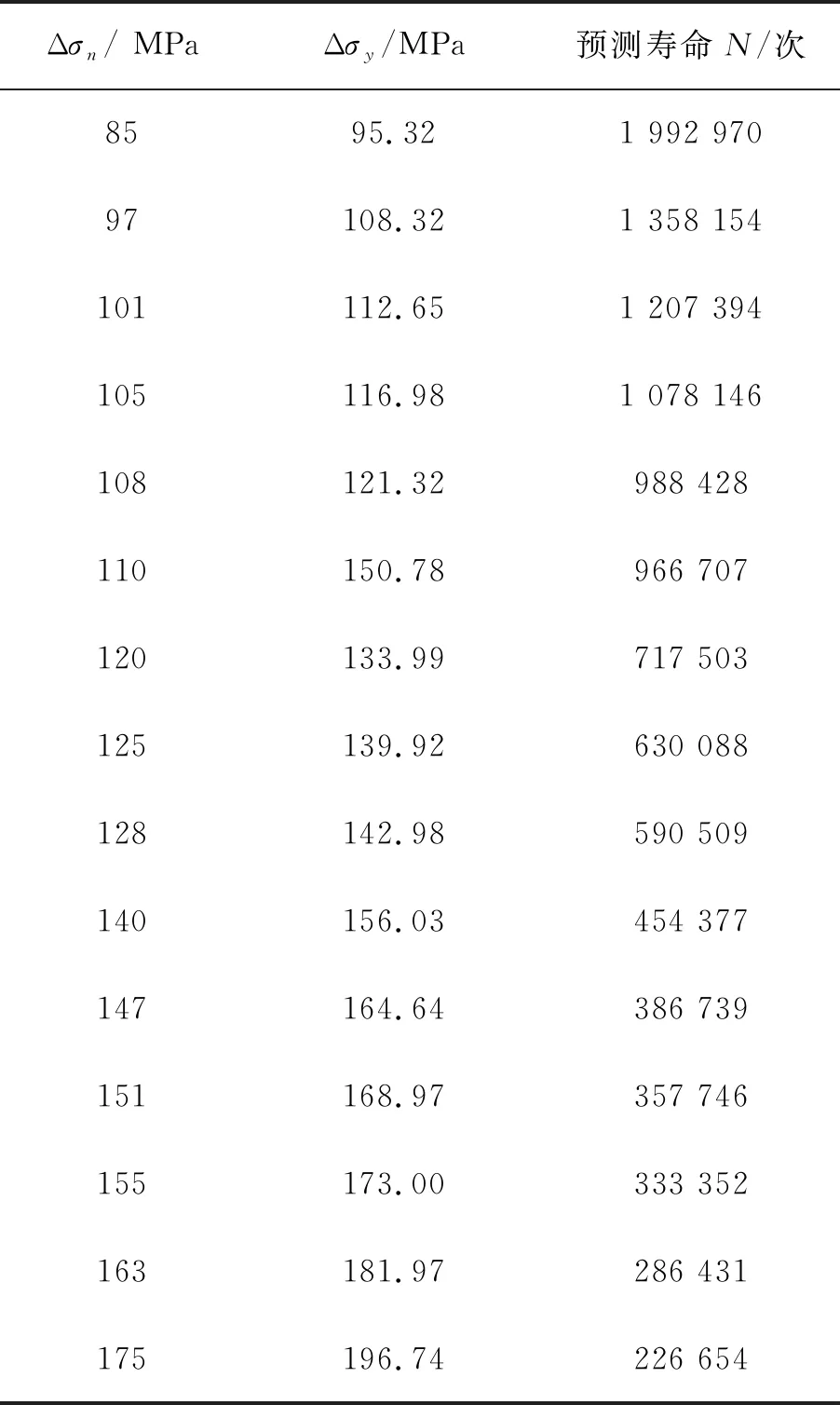
表4 不同应力水平下的切口等效应力和预测寿命

3.2 试验结果与预测结果对比

16Mn材料试验结果见文献[15],与预测结果对比如图6所示。在图6中可以看出,由于16Mn钢的焊接性能相对较好,以及采用了英国BS7608标准进行疲劳评估,所以通过切口应力等效取值法预测的16Mn钢十字接头疲劳寿命过于保守。接下来引入修正系数对切口等效应力的计算公式进行修正。

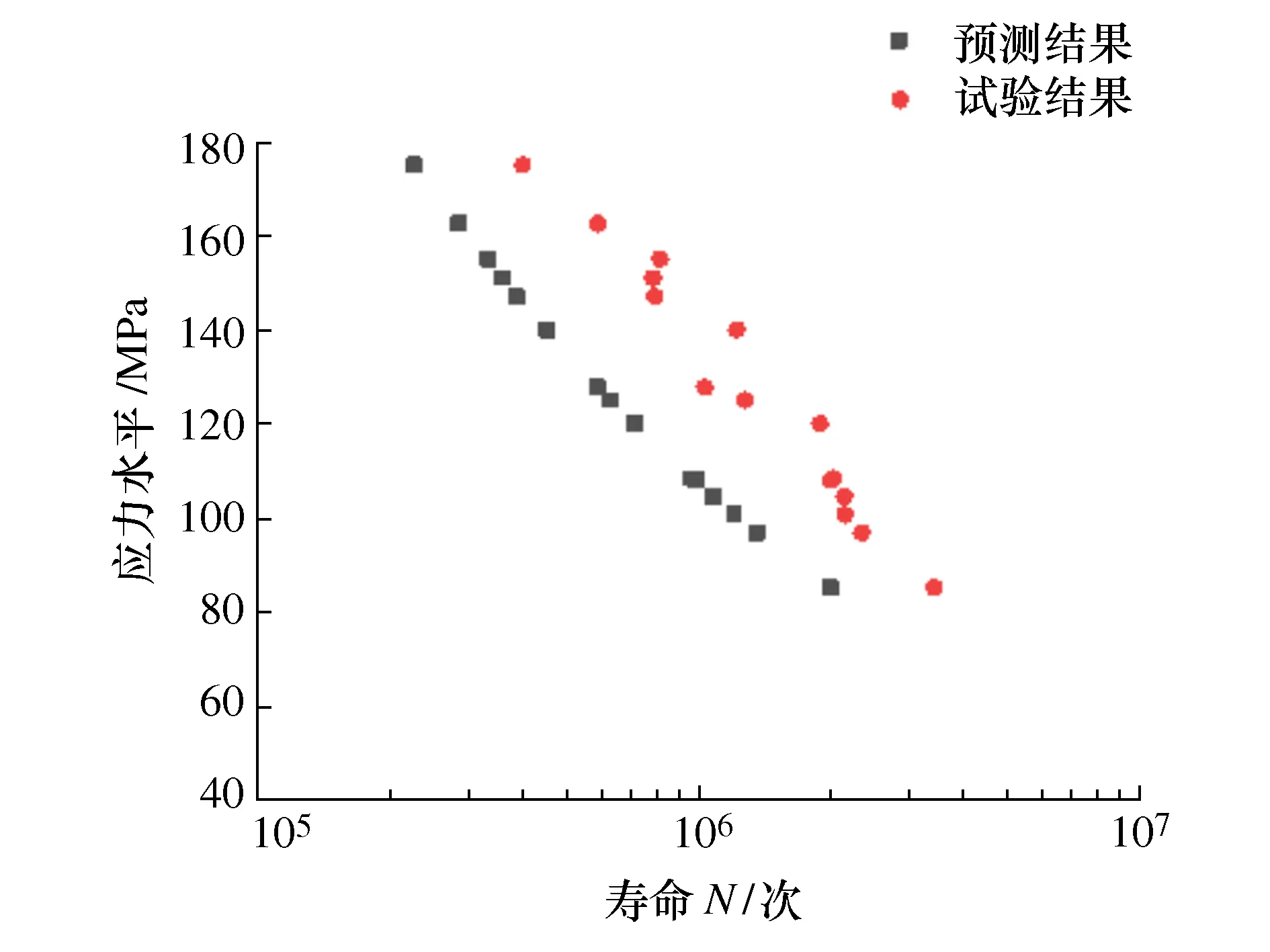
图6 试验结果与预测结果对比

3.3 切口等效应力计算公式的修正

引入修正切口等效应力概念σas,计算公式为

σas=fas·σy

(8)

式中fas为考虑16Mn钢的焊接性能对疲劳强度产生的影响而引入的修正系数。

疲劳寿命计算式为

(9)

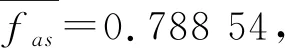
(10)

3.4 修正切口应力等效取值法的验证

1) 现有十字焊接接头的结构尺寸如图7所示,其材料为16Mn钢,施加载荷以及约束方式同文献[17]一致,文献[17]分析了超声冲击装置对焊接接头的疲劳强度的影响,参考其未进行超声冲击的焊接接头的试验疲劳寿命,来验证修正切口应力等效取值法的准确性。

由图7可知,非受载板厚L=8 mm,非受载板厚H=20 mm,受载板厚t=8 mm,焊脚尺寸h=4 mm。应用修正切口应力等效取值法计算出疲劳寿命为289 418周次,文献[17]中相同载荷以及约束条件下,试验寿命为298 000周次,误差仅为2.88%。

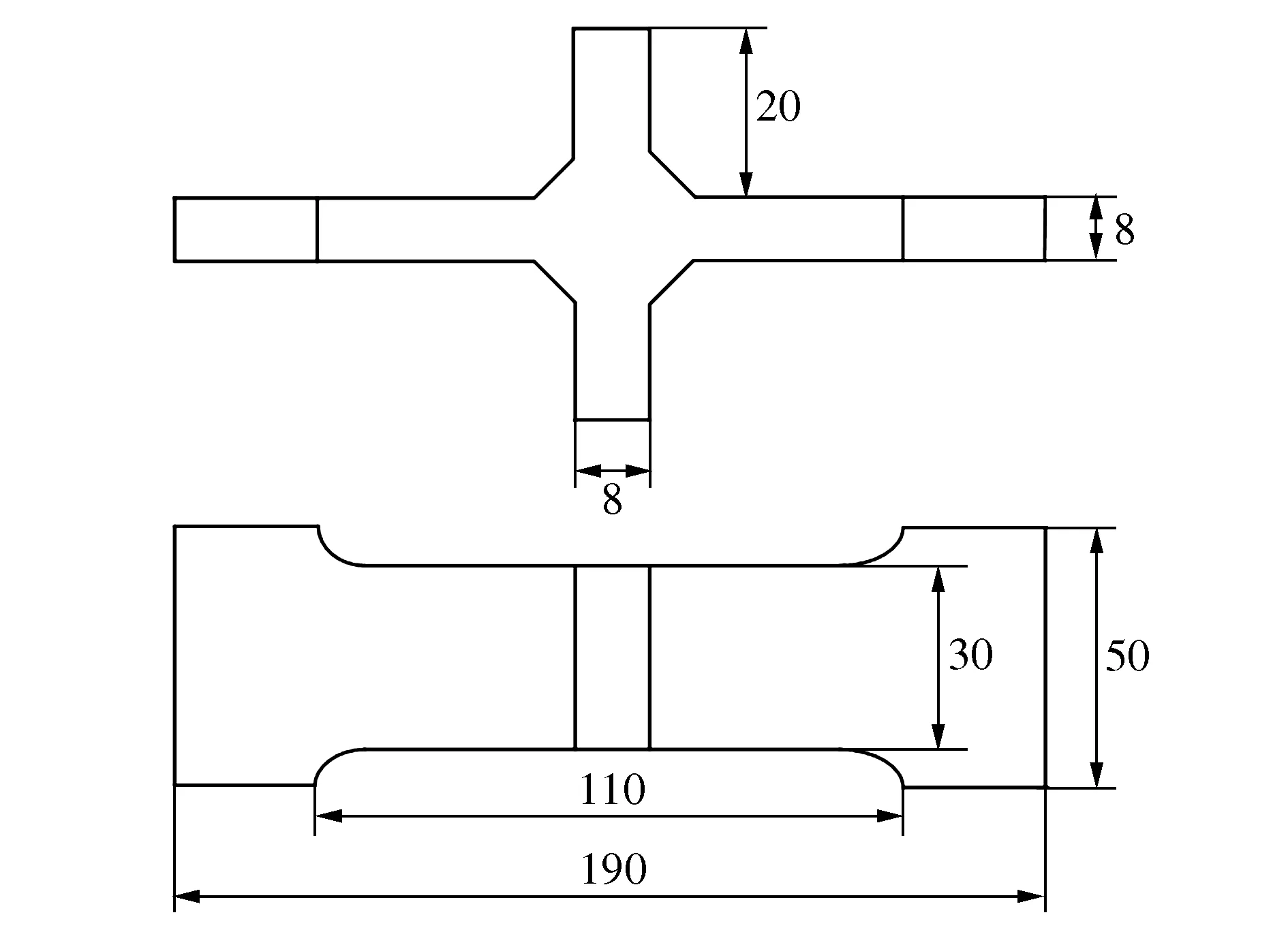
图7 验证1)所用接头结构尺寸

2) 现有焊接接头的结构尺寸如图8所示,其材料为16Mn钢,施加载荷以及约束方式同文献[18]一致,文献[18]分析了变幅载荷下TIG修整和超声喷丸处理的焊接接头的疲劳行为,参考其未进行变振幅负荷处理的焊接接头的试验疲劳寿命,来验证修正切口应力等效取值法的准确性。

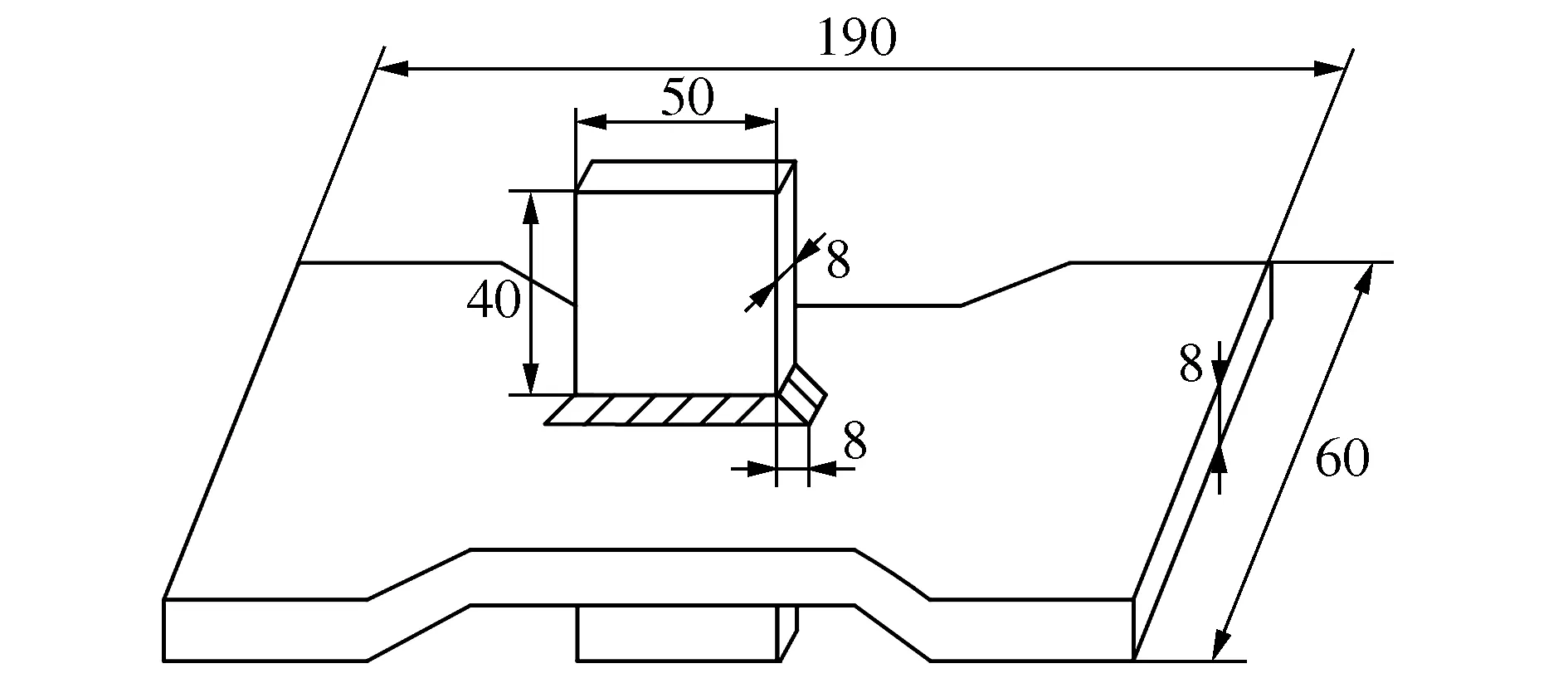
图8 验证2)所用接头结构尺寸

由图8知,非受载板厚L=50 mm,非受载板厚H=40 mm,受载板厚t=8 mm,焊脚尺寸h=8 mm。应用修正切口应力等效取值法计算出的疲劳寿命以及相同载荷和约束条件下的试验寿命如图9所示,可以看出,最大误差仅为5.96%。

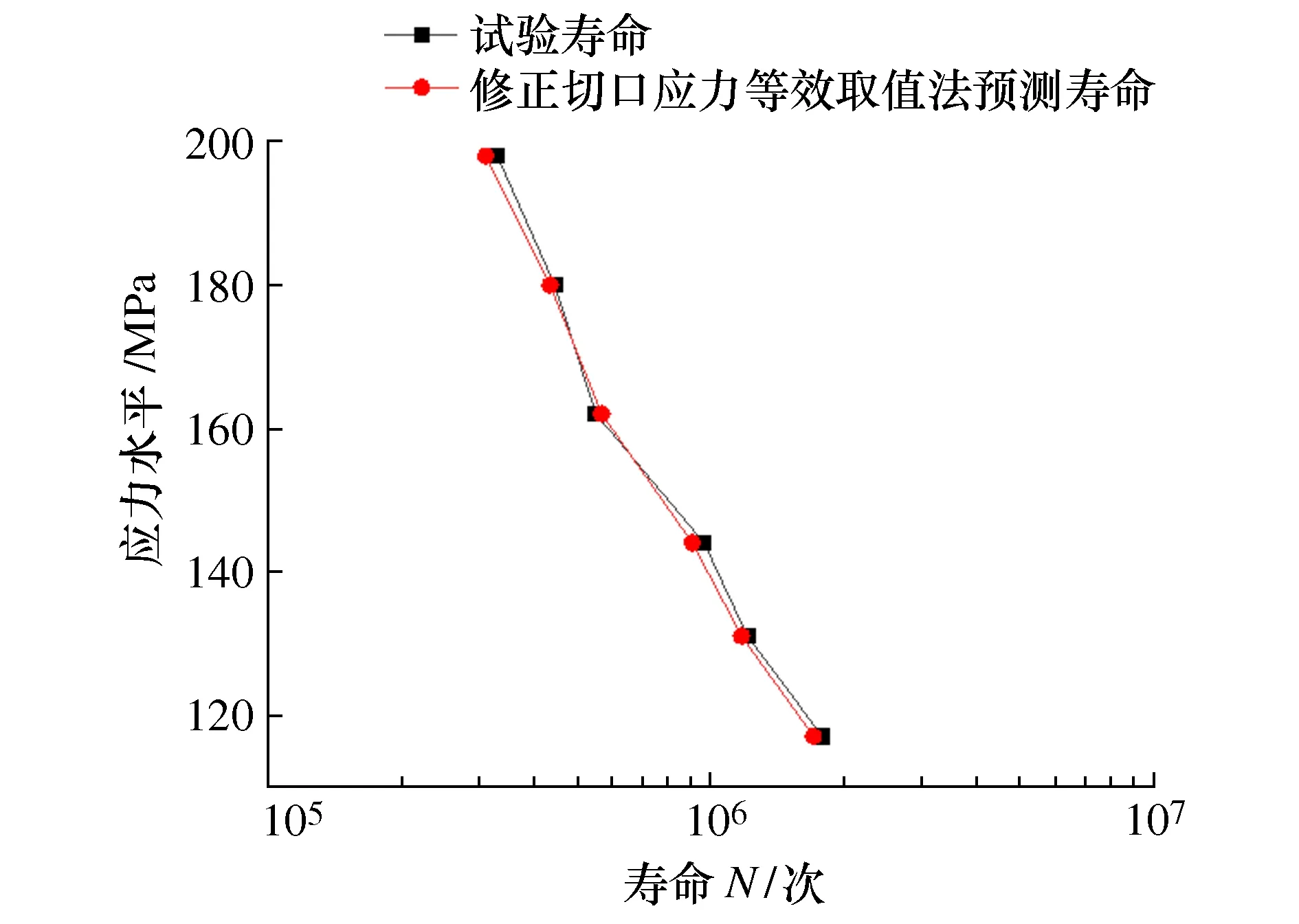
图9 验证2)试验结果与预测结果对比

从上述两个验证实例可以明显看出,修正切口应力等效取值法预测的疲劳寿命与真实试验寿命基本相同,有力地验证了修正切口应力等效取值法的有效性。

4 结论

1) 切口应力等效取值法和等效结构应力法均考虑了应力集中因素的影响,应用切口应力等效取值法预测16Mn钢寿命时,由于没有考虑材料焊接性能的影响以及应用BS标准(较保守)的原因,使得预测寿命存在一定的误差。

2) 修正切口应力等效取值法主要针对因结构的几何尺寸突变而导致的应力集中现象,可以准确计算出垂直于裂纹方向的应力分布,并通过切口应力等效取值点的计算,得到焊接接头切口等效应力的计算公式。

3) 引入修正系数,得到了适用于16Mn钢常用焊接接头切口等效应力的计算公式,并进行了验证。

4) 该方法为其它材料疲劳寿命的精准预测提供了可参考的方法。