考虑最优方向匹配的高效走刀轨迹生成方法

金鑫,刘其广*,,吕杰,徐飞飞

(1. 中国航发北京航空材料研究院,北京 100095; 2. 北京市先进运载系统结构透明件工程技术研究中心,北京 100095)

等残留高度轨迹在生成过程中保持了轨迹间最大加工行距,没有冗余切削,具有很高的加工效率[1-2],因而在学术界与工业界被广泛应用。然而,依据等残留高度原则排布的轨迹往往偏离最优走刀方向[3],而走刀方向对加工质量和效率有重要影响,如加工带宽[4-5],材料去除率[6],运动学性能[7],切削力[8-9],甚至流场方向[10]等。面向高性能切削需求,走刀方向与轨迹排布之间的矛盾亟需解决。

考虑加工中的走刀方向是将加工中几何、物理等特性融合在统一的刀具轨迹规划框架下的有效途径[11];为遵循最大加工带宽方向场, Chiou等[4]采用逐点追踪的方式生成轨迹,该方法只关注了局部方向最优,而没有从全局角度去考虑轨迹的光顺性。Kim 等[7]使用Bezier 多项式整体逼近离散方向场,改善了生成路径的光顺性。Sun等[5,12]采用NURBS矢量建模技术, 进一步提高了发生矢量场的局部调控能力,有利于加工轨迹的精细设计。尽管文献[5,7,12]中单条轨迹具有良好的切削性能,但相邻轨迹间往往存在冗余切削,造成加工效率低下。李万军等[13]使用遗传算法优化了刀具路径,缩短了轨迹总长度,但他们的方法中并没有考虑刀具进给方向的影响。

Xu 等[6]采用等残留高度原则排布轨迹,通过比较新生成的轨迹与按照理想方向切削带来的切削耗能方面的差别,提出该差异超出允许阈值时,则在未加工区域重新选择初始轨迹并继续等残留高度偏置,直至加工轨迹布满整个曲面。该方法在轨迹生成的同时,完成了曲面分割,显著改善了轨迹与最优方向的重合度。Kumazawa等[14]和 Liu 等[15]分析了球头刀加工复杂曲面的最优方向场,提出使用张量理论对曲面进行分割。在不同加工区域内的离散方向具有较好的一致性,因而按照等残留高度原则偏置轨迹时,可以限制其与最优方向的偏差。由上述分析可见,曲面划分可以调和等残留高度排布与加工方向之间的矛盾。然而,不同分割区域之间的接刀痕问题会显著影响加工质量。此外,因区域分割而导致的频起落刀亦会降低机床的加工效率。

将曲面视为一个整体的走刀轨迹规划依旧是学术研究中的热点。多数文献将走刀方向与轨迹排布问题分开讨论, 然而因等残留高度偏置而导致的轨迹偏离最优走刀方向的问题,尚未得到充分解决。基于此现状,本文提出了一种基于最优方向匹配的高效走刀轨迹生成方法,通过优化限定行距范围内的轨迹形状,以提高轨迹与最优走刀方向的匹配度。算例分析表明,该方法可在保持大行距排布的情况下,最小化轨迹切向与理想走刀方向偏差,继而显著提升机床的切削性能。

1 曲面上最优方向的确

曲面上任一点的进给方向定义在其切平面上,即

f=Sudu+Svdv

(1)

式中[du,dv]是该方向在参数域上对应的表达。

根据曲面与参数域的映射关系,可得

(2)

式中:E=Su·Su,F=Su·Sv,G=Sv·Sv,为曲面第一基本表达式的系数。

走刀方向关乎多种加工指标,如:加工带宽、材料去除率、机床运动学性能、切削力。根据加工需求,选定某种评价指标。考虑到进给方向与选定加工指标的关系往往高度非线性,可通过固定间隔采样等方式评价不同角度下的加工结果,进而优选出如图1所示的最优方向。为快速计算曲面上任意一点处的理想走刀方向。可先通过沿着u,v方向均匀采样,确定出采样栅格结点处的最优方向,然后判定目标位置所处栅格,利用如下双线性插值的方法,计算得到走刀方向。

图1 单点处最优方向选择

该插值示意可见图2,其具体计算过程为

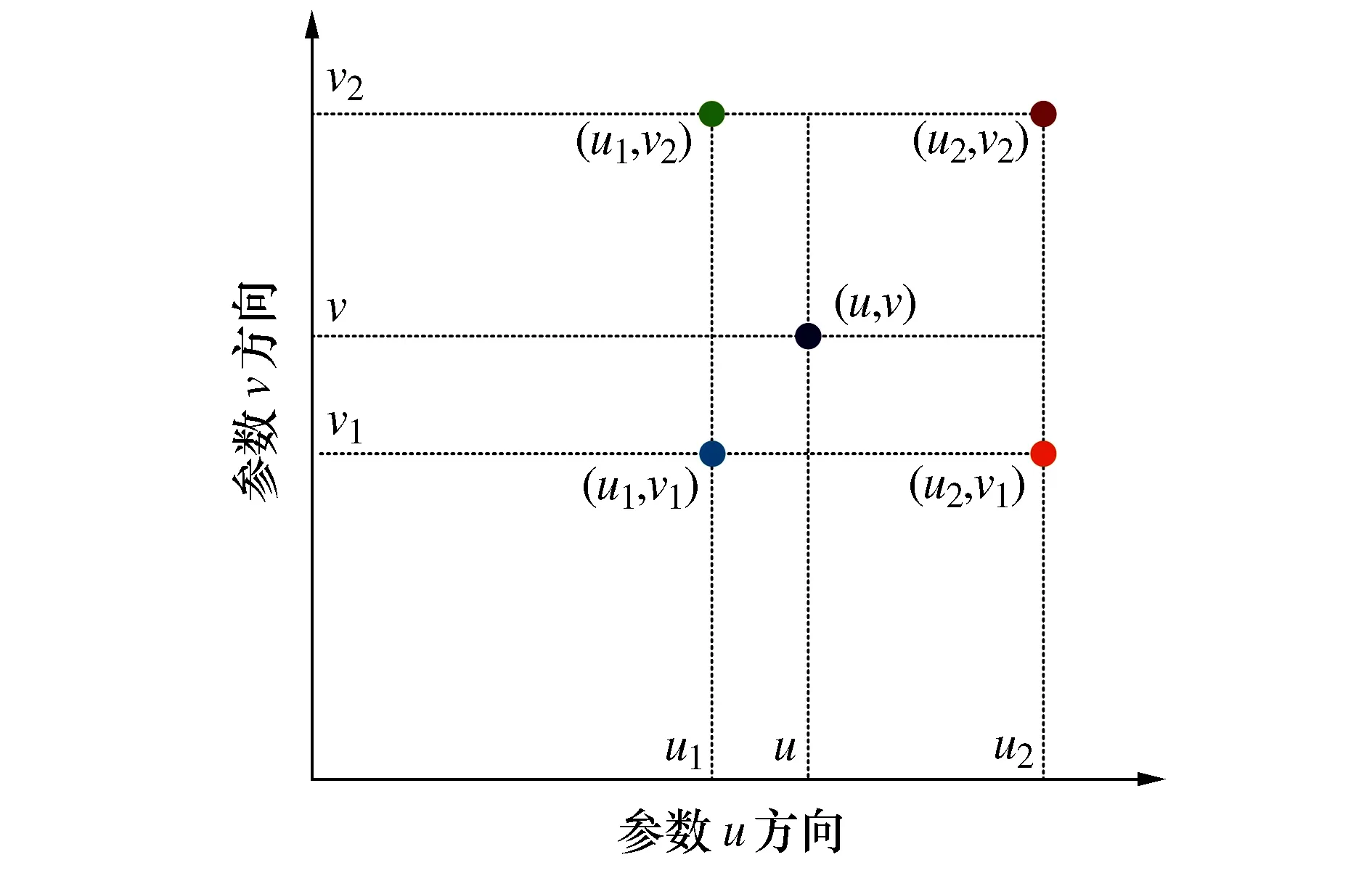
图2 参数域上的双线性插值

(v2-v)+f(u2,v1)(u-u1)(v2-v)+f(u1,v2)×

(u2-u)(v-v1)+f(u2,v2)(u1-u)(v1-v)]

(3)

式中f(ui,vj)是位置(ui,vj)处的最优方向,记为该方向与u/v线的夹角。

2 兼顾方向匹配与走刀行距的高效走刀路径

轨迹生成包含单条轨迹走刀样式的确定与不同轨迹间的排布方式。如前所述,按照等残留高度原则排布的路径有很高的加工效率,但却容易导致轨迹与最优方向的偏离。本节将通过在限定行距范围内优化轨迹形状,以兼顾最优方向匹配与大的走刀行距的要求。

2.1 轨迹排布的等残留高度原则

采用球头刀加工复杂曲面,选定曲面上的某条路径为当前轨迹,则轨迹上任一点的加工行距满足

(4)

式中:h为给定的残留高度;r为球头刀半径;R为曲率半径。

(5)

式中:L,M,N为曲面第二基本形式的系数,L=Suu·n,M=Suv·n,N=Svv·n,n为曲面上单位法向量;式(4)中的‘-’和‘+’对应‘Ldu2+2Mdudv+Ndv2’结果的正和负。

图3是轨迹的等残留高度原则偏置。

图3 轨迹的等残留高度原则偏置

如图3所示,当前点对应的下一条轨迹上的偏置点满足如下参数增量时,两点之间即符合等残留高度原则。

(6)

式中:b为行距方向的单位向量,可由单位法向量n与该点的单位进给向量f按照右手法则确定。对当前轨迹上所有刀位点进行上述操作,即可得到等残留高度轨迹。

2.2 行距限制下的方向匹配度优化

等残留高度轨迹在生成过程中确定了轨迹的形式,继而导致了与理想方向的偏离。为优化轨迹与方向的匹配度,引入系数γ(0<γ<1)以松弛轨迹排布中的等残留高度限制。如图4所示,在当前轨迹偏置生成下一条轨迹时,分别以行距w和γw作为偏置距离,得到边界轨迹。可知,在边界轨迹所确定区间上的任意一条轨迹都满足加工的残高要求。通过在该区间优化轨迹形状,即可实现提高方向匹配度的目标。松弛系数γ对优化效果有很大影响,为保证大的加工行距,并同时保证轨迹有足够的优化区间,γ∈[0.8,0.95]。

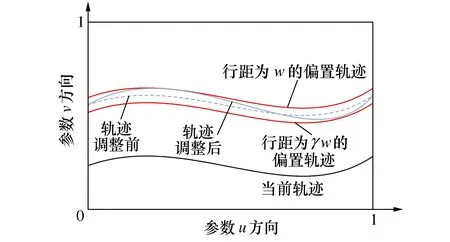
图4 偏置生成优化区间

采用B样条多项式表达目标轨迹和轨迹边界在参数域上的形式。所建立的优化模型为:

(7)

θi=arccos(dudui+dvdvi)

(8)

式中:(du,dv)是(ui,vi)处的理想方向;(dui,dvi)是该点处的实际单位走刀方向。

(9)

该优化模型的限制条件满足线性约束,但目标函数却存在非线性耦合。因此,采用成熟的遗传算法求解该模型。

3 算例验证

测试对象来源于模锻行业中常见的复杂曲面,采用r=8 mm的球头刀,加工残留高度h=0.05 mm,优化模型中的系数γ=0.9。尽管走刀方向对多种加工指标有影响,为方便采样,这里仅以最大加工带宽为目标构建离散方向场,如图5所示,采样栅格为21×21。在此基础上,本节采用数值仿真的方式规划了3种刀具轨迹(图6),并对它们进行了方向偏差分析(图7)和加工仿真验证(图8)。

图5 栅格采样和离散方向场构建

图6 3种方法规划的轨迹

图7 3种方法的轨迹在不同刀位处的方向偏差

图8 3种轨迹的仿真加工结果

轨迹生成的初始路径通过最优方向追踪选取,因为测试曲面具有中心对称性,可从中心位置通过前后搜索,得到初始轨迹。在此基础上,使用所提方法和等残留高度方法,分别生成测试曲面的加工路径,如图6a)和图6b)所示,将这两种路径分别记作dir_cusp_path和inio_cusp_path。为凸显方向对于加工效果的影响,同样采用等残留高度方法,以u=0.5的等参数线为初始轨迹,生成如图6c)所示的第三种路径并记作iniu_cusp_path。

按照加工步长误差对路径进行离散[16](步长误差设定为0.01 mm)。计算每种路径上方向匹配度,得到不同刀位点处的方向偏差如图7所示。每种路径的数据统计结果及路径长度信息汇总于表1。分析可知,就方向匹配度而言,所提方法生成的轨迹(dir_cusp-path)无论从最大值,平均值,中位数或者均方差角度评估,都有最好的表现;图6b)所示的轨迹(inio_cusp_path)次之;而图6c)所示的轨迹(iniu_cusp_path)最差。这表明所提方法可以显著提高生成轨迹与理想走刀方向的匹配度。

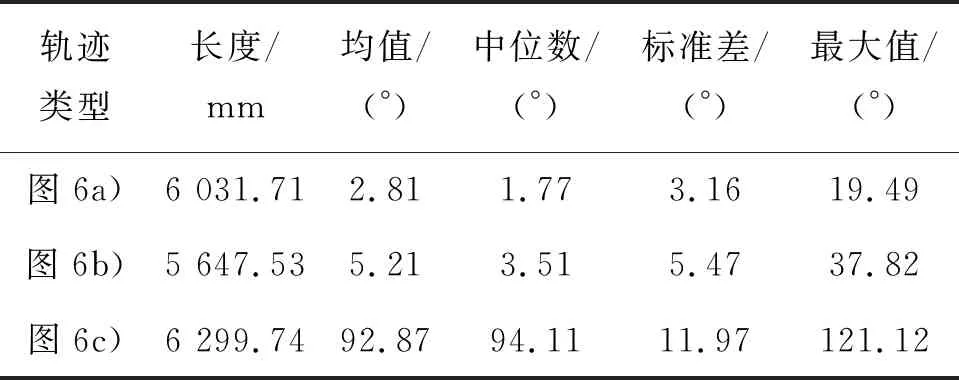
表1 轨迹信息汇总表

从路径长度上分析,inio_cusp_path占优,dir_cusp_path次之,而iniu_cusp_path依然最差,但这并不代表所提方法的轨迹效率低,由2.2节可知,方向匹配度的提升是以一部分加工行距为代价。事实上,dir_cusp_path仅比inio_cusp_path长6.8%,而平均最优方向的匹配度却提升了将近47.6%。这意味着如果选定的方向场与其他加工指标有关,可以通过牺牲少许效率换取某项加工指标的提升。此外,dir_cusp_path长度短于同是按照等残留高度原则生成的iniu_cusp_path。这表明轨迹的加工效率与走刀方向有关,而遵循最优加工带宽的轨迹,即使不是按照等残留高度原则排布,加工效率也有可能高于某些初始轨迹条件下的等残留高度路径。

最后,使用Vericut对3种轨迹进行加工仿真,仿真结果如图8所示,其中图8a)～图8c)分别表示dir_cusp_path、inio_cusp_path和iniu_cusp_path的仿真加工结果。 图8c)所示结果有部分超差,但是区域零碎,在可接受范围以内;图8a)和图8b)所示的加工残留均不大于设定值h=0.05 mm,表明了所提方法的合理性和有效性。

4 结论

1) 依据离散方向场,提出了曲面上任意一点最优方向的快速计算方法。

2) 通过引入系数γ,可以保证在大的加工行距下,限定轨迹调整的区间。

3) 通过将理想方向与轨迹在切向的偏差角定义为方向匹配度,构建了最小化偏差角的优化模型。

4) 所提方法可通过遗传模型求解。优化后的轨迹在保证加工精度的前提下,不仅可以保持高的加工效率,并可显著提升走刀方向的匹配度。