卡尔曼滤波框架下优化增益异类噪声处理方法及其应用*
赵 岩,王 宁,韦道知
(空军工程大学 防空反导学院, 陕西 西安 710051)
状态估计是从已有信息中提取有用信息[1],并对系统模型的某些参数进行校正的方法。状态估值的精度和可靠性与系统模型是否准确描述直接相关[2]。实际系统的非线性模型可以有效还原系统的真实性,但过于复杂的模型,计算大,甚至难以计算[3]。因此,系统模型应对实际系统进行适当简化,降低系统的非线性程度。与此同时,系统不可避免地引入了一定干扰。
目前,常用的非线性系统状态估计方法有无迹卡尔曼滤波(Unscented Kalman Filtering, UKF)方法、粒子滤波(Particle Filtering, PF)方法以及相关改进方法。UKF通过Unscented变换,获得状态一步预测的一阶、二阶统计信息,能够对较高非线性度系统进行有效估计,估值精度达到二阶以上[4]。但UKF方法对初始噪声相对敏感,不准确的初始误差模型会严重影响UKF方法的滤波性能[5-7]。PF方法能够处理强非线性系统[8],PF方法利用蒙特卡洛方法,随机产生一组含有权值的粒子,近似状态的后验概率分布。但PF方法也会面临粒子匮乏等问题,导致状态估值陷入局部最优。这些非线性方法都存在计算量大、实时性相对较差的缺陷。对于线性系统,卡尔曼滤波(Kalman Filtering, KF)算法无疑是最实用和成熟的方法,广泛应用于航空航天、工业控制、通信、经济金融等领域。为了在非线性系统中应用KF算法,通过改进得到扩展卡尔曼滤波(Extended Kalman Filtering, EKF)算法[9],该方法利用Taylor级数,将非线性系统线性化,然后进行KF算法迭代,能够获得非线性系统的状态估值。
除了系统模型,系统受到的干扰也是影响状态估值精度和可靠性的一个重要因素[10]。一般的方法是将干扰(包括系统内部和外部干扰)转换成随机高斯噪声(Stochastic Gaussian Noise, SGN)的形式。但实际系统的干扰往往相当复杂[11],单一的SGN并不能较好地模拟系统干扰。受技术条件限制,早期滤波难以处理非高斯噪声(Non-Gaussian Noise, NGN),但随着滤波技术的发展,产生了多种处理不同形式噪声的方法。
文献[12]研究了含有互相关噪声的多传感器系统,利用全局最优分布式算法对状态进行估计,并将设计方法应用到目标跟踪模型中进行仿真,验证了方法的估计效果。文献[13]利用滤波技术研究了含有自回归噪声的双线性系统的参数估计问题,根据辨识后的模型采用改进最小二乘迭代方法获得了有效估计值。文献[14]通过系统辨识处理含有未知有色噪声的双线性系统,再利用KF算法对系统参数进行估计,通过数字仿真证实了这种方法的有效性。文献[15]为了克服KF算法缺陷,采用最大相关熵准则对KF算法进行改进,并对非高斯噪声系统进行状态估计。文献[16]采用一种回归方法对未知统计特性的有界噪声系统进行参数估计。上述文献利用不同方法对线性和非线性系统的参数进行估计,都将干扰噪声按照同一形式进行处理,没有考虑系统噪声的异质性对滤波带来的影响。
综上,本文针对基于KF框架算法在处理NGN系统时的局限性,提出一种能够同时处理含有随机高斯噪声和未知有界噪声两种异类噪声的改进算法。该方法利用最小均方误差估计原则,在吸收集员估计处理未知有界噪声能力的基础上,调节卡尔曼滤波增益,使改进后的算法具有处理非高斯噪声的能力。
1 KF框架及对噪声的要求
1.1 KF框架
KF算法是针对线性系统状态的一种有效估计方法。通过赋予状态量和协方差矩阵初值,利用不断更新的观测量,获得下一时刻的状态估值。但采用标准KF算法计算系统准确的状态估值是有严格要求的。首先,系统是线性的,而在现实中,几乎不存在真正的线性系统。然后,系统模型精确已知,而实际建立的系统模型总存在不同程度的误差和干扰,很难给出准确的模型。另外,对系统噪声也有一定的要求。但是,KF算法是一种递推算法,特别适合计算机应用,被广泛应用于航空航天、工业控制、通信、经济金融等领域。
标准KF算法的计算流程如图1所示。KF框架是根据KF算法流程,利用状态量的一、二阶矩统计信息,代入观测信息后,通过状态方程和观测方程,实现时间更新和量测更新的过程。采用KF框架的滤波算法主要有KF算法、EKF算法及其改进算法。

图1 标准卡尔曼滤波算法流程Fig.1 Flow chart of the standard Kalman filtering algorithm
EKF算法是KF算法在非线性领域的推广。采用KF框架,通过将非线性模型进行Taylor展开,对二阶以上项(含二阶项)进行截断,获得状态矩阵和观测矩阵的Jacobian矩阵,然后再利用KF框架进行计算。虽然线性化过程产生了误差,但是解决了KF算法在非线性系统中的应用问题。对于非线性度较大的系统模型,采用EKF算法进行计算会导致状态估值发散。
1.2 基于KF框架的算法对系统噪声的要求
基于KF框架的滤波算法对系统的噪声有严格的要求。
当噪声是已知的高斯噪声时,基于KF框架的算法是一种递推最小均方误差(Mean Square Error, MSE)估计准则。当噪声分布为非高斯、且前二阶矩已知时,该估计器为最优线性估计器。但在实际情况中,系统噪声分布具有不确定性,且统计信息难以准确获得,因此很难满足对噪声的这一要求[17]。尽管基于KF框架的算法在实际应用的条件很苛刻,但适合计算机运算,且计算量相对较小。因此,将实际模型简化后,KF算法仍然是目前应用最为广泛的、获得次优状态估值的高效方法。
对于某一系统模型,采用基于KF框架的滤波算法进行解算时,系统的过程噪声Wk和观测噪声Vk应同时满足:
(1)
式中:Qk为系统噪声序列的方差阵,Rk为观测噪声序列的方差阵,且Qk与Rk相互独立;δkj为Kronecher函数。
2 集员滤波及未知有界噪声
如果系统噪声分布不能满足高斯分布,基于KF框架的滤波算法性能会显著下降,甚至发散。在实际应用中,大多数噪声是不满足这种假设的,有的噪声甚至难以用数学语言描述。
针对这类随机噪声,为了获得更加准确、可靠的系统状态估值,集员滤波(Set Membership Filtering, SMF)算法进入了研究人员的视野。SMF算法是一种在未知但有界(Unknown But Bounded, UBB)噪声假设下的估计方法,其估计目的是寻求所有与模型结构、观测数据和噪声有界假设相容的状态或参数组成的可行集合(Feasible Set, FS)[16]。通过该方法得到的估计结果不是一个准确值,而是一个集合,即可行集。状态参数可行集中每个元素都是系统有效的状态估值。一般将可行集的中心作为状态的点估计,可行集的测度作为衡量SMF算法有效性的标准。
2.1 集员滤波的系统噪声
如前,集员滤波器是将UBB噪声转换到椭球集合中,用椭球集合表示这些参数的可能分布。
定义1一个椭球集合可表示为:
E(a,P,σ)={x∈Rn:(x-a)T(P)-1(x-a)≤σ2}
(2)
式中:a为椭球E(a,P,σ)的中心;P表示椭球E(a,P,σ)的形状矩阵,且为正定矩阵;σ为椭球E(a,P,σ)半径。
对于系统的UBB过程噪声wk和观测噪声vk,用椭球集合可以表示为:
(3)
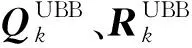
2.2 集员滤波框架
SMF算法分为时间更新和量测更新两步,如图2所示。时间更新即通过前一时刻状态椭球和由状态方程获得的椭球(含过程噪声椭球集合)进行Minkowski和计算,得到的状态一步预测椭球集合的过程。量测更新即把得到的状态一步预测椭球和观测方程椭球(含观测噪声椭球集合)进行交集计算,得到当前时刻状态椭球集合的过程。
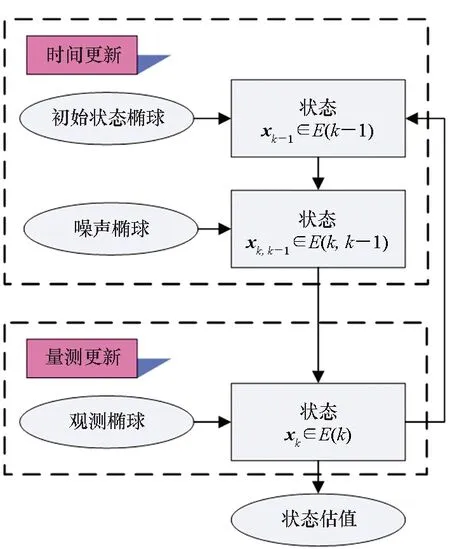
图2 集员滤波算法流程Fig.2 Flow chart of the set-membership filtering
状态xk-1属于椭球集合E(k-1),表示为:
(4)
状态一步预测xk,k-1的集合为:
xk,k-1∈Fk-1E(k-1)+Wk-1
(5)
式中,Fk为系统的状态矩阵,Wk-1为过程噪声椭球集合。
定义2两个椭球集合E(a1,P1,σ1)与E(a2,P2,σ2)的Minkowski和包含于的外定界椭球集合为:
E(a,P,σ)⊇E(a1,P1,σ1)+E(a2,P2,σ2)
(6)
式中:
其中:p的值需要根据选择最小化椭球集合的方法而定。常用的方法有最小容积椭球和最小迹椭球[18],但无论采用哪种最小化椭球的方式,σ2最终可被消除。式(6)可最终表示为:
E(a,P*,1)⊇E(a1,P1,σ1)+E(a2,P2,σ2)
(7)
式中:
(8)
椭球集合Fk-1E(k-1)和过程噪声椭球集合Wk-1的Minkowski和一般不为椭球集合,为使xk,k-1包含于一个标准的椭球集合,根据定义2,状态一步预测xk,k-1的集合为:
xk,k-1∈E(k,k-1)⊃Fk-1E(k-1)+Wk-1

(9)
观测椭球集合为:
(10)
式中,Hk为系统的观测矩阵,Vk观测噪声椭球集合。
量测更新椭球集合为:
xk∈E(k)=E(k,k-1)∩S(k)
(11)
定义3两个椭球集合E(a1,P1,σ1)与E(a2,P2,σ2)的交集包含于的外包界椭球集合为:
E(a,P,σ)=E(a1,P1,σ1)∩E(a2,P2,σ2)
(12)
式中:
根据式(12),式(11)可表示为:
(13)
3 基于KF框架的优化增益异类噪声处理方法
针对EKF算法在处理非线性系统时,受到系统模型准确性和高斯噪声模型已知的要求限制,设计一种基于KF框架的异类噪声处理方法。首先区分系统中的异类噪声,然后对滤波增益进行优化,最后给出改进算法。
3.1 异类噪声
模型是真实系统的高度抽象,建立与实际非线性系统一致的数学模型是极其困难的。即使能够根据物理特性构建系统的模型,但系统仍然会受到外界环境的未知干扰。其中有些干扰能够获得统计分布,而大多数干扰难以获得。加之非线性系统线性化的截断误差,使得EKF算法对非线性系统状态进行估计时,无法获得状态的最优估值。因此,将系统无法准确描述的线性化截断误差、外界未知干扰和系统噪声进行处理,转变成UBB噪声,与系统中可以描述的高斯噪声共同构成本文研究异类噪声的主体。因此对系统可能出现的异类噪声进行分类,如表1所示。

表1 系统异类噪声分类Tab.1 Classification of the system heterogeneous noise
3.2 滤波增益优化
通过调整滤波增益,使EKF算法能够同时处理这两类异类噪声。
引理1若存在矩阵A、B和X,则下列矩阵函数的迹对X求导的等式成立。
(14)
定理1若EKF算法的滤波增益Kk满足
(15)
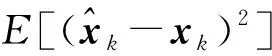
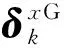
证明:
假设系统状态估值为:
(16)
类似地,假设观测量为:
(17)
则状态的MSE为:
(18)
存在
(19)
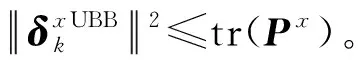
根据标准KF状态估值方程,得到:
(20)
计算MSE,并将式(20)代入,则:
(21)
再将式(17)代入式(21),可得:
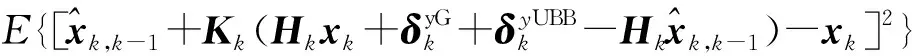
(22)
(23)
并将式(23)代入式(22),得到:
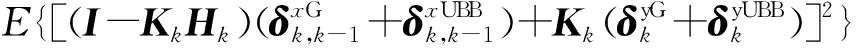
(24)

(25)
式(25)右边第三项利用式(7)可得:
⊂E(0,Pk(p),1)
(26)
根据式(8)可得:
(27)
因为
(28)
所以
(29)
根据式(18)和式(25)可知:
(30)
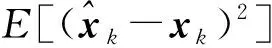
(31)

(32)
□
3.3 改进算法
综上,基于KF框架的优化增益异类噪声处理方法如式(33)所示。
(33)
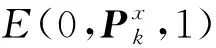
4 数字仿真实验
4.1 仿真系统模型
建立粗糙的车辆运动模型作为导航系统的状态方程。
xk=Fk-1xk-1+Wk-1
(34)

其中,sE,sN,vE,vN,aE,aN分别表示东向位置、北向位置、东向速度、北向速度、东向加速度和北向加速度,t为采样时间。
zk=hk(xk)+vk
(35)
其中:zk=[d,θ]T;d,θ分别为里程计输出的距离信息和方位陀螺输出的方位角信息;hk为非线性观测函数,其Hessian矩阵为Hk。
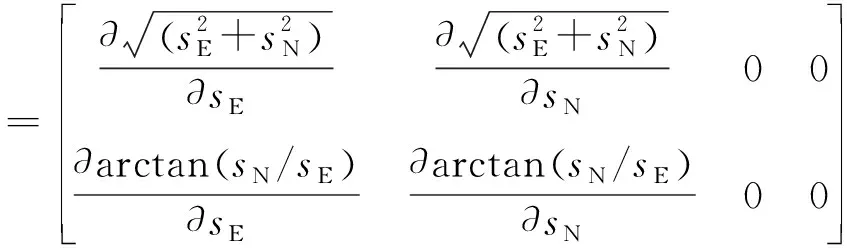

4.2 仿真结果分析
采用本文设计的滤波方法和EKF算法对4.1节中的车辆导航模型进行仿真,经处理得到东向、北向的位置和速度误差结果,如图3~8所示。
图3和图4为两种滤波算法对系统位置误差的估计曲线。由于前30个历元两种算法估值接近,为了更加清楚地比较位置误差估计结果,分别在图3和图4左下角绘制出前30个历元东向和北向的位置误差估计曲线。由图3和图4可知,EKF算法可将位置误差均值控制在15 m以内,且估计精度逐渐变差;本文算法具有较稳定的估计精度,能够使位置误差均值控制在4 m以内。造成这样的原因是里程计和陀螺仪传感器的误差积累使算法计算精度有所下降,而本文算法具有较好的克服系统误差的能力。
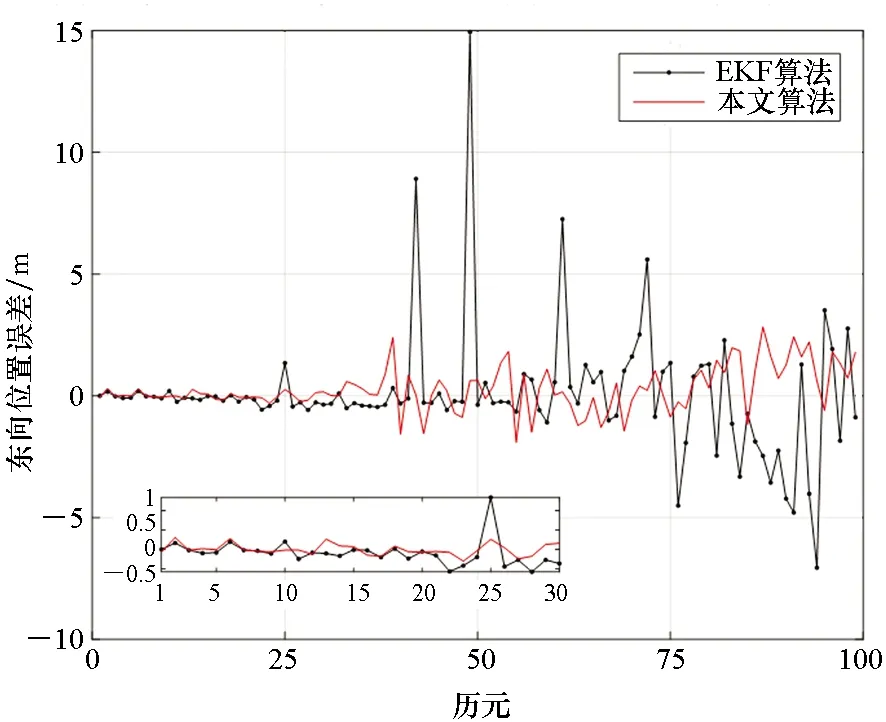
图3 东向位置误差曲线Fig.3 Eastern position error curves

图4 北向位置误差曲线Fig.4 Northern position error curves
图5和图6为两种滤波算法对系统速度误差的估计曲线。同样,分别在图5和图6左下角绘制出前30个历元东向和北向的速度误差估计曲线。由图5和图6可知,EKF算法可将速度误差均值控制在3 m/s以内,且估计精度逐渐变差;本文算法具有较稳定的估计精度,能够使速度误差均值控制在0.3 m/s以内。
图5和图8为50次蒙特卡洛的后输出的位置和速度的均方误差曲线,从图中可以看出,本文提出的基于异类噪声处理机制的KF算法精度优于EKF算法的计算精度。仿真得到的位置和速度误差的均值和标准差如表2所示。本文算法的状态估值均值和标准差均小于EKF算法的计算结果。EKF算法的计算时间为0.165 s,本文算法的计算时间为0.132 s。算法耗时是在Windows 10系统主频2.2 GHz处理器条件下,由MATLAB R2015a软件计算得到的。通过比较可以看出,两种算法的计算量相当,本文算法的计算时间略短于EKF算法。因此,本文算法的估计精度高于EKF算法,且具有更好的抗误差扰动能力,一定程度上能够提高车辆导航定位的精度。
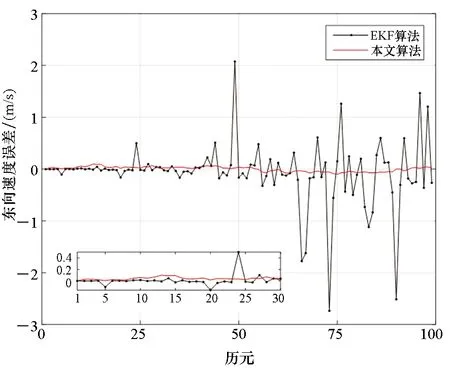
图5 东向速度误差曲线Fig.5 Eastern speed error curves
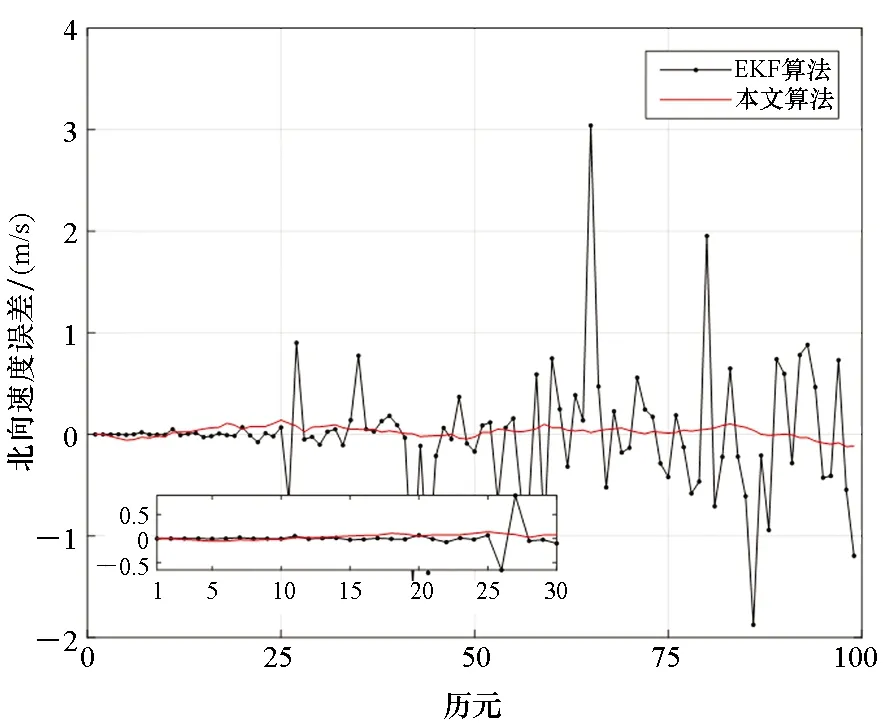
图6 北向速度误差曲线Fig.6 Northern speed error curves

图7 位置均方误差Fig.7 Position of the RMSE

图8 速度均方误差Fig.8 Speed of the RMSE
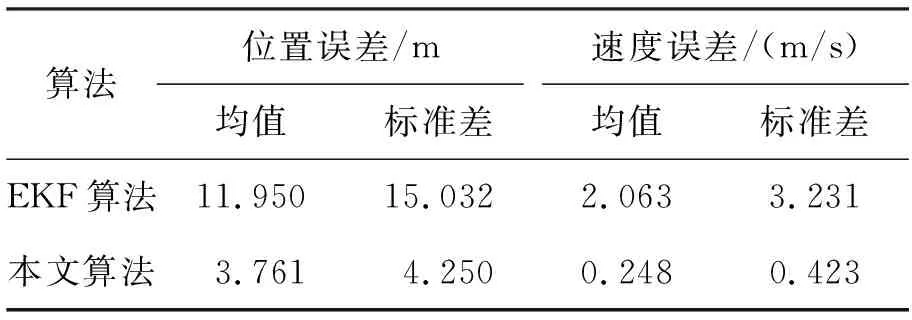
表2 水平位置误差比较Tab.2 Horizontal position error compare
5 结论
本文提出一种基于卡尔曼滤波框架的优化异类噪声处理算法,在吸收集员滤波处理UBB噪声优点的基础上,通过调整滤波增益使系统状态估值均方误差达到最小,且能够同时处理含有高斯噪声和未知有界噪声的系统。并将该算法和EKF算法应用到车辆导航系统模型中,在给定相同噪声的条件下,当UBB噪声上限相对较小时,通过数字仿真实验发现本文方法对系统噪声且具有更好的抗误差扰动能力。

