无奇点三维攻击时间控制滑模导引律*
常思江,吴 放,陈升富
(1. 南京理工大学 能源与动力工程学院, 江苏 南京 210094;2. 中国电子科技集团公司第二十研究所 雷达事业部, 陕西 西安 710068)
现代战争条件下,为了提高导弹的毁伤与生存能力,可通过对导弹的导引律增加一些终端约束予以实现。其中,增加攻击时间约束对导弹性能的提升具有较为显著的效果,由此引出导弹攻击时间控制的导引律问题。
目前,国内外文献对于攻击时间控制导引律的研究,采用不同的理论或技术作为基础,如比例导引法[1-3]、Lyapunov稳定性理论[4-5]、最优控制理论[6]以及成型技术[7-8]等。近年来,现代控制理论特别是滑模控制理论的发展为设计具有终端约束的导引律提供了一种新方法[9-12]。文献[9]通过构造由攻击时间误差和视线角速率组成的滑模面,提出一种滑模攻击时间控制导引律;文献[10]仅将攻击时间误差作为滑模面,推导了一种用于攻击时间控制的非奇异滑模导引律;文献[11]针对多弹协同攻击问题提出了一种滑模导引律;文献[12]基于滑模理论设计了一个考虑视场角约束的二维攻击时间控制导引律。
实际工程应用中,在设计攻击时间控制导引律时必须要考虑导引头的视场角约束[4,12-14]。一般而言,考虑视场角约束的攻击时间控制导引律设计可以分为两类:第一类的设计原则是始终保持导弹前置角减小,从而确保满足视场角约束,文献[4]即属于第一类;文献[12-14]则属于第二类,该类导引律始终保持导弹前置角不超过视场角边界值,相应地,当前置角达到边界值时,前置角速率必须小于零。上述第一类导引律较为简单,易于实现,但会受到初始前置角的影响,当初始前置角为零时不能实现攻击时间控制,并且攻击时间的可控范围也受初始前置角大小的约束。文献[12]通过采用滑模技术,解决了初始前置角为零时不能实现攻击时间控制的奇点问题。
在前面提到的文献中,除文献[5]之外,其他文献都是在二维平面中设计攻击时间控制导引律。对于三维情形,通常将导弹的运动分解为两个正交的二维平面运动,在每个二维平面内单独设计导引律。然而,已有研究表明,直接在三维空间中设计不依赖于解耦的导引律是更为有效的方式。文献[15]首先解决了三维纯比例导引律的设计问题;文献[16]则针对静止和非机动目标,分析了三维纯比例导引法的性能。近年来,越来越多的研究者关注三维空间中攻击角度控制的问题[16-19]。相对而言,只有较少研究[5,20]涉及三维攻击时间控制导引律。文献[5]基于Lyapunov理论设计的三维攻击时间控制导引律,在零初始前置角条件下存在奇点,并且没有考虑导引头视场角约束。文献[20]基于最优控制理论和比例导引法设计的三维攻击时间控制导引律,也未考虑导引头视场角的限制。
综上分析,关于三维攻击时间控制导引律的研究,目前国内外相对较少。考虑到滑模理论自身的优势以及实际工程中三维问题的重要性,有必要对此开展深入研究。本文以导弹非线性模型为基础,采用滑模理论,提出一个考虑视场角约束的无奇点三维攻击时间控制导引律,并对稳定性、收敛性等进行了证明和分析。
1 问题描述
本文考虑导弹在三维空间攻击静止目标的情形,采取与文献[5]类似的假设:①将导弹看作质点;②自动驾驶仪的动态响应比导弹快得多,故自动驾驶仪延迟可以忽略不计;③导弹速度为恒定值;④只考虑垂直于导弹速度矢量的法向加速度。
1.1 坐标系及其相互转换
导弹M和静止目标T的三维几何关系如图1所示。图中,R为弹目距离;VM为导弹速度;aM为导弹法向加速度;φM为前置角,定义为导弹速度矢量与三维空间中导弹视线角矢量之间的夹角。

图1 对于静止目标的三维弹目几何关系Fig.1 Three-dimensional engagement geometry for a stationary target
为描述导弹与静止目标间的三维运动学关系,定义三个坐标系:参考坐标系(表示为Mxyz)、导弹弹体坐标系(表示为MxMyMzM)以及视线坐标系(表示为MxLyLzL)。坐标系之间的转换关系如图2所示。
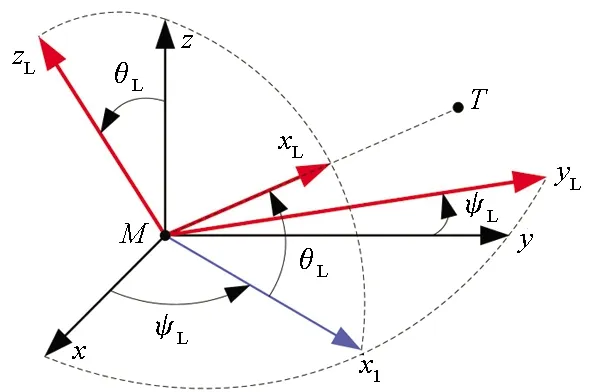
(a) 参考坐标系转换为视线坐标系(a) Transformation between reference coordinate system and line-of-sight coordinate system

(b) 视线坐标系转换为弹体坐标系(b) Transformation between line-of-sight coordinate system and body coordinate system图2 坐标系的转换关系Fig.2 Transformations of coordinate systems
三种坐标系原点均为导弹质心M。弹体坐标系的xM轴指向导弹的速度矢量方向,视线坐标系的xL轴指向目标并与视线角矢量共线。参考坐标系Mxyz与视线坐标系MxLyLzL相差两个角度,即ψL和θL;视线坐标系MxLyLzL与弹体坐标系MxMyMzM也相差两个角度,即ψM和θM。上述坐标系之间对应的转换矩阵分别为
(1)
(2)
其中:
1.2 控制方程组
基于上述假设和坐标系,可建立如下控制方程组:
(3)
(4)
(5)
(6)
(7)
cosφM=cosθMcosψM
(8)
式中:ayM和azM分别表示导弹的偏航加速度和俯仰加速度;变量上的点表示关于时间的一阶导数。
需要指出的是,对于视场角约束下的攻击时间控制问题,所能实现的攻击时间td存在一定的范围,即I={td∈R:tdmin≤td≤tdmax},其中,tdmin和tdmax为正常数,分别表示可实现的最小和最大攻击时间,且tdmin>R0/VM(下标0表示初始值)。为便于研究,在第1节所列4条假设的基础上,补充如下假设:①导弹的初始前置角满足|φM0|<φmax(其中φmax是由导引头视场角边界所确定的常数);②所需攻击时间td选取合适,使得td∈I。
故本文研究问题可描述为:设计一种带有攻击时间和导引头视场角约束的三维导引律,使得导弹在所需攻击时间td时刻击中目标,同时在整个制导过程(即t∈[0,td])中保持|φM(t)|≤φmax。
2 导引律设计
本节首先基于滑模理论推导出考虑视场角约束的三维攻击时间控制导引律;然后对导引律进行修正,消除零初始前置角引起的奇点;最后对稳定性和收敛性进行证明。
2.1 导引律推导
为实现三维空间中的攻击时间控制,以攻击时间误差设计滑模面s,即
s=t+tgo-td
(9)
式中:t表示当前时间,tgo表示剩余飞行时间。
本文采用式(10)估算剩余飞行时间:
(10)
式中:N为导航增益。
需要说明的是,上述剩余飞行时间估算公式是以文献[2]中的二维估算方法为基础,将文献[2]所用二维比例导引律扩展为三维比例导引律,得到了形式上与文献[2]估算公式相同的三维剩余飞行时间估算公式,只是公式中的φM采用本文式(8)计算得到。
对式(9)关于时间t求一阶导数,得
(11)
对式(10)关于时间t求一阶导数并代入式(11),可得
(12)
根据式(8),可推出
(13)
将式(13)及控制方程组(3)~(8)的相关表达式代入式(12),经推导可得

(14)
其中:
(15)
为保证所设计导引律的Lyapunov稳定性,设计如下三维导弹加速度指令aM
(16)
(17)
(18)
(19)
(20)
其中:k1为正常数。
2.2 导引律修正
当导弹初始前置角为零(即φM0=0)时,俯仰和偏航加速度指令将在整个制导过程中始终保持为零(azM=ayM=0),导弹将沿弹目连线飞行,无法实现对攻击时间的有效控制。因此,需对导引律进行修正,以消除该奇点。
(21)
式中:k2为一正常数;sgn(·)为一符号函数,定义为
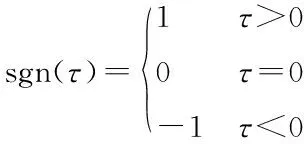
(22)
故导弹加速度指令可表示为
(23)
即
k2[1-sgn(|φM|)]sgn(s)
(24)
k2[1-sgn(|φM|)]sgn(s)
(25)
其中:
值得说明的是,导弹剩余飞行时间与其飞行过程中的距离R和前置角φM有关,而导弹加速度又影响前置角的变化速率。因此,当导弹速度VM及导航增益N确定时,攻击时间存在一定范围,影响该范围的主要因素包括距离R、导引头视场角边界值φmax以及导弹最大过载aMmax。当导引头视场角边界值φmax∈(0,π/2)时,制导过程中弹目距离始终减小,此时所能控制的攻击时间是有界的。攻击时间范围的上、下界可分别利用导弹的最长和最短飞行轨迹除以导弹速度得到。导弹的最长轨迹可分为三段,首先以最大过载飞行,当迅速达到视场角边界值后,保持视场角边界值飞行,最后以最大过载按圆周导引律飞行直至击中目标;而导弹的最短轨迹可分为两段,先是以最小转弯半径飞行,当速度指向目标后,再沿弹目连线飞行。求解两种轨迹的具体方法参见文献[13],这里不再赘述。当φmax∈[π/2,π)时,制导过程中弹目距离有可能是增大的,理论上讲,此时所能控制的攻击时间无上界。
2.3 稳定性证明
为证明所设计加速度指令具有Lyapunov稳定性,构造如下关于s的Lyapunov函数
(26)
对式(26)关于时间求一阶导数,并将式(14)代入,可得

(27)
将式(24)和式(25)代入式(27),经一系列推导,可得
(28)
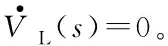
(29)

2.4 收敛性证明
为证明所设计导引律能够满足视场角约束,构造如下关于φM的Lyapunov函数
(30)
对式(30)关于时间求一阶导数,并将式(24)和式(25)代入,可得
(31)
当 |φM|=φmax时, 式(31)为
(32)
定义如下关于变量α的函数
(33)
证明:当α∈(0,π)时,f(α)>0成立。
1)当α∈[π/2,π)时,f(α)>0显然成立;
2)当α∈(0,π/2)时,对式(33)关于α求一阶和二阶导数,有
(34)
(35)
显然,当α∈(0,π/2)时,f″(α)>0成立。当α∈(0,π/2)时,f′(0)=0,f′(α)>0成立。因此,α∈(0,π/2)时,f(α)>0成立。
□
利用上述证明结果,不等式
(36)
恒成立。
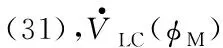
因此,在|φM0|<φmax条件下,式(24)和式(25)可在视场角约束下实现攻击时间控制。
3 关于导引律的相关分析
3.1 参数k1的选取
根据前面的推导,攻击时间误差的变化速率可表达为
(37)


(38)
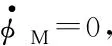
(39)
式中:下标“0”表示初始值。
3.2 与纯比例导引法的关系
根据文献[7-8],如果攻击时间控制导引律中所用剩余飞行时间是基于比例导引法进行估算的,其弹道轨迹终将演变为比例导引法的轨迹。为说明剩余飞行时间估算式(10)应用于本文三维导引律的合理性,有必要检验所提导引律与纯比例导引法之间的关系。

(40)
(41)
显然,当s收敛到零时, 所提导引律与纯比例导引法具有完全相同的形式,由此表明本文所设计导引律的弹道轨迹与具有任意导航增益三维比例导引法的轨迹相同。因此,本文采用剩余飞行时间估算式(10)设计三维攻击时间控制导引律是合理的。
3.3 与解耦三维攻击时间控制导引律的关系
根据前述推导,本文导引律是在三维空间直接设计而无须解耦。若仅考虑俯仰平面内的二维导引问题,偏航平面内的加速度指令变为ayM=0,并且有ψM=0°,φM=θM。将ψM=0°,φM=θM代入导引律 (25),得到俯仰平面内的加速度指令为
(42)
式中:c3=-k2[1-sgn(|θM|)]·sgn(s)。
如果在偏航平面内采用纯比例导引法,即
(43)
则式(42)~(43)构成考虑视场角约束的解耦三维攻击时间控制导引律,即俯仰平面和偏航平面的导引律均独立设计。本文将在仿真部分对比耦合导引律(24)~(25)与解耦导引律(42)~(43)的性能。
4 数值仿真
4.1 性能验证
仿真条件:导弹速度VM=250 m/s,导弹最大加速度为100 m/s2,导弹初始位置(0 m,0 m,0 m),目标位置(6 000 m,6 000 m,0 m),导引头视场角边界值φmax=45°,导航增益N=3,参数k1=3.5,k2=1。三个算例的初始条件和所需攻击时间分别为:①φM0=0°,td=38 s;②φM0=40.1°,td=41 s;③φM0=40.1°,td=35 s。前置角φM0=0°和φM0=40.1°时对应的纯比例导引法攻击时间分别为33.94 s和35.67 s。仿真结果如图3所示。
由仿真结果可知,图3中三种算例的实际攻击时间分别为37.993 9 s、 40.990 6 s、35.009 2 s,与所需攻击时间的误差分别为0.006 1 s、0.009 4 s、0.009 2 s,误差可以忽略,故本文实现了攻击时间控制,且估算的剩余飞行时间满足控制精度要求。由图3(a)~(e)可知,当攻击时间误差大于零时,导引指令通过加快前置角减小的速度来实现攻击时间控制;当攻击时间误差小于零时,导引指令通过在满足视场角约束下增大前置角,从而调节所需攻击时间。在其他相同条件下,所需攻击时间越大,制导过程中前置角在极值附近的时间也越长。另外,在制导过程中,导弹的加速度指令均未达到饱和(限制值取为100 m/s2)。对于初始前置角为零的情形,本文设计的三维导引律也可有效适应。
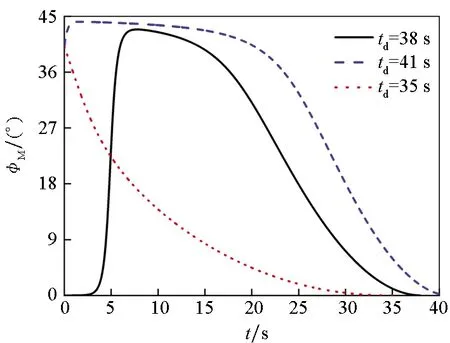
(a) 前置角(a) Heading error

(b) 攻击时间误差(b) Impact time error

(c) 偏航方向加速度指令(c) Acceleration in yaw

(d) 俯仰方向加速度指令(d) Acceleration in pitch

(e) 三维弹道轨迹 (e) Three-dimensional trajectory图3 不同td值对应的三维导引律仿真结果Fig.3 Three-dimensional simulation results with various td
4.2 导航增益对导引律的影响
根据式(10),剩余飞行时间估算公式受导航增益N的影响,故导引律加速度指令的具体值也取决于导航增益值。因此,有必要研究导航增益对所提导引律性能的影响。数值仿真条件如下:初始角度θM0=20°,ψM0=20°,所需攻击时间td=40 s,取参数k1=4,k2=2,其他同第4.1节。相同仿真条件下,N取2,3,4时对应的纯比例导引法攻击时间分别为35.33 s, 34.77 s, 34.53 s。仿真结果如图4所示。
图4结果表明,本文所设计导引律在不同导航增益下均有效,攻击时间误差小于0.01 s。导航增益N=2时,俯仰和偏航方向的加速度指令在弹道终点不能收敛到零值;当导航增益N>2时,两个方向的终端加速度指令值可收敛到零值。这表明,所设计的攻击时间控制导引律在实际应用时,应根据需要选取合适的导航增益值。

(a) 前置角(a) Heading error
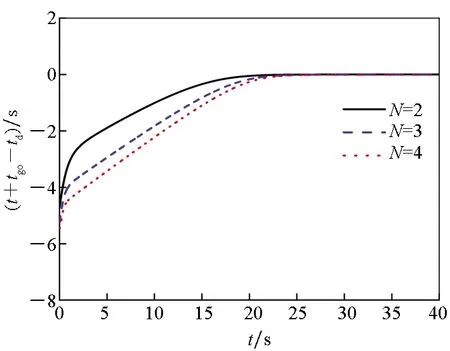
(b) 攻击时间误差(b) Impact time error

(c) 偏航方向加速度指令(c) Acceleration in yaw

(d) 俯仰方向加速度指令(d) Acceleration in pitch图4 不同导航增益下的三维导引律仿真结果Fig.4 Three-dimensional simulation results with various navigation gains
4.3 与解耦导引律的仿真对比
为对比耦合导引律(24)~(25)和解耦导引律(42)~(43),选取三个算例:算例1——θM0=20°,ψM0=0° ;算例2——θM0=20°,ψM0=20°;算例3——θM0=20°,ψM0=40°。算例1是在俯仰平面内;算例2中,俯仰和偏航平面之间具有中等程度的耦合性;算例3中,两个平面之间具有较强的耦合性。取所需攻击时间td=42 s,参数k1=4,k2=1,其余同第4.1节。仿真结果如表1和图5所示。

表1 不同算例对应的控制能量Tab.1 Control energy for various examples 单位:m2/s3

(a) 前置角(a) Heading error
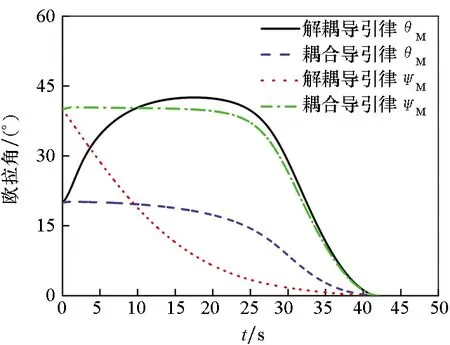
(b) 欧拉角(b) Euler angles
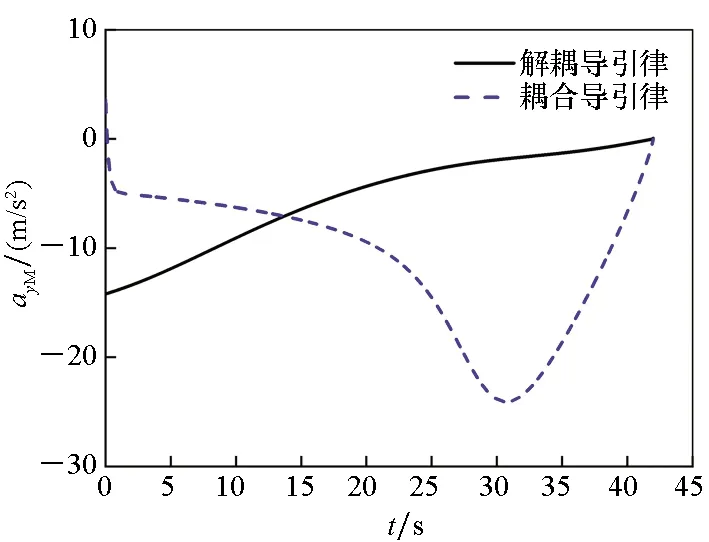
(c) 偏航方向加速度指令(c) Acceleration in yaw
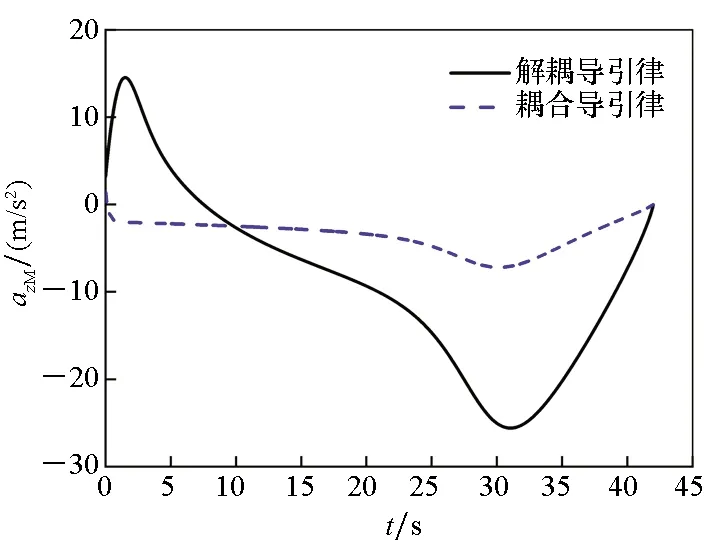
(d) 俯仰方向加速度指令(d) Acceleration in pitch图5 采用不同三维导引律的算例3仿真结果Fig.5 Simulation results of various three-dimensional guidance laws for example 3
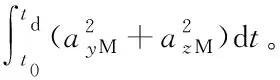
由表1可知,由于能够自动分配加速度指令,耦合三维导引律对应的控制能耗更小,特别是随着俯仰和偏航平面耦合程度的增强,这一优势更为明显。图5给出了算例3的仿真结果。
如图5所示,两种三维导引律都能够在视场角约束下实现攻击时间控制。所设计的耦合三维导引律可自动将加速度命令分配到俯仰和偏航两个通道中。由图5(c)和图5(d)可知,耦合三维导引律主要在偏航平面内进行攻击时间控制,而解耦三维导引律主要在俯仰平面内进行攻击时间控制。
5 结论
针对导弹攻击时间控制的三维导引律设计开展了研究。在导弹非线性数学模型的基础上,直接在三维空间设计出一个耦合的攻击时间控制滑模导引律,并通过对所设计制导律进行简单修正,解决了零初始前置角引起的奇点问题。理论分析及数值仿真结果表明:①所设计的滑模导引律能够在三维条件下有效实现攻击时间增大或减小的控制,并可适应不同的导航增益值;②所设计的滑模导引律能够同时满足视场角约束和攻击时间控制的Lyapunov稳定性条件;③与解耦三维导引律相比,所设计的耦合三维导引律控制能耗更小。
本文的研究为视场角约束条件下的三维攻击时间控制导引律设计提供了一个思路,可作为对当前相关研究的一点补充。

