面向复杂几何模型的多级并行四面体网格生成算法*

徐 权，刘田田，冷珏琳，杨 洋，郑 澎

(1. 中物院高性能数值模拟软件中心， 北京 100088； 2. 北京应用物理与计算数学研究所， 北京 100094；3. 中国工程物理研究院计算机应用研究所， 四川 绵阳 621900)

近年来，高性能计算机发展得非常快，预计国内外将会有多台E级超级计算机研制成功，这些超级计算机的研制为高性能数值模拟的发展提供了必需的硬件环境。随着高性能计算机的发展，国内外的研究人员已开发出诸多适应于高性能计算机的并行数值模拟软件，同时也研制出了数值模拟领域的并行编程框架，如JASMIN[1]、JAUMIN[2]、PHG[3]等，这些编程框架均可以支持并行数值模拟程序的快速开发，使得应用程序快速扩展至数万到数十万处理器核。目前，在计算流体力学、复杂电磁环境、反应堆、大型工程力学分析等领域进行高精度的数值模拟所需的网格规模已高达数十亿量级，而网格生成作为数值模拟中的重要一环，其发展则相对滞后于高性能计算机和数值模拟解法器的发展，针对并行网格生成算法的研究相对较少，国内外尚没有比较成熟的适用于高性能计算机体系结构的并行网格生成软件，而传统的网格生成方法或软件已经不能满足高性能数值模拟的需求，因此需要面向高性能数值模拟研究复杂几何模型的超大规模非结构网格并行生成方法，并与领域编程框架和并行数值模拟求解器实现无缝对接。

前沿推进方法(Advancing Front Technique, AFT)和Delaunay三角化方法是目前非结构四面体网格生成最常用的两种方法，国内外研究人员基于这两种方法已经开发出一批比较成熟的串行四面体网格生成软件，如TetGen[4]、Gmsh[5]、Netgen[6]等，并得到了广泛应用。当前并行四面体网格生成算法的研究主要基于AFT和Delaunay三角化开展，如：Löhner等[7-8]发展了并行前沿推进方法，提出了一种新的可扩展的并行前沿推进方法，并对当前AFT方法的发展趋势进行了展望；Chrisochoides等[9]则基于其团队多年的研究，提出了多级并行的Delaunay三角化方法，该方法可以适应于当前的高性能计算机体系结构，可扩展性较好，但需要复杂的通信和调度机制，编程难度较大；Ivanov、Chen等[10-11]分别提出了基于区域分解的并行网格生成方法，该方法一般需要对面网格进行区域分解，但会引入人工界面，算法的可扩展性较低；Pebay、Wang等[12-13]提出了基于初始网格的并行网格加密方法，该方法在进程间无须进行通信，具有良好的可扩展性，但网格质量相对较差；文献[14-16]则分别提出了基于共享内存的多线程并行四面体网格生成方法。

目前的超级计算机普遍采用分布式-共享内存结构，计算节点之间是分布式内存，计算节点内部是共享式内存，每个计算节点上分布多个中央处理器(Central Processing Unit, CPU)，每个CPU内分布多个核，如图1所示。采用分布式算法和共享内存算法耦合的并行网格生成可以更好地适应当前的高性能计算机体系结构，同时可以有效提高网格生成算法的可扩展性。

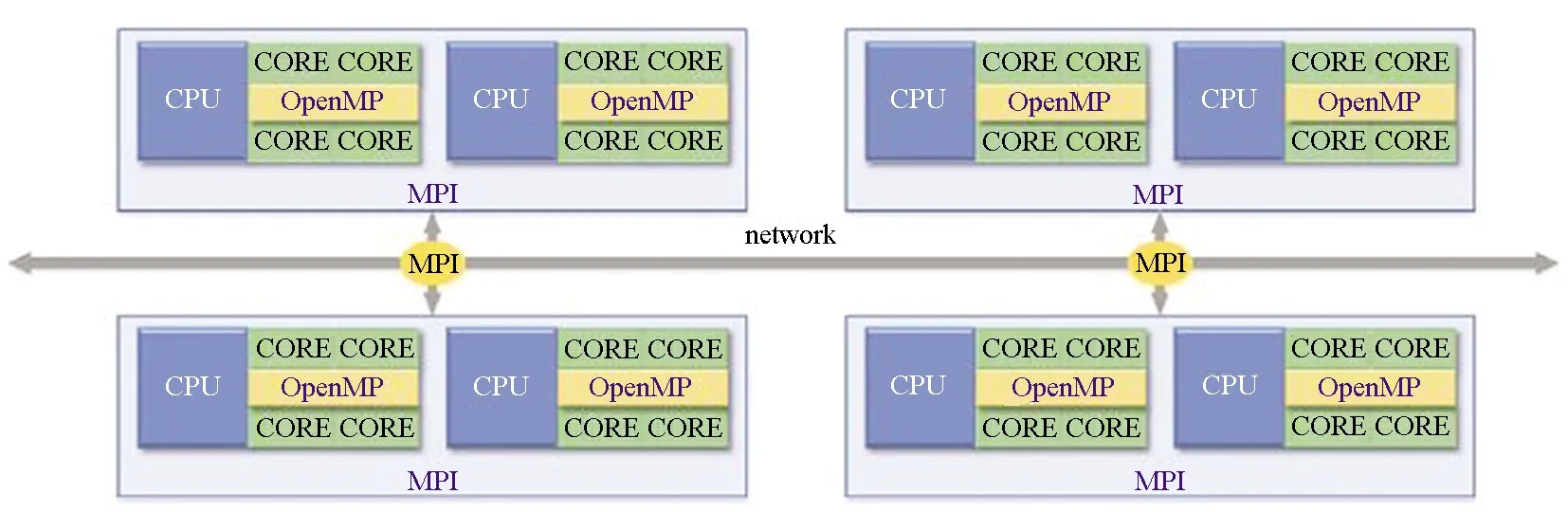
图1 主流超级计算机的体系结构Fig.1 Architecture of current major supercomputers

本文针对高性能数值模拟领域对数十亿乃至上百亿四面体网格生成的需求，提出了一种适用于复杂几何模型的多级并行四面体网格生成框架，同时提出了面向几何实体的区域分解方法和多实体间的并行面网格生成方法，在生成四面体网格时复用了基于三角形网格的区域分解和多线程四面体网格生成方法。该算法可以适应现有的高性能计算机体系结构，实现多实体复杂几何模型的大规模四面体网格的并行生成。

1 多级并行四面体网格生成

1.1 并行网格生成框架

本文的多级并行四面体网格生成算法是基于中物院高性能数值模拟软件中心研制的并行数值模拟前处理软件SuperMesh[17]研发的。SuperMesh是一款面向大规模复杂数值模拟的并行前处理引擎，它以“可计算几何模型”为核心，建立了模型的统一表达方式，屏蔽了底层各种几何核心，发展了模型处理和网格生成两大子系统，具备面向复杂几何模型的结构网格、非结构网格、组合几何的并行生成能力，支持应用软件前处理界面的快速定制，支持与并行领域编程框架JASMIN、JAUMIN和数值模拟应用程序的无缝对接，从而支持大规模的数值模拟。

基于并行前处理引擎SuperMesh，提出了面向复杂几何模型的适应高性能计算机体系结构的多级并行四面体网格生成框架，该框架的整体流程如图2所示。首先是对计算机辅助设计(Computer Aided Design, CAD)模型进行模型处理，使模型转换为可计算几何模型，然后自动识别模型的几何特征，建立网格的尺寸场，基于尺寸场和几何实体间的邻接关系对CAD模型的几何实体进行分组，并将分组后的几何实体分配到不同的计算节点中，各节点之间并行生成三角形面网格，接着在每个计算节点内对三角形面网格进行二次区域分解，分解为多个子面网格，并将分解后的子面网格分配到各进程中，最后每个进程内采用多线程并行四面体网格生成方法实现大规模非结构四面体网格的生成。下面将对算法流程中的关键算法进行介绍。

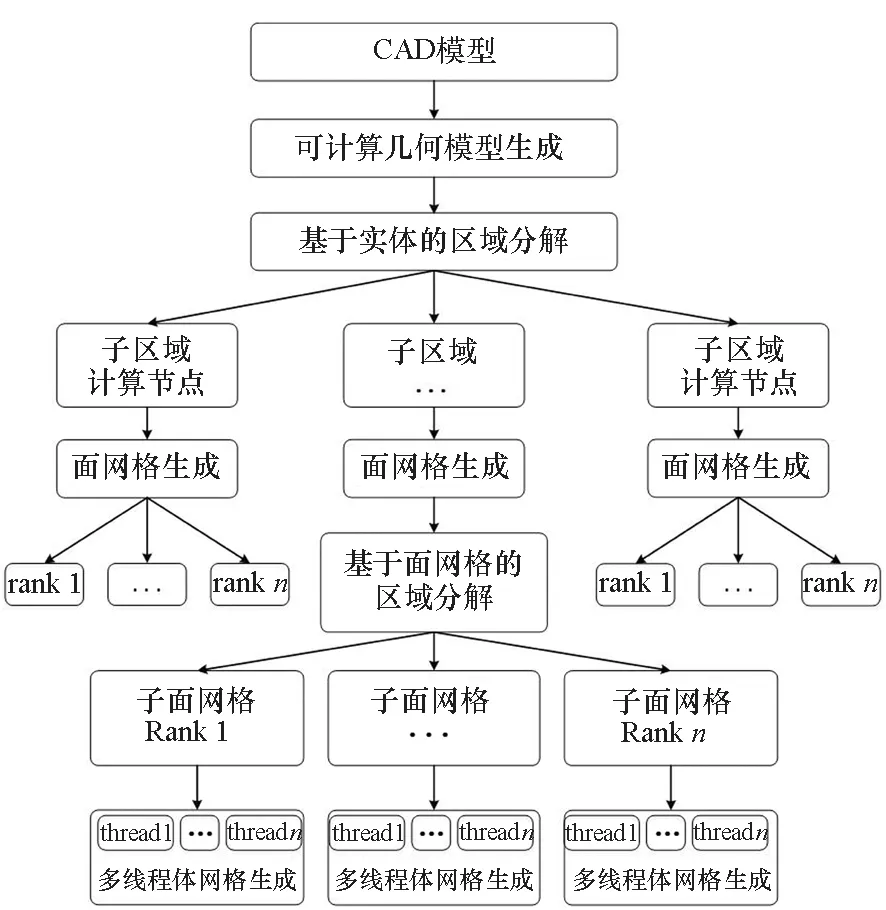
图2 多级并行四面体网格生成流程Fig.2 Flow chart of multilevel parallel tetrahedral mesh generation

1.2 基于几何实体的区域分解

在实际工程应用中，CAD模型一般均是装配体，装配体包含了CAD模型的建模过程信息，并由多个几何实体组成。为了提高并行网格生成方法的可扩展性，本文针对含多个几何实体的CAD模型提出了基于几何实体的区域分解方法，该方法可以保证网格生成中几何实体的完整性和四面体网格的质量。在对CAD模型进行分组时，需要考虑两方面因素：①减少计算节点间的通信；②保证计算节点间的负载平衡。为了减少通信，需要减少不同区域间的交界面的个数，即将相邻的几何实体分配到同一个计算节点，为此在分组时考虑了几何实体间的邻接关系。为了保证网格生成的负载平衡，本方法首先建立了网格的尺寸场，然后基于尺寸场对每个几何实体的网格规模进行了预估，并在构建无向图时作为图中节点的权重，从而达到良好的负载平衡。基于几何实体的区域分解算法步骤如算法1所示，流程如图3所示。

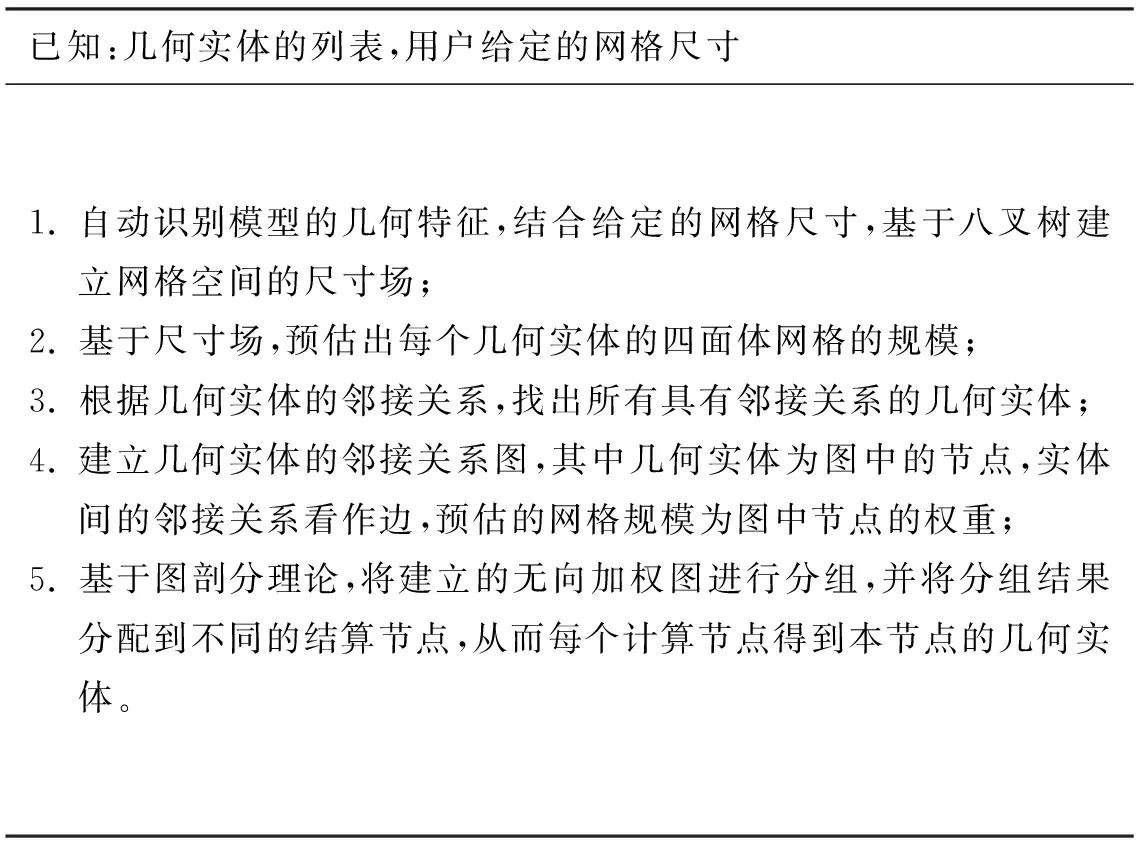
算法1 基于几何实体的区域分解算法Alg.1 Algorithm of domain decomposition based on geometric entities

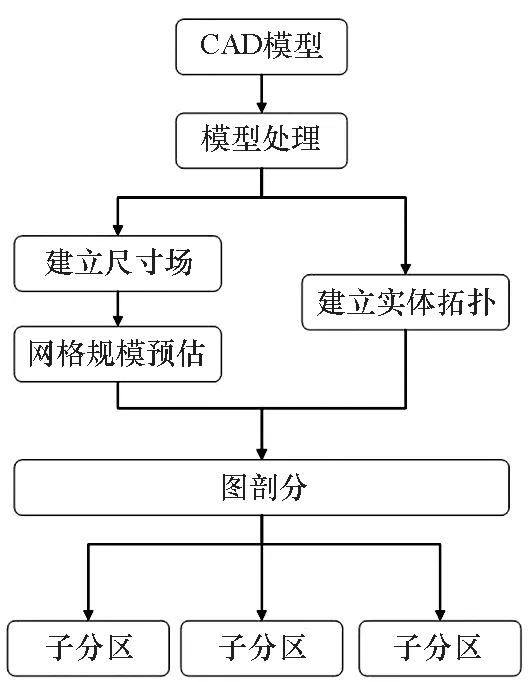
图3 基于几何实体的区域分解流程Fig.3 Flow chart of domain decomposition based on geometric entities

针对包含1 876个几何实体的三峡大坝模型进行了测试，测试使用24个处理器核，分别对无网格规模预估和加入网格规模预估进行了测试，两次测试生成的四面体网格数分别为3 374万和3 348万。图4给出了加入网格规模预估前后的每个处理器核内的网格数，可以看出加入网格规模预估后，不同处理器核上网格分布更加均匀，相比未进行网格规模预估的情况，整体上网格的负载平衡得到大大改善。

图4 加入网格规模预估前后网格数对比Fig.4 Comparison of number of cells before and after mesh size prediction

1.3 并行三角形面网格生成

目前的数值模拟求解方法大都需要协调地计算网格，为了保证协调四面体网格的生成，需要保证子区域交界面上网格的一致，为此在并行三角形网格生成过程中，需要对每个节点上的边界进行处理，从而保证节点间网格的协调一致。在并行前处理引擎SuperMesh中，已经研制了面向复杂几何模型的“线—面—体”的三步分离式串行四面体网格生成算法，本文对该算法进行了扩展，实现了节点间“点—线—面”三角形网格的并行生成，该算法的步骤如算法2所示，流程如图5所示。在计算节点内实现“点—线—面”网格后，对于不同的子区域间共享的节点、线和面，通过并行通信模块使得节点间交界面上网格一致，从而保证协调的三角形网格生成。

算法2 并行三角形网格生成算法Alg.2 Algorithm of parallel triangular mesh generation

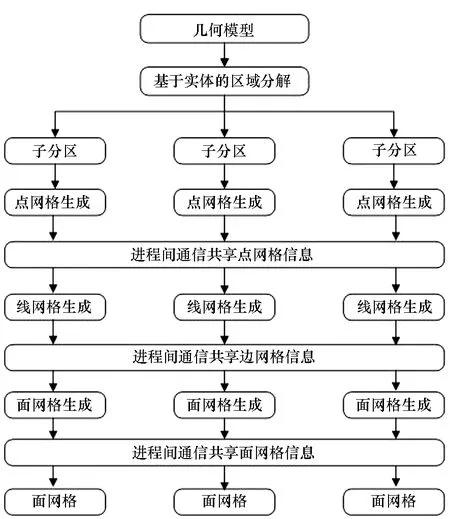
图5 并行三角形网格生成流程Fig.5 Flow chart of parallel triangular mesh generation

1.4 基于三角形网格的区域分解方法

单个几何实体比较复杂时，其需要生成的网格规模会非常大，生成四面体网格时间比较长，此时需要对单个几何实体的三角形面网格做进一步分解，分解为多个较小的子面网格，然后再并行生成四面体网格。本文采用文献[11]提出的基于三角形面网格的区域分解算法，该算法对三角形面网格采用递归的方式依次分解为子区域，每次分解时会在待分解区域内插入一个交界面网格，将区域一分为二，当所有子区域的网格规模都小于给定的阈值时，递归分解过程结束，最终实现面网格的区域分解，并将每个子面网格分发到不同的处理器中。

1.5 多线程四面体网格生成

Delaunay三角化方法由于具备数学基础好、网格生成时间快、网格质量好等优势，得到了广泛的应用。多线程并行Delaunay算法关键是减少网格生成过程中多个点同时插入引起的空腔干涉现象，目前处理的思路基本是先将点集进行分组，然后各线程再并行插点，当两个点同时插入引起空腔干涉时，放弃其中一个线程的操作，直到网格生成结束。但上述方法无法保证负载平衡，且同步等待的时间较长，因此本文采用了文献[16]提出的改进的基于无锁原子操作的并行Delaunay算法，该算法中令每一个四面体单元都附一个原子变量及一个占位标志。在计算Delaunay空腔的过程中，线程将其空腔中所有单元及边界外一层单元的原子变量置为1。若有多个线程同时试图将某个变量置位，则使用无锁原子操作的机制保证有且仅有一个线程成功置位占位变量，在更新四面体单元的相邻关系过程中，此操作仅仅涉及修改局部区域的单元，可以有效减少由于负载不平衡引起的同步等待时间，算法的并行效率较高。

2 数值实验与结果分析

2.1 并行性能与分析

在并行算法性能测试中，并行加速比是较为常用的并行性能测试指标。一般地，并行加速比的定义为

S=T1/TP

其中，T1为单进程网格生成时间，TP为P个进程的并行网格生成时间。

由于测试模型网格生成规模较大，无法在单进程下运行，因此对并行加速比的计算公式进行修正，修正后的并行加速比为

S=(TN/TP)×N

其中，TN为N个进程时网格生成时间。

测试环境为曙光集群系统，该系统共有424个计算节点，系统采用Intel Omni-path高速互联网格、曙光Parastor300全局并行存储系统，每个计算节点均配置2颗Intel Xeon Gold 6132处理器，每个处理器14核，96 GB DDR4 ECC 2400 MHz内存。

测试模型选取了具有代表性的三峡大坝模型对算法进行了数值验证(如图6所示)。三峡大坝模型包含左厂房坝段、泄洪坝段、右厂房坝段、非溢流坝段、升船机、船闸、连接坝段，共计1 876个几何实体。坝顶长度2 309 m，最大坝高181 m，整个模型包含了丰富的几何细节，几何尺寸跨度大，模型比较复杂。

图6 三峡大坝CAD模型图Fig.6 CAD model of Three Gorges Dam

在进行并行测试时，由于集群使用限制，本算法测试主要测试了千核下的并行加速比。测试时每个节点使用28个处理器核，从228个处理器核开始进行测试，测试网格尺寸为0.5 m，生成9.36亿四面体网格单元，并行网格生成时间和加速比分别如表1和图7所示。

表1 三峡大坝模型并行四面体网格生成加速比Tab.1 Speed-up ratio of parallel tetrahedral mesh generation for Three Gorges Dam model

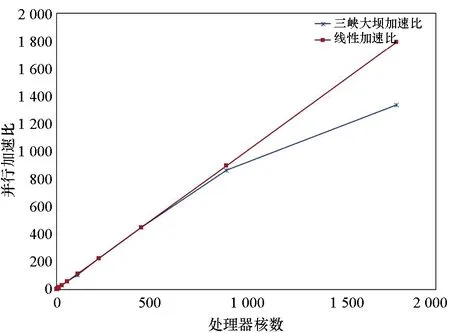
图7 三峡大坝模型四面体网格并行生成加速比Fig.7 Speed-up ratio of parallel tetrahedral mesh generation for Three Gorges Dam model

从表1和图7可以看出，本算法针对三峡大坝模型，可以获得良好的加速比，具备在数千处理器核上并行生成数十亿规模四面体网格单元的能力。

与文献[10-11]等提出的并行四面体网格生成算法相比，本文的算法在448处理器核下，9.36亿四面体网格单元生成时间在5 min以内，整体上网格生成时间相对较少，同时本文的算法可扩展到千核以上，相对文献[10-11]提出的算法具有更好的并行可扩展性。

2.2 四面体网格质量分析

图8 三峡大坝模型四面体网格质量统计结果Fig.8 Statistical results of tetrahedral mesh quality of Three Gorges Dam model

从统计结果中可以看出，并行生成的四面体单元的体积边长比均集中在0.5～0.9的范围，基本不存在扁平的单元(<0.2)，生成的网格质量较高。

2.3 实际应用测试

三峡工程计算规模庞大，千万级单元的模拟只能达到米级，考虑基础、细节构造的高分辨率模拟，需要数十亿自由度级的计算能力，而现有的自主行业软件和商业软件难以满足计算需求。通过本文提出的并行网格生成算法，结合文献[18]提出的并行加密算法，在“天河二号”上，采用49 152处理器核，并行生成101.1亿四面体网格单元，并采用结构静力与振动大规模并行分析软件PANDA-StaVib首次实现了三峡大坝精细模型的静力计算，为三峡大坝工作性态评估提供了能力支撑。图9给出了三峡大坝的网格结果。

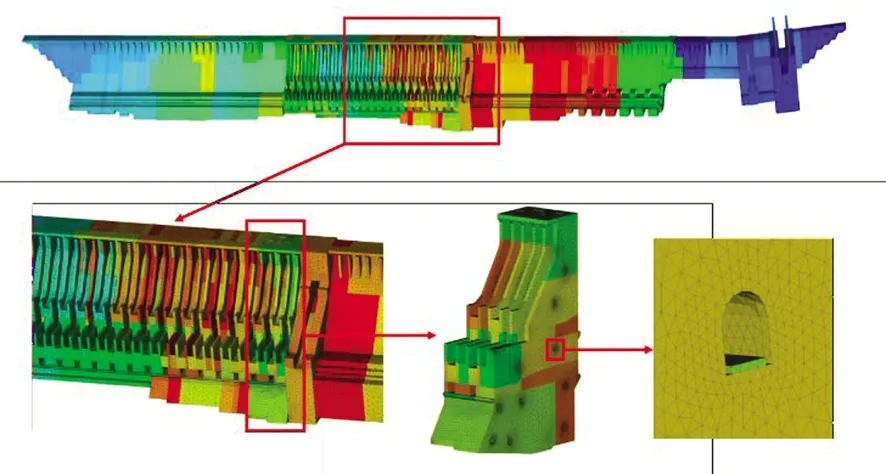
图9 三峡大坝模型四面体网格生成结果Fig.9 Tetrahedral mesh of Three Gorges Dam model

3 结论

面向高性能数值模拟对大规模非结构网格生成的需求，提出了一种适应复杂几何模型的多级并行四面体网格生成框架，并针对装配体模型提出了基于几何实体的区域分解算法和并行面网格生成算法，能适用具有数千上万几何实体的复杂几何模型。在四面体网格并行生成时，该框架可以复用面网格区域分解和多线程四面体网格生成算法，相比单纯的分布式并行算法或共享内存式并行算法，具备良好的并行效率和可扩展性，更好地适应了当前的高性能计算机体系结构，可以在数千处理器核上并行生成数十亿规模四面体网格单元。

本文提出的并行非结构网格生成框架，可以推广到含有多个几何实体的模型的其他类型网格生成算法，如六面体网格、混合网格等，仅需将框架中的三角形网格生成和四面体网格生成的单元算法替换为相应的网格生成算法，具有较好的推广应用价值。