论思维可视化在教学中的实践
王火炬


培养和发展学生的思维能力有许多途径和方法。在具体教学中,可以借助思维可视化的理论,采取相应的策略,助力学生思维能力的培养与训练。让思维可视化,展现“看得见”的思维过程,有利于学生对知识进行理解和记忆,可以有效提高信息加工及信息傳递的效能;对于教师,可以更好地把握学生对知识的理解和掌握程度,可以更加清楚地了解学生获得知识的思路,有利于教师及时发现教学中存在的问题并加以调整,从而促进教学实效。在“数的认识”领域,如何借力思维可视化促进新知识的教与学呢?现以人教版四下“小数的认识”(以下称本课)为例,结合具体的实践,作粗浅的探索。
一、在了解知识的产生由来中实践思维可视化
任何知识的产生都有由来,都有其源起,一般是在一种旧知识无法解决新问题的基础上产生的。要让学生较好地了解和认识这一过程,可以运用思维可视化。
在本课的教学中,教师可引导学生通过动手操作,展现思维的过程,体会小数的产生。可以先让学生拿出米尺,比划出1米的长度。接着提问:如果要量超过一米的东西,你准备怎样量?量出来,你准备怎样表示量出的结果?还能用一个整数直接表示出来吗?生活中,还有类似的例子吗?还可以引导学生称物体的重量,先称整数重量的物体,再称不是整数重量的物体,可以问学生:这时要表示出重量,怎么办?然后让学生在动手操作中,展现出思考和解决问题的过程,抽象出生活中如果无法用整数表示一个数量时,可以用小数来表示。通过巧妙的设问,让学生借助动手操作来思考和探讨问题,教师可以清楚地知道学生的思维过程,并及时有效地予以指导。
二、在体验知识的形成过程中实践思维可视化
数学知识的形成不是天生的,都有一定的探索历程。教学时,一定要注重引导学生体验知识的形成过程,即要引导学生深刻领会和感受新知识是怎么来的,并以此培养学生的探索、创新能力,以及发展学生的归纳、演绎等思维能力。探索知识的形成过程,可以充分利用数形结合、绘制图表等方式实践思维可视化,让学生更好地理解和掌握新知识,让教师更好地把握和调控学生的思维过程。
如本课的教学,笔者先出示一把米尺,引导学生观察一米被平均分成了几份,每一份是多少,用分数怎样表示,然后告诉学生分数十分之一可以写作小数0.1。紧接着问学生:“三分米、七分米用分数、小数可以各怎样表示,各有几个0.1?”让学生在互动中完成教材第32页例1中的几个括号内容的填写(把1 m平均分成10份),最后引导学生小结:十分之几的数都可以写成一位小数,计数单位都是0.1或十分之一。接着,让学生学着刚刚的方法,互相讨论,试着把教材第32页例题括号中的内容填完整(把1 m平均分成100份)。再接着,让学生看教材第33页例题(把1 m平均分成1000份)的尺子与空格,直接口答,并说说有什么发现。最后,让学生将例题中的答案与图像结合到一起,尝试归纳并回答什么样的数可以用小数来表示,分别可以表示几位小数,计数单位分别是多少,如果是万分之几呢。在引导学生探索和体验小数的意义的形成过程中,利用数形结合,学生的思维过程充分暴露和显现,教师及时进行指导和点拨,并引导学生自己讨论、归纳得到结论,更好地培养和发展了学生思维能力。
三、在探索知识的本质特征中实践思维可视化
任何数学知识都有其本质特征,对本质特征有更清楚的把握,就能更好地掌握其内容。教学数学时,要注意引导学生去探讨和感悟新知识的本质特征,加深对新知识的理解。在研究本质特征时,可以借助绘制和完善图表等方式让思维看得见,使实践思维可视化。
如本课,数的意义的本质是计量,即按一定的标准计数,整数是从个、十、百……往一个方向延伸,而小数则从十分之一、百分之一……往另一个方向延伸。小数意义的本质是按0.1、0.01……来计数或数数,这就清晰地区分了它与整数的不同。所以要让学生加深理解,可以让学生尝试着完善下面的图表(表1),并让他们说说整数与小数有什么不同,从表中可看出什么,能否举出一个例子来说明。也可以指导学生完成相应的概念图(图1),带领学生进一步理解小数的本质特征,并使得学生的思维过程充分地展现,从而更好地分析问题和解决问题。
四、在打通知识的前后联系中实践思维可视化
任何知识都不是孤立存在的,都是相互联系的。数学教学中,要充分依托旧知识,借助学生已有的学习经验,做好铺垫,以旧引新,以更有效地完成新知识的学习。在学完新知识之后,可以引导学生通过动手画或者完善知识结构图、系统图的方式实践思维可视化,让学生在打通知识联系、构建知识体系的过程中,充分展现思维过程,培养和发展思维能力。
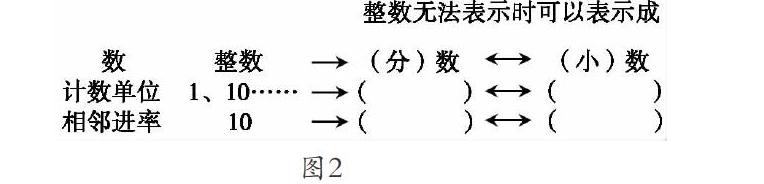
如本课,可以引导学生完成如下结构图(图2),并归纳说出自己的思考和发现。引导学生从计数单位的角度打通和建构整数、分数与小数之间的知识联系,发展学生的思维。
五、在尝试知识的实际运用中实践思维可视化
学习知识,自然是为了运用。如何运用,运用的情况如何,可以依托思维可视化来考查学生学到新知识的情况,也考查学生运用新知识解决实际问题的能力。这就要求我们在引导学生进行知识运用时,不能简单地关注问题解决的结果,更要关注问题解决的过程。问题的设置导向,要让学生不单单解决问题,还可以通过完成相应的图表展现解题思路,如让学生结合绘制几何图、流程图、线段图、模型图来解题,由此展现其思维过程。
如本课,可以设计这样的练习:给你一把米尺,要求你表示出0.5;你会有哪些表示方法,请指出来。有的同学指出5分米是0.5米,有的同学指出50厘米是0.5米,还有的同学在1分米中找出5厘米是0.5分米。这一动手操作是学生运用知识的过程,也在教师考查学生思维的过程。
总之,在数的认识领域,思维可视化还可以有很多的探索和实践,教学中应充分展现、暴露学生的思维过程,以更好地让学生获得新知识,同时培养和发展学生的思维能力,培养和提升学生的核心素养。

