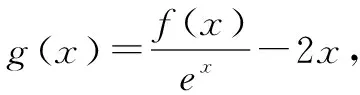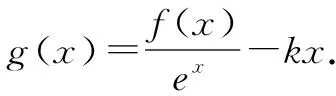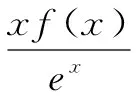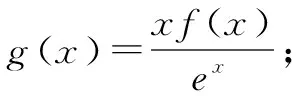构造相关函数 破解一类抽象函数不等式问题
肖志军
(北京工业大学附属中学 100022)
在近几年高考和模拟考试中,常有一类抽象可导函数成为考试的热点,此类试题难度较大,学生往往感到无从下手.若能根据题目条件构造恰当的相关函数,根据条件得出所构造函数的性质,如奇偶性、增减性、周期性等基本性质,即可巧妙地破解此类抽象函数不等式问题,本文结合实例,谈谈构造哪些相关函数,如何构造相关函数.
一、构造和差函数
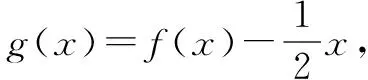
例2 设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(-x)+f(x)=x2,且x∈(0,+∞)时,f′(x)>x.若f(2-a)-f(a)≥2-2a,则实数a的取值范围为( ).
A.[1,+∞) B.(-∞,1]
C.(-∞,2] D.[2,+∞)
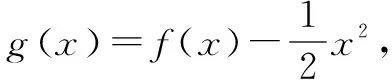
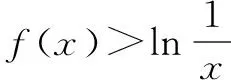
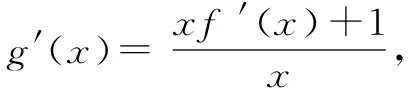
因为f(e)=-1,所以g(e)=f(e)+lne=0;所以当x∈(0,e),g(x)<0,当x∈(e,+∞),g(x)>0.
所以当x∈(e,+∞),则不等式f(x)+lnx>0成立.
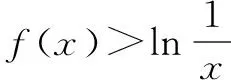
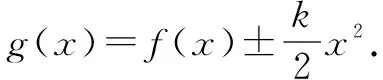
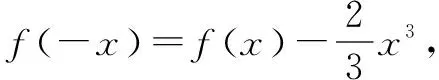
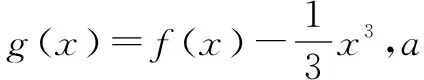
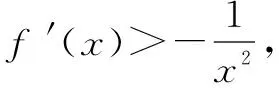
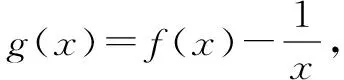
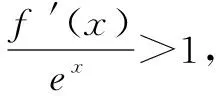
思路点拨构造函数g(x)=f(x)-ex,f(2)-f(1)>e2-e.
二、构造积函数
例7 已知函数f(x)的定义域为(0,+∞),且满足f(x)+xf′(x)>0(f′(x)是f(x)的导函数),则不等式(x-1)f(x2-1) 解析构造函数g(x)=xf(x),其中x>0,则g′(x)=f(x)+xf′(x)>0,所以函数y=g(x)在定义域(0,+∞)上为增函数.在不等式(x-1)f(x2-1) 故不等式(x-1)f(x2-1) 例8 设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)>x2,则不等式(x+2020)2f(x+2020)-9f(-3)>0的解集是____. 解析将不等式(x+2020)2f(x+2020)-9f(-3)>0化为(x+2020)2f(x+2020)>(-3)2f(-3),构造函数g(x)=x2f(x),则上式化为g(x+2020)>g(-3).因为g′(x)=2xf(x)+x2f′(x),由已知2f(x)+xf′(x)>x2,又x∈(-∞,0),所以g′(x)<0,g(x)在(-∞,0)上是减函数,故x+2020<-3,x<-2023. 所以不等式的解集是(-∞,-2023). 具有特征xf′(x)+f(x)时,可构造g(x)=xf(x);具有特征xf′(x)+2f(x)时,可构造g(x)=x2f(x);一般情况,具有特征xf′(x)+kf(x)时,可构造g(x)=xkf(x). 例9 已知奇函数f(x)和其导函数f′(x)的定义域均为R,当x∈(0,+∞)时,3f(x)+xf′(x)<0,则不等式(x-1)3f(x-1)-8x3f(2x)<0的解集为( ). 例10 已知函数f(x)的定义域为R,其图象关于点(-1,0)中心对称,其导函数为f′(x),当x<-1时,(x+1)[f(x)+(x+1)f′(x)]<0,则不等式xf(x-1)>f(0)的解集为( ). A.(1,+∞) B.(-∞,-1) C.(-1,1) D.(-∞,-1)∪(1,+∞) 解析构造函数g(x)=(x+1)f(x),则g′(x)=f(x)+(x+1)f′(x). 因为当x<-1时,(x+1)[f(x)+(x+1)f′(x)]<0,所以当x<-1时,f(x)+(x+1)f′(x)>0,则g(x)在(-∞,-1)上递增.因为函数f(x) 的定义域为R,其图象关于点(-1,0)中心对称,所以函数f(x-1)的图象关于点(0,0)中心对称,则函数f(x-1)是奇函数,令h(x)=g(x-1)=xf(x-1),所以h(x)是R上的偶函数,且在(-∞,0)递增,由偶函数的性质得:函数h(x)在(0,+∞)上递减.因为h(1)=f(0),所以不等式xf(x-1)>f(0)化为h(x)>h(1),即|x|<1,解得-1 具有特征(x+1)f′(x)+f(x)时,可构造g(x)=(x+1)f(x).一般情况,具有特征(x+k)f′(x)+f(x)时,可构造g(x)=(x+k)f(x). A.(-1,0)∪(1,2019) B.(-2019,-1)∪(1,2019) C.(0,2019) D.(-1,1) 可知不等式的解集为(0,2019),故选C. 例12已知定义在R上的连续函数f(x)满足f(x)=f(4-x),且f(-2)=0,f′(x)为函数f(x)的导函数,当x<2时,有f(x)+f′(x)>0,则不等式x·f(x)>0的解集为( ). A.(0,6) B.(-2,0) C.(-∞,-2) D.(-∞,-2)∪(0,6) 解析构造函数g(x)=exf(x)(x<2),则g′(x)=exf(x)+exf′(x)=ex[f(x)+f′(x)]>0,g(x)在(-∞,2)单调递增,且g(-2)=e-2f(-2)=0,当x∈(-∞,-2)时,g(x)<0;当x∈(-2,2)时,g(x)>0.又ex>0,当x∈(-∞,-2)时,f(x)<0;当x∈(-2,2)时,f(x)>0,又f(x)满足f(x)=f(4-x),所以f(x)图象关于直线x=2对称,所以当x∈(-2,6)时,f(x)>0;当x∈(-∞,-2)∪(6,+∞)时,f(x)<0. 解得x∈(-∞,-2)∪(0,6),故选D. 具有特征f′(x)+f(x)时,可构造g(x)=exf(x);具有特征f′(x)+2f(x)时,可构造g(x)=e2xf(x).一般情况,具有特征f′(x)+kf(x)时,可构造g(x)=ekxf(x). 例13 定义在R上的函数f(x)满足e4(x+1)f(x+2)=f(-x),且对任意的x≥1都有f′(x)+2f(x)>0(其中f′(x)为f(x)的导数),则下列一定判断正确的是( ). A.e2f(2) C.e4f(4) 思路点拨构造函数g(x)=e2xf(x),选B. 所求不等式的解集为(1,+∞). 例15设f′(x)是偶函数f(x)(x≠0)的导函数,当x∈(0,+∞)时,xf′(x)-2f(x)>0,则不等式4f(x+2019)-(x+2019)2f(-2)<0的解集为( ). A.(-∞,-2021) B.(-2021,-2019)∪(-2019,-2017) C.(-2021,-2017) D.(-∞,-2019)∪(-2019,-2017) 例16 设f′(x)是奇函数f(x)(x≠0)的导函数,f(-1)=0,当x<0时,xf′(x)-3f(x)>0,则使得f(x)<0成立的x的取值范围是( ). A.(-1,0)∪(0,1) B.(-∞,-1)∪(1,+∞) C.(-1,0)∪(1,+∞) D.(-∞,-1)∪(0,1) 例17已知f(x)为R上的可导函数,且对任意的x∈R,均有f(x)>f′(x),则有( ). A.e2020f(-2020) B.e2020f(-2020) C.e2020f(-2020)>f(0),f(2020)>e2020f(0) D.e2020f(-2020)>f(0),f(2020) A.(-∞,1) B.(-∞,e) C.(1,+∞) D.(e,+∞) 例19 设f(x)是定义在R上的函数,其导函数为f′(x),若f(x)+f′(x)>1,f(0)=2018,则不等式exf(x)>ex+2017(其中e为自然对数的底数)的解集为____. 解析构造函数g(x)=ex[f(x)-1],则g′(x)=exf(x)+exf′(x)-ex=ex[f(x)+f′(x)-1]. 因为f(x)+f′(x)>1,所以f(x)+f′(x)-1>0,即g′(x)>0,g(x)在R上单调递增.因为g(0)=f(0)-1=2018-1=2017,所以原不等式可化为g(x)>g(0). 由g(x)的单调性得x>0,所求解集为(0,+∞). 具有特征f(x)-1+f′(x)时,可构造g(x)=ex[f(x)-1];具有特征2[f(x)-1]+f′(x)时,可构造g(x)=e2x[f(x)-1].一般情况,具有特征k[f(x)-1]+f′(x)时,可构造g(x)=ekx[f(x)-1];具有特征k[f(x)-m]+f′(x)时,可构造g(x)=ekx[f(x)-m]. 例20 已知函数f(x)(x∈R)的导函数为f′(x),若2f(x)+f′(x)≥2,且f(0)=8,则不等式f(x)-7e-2x>1的解集为( ). A.(-∞,0) B.(0,+∞) C.(-∞,-1)∪(0,+∞) D.(1,+∞) 解析构造函数g(x)=e2x[f(x)-1],选B. 例21已知e为自然对数的底数,定义在R上的函数f(x)满足f′(x)-f(x)<2ex,其中f′(x)为f(x)的导函数,若f(2)=4e2,则f(x)>2xex的解集为( ). A.(-∞,1) B.(-∞,2) C.(1,+∞) D.(2,+∞) 所以f(x)>2xex的解集为(-∞,2).故选B. 例22已知定义在R上的可导函数f(x)的导函数为f′(x),对任意实数x均有(1-x)f(x)+xf′(x)>0成立,且y=f(x+1)-e是奇函数,不等式xf(x)-ex>0的解集是____. 例23 设f(x)是定义在R上的函数,其导函数为f′(x),若f(x)-f′(x)<1,f(0)=2016,则不等式f(x)>2015·ex+1(其中e为自然对数的底数)的解集为( ). A.(-∞,0)∪(0,+∞) B.(0,+∞) C.(2015,+∞) D.(-∞,0)∪(2015,+∞) 构造函数是一种创造性的方法,它较好地体现了数学中函数与方程思想、转化与化归思想,渗透着猜想、实验、特殊化、探索等数学研究手段.同时,构造函数又是一种行之有效的方法,具有较大的灵活性和技巧性,根据要解决的问题,充分利用已知条件,灵活转化、恰当构造,有的放矢,从而使问题得以突破.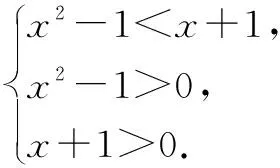
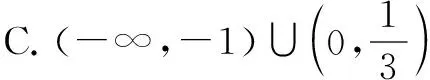
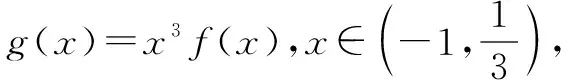
三、构造商函数
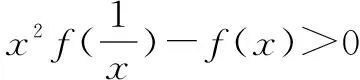
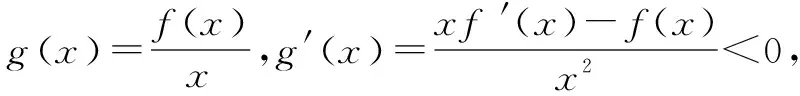
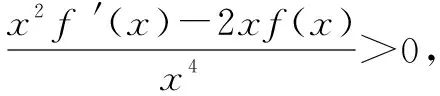
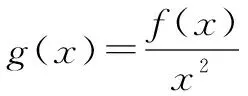
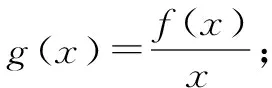
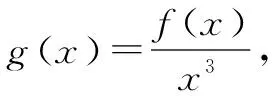
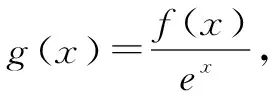
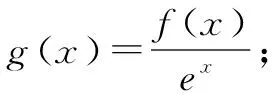
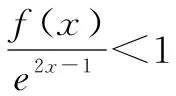
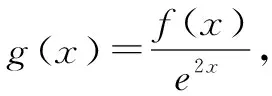
四、构造混合型函数