小学生数学学习力培养策略

【摘要】本文论述小学生数学学习力培养的策略，建议从知识结构能力、方法关联能力、思想感受能力和逻辑思维能力四个方面，培养学生的数学学习力，有效提升学生的数学核心素养。

【关键词】小学数学 学习力 培养

学习力是指一个人对知识信息的高效获取、整合转化和创新的能力。为了在数学课堂教学中有的放矢，加强学生学习力的培养，笔者通过观察法、访谈法、问卷调查法等方式，针对我校中高级段500名学生进行调查，发现学生存在在数学学习中看似理解了数学知识，实际上对概念的掌握并不准确;在解决数学问题时逻辑思维能力发展不足，在審题和分析问题方面能力比较薄弱等现象。很多学生学习了数学知识，却不知道如何应用到生活中，甚至没有建立起应用数学的意识，原因在于学生对所学知识缺乏系统的认知，在学习过程中缺乏深度探究和深度反思，导致对所学知识缺乏理性洞察力。由此可见，学生在数学学习力的四个方面（知识结构能力、方法关联能力、思想感受能力、逻辑思维能力）存在一定的缺陷，这正是教师在课堂教学中需要着重加强的部分。以下，笔者结合教学中实践，谈一谈在课堂教学中培养学生数学学习力的策略。

一、建构整体，注重知识结构能力的培养

数学教材大多按照总—分—总的顺序编排知识，但在实际教学中，大部分教师先让学生掌握一个个知识点，再把这些知识点串联起来，形成知识网络。这样的教学缺乏整体架构，学生所学过于零碎，对这些知识点“知其然，却不知其所以然”。这就需要教师改变原有的教学方式，摒弃教学零碎知识点的单一模式，从整体知识结构出发过渡到局部的知识点，激发学生数学学习的积极性，让学生的认知更富有深度。比如，在教学部编版数学五年级下册《长方体的体积》一课时，教师通常先让学生动手拼摆单位体积相等的两个小正方形木块，而后引导学生进行公式推导，得出长方体的体积公式。但笔者在教学中没有让学生将思维聚焦于推导长方体的体积公式，而是启发学生思考：想一想，长乘宽是计算长方体的什么？你还能找出计算长方体体积的方法吗？设置这个问题的目的在于启发学生构建长方形体积计算的一般结构。学生经过思考得出的结论：长方体的体积还可以用底面积乘高来计算。与此同时，学生自然而然推导出正方体的体积，即底面积乘高。这是一个“教结构”的过程，让学生牢固掌握了体积计算的方法。

在后续学习《圆柱的体积》时，笔者引导学生运用这一范式结构进行思考：想一想，长方体的体积是怎么计算的？圆柱体的体积也可以这样计算吗？学生在前期的学习中已经建立了体积计算的知识结构，基于此，就能够顺利推测出圆柱的体积等于底面积乘高。紧接着，笔者再次引导学生将已有的长方体、正方体、圆柱体的体积计算公式，类推直柱体的体积计算方法。通过“用结构”的方式，学生根据逻辑推理顺利地推导出直柱体的体积计算公式。

以上教学环节，教师着力于培养学生知识结构能力，让学生在掌握知识精髓和脉络的基础上“学结构”，进行知识的主动建构，再“用结构”进行知识创新，以获得新的知识结构。通过学结构—用结构—创结构的课堂教学，学生发现盘根错节的知识并不是零碎的片段，而是一个有机关联的整体，通过上下关联、前后贯通，学生由此建立了有深度的数学认知，实现数学学习力的迁移。

二、举一反三，注重方法关联能力的培养

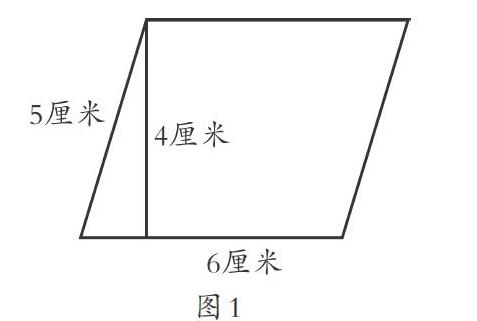
在数学学习中，学生学习力突出的表现就是能够进行方法的迁移。方法迁移来自学生对数学知识的三种理解，即工具性理解、关系性理解、结构性理解。教师要简化知识关联，举一反三，带领学生对知识内容进行深度探究，在实际操作中获得对知识方法的理解，顺利完成从知识的迁移到方法的迁移，发展学生的方法关联能力。比如，在教学《平行四边形的面积》一课时，笔者先出示一个平行四边形（如图1），让学生猜想面积的计算方法。

学生形成两种不同的意见。一种认为用6×4计算，即底边乘高;另一种认为用6×5进行计算，即底边乘邻边。对此，笔者引导学生进行验证，先是采用方格纸逐格计算的方法，但学生发现这个方法比较麻烦，为此他们继续寻找更为简单的方法。为了促进学生探究，唤醒学生的割补经验，笔者为学生出示图2，让学生计算图2的面积，从中找到计算面积的经验，并引导学生思考：这个面积计算的方法是什么？你能够将它运用在平行四边形的面积计算中吗？

这个简单的练习题让学生意识到，可以用割补法进行猜想验证，并提出将平行四边形转换成已经学过的图形，学生由此展开自由探索，形成多种不同的割补法。有的学生将平行四边形分割成一个直角三角形和一个直角梯形，也有的学生将平行四边形分割成两个直角梯形，还有的学生将平行四边形分割成两个三角形和一个长方形，再进行拼接。通过割补的方法，学生顺利地将平行四边形转化为长方形，从而推导出平行四边形的面积。

以上环节，教师用一道简单的面积计算题激活学生的割补经验，举一反三，引导学生建立方法关联，使学生站在知识结构、知识体系的层面多角度思考问题，并将此类问题进行分析及方法迁移，激活了学生的数学思维，彰显了学生数学学习力的发展。

三、创设情境，关注思想感受能力的培养

小学数学教学蕴含着丰富的数学思想，教师需要积极挖掘教材，在教学中创设情境，引导学生不但思考是什么，更要思考为什么，由此感悟数学知识背后的思维方法，对纷繁复杂的数学知识进行深度理解。以函数的思想为例，要让学生认识到一个量的变化，另一个量也随着变化，这两种量之间是对应的关系。这个函数思想就渗透在《用字母表示数》的知识内容中。笔者在教学中设计教学情境，运用一个小小的魔盒作为突破口，通过从“魔盒一端输入一个数，魔盒的另一端就会相应地出现另外一个数字”这样特定的情境，展示了对应的数学关系。至此，学生直观地感受到两种量的相互关联，“触摸”到了函数思想的内核。在这个过程中，笔者引导学生对两组数据进行观察，分析前后两组输入和输出数据的变化，学生由此认识到，使用字母时不但可以表示已知数，还可以拿来表示一些未知数以及变化中的数。通过这一课堂的探究，学生直观地认识到两种变量的依存关系，感受和体验函数思想的直观变化过程，为后续学习正反比例关系奠定坚实的基础。

以上环节，教师立足于学生思想感受能力的培养，引导学生从思维层面与知识发生碰撞，让学生主动探究数学知识，从中获得思想感悟。

四、善引问题，关注逻辑思维能力的培养

逻辑思维能力是学生数学学习力的核心，学生的一切学习活动都是在思维转换下完成。在小学数学教学中，逻辑思维力包括概括力、抽象力、连贯力等。教师要善于提出问题，大力发掘数学知识蕴含的育人功能，一方面引导学生在横向的知识结构进行关联，另一方面引导学生深入纵向知识结构进行拓展，帮助学生建构一个有序、有向的思维之网，培养和发展逻辑思维能力。比如，在教学《解决问题的策略——假设》时，有这样一道练习题：1个大盒子和5个小盒子里装满了球，一共80个球。其中，每个大盒子比小盒子多装了8个，求每个大盒子和小盒子各装多少个球？针对这一练习题，笔者从解决问题的策略入手，设计如下问题引导学生进行思考：你设想在什么盒子里装满球？根据你的假设，盒子里一共装了多少个球？要将什么盒子进行替换？替换后的盒子总数发生了什么改变？说说你的原因。替换之后，盒子总共有多少个？这些问题让学生对假设的数学策略形成理性洞察，从而建构一个有序的思维网络：为什么运用假设策略？怎么运用假设策略？在这个过程中，学生一步步学会从“为什么”到“怎么用”，逐步展开富有逻辑的数学思考。这样的数学思考，既有关系联想的发散思维，也有关系推理的聚合思维，不但提升思维的深度，也拓展了思维的广度。

以上环节，教师着力发展学生的逻辑思维能力，充分发掘知识背后的思维力量，从知识内容出发设计富有逻辑思维层次的问题引领，带领学生一步步前行，逐步发展学生分析问题和解决问题的能力，进而提升学生的逻辑思维能力。

在小学数学教学中，学习力的发展是学生个体自我超越、自我提升的过程。教师要基于学生的知识、能力、需求等个体特性，带领学生对知识进行探究和反思，加深对知识的认知。对学生数学学习力的培育，有助于学生深刻感受和领悟数学思想，内化数学知识、数学方法和技巧。经过长期、系统的训练，学生逐步将数学学习力转化为应用力和创新力，有效提升数学核心素养。

【参考文献】

[1]刘海玲.指向“下一次”的数学教学——提升儿童数学学习力的教学策略探寻[J].江蘇教育，2015（21）

[2]徐象党.浅谈学生数学学习力的培养[J].小学数学教育，2017（17）

[3]李瑾.关注过程，提升儿童数学学习力——以“用转化的策略解决实际问题”教学为例[J].小学教学参考，2018（26）

[4]金春平.如何培养小学生的数学学习动机[J].上海教育科研，2011（2）

[5]龚慧娟.指导·启发·帮助·激励——提升低年级学生数学学习力的策略[J].江苏教育学院学报（自然科学版），2011（1）

作者简介：覃海波（1977— ），女，广西兴业人，大学本科学历，一级教师，主要研究方向为小学数学教育。

（责编 杨 春）