Formation flight of fixed-wing UAV swarms:A group-based hierarchical approach

Hao CHEN, Xiangke WANG, Lincheng SHEN, Yirui CONG

College of Intelligence Science and Technology, National University of Defense Technology, Changsha 410073, China

KEYWORDS Control input constraints;Coordinated path following;Formation control;Leader-following control;Unmanned aerial vehicles swarms

Abstract This paper investigates a formation control problem of fixed-wing Unmanned Aerial Vehicle(UAV)swarms.A group-based hierarchical architecture is established among the UAVs,which decomposes all the UAVs into several distinct and non-overlapping groups.In each group,the UAVs form hierarchies with one UAV selected as the group leader.All group leaders execute coordinated path following to cooperatively handle the mission process among different groups,and the remaining followers track their direct leaders to achieve the inner-group coordination.More specifically,for a group leader,a virtual target moving along its desired path is assigned for the UAV,and an updating law is proposed to coordinate all the group leaders’virtual targets;for a follower UAV,the distributed leader-following formation control law is proposed to make the follower’s heading angle coincide with its direct leader,while keeping the desired relative position with respect to its direct leader.The proposed control law guarantees the globally asymptotic stability of the whole closed-loop swarm system under the control input constraints of fixed-wing UAVs. Theoretical proofs and numerical simulations are provided,which corroborate the effectiveness of the proposed method.

1. Introduction

1.1. Motivation

Autonomous Unmanned Aerial Vehicle (UAV) swarms have emerged as a disruptive technology for their enhanced flexibility and robustness compared to a single vehicle.1–4In this paper, we target at the formation flight of fixed-wing UAV swarms, which have broad application prospects due to the long range and endurance of these platforms.5–7Although significant achievements have been reported in recent years (see Section 1.2),much work remains to be done to bridge the technological gaps and make the system applicable in more civil and military scenarios. The motivation of this paper stems from the following three aspects:

(1) In real applications, a swarm of UAVs are expected to accomplish complicated missions, which usually can be divided into several parallel subtasks, e.g., the multitarget search or tracking scenario.8,9In these cases, the UAVs need to be decomposed into several distinct and non-overlapping clusters/groups, with each cluster/group carrying out one subtask,while different clusters/groups are also required to coordinate as a whole.Although there has been extensive research on coordinated control, most of the existing results only focus on the coordination within one cluster/group.

(2) Currently,a common approach to achieve actual formation flight of UAV swarms is to pre-plan a path or a trajectory for each UAV in the swarm,5,10,11which calls for coordinated planning. Coordinated planning produces paths/trajectories avoiding obstacles and inter-UAV collision,while optimizing the mobility of the UAV swarm,minimizing the energy consumption, etc.3Coordinated planning involves a number of parameters, and when the number of UAVs grows up, it would be a challenging task to produce so many paths or trajectories within limited amount of time.1,2

(3) Fixed-wing UAVs are less maneuverable compared to their rotary-wing counterparts.5,6,12To be more precise,a fixed-wing UAV is constrained not only by the maximum forward speed and heading rate,but also by a minimum positive forward speed to support itself during the flight. These control input constraints bring additional challenges to the coordination of UAV swarms, since many traditional methods proposed in the reference,such as Ref.13, cannot guarantee these constraints to be satisfied.If the control input constraints are not properly handled, the stability of the whole closed-loop swarm system would be influenced.

Therefore, it is necessary to develop efficient coordinated control methods satisfying the fixed-wing UAVs’control input constraints,and achieve coordination not only within the same group, but also among different groups in the swarm. In this paper, we focus on a group-based hierarchical approach to control fixed-wing UAV swarms, which can effectively handle the problems arising from the above three aspects.

1.2. Related work

Developing a swarm of UAVs has become a hot research topic in recent years.Nowadays,most of the UAV swarms reported are developed with rotary-wing drones. Industrial companies including Intel1https://www.intel.com/content/www/us/en/technology-innovation/aerial-technology-light-show.html, EHang2http://www.ehang.com/news/249.html, High Great3http://droneshow.hg-fly.com/en/, etc., have performed light shows with swarms of more than one thousand UAVs.However,it is believed that these UAVs are programmed with predefined trajectories or centrally controlled.10In academic field, distributed formation control problem has been investigated by many researchers, and readers are referred to Refs.14–16for surveys of existing methods. Several typical approaches including displacement based control,17distance based control18,19and bearing based control,20etc, have been studied with rotary-wing UAV formations. In most of these works, all the UAVs coordinate in a single common group.In contrast, a swarm of twenty quadrotors were divided into several groups in Ref.21, where the inter-group coordination is distributed, but the inner-group coordination is centralized.

Compared with rotary-wing UAVs, research on formation control of fixed-wing UAV swarms has received less attention.A vision-based leader-follower control method was proposed in Ref.22and validated by two UAVs, where a leader UAV is flying along the pre-planned path,and the follower UAV follows the leader by employing the onboard sensor measurements to obtain the relative states between two UAVs. Ref.23addressed the problem of driving multiple fixed-wing UAVs with non-identical constant forward speeds to reach stable circular motions,while their motion centers converge a particular formation shape. In Ref.24, a novel approach, termed guidance-route based formation control method was proposed, which generates guidance commands for fixed-wing UAVs by designing guidance-route generation strategies. As a great advance in terms of the scale, live-fly of fifty fixedwing UAVs was presented in Ref.25. Unfortunately, details of the control law were not provided in this work.We note that these works did not fully consider the fixed-wing UAVs’ control input constraints, which is one of the main difficulties in controlling fixed-wing UAV swarms.12,26,27Since the fixedwing UAVs are constrained by positive minimum positive forward speed, during the coordination process, a UAV cannot stop or become unacceptably slow to wait for another UAV.Besides, the heading rate and the forward speed are both with saturation constraints. Stability of the swarm needs to be investigated while meeting these constraints.In Ref.28,a trajectory tracking control law was proposed,which satisfies a fixedwing UAV’s control input constraints.Based on this,a leaderfollower formation control law was proposed in Ref.29for a group of followers to track a common leader.

Besides the above methods,another common way to achieve UAV formation flight is coordinated path following.Instead of tracking time-parameterized trajectories,the UAVs in the coordinated path following scenario follow geometric paths while trying to coordinate on some certain variables. Since a path need not be time-parameterized,it is more flexible to represent a path than to represent a trajectory.Several works in the literature discussed the coordinated path following control of fixedwing UAVs. In Ref.11, a coordinated path following control law was proposed to drive the UAVs to arrive at their respective destinations simultaneously. In Ref.12,the UAVs are expected to maintain the desired along-path separations while following a common path.The coordinated moving path following problem was introduced in Ref.27,where the desired path is moving on a plane.These works have considered some types of the control input constraints of fixed-wing UAVs. The minimum and maximum forward speed constraints were taken into account in all of these works,and the method in Ref.12even considered the heading rate constraints.However,in Ref.12,only local stability is guaranteed for the closed-loop of the coordinated path following system,when all the constraints of fixed-wing UAVs are considered. A major requirement associated with coordinated path following is that each UAV needs to have access to a pre-planned path, which would be a challenging task to plan many paths for coordinated planning as the number of UAVs increases.

1.3. Contributions

The above related work motivates the research in this paper to deal with the formation flight of multiple groups of fixed-wing UAVs subject to control input constraints.The main contributions of this paper are summarized as follows:

(1) We propose a distributed and scalable group-based hierarchical control architecture for swarms of fixed-wing UAVs, and achieve both the inter-group coordination and inner-group coordination.With the proposed architecture,we do not need to plan paths for all the UAVs in the swarm, and thus reduce the complexity of coordinated planning.

(2) We propose the formation control law for leader UAVs and follower UAVs in each group,respectively.The proposed control law guarantees the globally asymptotic stability of the whole fixed-wing UAV swarm even with control input constraints. Numerical simulations demonstrate the effectiveness of the proposed method.

1.4. Paper organization

The remainder of this paper is organized as follows. Section 2 formulates the coordination problem of fixed-wing UAV swarms and presents the group-based hierarchical architecture.Section 3 proposes the distributed control law for the UAVs in the swarm. Simulations are presented in Section 4 to corroborate the theoretical results. Finally, concluding remarks are summarized in Section 5.

2. Problem formulation and architecture design

In this section,we formulate the problem of formation flight of fixed-wing UAV swarms,present our group-based hierarchical architecture,and obtain the error dynamics of the system.The UAVs employed in this paper are all homogeneous.

2.1. Problem statement

To fulfill a complicated mission, the fixed-wing UAVs sometimes need to be decomposed into several distinct and nonoverlapping clusters, with each cluster executing a subtask.Besides, different clusters can merge into a common cluster according to the mission specification.Thus,the UAV swarms can form time-varying formation patterns during the flight.30As shown in the example in Fig.1,in Stage I,the whole swarm are divided into two clusters, with each cluster patrolling in a designated area; and in Stage II, these two clusters merge into a common larger cluster to continue the mission process. To accomplish the whole mission,not only the UAVs in each cluster are required to reach a specific geometric formation pattern to carry out a subtask, but also the different clusters need to coordinate their schedule such that all the UAVs can merge into a common cluster at the desired place.

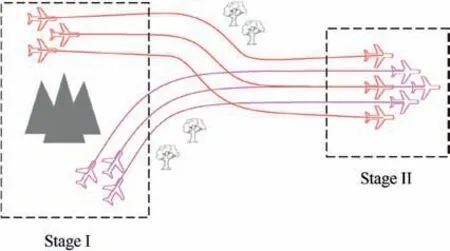
Fig. 1 Example of UAVs accomplishing a mission in several distinct and non-overlapping groups.

In many scenarios, the UAVs are flying at a constant altitude,27,31,32and we suppose each UAV has an independent altitude hold controller in its autopilot to hold the altitude constant. In that case, similar to Refs.12,32, the movement of a fixed-wing UAV on 2D plane can be represented as:

where vminand vmaxare the minimum and maximum forward speeds of the UAV,respectively,ωmaxis the maximum heading rate. For fixed-wing UAVs, the positive minimum forward speed vminis necessary to guarantee sufficiently large lift to support the UAV during the flight, the maximum forward speed vmaxresults from the finite actuation power of the throttle,and the maximum heading rate ωmaxis caused by the boundedness of the roll angle to ensure safety of the UAV.

With the above formulations, the problem of coordinating fixed-wing UAV swarms can be formulated as follows:

Problem 1. Consider a swarm of fixed-wing UAVs in several clusters, and the kinematic model of each UAV is represented by Eq. (1) with constraints inequality (2). Design control scheme such that any two UAVs in the same cluster maintain the desired relative positions, and any two clusters in the swarm can merge into a common cluster when necessary.

2.2. Group-based hierarchical architecture

Hierarchical architecture provides an efficient tool to deal with complex systems.33–35In this architecture, all the UAVs are organized in several distinctive labeled groups,each group corresponds to a small cluster which will not be further decomposed during the mission execution process. By employing the group-based structure,we let the UAVs in the same group work together to complete the same subtask of a complicated mission. In each group, one UAV is selected as the group leader,and the other UAVs in the group are called followers as a whole.The UAVs in the same group form a tree topology with the group leader UAV as the root. Fig. 2 shows the groupbased hierarchical architecture of n layers, consisting of one group leader layer,and n–1 follower layers.The group leaders communicate with each other to cooperatively handle the whole mission process, and they are also responsible for sending commands to their followers when necessary. The other UAVs except the group leaders each has one neighbor, which can be regarded as this UAV’s direct leader.The followers can obtain their direct leaders’ states through communication or sensing,and they use their direct leaders’states and commands to coordinate with their direct leaders.

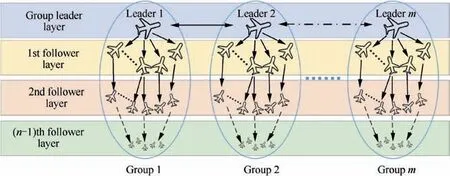
Fig. 2 Group-based hierarchical architecture of UAV swarms.

Based on the architecture shown in Fig.2,when performing a mission,we first use coordinated planning methods to generate a series of paths for the group leaders to follow; then we design coordinated path following controllers to coordinate the group leaders, and distributed leader-following formation controllers to coordinate the other UAVs with respect to their direct leaders. Since the underlying network of the swarm is finite, if the UAVs in the group leader layer are coordinated,and the UAVs in the follower layers are coordinated with their direct leaders, then the whole swarm is well coordinated.

Before going on,we make some brief comments on the proposed architecture. Its main benefits can be summarized as follows:

(1) The proposed architecture is distributed,and we even do not need a global observer as in Ref.36to provide the global information of the UAV swarms. Therefore, it exploits parallelism and is suitable to handle largescale swarms.

(2) Instead of making all the UAVs tightly coupled in an allto-all communication network, the proposed architecture reduces the communication bandwidth, since only one UAV in each group, i.e., the group leader, needs to communicate with the UAVs in the other groups.Besides, the other UAVs except the group leaders only need the information from one UAV, i.e., the UAV’s direct leader.

(3) In contrast to the approaches in Refs.11,37where all the UAVs need pre-planned paths to follow, the proposed architecture reduces the complexity of mission planning since the group leaders have the ability to guide the behaviors of the UAVs within the same group. As a result,we only need to plan paths for the group leaders.For the other UAVs, we can design distributed leaderfollowing formation controllers to yield the desired formation patterns.Since the proposed architecture reduces the complexity of coordinated planning,it can be scaled to handle larger swarms of UAVs.

(4) In contrast to the leaderless self-organization process discussed in the swarm robotics community,10,38the proposed architecture provides guarantees on the formation pattern and rigidity of the structure.As a result,it would be easier to predict the motion of each UAV, and thus facilitate human operators monitoring the whole mission process.

Remark 1. It is assumed that the UAVs are equipped with onboard sensors to detect potential conflicts, and the cooperative conflict resolution approaches such as Ref.31can be employed when necessary. In this paper, we do not consider conflict resolution in the problem setup.

For notational convenience, we use L to denote the set of group leader UAVs, and Fito denote the set of UAVs whose direct leader is the ith UAV.

2.3. Error dynamics

Based on the architecture in Section 2.2, the coordination of the whole swarm is twofold, i.e., the coordination of UAVs in the group leader layer, which corresponds to the intergroup coordination,and coordination of UAVs in the follower layers with respect to their direct leaders,which corresponds to the inner-group coordination. We discuss these two types of coordination one by one.

To coordinate the group leaders, we first use coordinated planning methods to generate a set of paths, and each group leader has a path to follow. Coordinated planning methods are out of the scope of this paper, and readers are referred to surveys in Refs.39,40. We assume that each path is globally known to the group leader that the path is assigned to. After generating the paths for the group leaders, we let these UAVs execute coordinated path following, instead of trajectory tracking as discussed in Ref.28. This consideration stems from two main reasons.Firstly, it is more convenient to represent a geometric path than to describe a time-parameterized trajectory. Secondly, the group leaders are most critical in the adopted architecture, and thus it calls for more robust strategies. Coordinated path following control is generally favored by researchers to yield this kind of robustness, since it is proven in Ref.41that trajectory tracking has fundamental performance limitations in the presence of unstable zero dynamics.Moreover, the performances of trajectory tracking are even worse in wind.26,31

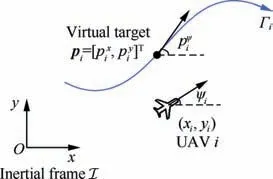
Fig. 3 Path following of a single group leader UAV i with its virtual target.

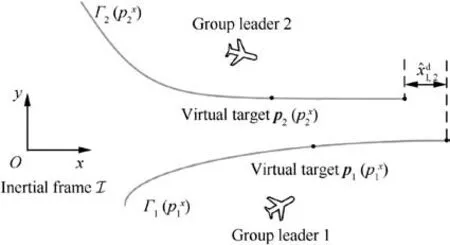
Fig. 4 An example to illustrate the coordinated path following of two group leader UAVs.

We use an undirected network GL=（VL，EL） to model the interaction among the group leaders,where VLis the set of vertices corresponding to the group leader set L,and ELis the set of edges, with each edge modeling a peer-to-peer interaction among the group leaders. The ith group leader UAV’s neighbor set Niis the set of group leaders that are connected to i by an edge.Based on the above analysis,the coordinated path following control for the group leader UAVs can be described as follows:

Problem 2. Consider a set of |L| group leader UAVs modeled by Eqs. (1) and (2) under Assumption 1. Given an undirected network GL=（VL，EL）,find a control law for i ∈L in the form of

Now we discuss the coordination control of follower UAVs with respect to their direct leaders, which is the inner-group coordination. Generally, in each cluster, the UAVs are required to maintain a geometric formation pattern during the formation flight.8Thus, the objective of controlling a follower UAV is to let its heading angle coincide with its direct leader, while keeping the desired relative position with respect to its direct leader. It is assumed that each follower knows its direct leader’s states, including the position, heading angle,and the control inputs. Therefore, the follower control problem can be formulated as follows:

Problem 3. Find a control law for a follower UAV i （i ∈Fl）modeled by Eqs. (1) and (2) in the form of

Remark 3. If Problem 2 is solved, it means the group leaders are well coordinated; and if Problem 3 is solved, it means the UAVs in each group are well coordinated.Therefore,with the group-based hierarchical architecture, if Problem 2 and Problem 3 are solved together, then Problem 1 is solved.

3. Control law design

In this section,we present the control law design in three steps.Firstly, a tracking control law considering the control input constraints of fixed-wing UAVs is presented, which will later be utilized by both the group leaders and the followers. Secondly, an updating law is proposed to coordinate the group leaders’ virtual targets. Based on these results, we finally specify the control law for each type of UAVs.

3.1. Tracking control law design

By comparing Eqs.(4)and(6),it can be found that they are in a similar form:the group leaders are tracking their virtual targets, which are moving on their respective paths, and the followers are tracking their direct leaders. Therefore, we design a common tracking control law which can be employed by both types of UAVs, and the tracking problem is formulated as follows:

To solve Problem 4,we first represent the tracking errors in the ith UAV’s body frame by using the following coordinate transformation, as shown in Fig. 5.

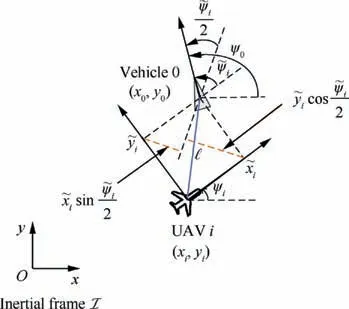
Fig. 5 Illustration of the tracking control.

The following lemma states that the tracking problem can be solved by properly selecting parameters k1, k2, and k3.

3.2. Updating law for group leaders’ virtual targets

where wij=wji>0, γd，γ+>0 and γd-γ+>0, the saturation function z=Sat（x，a，b）:R →R, where ab;and z=x otherwise.The following lemma states that the virtual targets of the group leaders can be coordinated with the updating laws (17)–(18).

3.3. Control law for each type of UAVs

With the above results in Sections 3.1 and 3.2,we are now able to specify the control law for each type of UAVs.

For group leaders,they are tracking the virtual targets that are moving on their respective paths. The movement of a virtual target follows the updating law (17)-(18). Based on the tracking control law (13)-(14), the control law for i ∈L in the form of Eq. (4) is designed as:

The stability of the follower control closed-loop is summarized as the following theorem.

4. Simulation results

In this section,numerical simulations of a swarm of ten UAVs in a coordination mission are provided to corroborate the effectiveness of the proposed group-based hierarchical formation control method. The UAVs are divided into two groups,and each group contains five UAVs. UAV 1 and UAV 6 are selected as the group leaders, and UAVs 2–5 and 7–10 are as their followers, respectively. The UAVs are required to pass through narrow passages and achieve coordinated coverage of a target area. To fulfill this mission, we plan two paths,and each path is for a group leader to follow. The paths are produced by B-splines31that pass through predefined waypoints shown in Table 1. Thus, the signed curvature of each path is continuous, and satisfies |κ（θi）|<0.0064.

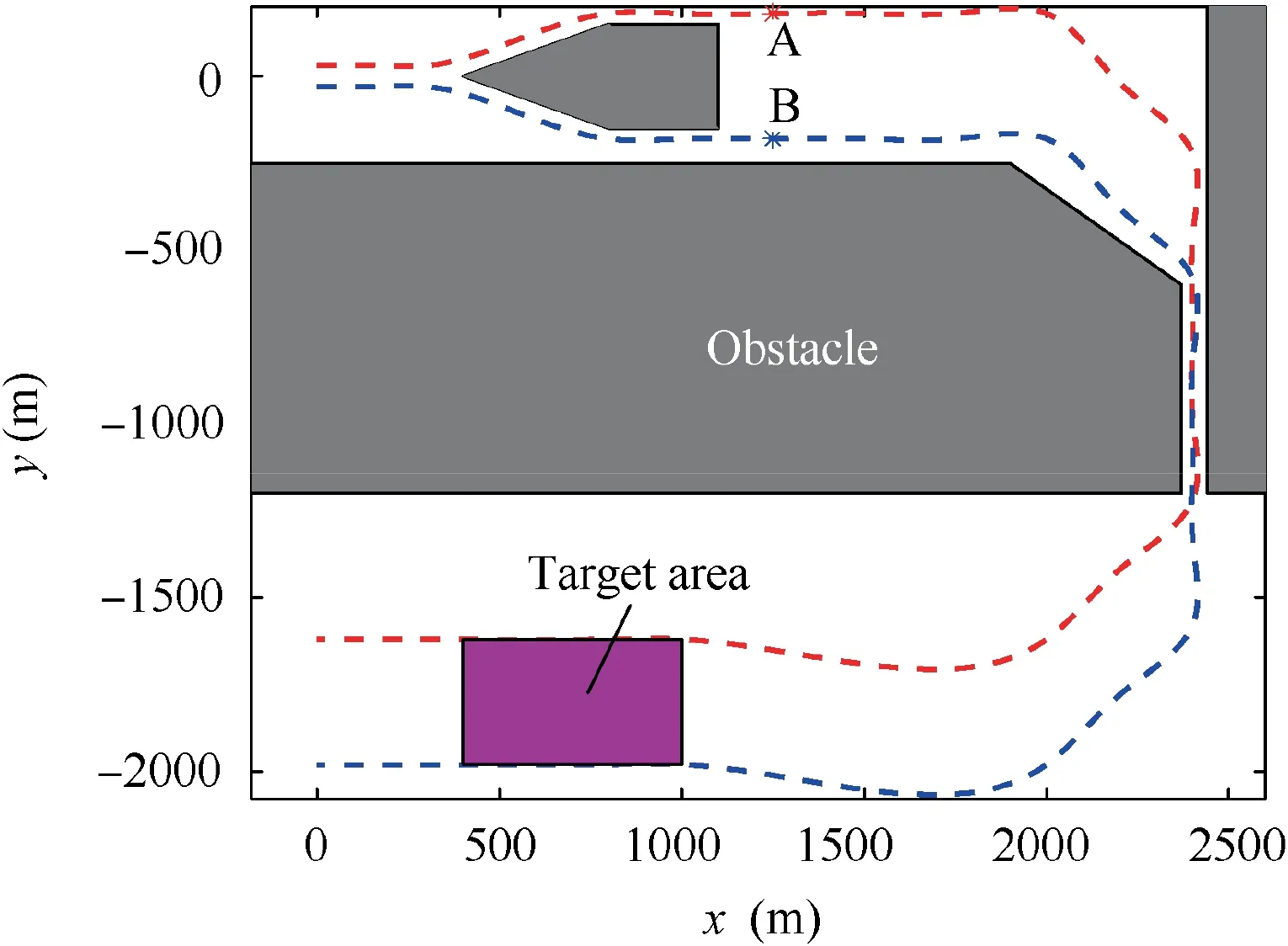
Fig. 6 Mission environment and the generated two paths for group leaders, UAV 1 and UAV 6.

The mission environment and the generated two paths are shown in Fig. 6. The two paths have equal path length, and the two group leaders aim to maintain the same path-length parameter when moving on their respective paths. Here the paths are parameterized with respect to the path-length parameter,i.e.,θi=si（i ∈L）,and thus the virtual targets’coordination objective is to achieve θ1-θ6→0 (i.e., s1-s6→0).Points A and B are two special points on the paths, corresponding to the 7th waypoints of the paths. Since the pathlength parameters of points A and B are the same, the two group leaders are expected to arrive at these two points simultaneously.After UAV 1 and UAV 6 get to points A and B,the formation pattern of the swarm will reconfigure, such that the whole swarm can pass through the new narrow passage and cover the target area in a coordinated manner. Table 2 shows the desired relative positions of the follower UAVs with respect to their group leaders before and after the formation pattern reconfiguration.

The control input constraints of the UAVs are vmin=10m/s, vmax=19m/s, and ωmax=0.56rad/s. Initial states of each UAV are listed in Table 3. The initial positions of the group leaders’ virtual targets are set as the closest projection points of the group leaders on their respective paths,and thus θ1（0）=34.78m, θ6（0）=15.84m.

Table 1 Positions of waypoints in each path.

Table 2 Desired relative positions of followers with respect to their group leaders.

Table 3 Initial states of each UAV.

Fig. 7 presents the formation flight results of the 10-UAV swarm.The desired paths for the two group leaders are shown in dashed lines,and the trajectories of all the UAVs are shown in solid lines. The wedges indicate the positions and headings of the UAVs. In Fig. 7(a), the UAVs form two clusters, and each cluster corresponds to one group of the proposed architecture. Fig. 7(b) shows the process of UAVs merging into one common cluster and the whole swarm forming a oneline formation pattern.Fig.7(c)shows the UAVs pass through a narrow passage in a line. The UAVs keeps this formation pattern to cover the target area in Fig. 7(d).

Fig. 7 Trajectories of all UAVs.

Fig. 8 Errors of each UAV during formation flight.

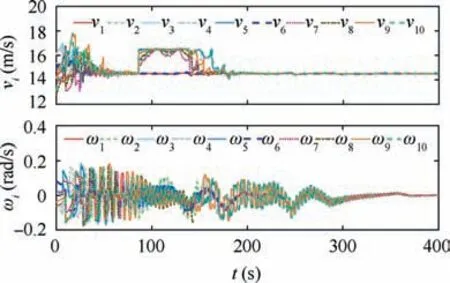
Fig. 9 Control inputs of each UAV during formation flight.

Fig. 10 Errors of each UAV in simulation with 5 layer architecture.

Fig. 10 shows the errors of each UAV in the simulation with the architecture consisting of 5 layers. Since the parameters for tracking become smaller due to the increase of number of layers in the architecture, it takes longer time for the tracking errors to converge to zero in Fig. 10 than in Fig. 8.

5. Conclusions

In this paper, we address the problem of formation flight of fixed-wing UAV swarms. The UAVs are organized in several distinct and non-overlapping groups, and form hierarchies in each group.There are two types of UAVs in the swarm,group leader UAVs and follower UAVs.We design coordinated path following control law for the group leader UAVs, to let these UAVs fly along their respective paths, while achieving intergroup coordination according to the mission specification.Besides, a leader-following formation control law is proposed for the follower UAVs to make these UAVs coordinate with their direct leaders.The proposed approach is distributed,scalable, and provide guarantees on formation patterns. Moreover, the globally asymptotic stability with the proposed method is guaranteed by properly selecting parameters.Results of theoretical analysis and numerical simulations indicate that the architecture with two layers is preferred, and demonstrate the effectiveness of the proposed method.

Future work includes the validation of the proposed method with actual fixed-wing UAV platforms, considering the limited-budget coordination,45wind disturbances, and three-dimensional formation control law.

Acknowledgements

This work was supported in part by National Natural Science Foundation of China (Nos. 61973309, 61801494 and 61702528), in part by Hunan Provincial Innovation Foundation for Postgraduate, China (No. CX2017B014).