Towards intelligent design optimization: Progress and challenge of design optimization theories and technologies for plastic forming

Heng LI, Jingho YANG, Gungyo CHEN, Xin LIU, Zho ZHANG,Gungjun LI, Wenhui LIU

a State Key Laboratory of Solidification Processing, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

b Chengdu Aircraft Industry (Group) Corporation Ltd., Chengdu 610092, China

c High Temperature Wear Resistant Materials and Preparation Technology of Hunan Province National Defence Science and Technology Laboratory, Hunan Provincial Key Laboratory of Advanced Materials for New Energy Storage and Conversion, School of Materials Science and Engineering, Hunan University of Science and Technology, Xiangtan 411201, China

KEYWORDS Advanced manufacturing;Design optimization;Deterministic optimization(DOP);Intelligent design optimization (IDO);Plastic forming;Uncertain optimization(UOP)

Abstract Plastic forming is one of enabling and fundamental technologies in advanced manufacturing chains.Design optimization is a critical way to improve the performance of the forming system, exploit the advantages of high productivity, high product quality, low production cost and short time to market and develop precise, accurate, green, and intelligent (smart) plastic forming technology.However,plastic forming is quite complicated,relating to multi-physics field coupling,multi-factor influence, multi-defect constraint, and triple nonlinear, etc., and the design optimization for plastic forming involves multi-objective, multi-parameter, multi-constraint, nonlinear,high-dimensionality, non-continuity, time-varying, and uncertainty, etc. Therefore, how to achieve accurate and efficient design optimization of products,equipment,tools/dies,and processing as well as materials characterization has always been the research frontier and focus in the field of engineering and manufacturing. In recent years, with the rapid development of computing science, data science and internet of things (IoT), the theories and technologies of design optimization have attracted more and more attention, and developed rapidly in forming process. Accordingly, this paper first introduced the framework of design optimization for plastic forming. Then, focusing on the key problems of design optimization, such as numerical model and optimization algorithm,this paper summarized the research progress on the development and application of the theories and technologies about design optimization in forming process, including deterministic and uncertain optimization. Moreover, the applicability of various modeling methods and optimization algorithms was elaborated in solving the design optimization problems of plastic forming.Finally,considering the development trends of forming technology, this paper discusses some challenges of design optimization that may need to be solved and faced in forming process.

Nomenclature

IoT internet of things

AI artificial intelligence

DOP deterministic optimization

UOP uncertain optimization

DOE design of experiment

IDO intelligent design optimization

FE finite element

MC Monte Carlo

RBDO reliability based design optimization

RDO robust design optimization

WCSBO worst case scenario based optimization

NPM non-probabilistic methods

SNR signal noise ratio

FDM finite difference method

CPM classical perturbation method

IPM iterative perturbation method

RSM response surface model

KM Kriging model

SVM support-vector machine

RBF radial basis function

GA genetic algorithm

ACO ant colony optimization

FA firefly algorithm

PSO particle swarm optimization

SQP sequential quadratic programming

SVDD singular value decomposition of degree

NSGA-II non-dominated sorting genetic algorithm II

LS-SVM least-squares support-vector machine

MLS moving least squares

BBD Box-Behnken design

ILLF isothermal local loading forming

ETB equal-thickness billet

UTB unequal-thickness billet

GSA gravitational search algorithm

HGSANM hybrid gravitational search-nelder mead algorithm

ANNCPFEM artificial neural networkcrystal plastic finite element model

KBS knowledge-based system

ILC iterative learning control

ANFIS adaptive neuro fuzzy inference system

DIP digital image processing

MFO model-free optimization

1. Introduction

Plastic forming is one of enabling and fundamental technologies in advanced manufacturing chains, and especially it is indispensable and critical for fabricating high-performance components widely applied in the high-end fields of aviation,aerospace, automobile and energy, etc.1It is characterized by comprehensively controlling the deformation process from blanks to final components, viz., obtaining the complex shape of components,modifying their microstructure and improving their mechanical properties, and finally realizing their integrated manufacturing with shape forming and properties tailoring.2As illustrated in Fig. 1, there are many factors determining the performance of the final components, process and the entire forming system in plastic forming process.3And these factors are closely to the mass production of the components fabricated by forming, which will inevitably bring it many challenges such as high productivity,high product quality,low production cost and short time to market,as shown in Fig. 2. Thus, it can be seen that design optimization is very essential and critical for plastic forming process.It is generally known that design optimization is the foundation to shorten the product manufacturing cycle, improve the forming limit and quality, realize the stable control of forming quality and bring the superiority of batch production into full play. However, plastic forming is a complex process with features of multi-physics field coupling, multi-factor influence, multidefect constraint, and triple nonlinear of material, geometry and boundary.Design optimization in forming process is usually faced with many numerical modeling and computation challenges such as multi-objective, multi-parameter, multiconstrain, nonlinear, high-dimensionality, non-continuity,time-varying, and uncertainty. In order to control the deformation process of forming accurately and robustly and realize energy saving and cost reduction in forming process, how to achieve accurate and efficient design optimization of products,equipment,dies,and process as well as materials characterization has always been the research frontier and focus in the field of engineering and manufacturing.4In particular, along with the demand of long life,low energy consumption and high efficiency in aviation and aerospace, in addition to the driving effect of new technologies such as computing science, data science, internet of things (IoT) and artificial intelligence (AI)towards green manufacturing and intelligent(smart)manufacturing under the economic globalization,it is urgent to develop accurate and efficient design optimization theory and technology for rapidly developing new products, new processes and new equipment, etc. This has become a common and critical issue to develop accurate, green, and intelligent forming technology.

Fig. 1 Factors affecting entire forming system in forming process.3

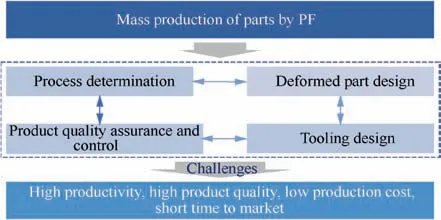
Fig. 2 Challenges of mass production of parts by forming.

Design optimization is widely applied and developed in many manufacturing fields such as casting, forming and welding. In the field of plastic forming, design optimization is needed from start to finish in the whole forming process,which endows it with the unique property.As we all know,trial-anderror is actually a rough design optimization method, and there are many kinds of design optimization methods based on various classification methods. For instance, design optimization can be classified into static optimization and dynamic optimization according to whether the optimization strategy is numerical or functional;functional optimization and combinatorial optimization according to whether the optimization object is continuous or discrete; unconstrained optimization and constrained optimization according to whether there is constraint or not; high-dimensional optimization and lowdimensional optimization according to the dimensions; deterministic optimization (DOP) and uncertain optimization(UOP) according to whether the design variable considers the uncertainty. Essentially, design optimization is a mathematical method, viz., based on the mathematical optimization theory and by means of computer, the objective function is established according to the optimization objective pursued by the design, then under the given constraints, the optimization algorithm is used to find the optimal design case, such as the best technical and economic indexes of good performance and low cost. With the development of connotation and extension of forming technology, design optimization is widely used in many scenarios such as inverse calibration of constitutive parameters,forming mechanism analysis,perform design, process parameter design and tool/die parameter optimization, etc.; with the rapid development of computer hardware and software, the research of design optimization for plastic forming has experienced the process from design of experiment(DOE),analytical method to numerical simulation,and the design optimization calculation includes complex numerical models such as meta model and various optimization algorithms such as intelligent design optimization (IDO)algorithm.5–16As a result, many related commercial software and open sharing algorithms have been developed. Focusing on the forming process characteristics and aiming at balance between efficiency and precision, many scholars have carried out a lot of research on multi-objective and nonlinear design optimization. However, most studies are limited to a specific algorithm in a certain process, and there are few systematic reviews on the design optimization methods and approaches for forming process.

According to the above analysis,it is essential to summarize the research progress and challenge of design optimization theories and technologies for plastic forming. Firstly, the framework of design optimization for forming is introduced. Then,focusing on numerical models and optimization algorithms for DOP and UOP, this paper summarizes the research development and application of design optimization theories and technologies in forming process. From aspects of accuracy and efficiency, the applicability of various modeling methods and optimization algorithms in solving the design optimization problems of practical forming process is set forth. Eventually,considering the development trend of forming technology,this paper attempts to discuss some challenges of design optimization that may need to be solved in forming process.

2.State of art of theories and technologies of design optimization in plastic forming

The design optimization process is mainly divided into two key procedures: the establishment of the optimization model and the solution through the optimization algorithm. The key of the design optimization solution lies in the selection of accurate design variables, the establishment of efficient mapping models between variables and responses (evaluation models),and the selection of applicable optimization algorithm. There are three elements in the optimization models,i.e.,design variables, constraints and objective function: design variables can be continuous or discontinuous; constraints usually include equality and inequality constraints, linear and nonlinear constraints, or boundary constraints; objective functions can be explicit formula or implicit one. As shown in Fig. 3, in the design optimization process, the mapping models between variables and response are available through DOE, analytical models and finite element (FE) calculation. However, due to the limitations of DOE and FE calculation in efficiency and cost, it is often necessary to establish corresponding approximate response models based on the above sampling calculations, such as meta model (surrogate model), sensitivity analysis model,Monte Carlo(MC)analysis model,and Taguchi method, etc. After the above mathematical modeling of design optimization problem, the second stage of design optimization is to solve the established optimization model by applying the various kinds of optimization algorithms. The optimization algorithm needs to evaluate the response, i.e.,making the objective function converge to the optimal value by iteration. For many different types of optimization problems such as determinacy and uncertainty, a various of optimization algorithms have been developed, mainly including accurate algorithms (absolute optimal solutions) and heuristic algorithms(approximate algorithms),etc.The different combinations of the above response evaluation methods and optimization algorithms are suitable to different kinds of design optimization problems, and their accuracy and efficiency will also vary. Two kinds of design optimization problems i.e.,DOP and UOP, as well as corresponding response evaluation models and optimization algorithms, will be discussed in the following.

2.1. DOP and UOP

Traditionally,design optimization in forming process is mostly based on DOP methods,which means that the values of design variables, objective functions, and constraint functions are deterministic rather than fluctuant.7However, as shown in Fig. 4, in actual forming process, no matter controllable parameters or uncontrollable parameters i.e., noise factor, it is inevitable to generate uncertainties such as obvious dispersivity,randomness and volatility and their transfer phenomena among deformation materials,external energy,interacting surface and deformation process.These uncertainties may lead to process failure, tool damage, and uncertain of component quality and function,and thus seriously affecting the efficiency and accuracy of plastic processing and resulting in large reject rate and high manufacturing cost.7,17–31It is noted that these uncertainties in forming process are inherent and unavoidable,which often lead to the failure of the results of DOP.Thus,the optimization problem caused by the uncertainty in the forming process cannot be ignored. In view of the above uncertain problems in the forming process, by introducing the mathematical theories such as probability and statistics theory,fuzzy theory and interval analysis, and by continuously developing optimization algorithm and improving computer performance,the DOP has been extended to the optimization that considers the uncertainty of design variables,viz.,UOP.In recent years,the concept and method of uncertainty-based design have been developed and applied rapidly.

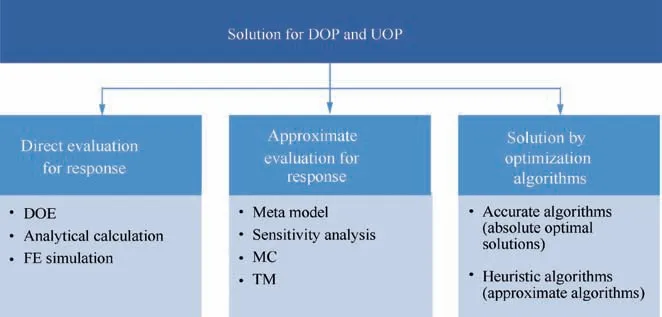
Fig. 3 Design optimization framework in forming process.

Fig. 4 Uncertainties in forming process.

The input uncertainty in forming process will result in the uncertainty of output or response f (including constraints),which means the response is a distribution not a definite value.The input can be divided into the controllable design variable x and the uncontrollable design parameter p. The uncertainty of design variables is caused by the limited degree of their controllable accuracy with unknown or known distributions. The typical cases are the material properties fluctuation, geometry changes such as material thickness, geometric tolerances of tools/dies, manufacturing deviation, and load variations in process such as temperature variation, friction boundary condition, processing pass, and initial setup. The uncertainty of the response f=f（x +Zx，p） can be calculated by considering the disturbance Zxof design variables. In most cases, the uncertain design variables are expressed by the average value and corresponding standard deviation. The uncertainty analysis answers the questions of what the distribution of system parameters is, i.e., average value, standard deviation or interval,and what the distribution of system performance is,generally referring to as system output that may be design objective or design constraint.

As shown in Table 1, in view of the above UOP problems,based on the DOP, reliability based design optimization(RBDO), robust design optimization (RDO), worst case scenario based optimization (WCSBO), and non-probabilistic methods (NPM) have been investigated and developed.18,19Under the premise that the probability distribution of input variables is known, both RBDO and RDO explicitly consider the probability distribution, but WCSBO and NPM turn the uncertainty problem into the certainty problem when the uncertainty of input distribution is cognitive or non-cognitive(accidental uncertainty or random uncertainty).

As shown in Fig. 5, focusing on the determination of the optimal solution of a certain objective function and ensuring that the product or production process fails with a predefined acceptable small probability, RBDO concentrates onthe ability of the product to perform the specified functions so as to reduce the reject rate and manufacturing cost; by minimizing the variance of the response, viz., narrowing the response range, RDO concentrates on the stability of product quality so as to reduce the sensibility of response to small change in uncertainty input and avoid the failure event under extreme conditions; WCSBO uses the minimax idea to maximize the minimum distance between the optimal and the failure constraint; NPM uses the interval models and fuzzy sets to describe the uncertainty, which is efficient in solving the optimization problem of unknown or unknown uncertainty.32,33It is noteworthy that some constraint formulas are supposed to be considered in the RDO problems, and the method based on robustness and reliability should be integrated into the reliable RDO problems. Additionally, when numerical techniques are used to describe the real physical process,the model’s uncertainty caused by numerical noise should be considered.34

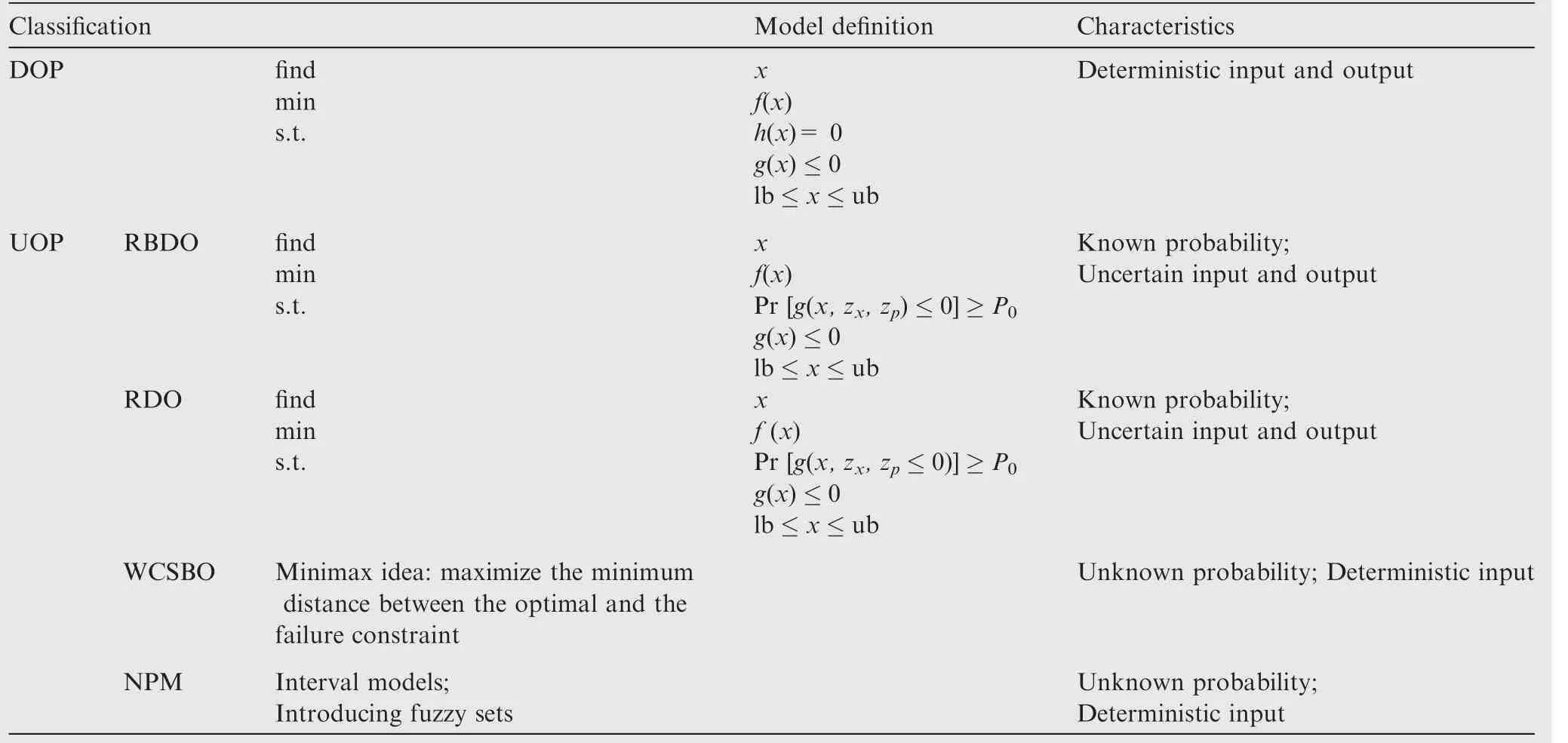
Table 1 Characteristics of DOP and UOP in design optimization for forming process.

2.2. Numerical modelling methods

As the above mentioned, if the physical experiments and the virtual experiments are carried out in the DOP, especially UOP, the computational cost for calculating the response(the objective function)will be extremely high,and it is difficult to calculate its gradient or derivative. Therefore, as shown in Fig.6,MC method,sensitivity analysis,Taguchi method,meta model and other numerical methods are developed to combine with reliability method for design optimization calculation.

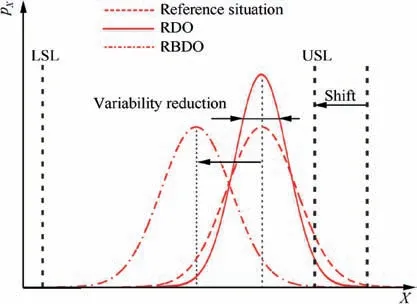
Fig. 5 RBDO and RDO.7

MC method,also known as statistical simulation method,is a general simulation technology, which is suitable for random analysis and sampling. Its theoretical basis is the law of large numbers and central limit theorem in probability theory. The basic principle of MC is to obtain the distribution of the corresponding function response of the random variable by using the random number generator and repeating independent direct or indirect sampling (simulation). When the simulation times are enough, the probability distribution of the response function Y, which is similar to the actual situation, and the information such as the number characteristics concerned can be obtained.The computational cost of direct MC method combined with FE method is so huge that a series of advanced MC methods have been developed, such as adaptive MC simulation, subset simulation, importance sampling and descriptive sampling.

Sensitivity analysis method is used to calculate the sensitivity of the response to the input variables, mainly including finite difference method(FDM),classical perturbation method(CPM)and iterative perturbation method(IPM).FDM is used to approximately calculate the response sensitivity of the input variables, and its basis is to calculate the effect of each disturbance of each variable on the response through multiple FE simulations. According to the way of variable perturbation,FDM is classified into forward difference method, backward difference method and central difference method. CPM and IPM are mainly applied to calculate the sensitivity of the objective function to the variation of random input variables.In the CPM, the change of response is estimated by considering the change of random input variables in each step of deterministic analysis; while in practice, the derivative of target response adopts the differential chain rule for multiple input variables,so it needs to use the iterative process to solve. The value of the above response function is obtained by deterministic FE analysis, and the gradient is obtained by FDM, CPM or IPM. This method is called stochastic FE method by combining FE analysis with probability analysis.The limitation of the sensitivity analysis methods such as FDM lies in the high calculation cost and the easy occurrence of truncation and roundoff errors.

Taguchi method is a RDO method proposed by Taguchi,which makes the quality of the designed product stable, the production process insensitive to various noise factors, and has little fluctuation.35The key of Taguchi method lies in the orthogonal DOE of internal and external tables, where the controllable factors are placed in the internal table and the noise factors are placed in the external table. Taguchi method uses signal noise ratio (SNR) as the evaluation index,and has different SNR calculation formulas for various quality characteristics. The response is optimized by maximizing the SNR to minimize the design change. Taguchi method is relatively simple,but it can’t separate the influence of controllable variable and noise factor on the mean value and variance of the response.

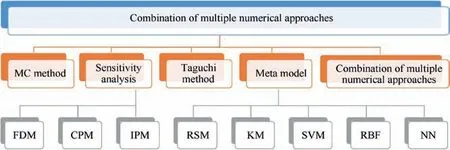
Fig. 6 Classification of numerical models in design optimization of forming process.

The main idea of meta model or surrogate model method is to construct the approximate mathematical model by sampling in the design space system,replace the experiment and simulation,and solve the problems of high cost of experiment and FE calculation and large amount of design optimization data.36The metal model mainly includes response surface model(RSM), Kriging model (KM), support-vector machine(SVM), radial basis function (RBF) model and neural networks (NN), etc. RSM is to use all kinds of data by physical and virtual test to fit the meta model,and generate polynomial regression function y=f（x1，x2，···，xn）:regarding the index y,i.e.,the response variable,as the function of experimental factors x1，x2，···，xn. The regression function could be regarded as a curved surface in geometric space,which is called response surface.37KM is an interpolation model whose interpolation result is defined as the linear weighting of the response value of the known sample function,and it has good approximation ability of nonlinear function and unique error estimation function.38–41RBF model is derived from the interpolation of scattered multivariate data, and it uses the linear combination of symmetric radial basis functions based on Euclidean distance to describe itself.42RBF model has been proved to fit deterministic and stochastic response functions well, and has been developed into adaptive RBF model to deal with global optimization problems.24NN algorithm can approach any functions in theory, and its basic structure is composed of nonlinear variable elements, which has strong nonlinear mapping ability. Due to high computational efficiency and easy to implement parallel computing, the above meta model method is a promising numerical method,and KM and RBF model are more suitable for highly nonlinear problems than RSM.However,it is noted that a FE model is an approximate model of a forming process, while meta model is an approximation of a FE model,so that leading to errors.Thus,the balance between the approximate accuracy and the complexity of the model should be considered. Usually, the design variables can be reduced by screening methods to overcome the ‘‘curse of dimensionality”.43

2.3. Design optimization algorithms

There are many features of design optimization in forming process, including multi-objective, multi-parameter, multiconstraint,and nonlinear,etc.As for these features,it is essential to combine the above numerical models with different optimization algorithms for solving the design optimization problems in forming process. As mentioned above, there are lots of optimization algorithms, for instance, functional optimization and combinatorial optimization algorithms, unconstrained optimization and constrained optimization algorithms,accurate algorithm(iterative algorithm or absolute optimal solution) and heuristic algorithms (approximate algorithm). As shown in Fig. 7, the classification of accurate algorithm and heuristic algorithm is based on whether to solve the derivative of different orders of the objective function. Accurate algorithm is a traditional optimization algorithm. By using the optimal solution obtained by the derivative information of the objective function iteratively, accurate algorithm can be subdivided into direct solution method without derivative information, gradient method with first derivative,Newton series method with second derivative, etc. Classical accurate algorithms include conjugate gradient algorithm,sequential quadratic programming and quasi Newton, etc.44Sensitivity analysis method is widely used to calculate the gradient of objective function.The optimization method based on sensitivity analysis belongs to gradient optimization method.The limitation of iterative algorithm is that it is easy to fall into local optimum, so it is usually called local algorithm. Moreover, the result of the solution by iterative algorithm depends on the initial value strongly.

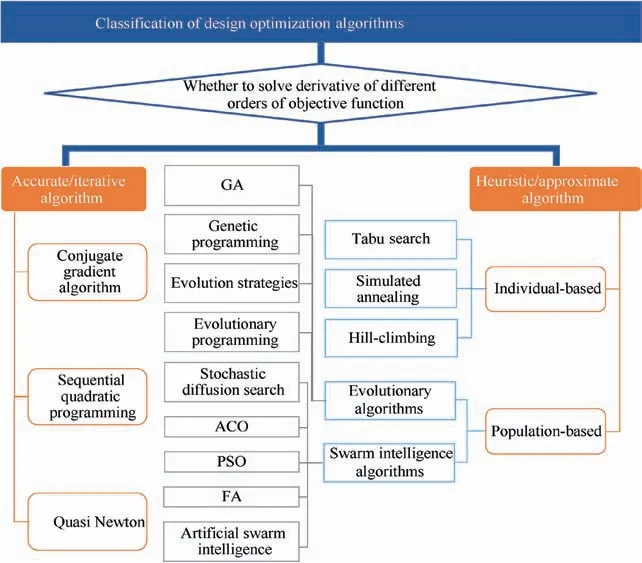
Fig. 7 Classification of design optimization algorithms.

As shown in Fig.5,heuristic algorithm refers to the method of finding the solution according to the rule-of-thumb when solving the problems, rather than the systematic and definite steps to find the answer.43To a certain extent, this kind of method can solve complex problems such as large space, nonlinear, global optimization, combinatorial optimization, etc.Heuristic algorithm is divided into individual-based heuristic algorithm, i.e., searching for relative optimum, and population-based heuristic algorithm,i.e.,searching for global optimum. Individual-based heuristic algorithms include hillclimbing (also known as local search), Tabu search and simulated annealing.Population-based heuristic algorithms contain evolutionary algorithms,artificial neural network(ANN)algorithms and swarm intelligence algorithms. It is noted that, in recent years, these algorithms have attracted more and more attention and been widely applied in the field of design optimization in forming process.The representative heuristic intelligent algorithms are briefly discussed as follows.

Simulated annealing algorithm, whose name and inspiration originate from annealing in metallurgy, is a stochastic optimization algorithm based on MC iterative solution strategy. Its origin is based on the similarity between annealing physical process and general combinatorial optimization problems.45–47Starting from a certain high initial temperature and going through the continuous decline of temperature, this algorithm randomly searches the global optimal solution of the objective function in the solution space in combination with the probability-sudden-jump characteristics. The local optimal solution can jump out and eventually tend to the global optimal solution.48–51However, it has several following shortcomings: 1)it has slow rate of convergence; 2)the global search ability is poor, it is easy to be affected by parameters,and the parameters are difficult to control;3)the approximate optimal solution is often found in practical application.This is because it has strict requirements on the conditions of finding the optimal solution, viz., the initial temperature should be high enough, the termination temperature should be low enough, and the cooling process should be slow enough.

Evolutionary algorithms are well known due to the mechanisms inspired by biological evolution, such as reproduction,mutation,recombination,and selection.52They mainly include genetic algorithm(GA),53,54genetic programming,55evolution strategies,56and evolutionary programming.57GA, the most popular type of evolutionary algorithms often used in optimization problems, is commonly applied to produce superior solutions for optimization and searching problems by depending on biology-inspired operators such as selection, crossover and mutation.58However, as for evolution strategies and evolutionary programming, their mechanisms of searching operators originate from mutation and selection by using natural problem-dependent representations.59GA and genetic programming emphasize the genetic chain of parents to offspring,while evolution strategies and evolutionary programming focus on the behavior properties of children themselves, i.e.,behavior chains.Evolutionary algorithms tend to find the global optimal solution and allow parallel computing without the gradient information of the function.60The drawbacks of GA are as follows:1)it has slow rate of convergence.In the process of evolution,crossover and mutation can’t guarantee the excellence of the new individuals. If the individuals are not good enough, they will slow down the convergence rate; 2) it has the problem of early maturation.Because GA only determines the solution according to the fitness function, the individuals with higher fitness spread rapidly in the population, which leads to the population losing diversity prematurely and falling into the local optimum; 3) the ability of local optimization is poor. The poor local optimization ability of GA leads to the slow convergence rate in the late evolution stage, and even can’t converge to the global optimal solution; 4) there are many design variables and there is no definite termination criterion.

The concept of swarm intelligence algorithm originates from the observation of insects and other groups in the nature.61The macro intelligent behavior characteristics of gregarious organism individuals through cooperation are named as swarm intelligence. Swarm intelligence algorithms include stochastic diffusion search,62,63ant colony optimization(ACO),64,65particle swarm optimization (PSO),66,67firefly algorithm (FA),68and artificial swarm intelligence,69etc.PSO was first proposed to simulate social behavior, for instance, the representative movement of organisms in a bird flock or fish school. Then it was simplified and developed to be a stochastic search algorithm based on group cooperation for optimizing a problem by iteratively attempting to improve a candidate solution about a given quality measure, whose advantage lies in simplicity, easy implementation and no adjustment of many parameters. PSO can be integrated into multi-agent optimization system.22,70–72Its shortages are as follows: 1) it is easy to fall into local extremum; 2) its search accuracy is not high;3)the efficient information sharing mechanism of PSO may lead to the excessive concentration of particles in the optimization process, which makes the particles move to a global optimum, so it can’t be used in multimodal function optimization; 4) when the PSO algorithm is used to solve optimization problems with discrete variables,the rounding of discrete variables may lead to large errors.

It is worth noting that DOE is the premise and foundation of design optimization. As a construction method, it determines the significant factors and establishes the relationship between the influence factors and the response,and thus establishing the agent model;as a screening method,under the premise of ensuring approximate accuracy, it can reduce the number of experiments and provides samples as little as possible;as a design optimization method,it can obtain the optimal parameter combination that meets the objective.73

3. Progresses of design optimization application in plastic forming process

In view of complicated forming process, taking both accuracy and efficiency into account, the above numerical modelling methods, various optimization algorithms, knowledge reasoning technology,automatic control technology and AI technology are combined for wide design optimization application studies to reduce the gap between optimization results and actual production. The optimization for process parameters in forming process is still mostly based on the traditional DOP,which has been widely used to reduce costs and improve product quality and acquired good economic and social benefits. However, based on the influence of uncertain parameters on die wear, forming defects and product quality stability,UOP has been more and more widely used in recent years.Additionally, IDO based on knowledge and intelligent algorithms has got initial development currently. From aspects of DOP, UOP and IDO, this section will briefly introduce the progress of design optimization theories and technologies applied in forming process.

3.1. DOP application research

In order to reduce the number of function estimation, Gruber et al. proposed a method for dimension reduction modelling based on analytic and sequential quadratic programming(SQP)algorithm,which was applied to identify five parameters of flow stress,and then compared with the results obtained by traditional SQP algorithm.74Balagangadhar and Tortorelli effectively evaluated the forming response sensitivity by means of direct differentiation and combined this sensitivity with the nonlinear programming method to optimize the drawing and rolling process.75Brooghani et al. used the multi-level RSM to model the response of FE analysis, and realized the optimization of loading path in the process of tube hydroforming.76Ge et al. established the RSM based on least-squares support-vector machine (LS-SVM), and proposed a design optimization method for multi-object based on differential evolution to obtain the best fit of the internal pressure and the end feeding stroke.77In view of the defects such as wrinkle and springback in sheet forming process, Lee and Park performed the nonlinear static response optimization to structural parameters by means of equivalent static load method, and optimized the process parameters by means of RSM.78For reducing the energy consumption in the process of metal extrusion, Li et al. took the specific energy consumption of extrusion as the objective and established the equivalent equation of the thermal balance constraint.79Taking the initial temperature of aluminum bar, length of aluminum bar, extrusion speed,temperature of extrusion barrel,and die angle as control variables and regarding the thermal conductivity and the material strength coefficient as disturbance variables, they combined DOE with data analysis to establish robust optimization models of extrusion specific energy consumptions with thermal balance constraints. Fan et al. established the prediction models of fracture and dynamic recrystallization of the nickel-base superalloy Udimet 720Li under high temperature deformation.80Based on the optimization, the upsetting forming window of Udimet 720Li was obtained, which makes the blank have no damage and fracture, high recrystallization ratio and fine crystal structure. Considering the plastic strain,residual stress, damage evolution and material geometric parameter fluctuation in the process of riveting forming and strength test comprehensively, Roux and Bouchard carried out the global optimization of riveting quality based on KM,and thus improving the pull-out strength by 13.5% and the shear strength by 46.5%.81Xu et al. used topology optimization algorithm to reduce the weight of blank holder and manufacturing cost significantly in high strength steel stamping process.82

Xiao et al.and Zhang et al.both performed parameter optimization regarding the cross-section distortion of double-ridge rectangular tube in rotary draw bending, but the former was based on grey relational analysis and the latter was combined RSM with non-dominated sorting genetic algorithm II(NSGA-II).83,84Li et al. proposed a knowledge-based substep design optimization method. Combined virtual test design,RSM with GA, they carried out multi-objective DOP for the bending parameters of large-diameter thin-walled aluminum tube under the conditions of small bending radius and large bending radius.85Based on the Box-Behnken experimental design,Salehi et al.established the multi-level RSM of various quality characteristics. By means of artificial bee colony algorithm,they obtained the optimal combination of factors about the minimum drawing force, size error and maximum thickness distribution in the process of rectangular tube drawing.86Based on shared niches RBF GA and modified NSGA-II, Xie et al. optimized the blank holder force of sheet metal stamping.87Combining KM and GA, Abebe et al. performed the multi-objective optimization for stamping velocity, stamping force, and elastic pad thickness in the process of flexible multi-point forming of sheet metal, and obtained the Pareto front about dimpling and wrinkling.88By means of the technique for order preference by similarity to an ideal solution(TOPSIS),the optimal of Pareto front was obtained,and thus dimpling and wrinkling were eliminated effectively. To solve the problem of non-unique solution of the optimization for constitutive parameter characterization,a multi-objective optimization method considering flow curve and texture evolution in tension and compression was proposed to make the constitutive model conform to the physical reality.14

Based on FE simulation with anisotropic and isotropic constitutive models, Piglionico et al. used the central composite design method and multi-objective GA to determine the optimal process condition of 6061-T6 Al-alloy in the warm hydroforming process.89The results indicated the simulation by using anisotropic constitutive is significant for the design optimization robustness. Based on moving least squares (MLS)approximation, Oudjene et al.90and Ingarao and Di91established the RSMs and solved the design optimization problems in sheet metal forming process. The results showed that compared with the classical RSM method,this method can greatly reduce the calculation amount of design optimization in sheet metal forming process. In views of the high cost of conflict design optimization for multi-objective and the difficulty in determining the best compromise scheme in the Pareto front,Iorio et al. used Kalai-Smorodinsky method to transform the multi-objective problem into a single objective problem,which has been applied to the wire drawing process.92Based on proper orthogonal decomposition, Dang et al. established a reduced order model and developed an efficient KM that is combined with iterative optimization algorithm, which has been applied to springback control of U-shaped parts in the bending process.93By using incremental theory of plasticity,Zhang et al. established a quantitative relation model between the drawbead restraining force and forming quality to optimize the drawbead restraining force of stamping automobile panels effectively.94Wang et al. introduced time-dependent design variables in the optimization for sheet metal forming and to solve the subsequent problem of ‘‘curse of dimensionality”,they proposed a Gaussian process aided FA, and constructed an efficient simulation optimization based on the search mechanism perceived by agent model.95Wei et al. employed an unequal-thickness billet (UTB) with the initial volume distribution optimized by Box-Behnken design (BBD) and RSM,as illustrated in Fig. 8.96Therefore, the isothermal local loading forming (ILLF) of large-scale titanium alloy rib-web component can avoid folding defects and improve the filling ability of the transitional region.Wan et al.adopted a two-level optimization method: in the first-level, the structural layout and size parameters are taken as design variables, while in the second-level,the robust constraints and conventional aeroelastic constraints are considered to optimize the wing structures.97

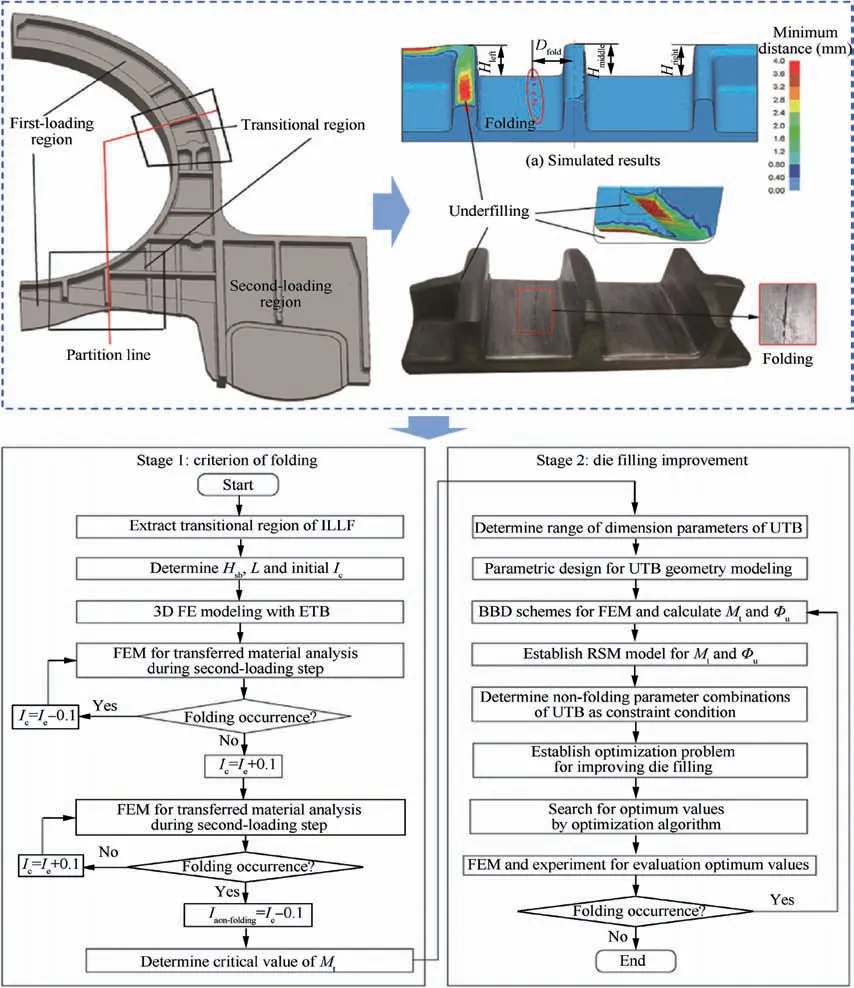
Fig. 8 Flowchart of UTB optimization procedure in transitional region of ILLF.96

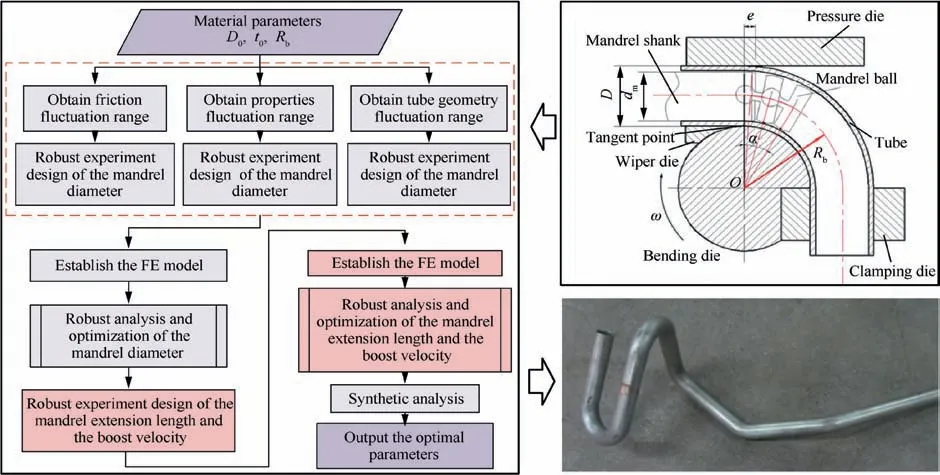
Fig. 9 Robust design optimization of larger diameter thin-walled Al-alloy tube bending.98,99

Dies and tools are important technical equipment in plastic forming process. The design optimization of dies for plastic forming plays an important role. Li et al.98–100investigated the neutral layer shifting and the role of mandrel in tube bending process,performed the robust design optimization of larger diameter thin-walled Al-alloy tube bending and realized the robust design of mandrel extension length and boosting ratio by considering the processing parameters such as the variations of friction, material properties and manufacture deviation of mandrel, as shown in Fig. 9. Xu et al.101proposed a significance-based optimization method for tube bending process, carried out the significance analysis of the processing parameters on the forming quality in terms of the maximum wall thinning ratio and the maximum cross section distortion degree, and obtained the optimum value of the significant parameter of bending mandrel and processing parameters.Darmawan et al.102conducted the deterministic design optimization for dies in cup drawing process and obtained reasonable blank holder force to ensure the springback of the dies ending within the allowable tolerance size.Behera et al.103used Taguchi methodology to optimize the laser equipment parameters such as laser power,scan speed,pulse diameter and pulse duration in Aluminum sheet laser bending, and confirmed the optimal results with a processing parameter of superior bending angle 20°.Alves et al.104combined with DOE and finite element simulation to investigate an innovative tubular end-toend joining by plastic instability,and they obtained the inclination angles 25° and 45° of the chamfered edges and two geometric ratios including the slenderness ratio lgap/r0between the gap opening and the reference radius of the tube, and the aspect ratio l0/libetween the initial unsupported height of the upper and lower tubes.

3.2. UOP application research

Introducing uncertain factors into the above deterministic analysis,scholars have carried out a large number of investigations on UOP. If the objective function, rather than the variance, is minimized, the optimization for reliability is used. If the focus of the optimization problem is to minimize the response variance, the optimization for robustness is applied.However, in many cases, both reliability and robustness can be considered simultaneously to maintain the robust optimal results.

As for the uncertainties of net-shape metal forming processes, by means of MC simulation, RSM and most probable point analysis, Ou et al. quantified the probabilistic properties of the shape and dimensional errors.21As shown in Fig. 10,they proposed a two-step optimization method to realize precise forming. Firstly, a direct compensation method for die shape modification is used to minimize the systematic errors.Then, the random fluctuation is reduced by a variable control method. Taking the forging of a two-dimensional aerofoil component and forward extrusion of a cylinder as cases, they verified the accuracy and robustness of the above optimization method. In view of the uncertainties in the U-shaped bending process of sheet metal,the blank holder force and the radius of punch-die were considered as design variables, the material properties, blank thickness and friction conditions were taken as design parameters, i.e. noise factors, and the mean value of the size deviation and the minimum standard deviation after the springback of sheet metal bending were taken as the optimization objective, Lafon et al. proposed a multi-objective RDO to tackle the effect of uncertainties.36,105Compared with KM, singular value decomposition of degree (SVDD) 2,SVDD 3 and NN, it is found that the mean square error of the meta model based on RBF was the smallest and the maximum of the R-square was 1. Additionally, the Pareto front was obtained based on NSGA-II with elitist strategy as shown in Fig. 11. Finally, a Pareto multi-objective decision-making method based on capability indices is proposed by considering the conflicting criteria of mean value and deviation. It is considered that the influence of uncertainty on the forming accuracy fluctuation can be effectively reduced by controlling the blank holder force.

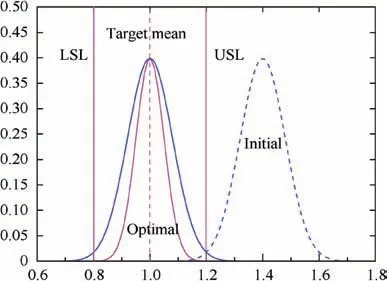
Fig. 10 Two-step stochastic optimization for net-shape forming operations.21

Fig. 11 Pareto front based on NSGA-II.36

Abdessalem and Abdelkhalak proposed an UOP method based on local agent model for T-tube hydroforming process.28This method only considered the possible instability defect region, and thus improving the efficiency of characterization and propagation computation of uncertain parameters in the forming process. Based on non-probabilistic interval model and KM, Huang et al. carried out the RBDO and RDO of loading path in the hydroforming process of T-shaped tube.24The interval model only needs to determine the boundary of the parameters, and does not need to consider its probability distribution. Zhu et al. proposed a six sigma robust design optimization method based on successive RSM to improve the reliability and robustness of the thermal protection system under uncertainty106. Gan et al. combined DOP with RDO,and proposed a robust design model based on uncertainty.The RDO and analysis of conformal expansion nozzle for unmanned aerial vehicle are carried out.107Li et al.performed the RDO for stamping process by means of Six Sigma.108On the basis of traditional RDO considering the uncertainties of parameters, the influence of the uncertainties of parameters and agent models on design optimization were considered synthetically. The results show that taking the error of agent model as an uncertainty factor and considering the influence of the uncertainties of parameters can effectively reduce the failure probability of cracking and wrinkling and improve the reliability of forming quality in production.

In view of the uncertainties in the tube hydroforming process, Huang et al. proposed a multi-objective RDO method of dual RSM considering both mean value and standard deviation.25The dual RSM was established based on RBF and sampling strategies by means of Latin hypercube and orthogonal experiment design. And then the robust Pareto front and the optimal case were obtained by using NSGA-II and ideal point method.Finally,the robustness of the forming process was improved significantly, but sacrificing the mean performance of the protrusion height. As for the uncertainties in the rolling process of sheet metal, Qiu et al. established a RSM by using SVM classification and support vector regression(SVR)and carried out high-dimensional RDO.109Taking tube rolling as a case,the result shows that the roundness error standard deviation by means of RDO is 62.2%less than DOP.In view of the forming stability of numerical control bending of tubes with multi-defects, taking the fluctuation of material mechanical parameters,the geometric dimension and size deviation of tubes, the instability of friction conditions and the manufacturing error of mandrel into account, Li et al. carried out the RDO for parameters of bending dies and process parameters successively by means of Taguchi method.98Based on dual-RSM for the mean and standard deviation of the die underfilling rate and NSGA-II of multi-objective optimization algorithm, considering the blank machining error, the stroke length and friction as noise factors, Wei et al. performed the RDO for the unequal thickness billet in the transition zone of titanium alloy isothermal local loading forming.110As for the problem that the defects such as wrinkling, fracture and springback are easily affected by the fluctuation of material properties and process parameters in the process of sheet metal forming, Kim et al. proposed a multi-attribute RDO method based on the Mahalanobis Taguchi system to improve the forming quality.111

In the crashworthiness design for vehicles,Sun et al.considered the influence of the uncertainties of double-hat structure stamping process on the phase from manufacturing to operation,and they used an agent model considering mean and standard deviation to simulate the forming and crashing responses,furthermore, a reliable solution was obtained by means of multi-objective PSO algorithm combined with MC simulation.Eventually, the optimization results showed that this method can improve the formability and crashworthiness significantly and enhance the reliability of the Pareto front.72As for crashworthiness optimization of vehicle thin-walled tubes considering sheet metal forming effects,Karago¨z and Yıldız compared recent metaheuristic algorithms including PSO, cuckoo search algorithm(CSO),gravitational search algorithm(GSA),hybrid gravitational search-nelder mead algorithm (HGSANM),league championship algorithm (LCA), FA, interior search algorithm (ISA) and imperialist competitive algorithm (ICA).The results showed that the HGSANM is the best.112

3.3. IDO application research

It is always the research focus for scholars to improve the efficiency of design optimization under the premise of ensuring its accuracy.IDO has become an innovative and efficient method for material constitutive behavior and process optimization in intelligent forming manufacture. In view of material constitutive behavior,by means of AI,many scholars adopted AI technology to develop new models. Li et al.113established a machine-learning based Johnson cook plastic model to capture the unconventional effects of strain rate and temperature on the hardening response of DP600 steel. This model is implemented into a material user subroutine and identified using a combination of analytical formulas along with a resilient back-propagation algorithm. It is found that the obtained machine learning based on the Johnson-Cook plasticity model can describe all experimental data with high accuracy, including both force–displacement and local surface strain measurements. Starting from the traditional regression mapping scheme, Zhang et al.114reconstructed the algorithm description of isotropic hardening von Mises plasticity, so that the relationship between strain and stress history can be modeled by NN function.The present work demonstrates that it is feasible to describe the stress–strain response of a von Mises material through a NN model without any explicit representation of the yield function,flow rule,hardening law or evolution constraints. Al-Haik et al.115proposed a stress relaxation prediction model for polymer matrix composites based on artificial neural network The predictions of the ANN model are found to be more accurate over a wider range of stress and temperature conditions than those of the explicit nonlinear viscoelastic model, in particular near the glass transition temperature. Usma et al.116combined an ANN model with a ratedependent crystal plastic finite element model (CPFEM) to predict the stress–strain behavior and texture evolution of AA6063-T6 under uniaxial tension and simple shear. The results presented in this research clearly demonstrate that the proposed ANN model provided significant computational time improvements without any major sacrifice in accuracy. Gorji and Mohr117present an ANN as an alternative approach to model the plasticity response in metal forming applications.A wealth of stress–strain curves for non-proportional loading paths is generated using a conventional plasticity model (virtual experiments). Subsequently, the architecture of a NN model is determined and the model trained based on the results from the virtual experiments.Jenab et al.118calculated the constants of Johnson-Cook, Khan-Huang-Liang and modified Voce by using GA and linear regression analysis (See Fig. 12), and used them to simulate the uniaxial tensile test.Two types of feed-forward back-propagation NN were also trained and validated to predict the rheological behavior of the alloy without the limitations of a mathematical function.

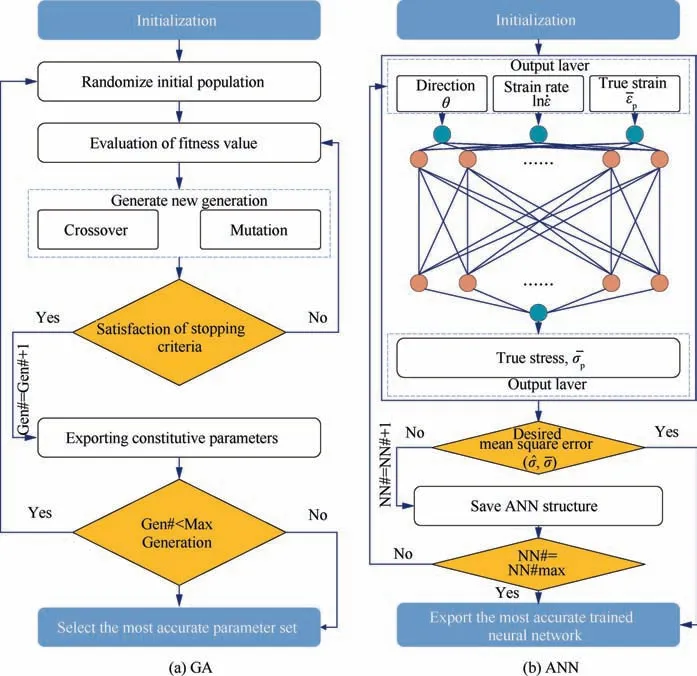
Fig. 12 Flowchart of GA and ANN structure used in constant calculation of Johnson-Cook, Khan-Huang-Liang and modified Voce models.118

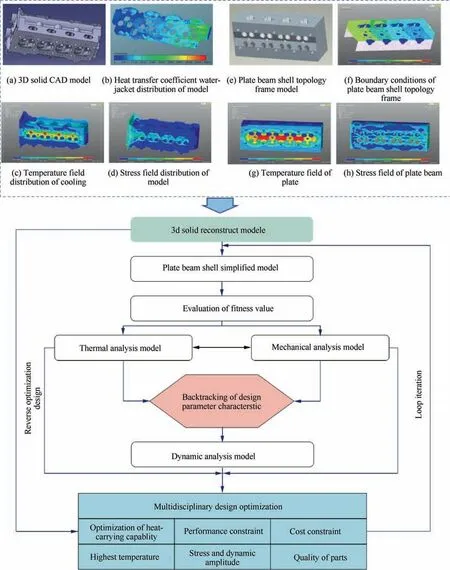
Fig. 13 Flow chart of design optimization of an engine cylinder head based on intelligent inference.

In view of forming process optimization, it is urgent to develop data-driven intelligent design process, viz., adaptive and automatic IDO for whole process chains by rule control,knowledge criteria and intelligent algorithms. With the aid of state function,forming quality function and learning updating law, Zhang et al. established an iterative learning control model (ILC) to optimize the structural dimensions of drawbead automatically, which is realized by integrating FE computer-aided engineering system into CATIA platform seamlessly and parameterizing the drawbead geometry.119Wang et al.120took the design optimization of the engine cylinder head as an example and proposed a design optimization method based on intelligent reasoning, as shown in Fig. 13.Through clustering analysis of continuous simulation data,the decision table is obtained,then the design parameter characteristics are backtracked by using data mining technology to guide the multidisciplinary design optimization of parts.Ducloux et al. established an automatic optimization engine for forging process,and realized the IDO of all the geometries in the forging process with multi-stages, i.e., Pre-forming,Blocker, Finisher.121By introducing GA into adaptive neuro fuzzy inference system (ANFIS), Yaghoobi et al. optimized the pressure loading paths in sheet hydroforming process and reduced the maximum thinning in the critical area of the part.122Kesvarakul et al. proposed a semi-forward adaptive simulation concept that can choose a practicable loading path for tube hydroforming process with a single FE simulation running.123Based on fuzzy logic control for the strain trajectory, the loading path can be ‘‘adapted” and adjusted to have the ability of keeping the forming strains within a preferred stain trajectory, so as to solve the highly non-linear forming behavior in tube hydroforming process efficiently. Naranje and Kumar proposed a knowledge-based system (KBS) for automatic strip-layout design of deep drawing sheet metal parts that was formed on progressive dies. This system is flexible, user-interactive and low implementation cost and can realize the IDO for forming dies.124By means of process sequence design, Park also proposed a KBS for nonaxisymmetric deep drawing parts with elliptical shape, which has four modules:shape recognition,three-dimensional modeling,blank design and process planning.This system can determine the drawing coefficient, the punch and die radii for elliptical shape parts.125Li et al. established an optimization rule for process parameters,viz.,the mathematical relationship between process parameters and forming defects.126In order to eliminate the forming defects, the above rule was adopted to calculate the iterative increment quantificationally, and a new IDO method for automobile panel forming was proposed,which has been applied to optimize the drawing ribs of deep drawing die for the body side and fender. Taking stamping of sheet metals and hydroforming of tubular metals as cases,Manabe discussed the application of intelligent adaptive inprocess control technology based on soft computing and sensing feedback system.127In view of the problems that shrinkage and flash are easy to occur and hard to control in the injection molding process,Yang et al.proposed a systematic method of on-line quality optimization for injection molding process based on digital image processing (DIP) and model-free optimization (MFO). This method has been embedded into the equipment of injection molding, and the DIP method is applied in detecting surface defects.128In view of the problem that huge computation amount and difficult implementation of design optimization are caused by many processes and passes in metal forming,Duda et al.proposed a multi-agent optimization framework to divide a single complex optimization problem into multiple tasks with relatively independent autonomous optimization,and the presented approach considered the working principles of a multi-agent model such as the messages flowing between agents and multi-criterion problem.129Based on a multi-agent model, Iannino et al. constructed a distributed intelligence-based system to model and self-optimize the production in smart factory.130Concentrating on thermal evolution and related material quality, as shown in Fig. 14, they established a virtual simulation platform for the design optimization of cyber-physical production systems.131The presented models were used to describe physical processes, computers, software and networks, and the approaches and algorithms for design optimization of whole process were performed and embedded into a new and comprehensive model-based software framework.

4. Trends and challenges of design optimization in plastic forming process

With the continuous expansion of forming connotation and extension, as well as the rapid development of computing science, data science and IoT, the theories and technologies of design optimization are also developing rapidly correspondingly to explore the potential of existing processes, develop new innovative processes, shorten the product development cycle and improve the product forming quality. Meanwhile,driven by the new round of technical revolution with intelligent manufacturing as the core and the demand of high-end equipment in aviation and aerospace, plastic forming will be developed towards high service performance, intelligent forming and green manufacturing. Therefore, new problems and challenges will be introduced into design optimization. In this section, considering the development trends of plastic forming,several key problems and challenges that may need to be faced and solved in design optimization for forming process are attempted to be discussed as follows.

(1) The connotation change of plastic forming is from focusing on the size and shape related dimensional accuracy to the integration of both shape forming and properties tailoring1,2,4,132–136Accordingly, the objective of design optimization tends from macro parameters to macro–micro coupling parameters, the dimensions of design optimization increase sharply, the response of objectives is highly nonlinear, the evolution parameters are rate-dependent, the response model is upgraded from macroscopic mean field to fully coupled thermal–mechanical-microstructure and multi-scale/cross-scale,and the design optimization process involves integrated computational materials, processing and service engineering. Due to the introducing of microstructure parameters and the objective of service performance,the difficulty in modeling and computation cost increases significantly.In summary,it is urgent to investigate the multi-scale design optimization because of the increasing requirements of precision forming with both shape forming and properties tailoring.

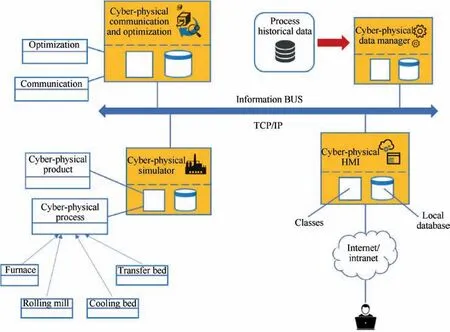
Fig. 14 Coherences between modules in virtual design of a cyber-physical production system.131

(2) Plastic forming extends from focusing on specific or single process to multi-operation and multi-pass with thermo-mechanical coupling.1,137,138This causes that the objectives of design optimization tends to integrated optimization of whole process and whole life cycle, viz.,manufacturing high-quality components not only depends on the optimization for single process, but also closely related to the manufacturing chains and service such as casting, rolling, heat treatment, joining, assembly and operating,which leads to large-scale global optimization,‘‘curse of dimensionality”and non-continuity,etc. Therefore, it is urgent to solve the industrial design optimization problem of the whole manufacturing process and life-cycle considering fabricating, forming and operating.

(3) Plastic forming should not only improve the forming potential of the selected materials, but also guarantee the high repeatability and stability of product quality.However, there are spatiotemporal uncertainties and their transitivity in the whole life-cycle of the products.For instance, a single forming process has uncertainty in material, geometry, loading, interaction and other aspects.29,137These uncertain parameters are difficult to control,which seriously affects the stability of manufacturing process. Therefore, UOP considering the above uncertainties need to be broken through.

(4) The balance problem between accuracy and efficiency of design optimization for plastic forming becomes prominent with the progress of plastic forming, which has been a bottleneck restricting the application of design optimization theories and technologies in practice. By using different design optimization methods with the combination of different sample selection, numerical modeling and optimization algorithm, different optimization results may be produced in terms of efficiency and accuracy. In response to the problems of multiobjective, high-dimensional, highly nonlinear and rate-dependent,based on a wide range of current design optimization methods and combined with supercomputing platform and multi-scale integrated computing methods,it is urgent to develop alternative models for reducedorder-modeling and massively parallel computing for highly efficient design optimization of forming process.

(5) Due to the development trend of plastic forming towards intelligent manufacturing, it is essential to develop design optimization methods with features of automation, networking and intelligence. Although some knowledge-based automatic design optimization methods and integrated computing platforms have been developed to integrate sample selection,numerical modeling and optimization algorithms,most of them are still based on manual operation and model-driven optimization. There are a lot of data, rules and various kinds of knowledge in production by forming, which is far from meeting the urgent requirements of online real-time design optimization in ‘‘Materials Genome Initiative”and ‘‘smart factory”. Thus, there is an urgent need to develop IDO for plastic forming from model-driven to data-driven based on emerging AI technologies such as big data, cloud computing and machine learning.1,48,139–144

5. Conclusions and remarks

In view of the key role of design optimization in the whole manufacturing cycle of plastic forming, scholars have carried out a lot of research on design optimization based on different algorithm combinations and different processes in different fields such as aerospace and automobile. In this paper, the design optimization framework in forming process was firstly summarized,the state of art of theories and technologies,such as DOP,UOP,numerical modeling methods and optimization algorithms,as well as application progress of design optimization in forming process are reviewed. The applicability of various modeling methods and optimization algorithms in solving the design optimization problems in specific forming process is briefly illustrated. Considering the development trends of forming technology, several challenges in design optimization of forming that need to be solved are attempted to be discussed. The main conclusions and remarks are as follows:

(1) Compared with DOP, the concept and method of UOP have been paid more and more attention in recent years.RBDO, RDO, WCSBO and NPM have been developed by introducing probability and statistics theory, fuzzy theory and interval analysis.RBDO and RDO are often considered together to meet the actual requirements of the process. However, the analysis of Pareto front with multiple objectives and conflicting objectives remains to be solved.

(2) At present,the main design optimization methods are all model-driven. In view of the cost and efficiency of FE method, MC method, Taguchi method, sensitivity analysis,meta model and other numerical methods are developed to combine with reliability method for design optimization calculation. Meta model method has been greatly developed for its high efficiency and simplicity,mainly including RSM, KM, SVM, RBF and NN, etc.

(3) There are many kinds of optimization algorithms.According to whether to solve the derivative of different orders of the objective function, the optimization algorithms are usually divided into iterative algorithm and heuristic algorithm. Heuristic algorithm can solve complex problems such as large space, nonlinear, global optimization, combination optimization, etc. This algorithm mainly includes evolutionary algorithms, artificial NN algorithms and swarm intelligence algorithms.These methods are complementary to each other,which have attracted more and more attention and been applied in the field of design optimization in forming process in recent years.

(4) Challenges that need to be addressed may include: the multi-scale design optimization required by precision forming with both shape forming and properties tailoring; the industrial design optimization problem of the whole manufacturing process and life-cycle considering multi-pass fabricating, forming and operating; UOP considering the uncertainties in material, geometry,loading, interaction and other aspects; design optimization with matching of precision and efficiency by developing reduced order method;data-driven IDO of plastic forming.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors would like to thank the National Natural Science Foundation of China (Nos. 51775441 & 51835011), the National Science Fund for Excellent Young Scholars (No.51522509) and Research Fund of the State Key Laboratory of Solidification Processing (NWPU) of China (KP201608).