Analytical method of nonlinear coupled constitutive relations for rarefied non-equilibrium flows
Zhiqing HE, Zhongzheng JIANG, Hungwei ZHANG, Weifng CHEN,*
a School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, China
b Department of Mechanical Engineering, National University of Singapore, Singapore 117576, Singapore
KEYWORDS Knudsen number;Microscale flow;Non-equilibrium;Nonlinear constitutive relations;Rarefied gas
Abstract It is well known that Navier-Stokes equations are not valid for those high-Knudsen and high-Mach flows, in which the local thermodynamically non-equilibrium effects are dominant. To extend the non-equilibrium describing the ability of macroscopic equations, Nonlinear Coupled Constitutive Relation (NCCR) model was developed from Eu’s generalized hydrodynamic equations to substitute linear Newton’s law of viscosity and Fourier’s law of heat conduction in conservation laws. In the NCCR model, how to solve the decomposed constitutive equations with reasonable computational cost is a key ingredient of this scheme.In this paper,an analytic method is proposed firstly.Compared to the iterative procedure in the conventional NCCR model,the analytic method not only obtains exact roots of the decomposed constitutive polynomials,but also preserves the nonlinear constitutive relations in the original framework of NCCR methods.Numerical tests to assess the efficiency and accuracy of the proposed method are conducted for argon shock structures, Couette flows, two-dimensional hypersonic flows over a cylinder and threedimensional supersonic flows over a three-dimensional sphere. These superior advantages of the current method are expected to render itself a powerful tool for simulating the hypersonic rarefied flows and microscale flows of high Knudsen number for engineering applications.
1. Introduction
A deep reform has been taking place in the field of fluid mechanics in the past half century, during which the scope of fluid mechanics is extended from macro to micro and also from the ground to the space. As the altitude increases, the air density decreases gradually and the mean free path of the air molecules can be comparable to the relevant characteristic length scale of the studied problems. The Knudsen number(Kn), defined as the ratio of molecule mean free path to characteristic length, can be used to divide four different flow regimes, i.e. continuum regime, slip regime, transition regime and free molecular flow regime, corresponding to Kn ≤0.01,0.01
Boltzmann equation is the core of study in the rarefied nonequilibrium flow. It describes the statistical behaviour of a thermodynamic system deviating from equilibrium state and thus can describe all of the four flow regimes mentioned above. However, there are many challenges in solving the Boltzmann equation because of its complex collision term.To accurately simulate the non-equilibrium dynamics, many effective theories and numerical methods are proposed based on Boltzmann equation. One of them is stochastic particle methods, such as Direct Simulation Monte Carlo (DSMC)7,8method which has always been used as a standard for validating other methods in numerical simulations. DSMC is recognized as the most reliable method for flows of high Knudsen number. However, DSMC faces stochastic fluctuation in low-speed flows and prohibitively high computational costs in the near-continuum regime due to the limitation of time steps and cell sizes. The others include deterministic method,such as Discrete Velocity Method (DVM),9,10Fast Spectral Method (FSM),11Unified Gas-Kinetic Scheme (UGKS),12–14Discrete Unified Gas Kinetic Scheme (DUGKS)15,16and Gas-Kinetic Unified Algorithm (GKUA).17–19There is no stochastic fluctuation issue in these methods, but heavy computational cost caused by velocity space discretization inhibits its wide engineering application, especially for hypersonic flows.
Chapman-Enskog expansion method20–22and moment method23–27extend the scope of N-S equations from the continuum regime to those flows which are not far from the equilibrium. Burnett equations and Grad-type equations are the most representative ones of them.25,28,29However, Grad’s 13-moment equations encounter non-physical sub-shock problems beyond a critical Mach number30,31and conventional Burnett equations are contradictory to Gibbs relation32,33in some terms. They also violate the second law of thermodynamics, and encounter computational instability under some unfavorable conditions. These unsatisfactory properties limit their prediction ability in high-speed and low-density flow regimes. Some measures were also taken to remedy these methodologies, for example, the Simplified Conventional Burnett (SCB) for multidimensional hypersonic flow,22the regularized 13-moment equations23(R13) and regularized 26 moment equations34(R26). However, many problems still exist, e.g. complex additional higher boundary conditions.
To minimize the deficiency of the N-S equations in the rarefied regime and overcome the instability and efficiency problems of other methods, Eu proposed Generalized Hydrodynamic Equations (GHEs).35–38In Eu’s theory, the kinetic theory is strictly connected to extended irreversible thermodynamics. Through constructing a non-equilibrium canonical distribution function to connect entropy production with dissipative evolution of macroscopic non-conserved variables, the GHE is strictly enforced to be consistent with the second law of thermodynamics, which includes a set of evolution equations based on the distribution function within the framework of 13 moments.GHE has been successfully applied to calculate the shock structure profile for high Mach numbers and it gave results in good agreement with experiments.39A linearized version of GHE was also used to study sound wave absorption and dispersion in molecular gases,40which yielded good agreement with experimental data in nitrogen,hydrogen,deuterium,and HD(hydrogen-deuterium).However,it is very difficult to extend GHE to multi-dimensional problems because of the existence of the highly nonlinear coupled complicated terms for non-conserved variables, which limits its application in modern computational fluid dynamics.
To solve multidimensional problems efficiently, Eu and Myong simplified GHE to a nonlinear algebraic system using adiabatic assumption39and balance closure,41which is called as Nonlinear Coupled Constitute Relations (NCCRs). By decoupling NCCR into two directions, i.e. the compression expansion direction and the shear direction, the decomposed algebraic system can be solved by the iterative method.42One-dimensional shock wave structure and two-dimensional flat plate flow problems for monatomic gases have been used to validate the capability of the NCCR model in capturing the flow physics of high-speed and low-density flow regions.43
Subsequently, the NCCR model was extended to a diatomic gas by considering excess normal stress associated with the bulk viscosity of gas and was adopted successfully in the two-dimensional hypersonic rarefied flow around a blunt body.44More investigations45–51have been performed,including a discontinuous Galerkin method on unstructured grid developed for NCCR model,49–51an undecomposed NCCR solver developed by Jiang et al. in three-dimensional implicit Finite-Volume Method (FVM) framework52–56and a new enhanced wall boundary condition based on NCCR model for micro-Couette flow.57Even though NCCR model is considerably simplified compared to original GHE, it is still difficult to be implemented and solved. One has to use iterative method to solve NCCR because of its high nonlinearity,which leads to the twice to three times higher computational cost compared to that of N-S equations.
In the present work, to overcome the foregoing complexity and inefficiency of the NCCR iterative solver, we aim to develop a simplified analytical method for the NCCR model.It is realized by expanding the nonlinear factor of the NCCR model around the equilibrium state and retaining the relevant terms until the second order of accuracy. After the simplification, the traditional nonlinear coupled constitutive relations can be solved by analytical method instead of the iterative one.Therefore,the new method is more efficient and also preserves the capability of describing non-equilibrium flows. The rest of the paper is structured as below. Nonlinear coupled constitutive relations and conventional iterative method are introduced in Section 2. The expansion and truncation of the nonlinear factor are then presented in Section 3 to obtain the analytical method and comparison with the iterative method.In Section 4, benchmark test cases are conducted to assess the accuracy and efficiency of the proposed model, which are followed by the conclusions in Section 5.
2. Governing equation
2.1. Generalized hydrodynamic equations and nonlinear coupled constitutive relations
The governing equations of conserved variables(i.e.ρ,ρu and ρE in Eq. (1)) and non-conserved variables (i.e. ∏and Q in Eqs. (2) and (3)) for monatomic gases, i.e. Eu’s generalized hydrodynamic equations36, read

where κ can be specified as a Rayleigh dissipation function36

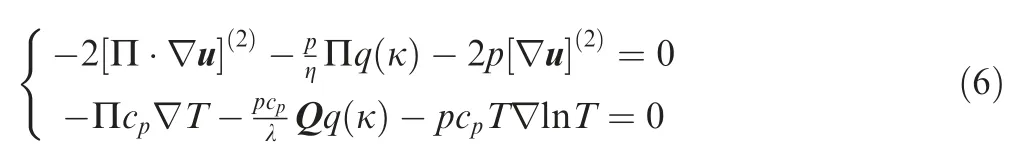
The following dimensionless variables and parameters are introduced:
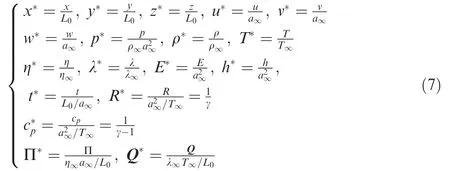
where L0is the reference length,a is the speed of sound,h is the total enthalpy per unit mass,R is the specific gas constant,and γ is the specific heat ratio.Here quantities with subscripts‘‘∞”represent the inflow parameters, whilst the superscript of the asterisks denotes the dimensionless parameters, which will be omitted below for brevity.
With Eq. (7), the dimensionless governing equations of the conserved variables, i.e. Eq. (1), for monatomic gas read
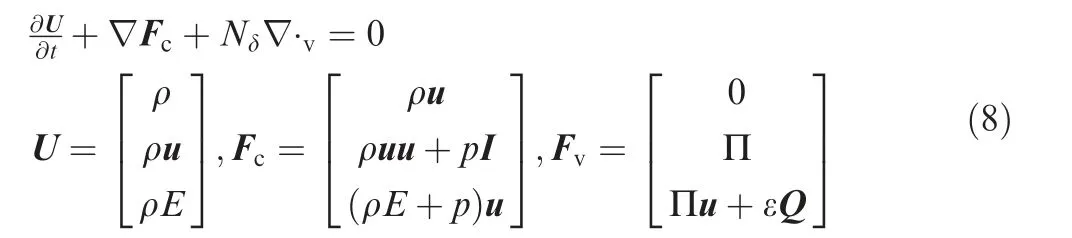
where U is the solution vector of conserved variables,Fcis the inviscid flux vector,and Fvis the flux vector related to the nonconserved variables. Nδand ε are given by

2.2. Decomposed algebraic system for NCCR model
The dimensionless NCCR model, i.e. Eq.(11), is a set of algebraic equations with high nonlinearity and is difficult to be solved, even though it has been greatly simplified from GHE.36A decomposed nonlinear algebraic system of the NCCR model was proposed by Myong,42which can be solved by an iterative method. The iterative process of the NCCR model does not need to solve a coupled hyperbolic system with higher-order variables such as Grad’s 13-moment equations,25but only requires an additional procedure to calculate the stress and heat flux from the decomposed nonlinear algebraic system separately and then implement them in the equations of the conversed variables, i.e. Eq. (8), which shares a similar feature with the traditional N-S equation to solve the five components of conserved moments. Although Jiang et al. developed an undecomposed hybrid algorithm for NCCR,54its intrinsic complexity renders it difficult to be implemented.Also, its convergence characteristic has not been tested and therefore is still not clear. Nevertheless, Myong’s decomposed solver can be mathematically proved to be converged and seems easy for implementation. Therefore, the decomposed solver by Myong42will be adopted in the current work.
Variables with the subscript 0 correspond to stress from linear Newtonian law and the heat conduction from linear Fourier’s law.
2.2.2. Shear flow solver
The decomposed solver in the two shear directions j and k of xiplane is
2.2.3. Recombination of two decomposed solvers


Table 1 Description of unified notation and rotation index.
Then substitute these variables back into the conserved variable equation, i.e. Eq. (8), to continue the time marching.
3. Analytical NCCR model
Although the NCCR model has been simplified and decomposed compared to the Eu’s original equations,42its numerical solution is still not straightforward to be obtained due to its high nonlinearity. Conventional iterative algorithms include the fixed-point iterative method, Newton’s method, and coupled method.54However, all these methods need numerous iteration steps to obtain the converged solutions from the initial conditions and may diverge under some unfavorable conditions.
To overcome the deficiency of the iterative method,we will develop an analytical method for the NCCR model in this work. Since c is a positive value close to 1 and ^R can be used to measure the degree of nonequilibrium,47we start with the Taylor expansion at c^R=0 for the nonlinear factor q c^R in Eqs. (2) and (3), i.e.,

For flows in near space or in micro-electro-mechanical systems where the rarefaction and non-equilibrium effects are not as strong as those in highly transitional flows and free molecular flows,1the higher-order terms at the left-hand side of Eq.(21) can be truncated, and only the first- and second-order terms are retained, i.e.

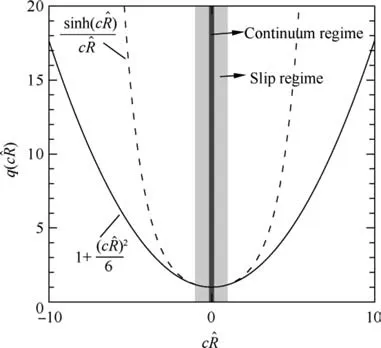
Fig. 1 Function curves of nonlinear factor q c^R and its truncated version.

3.1. Compression and expansion solver

3.2. Shear flow solver

However, there is no algebraic expression for the solutions of general quintic equations over the rationals.As a result,Eq.(25) cannot be solved analytically. Alternatively, an approximation method is introduced to obtain the solutions instead of conventional iterative methods. Specifically, combining Eqs. (16) and (17) yields


Fig. 2 Comparison between x5-2x4 and -2.904433x4 on the interval -1,0[ ].
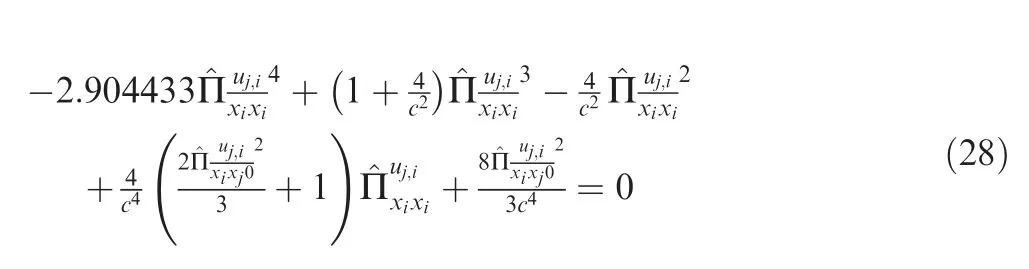
Similarly,it is shown that there is a unique real root for Eq.(28)if-1 ≤≤0.Exact root can be derived from Eq.(28)and the interested readers can see Appendix B for the detailed information.
3.3. Comparison with Myong’s decomposed solver
In Sections 3.1 and 3.2, a new analytical method for decomposed NCCR system is proposed. Compared to the conventional iterative methods used for Myong’s decomposed solver,42the analytical method is expected to be more efficient since the exact roots of the decomposed constitutive polynomials can be directly achieved. Meanwhile, it also preserves the nonlinear constitutive relations in the framework of the NCCR method.
To illustrate the different nonlinear properties of the analytical and iterative methods, the constitutive relations for compression and expansion as well as shear flow problems(c=1.0179) are respectively shown in Figs. 3 and 4. The NS stresses from the linear constitutive relation are also added for comparison. In general, the solutions from the analytical method are close to those from Myong’s decomposed solver for both normal and shear directions. They share the same mathematical properties as those of the solutions achieved through the iterative method for NCCR model by Myong42,i.e.
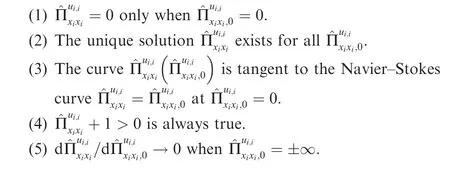

Fig. 3 Comparison of solutions from analytical and iterative method of NCCR model with N-S linear constitutive relation for compression and expansion problem (c=1.0179).
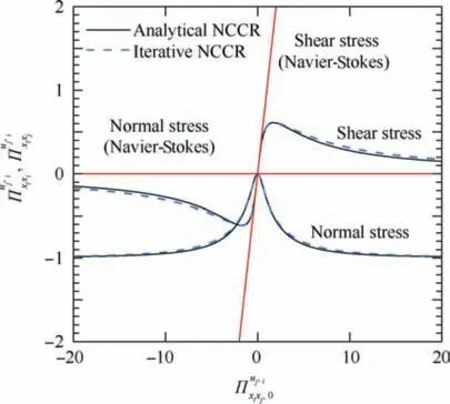
Fig. 4 Comparison of solutions from analytical and iterative methods with the N-S linear constitutive relation for shear flow problem (c=1.0179).

Fig. 5 compares the number of iteration steps under different initial conditions for the iterative and analytical methods.Note that for the latter only one step is needed as shown in Fig. 5. For the iterative NCCR model, it generally takes at least 6–13 iterations for compression and expansion solver whilst takes 2 iterations for shear flow solver. Generally, the analytical method reduces total computational time considerably due to its non-iterative calculation.

Fig. 5 Computational cost of analytical and iterative NCCR methods.
3.4. Summary of analytical NCCR model
The entire essence of the analytical NCCR method is described in a detailed flowchart as shown in Fig.6.Briefly summarizing,Eu developed the generalized hydrodynamic equations from Boltzmann equation based on a nonequilibrium canonical distribution function and a cumulant expansion of the collisional integral,36and next,with adiabatic assumption36and balanced closure,41NCCR model was developed.A decomposed nonlinear algebraic system of the NCCR model was then proposed by Myong, and by performing iterative method, the nonlinear algebraic system can be solved.42In this paper, by expanding the NCCR nonlinear factor around the equilibrium state and retaining the relevant terms until the second order of accuracy,we can solve the NCCR model with analytical method.Finally, we have the analytical NCCR method.
4. Results and discussion
In this section, several typical nonequilibrium flows, including shock wave structure (1D), Couette flow (quasi-1D), hypersonic flow past a cylinder (2D) and supersonic flow past a sphere (3D), are selected to validate the computational accuracy and stability of the proposed analytical NCCR method.
4.1. Shock wave structure of argon
The one-dimensional steady shock wave structure of argon gas is a benchmark case for validation of non-equilibrium models.58The initial conditions in the upstream and downstream of shock wave can be determined by the Rankine–Hugoniot relations,58i.e. (Note that the subscripts ‘‘0” and ‘‘1” indicate the states before and after the shock, respectively)
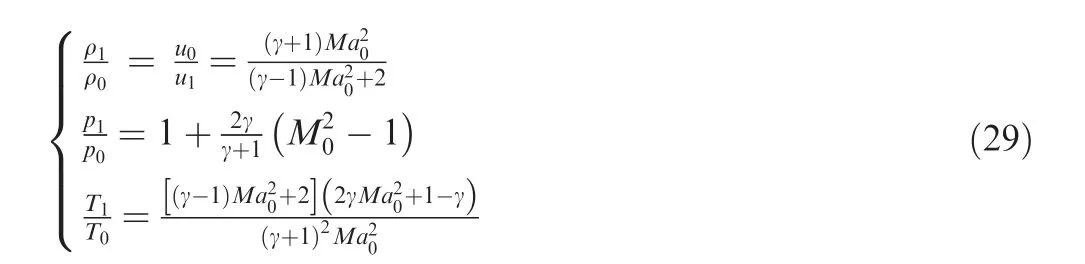
The dynamic viscosity of argon is estimated using the inverse power law,54i.e.

where Tref, ηrefand s are reference temperature, reference dynamic viscosity and temperature exponent, respectively.The properties of argon used in the computations are given in Table 2.58
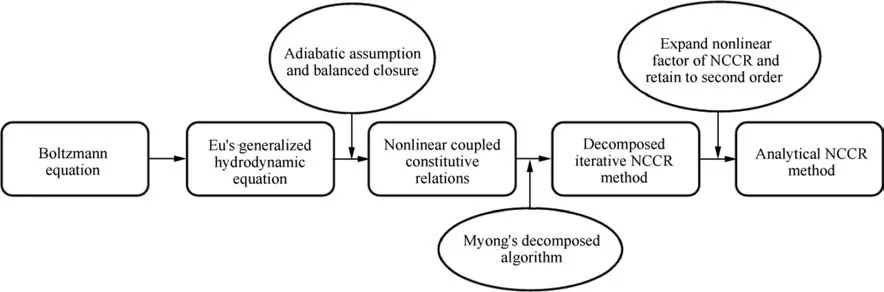
Fig. 6 Flowchart showing derivation process of analytical NCCR method.
In order to evaluate the performance of the analytical NCCR model, a series of test cases are investigated, which are characterized by different Mach numbers, ranging from Ma=1.2 (the N-S equations are still valid) to 9.0 (the strong non-equilibrium effects are dominant).
Simulations based on Myong’s iterative method and the developed analytical method are firstly conducted for the hard-sphere molecules at Ma=1.2,2.0 and 3.0.Ohwada’s full Boltzmann equation solutions61and N-S solutions are also added for comparison. The exponent s in Eq. (30) is assumed as 0.5 and the constant c in NCCR model is 1.190858. Fig. 7 shows the non-dimensional density, temperature, stress, and heat flux inside a shock layer for Ma=1.2, 2.0 and 3.0. They respectively take the following forms:

where the quantities with subscript‘‘0”represent the upstream parameters of the shock wave. The horizontal axis is normalized by mean free path l0. In Fig. 7(a), with Ma=1.2, both NCCR and Boltzmann solutions are almost the same as N-S results since the flow is not far from equilibrium.As the Mach number increases to 2.0 and 3.0, the NCCR model performs better than the N-S equations when both solutions are compared to the Boltzmann counterparts,especially in shock rising position.Moreover,the results of the analytical NCCR model are close to those from the NCCR iterative method, which indicates that the approximation of the analytical algorithm is reasonable in the calculation of one-dimensional shock wave structure and it has nearly the same performance with the iterative model under the studied Mach number conditions.
The shock wave structure of argon at higher Mach numbers, i.e. Ma=8.0 and 9.0, are investigated based on the two NCCR models. The exponent s in Eq. (30) is assumed as 0.72 and the constant c in the NCCR model is 1.0179.58The solutions of the non-dimensional density, temperature,stress and heat flux inside a shock layer are shown in Fig. 8,and the solutions evaluated by Bird’s 1D DSMC code62and experimental measurements63,64are also presented for reference.The scaled density and temperature are obtained through

where the quantities with subscript ‘‘1” represent the downstream parameters of the shock wave. Stress and heat flux are normalized with Eq. (31). The maximum gradient-length local Knudsen number, which is proposed by Boyd et al. as a continuum breakdown parameter,65,66is introduced to describe the degree of non-equilibrium state, i.e.

where l is the mean free-path and Q is a variable of interest,such as density, temperature or pressure. Higher value of KnGLLrepresents higher degree of non-equilibrium. Based on Fig. 8, KnGLLreaches its peak value at upstream region of shock wave (i.e. x/l0≈-3), where the strong nonequilibrium effect exists.In the upstream region of shock wave,the results from our analytical method are closer to the DSMC and experimental results than the iterative method results,whose shock profiles rise later. In addition, the underestimation of both stress and heat flux in the iteration NCCR method is observed in the upstream region and the analytical method alleviates it to some degree. This may be due to the fact that the original nonlinear factor q c^R of NCCR model is not quite physical in very strong non-equilibrium regimes.59In the downstream region of the shock wave where the nonequilibrium effect is relatively weak (i.e. smaller KnGLL), the results from the iterative and analytical methods are similar.As we noted earlier, DSMC has been used as a standard,and Fig.8 shows that DSMC results agree with the experimental data very well. Moreover, there are limited experiments in low-density monatomic gas flows. Hence, DSMC simulations will serve as benchmarks for the following cases.
4.2. Couette flow
Here the Couette flow problem67is selected to examine the capability of the analytical NCCR method for low-speed flows.The Couette flow is driven by two infinite flat plates moving parallel to opposite directions with constant speed u0.The temperature of each wall is Twand the distance between the two flat plates is L. The global Knudsen number is used to represent the degree of non-equilibrium effect67, i.e.

Here u0=50 m/s and Tw=273 K are adopted, while L is varied based on different Knudsen numbers.
Enhanced NCCR-based slip boundary conditions proposed by Jiang et al.57are adopted for the walls, which read

Here Rfis the relaxation factor and is set to be 2.0×10-6suggested by Jiang et al.57Argon is used to simulate the Couette flow.The exponent s in Eq.(30)is assumed as 0.75 and the constant c in the NCCR model is 1.0179.42
Fig. 9 shows the velocity distribution of Couette flow predicted by different methods for Kn=0.012, 0.10, 0.25, 0.50,0.75 and 1.00. They represent different non-equilibrium situations from continuum regime to transition regime.The DSMC and R13 results by Refs.24,68 are also demonstrated for comparison. At Kn=0.012 and 0.1, Fig. 9(a) and (b) show that the velocity profiles predicted with R13, analytical NCCR method and N-S equations are in excellent agreement with the DSMC results.As the Knudsen number increases,the predicted velocity profiles of the foregoing methods show pronounced difference from those from the DSMC approach,which indicate an underlying non-equilibrium phenomenon in the micro-Couette flow. Weakly nonlinear velocity profiles can be observed in Fig. 9(d)–(f), where all the models fail to capture except DSMC. However, the velocity profiles predicted by analytical NCCR method and the R13 model are closer to DSMC results than those by N-S equations.The profiles obtained by the analytical NCCR are very close to those by the R13 model,even though R13 model is the evolution equations of 13 moments and the analytical NCCR method is much simpler evolution equations of 5 moments.
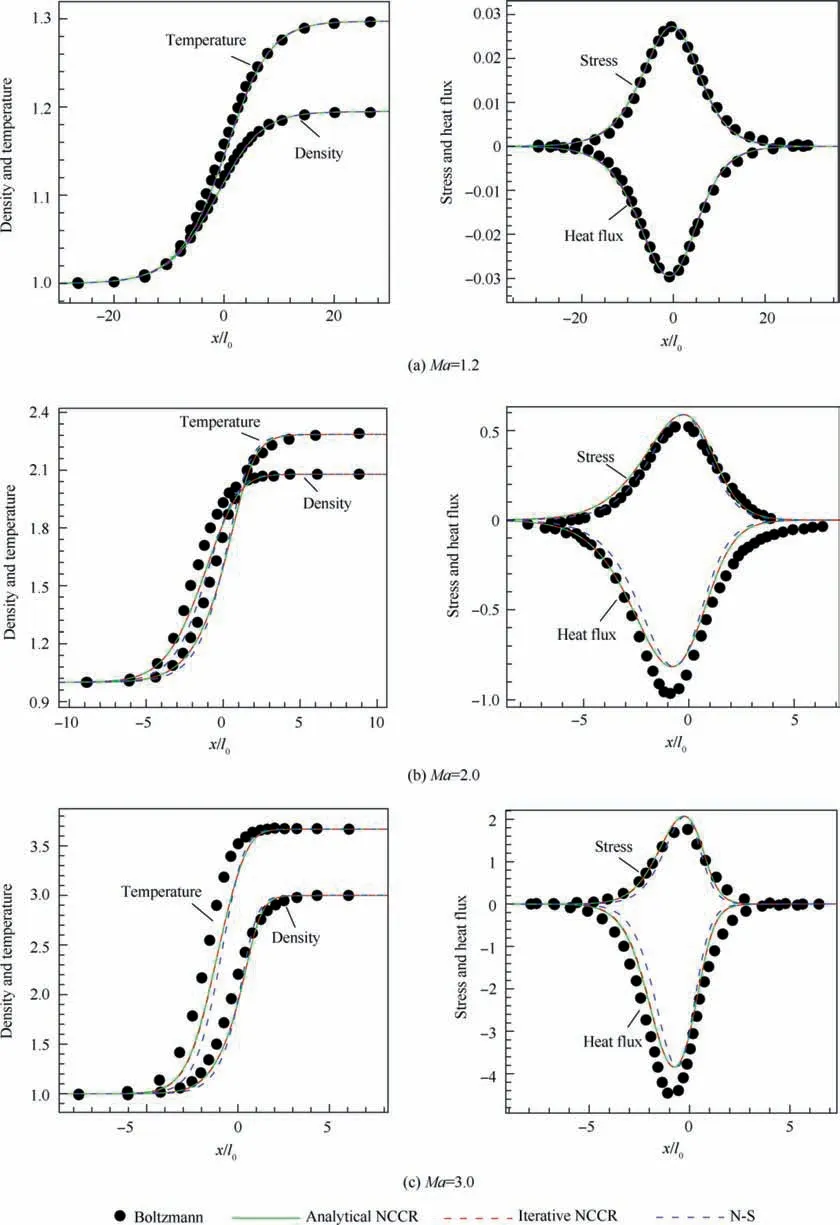
Fig. 7 Comparison of analytical and iterative NCCR models for argon shock waves.
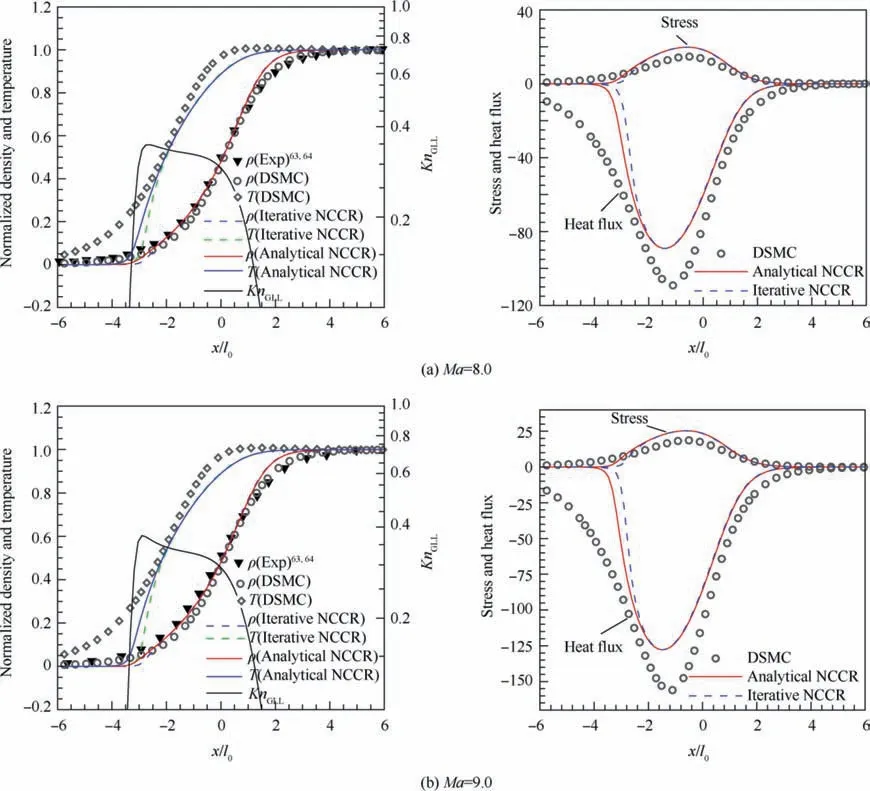
Fig.8 Comparison of analytical and iterative NCCR models for argon shock wave(DSMC results are evaluated with Bird’s 1D DSMC code62).
The temperature distribution of Couette flow predicted by different methods is shown in Fig. 10. As can be seen from Fig. 10(d)–(f), the linear N-S equations with first-order Maxwell slip boundary conditions do not capture the nonequilibrium effects at walls for Knudsen number above 0.5.The R13 and NCCR profiles are closer to the DSMC results than the linear N-S results, although their results start to diverge from the DSMC profiles at Kn=0.25, where the R13 overestimates and the NCCR model underestimates the temperature in the central region of the Couette flow. For Kn ≥0.5,the temperature decrease predicted by the analytical NCCR method is much closer than those of the R13 and N-S.However, the limitation of the analytical NCCR method is also shown in the central regions for Knudsen number above 0.1, because it gives lower temperature at these regions. The behavior of the analytical NCCR method is more like the linear NS equations in these regions, but it performs better at walls and gives better temperature jump values than the R13 and the N-S equations when compared to the DSMC results.
Since a better performance of the analytical NCCR method is shown in the above results, its capability still deserves to be investigated more carefully. The normal heat flux and shear stress distribution of Couette flow predicted by different methods over a range of Knudsen numbers from 0.1 to 1.0 are shown in Fig. 11. Because of the symmetry of the flow field in Couette flow, only the upper-half distribution of the heat flux and shear stress profiles is plotted. At Kn=0.1, normal heat flux and shear stress from all the methods agree well with the DSMC results.However,with increased Knudsen number,the degree of nonequilibrium increases. Difference arises among the results from different methods. In the transition regime, Fig. 11 presents constant shear stresses across the domain for the planar Couette flow. The deviation between the three continuum-based hydrodynamic models and the DSMC method increases as the flow deviates from the thermal equilibrium with about 7% overestimation at Kn=0.25, 0.5 and 9% overestimation at Kn=1.0. For normal heat flux,the results predicted by the linear N-S equations deviate from the DSMC results for Kn>0.1. However, both the R13 and analytical NCCR methods show fairly good agreement with the DSMC results for Kn<1.0, except for the nonlinear behavior near the wall. For Kn=1.0, all the three continuum-based hydrodynamic models deviate from the DSMC results,but the R13 and the analytical NCCR methods perform much better than the N-S equations.
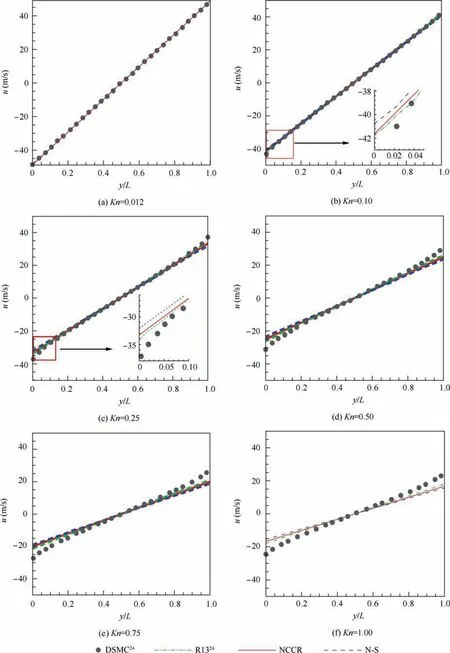
Fig. 9 Velocity distribution of Couette flows predicted by different methods over a range of Knudsen numbers.
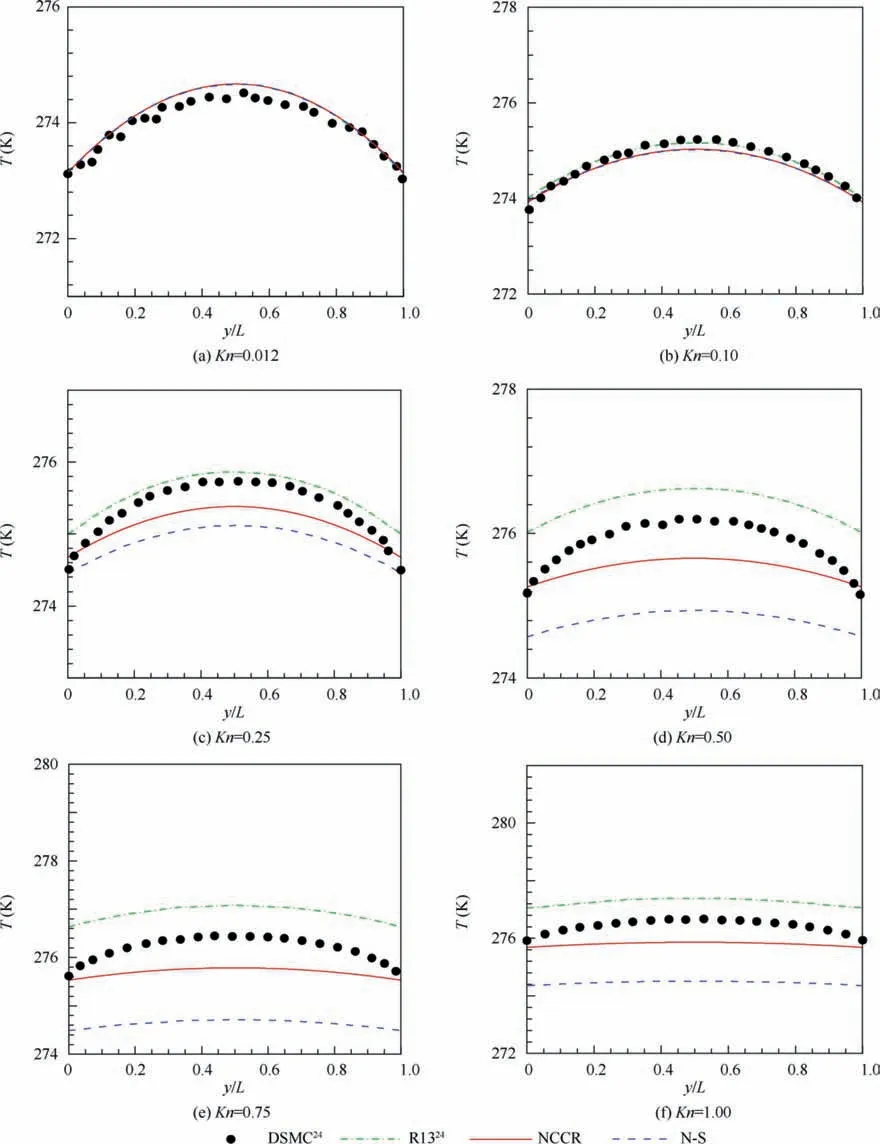
Fig. 10 Temperature distribution of Couette flow predicted by different methods over a range of Knudsen numbers.
4.3. A hypersonic flow around a 2D cylinder for argon gas
The analytical method is further validated for argon gas flows around a 2D cylinder with radius of 0.1524 m where Ma=10 and Kn=0.004,0.02,0.1(The characteristic length is the radius of the cylinder). The free-stream conditions are taken from Ref.66, where corresponding densities of the free-stream gas are 1.408×10-4, 2.818×10-5and 5.636×10-6. The first-order Maxwell slip boundary condition is applied at the wall surface and other calculation parameters are shown in Table 3.

Fig.11 Normal heat flux and shear stress distribution of Couette flow predicted by different methods over a range of Knudsen numbers.
Since the prediction of the temperature profile is more difficult than those of density, velocity, and pressure, only the temperature on the stagnation line is presented in Refs. 59,66 Therefore,only the temperature predicted from different methods are shown in Fig.12.Gradient-length local Knudsen number (KnGLL) of each case is also plotted for comparison.Continuum hypothesis is not valid if KnGLLis greater than 0.05.66Therefore,the non-equilibrium effect needs to be taken into account inside the shock at each case.
At Kn=0.004, which corresponds to the continuum flow regime, the temperature profiles predicted by N-S and NCCR are close to the DSMC solution. Nevertheless, at Kn=0.02,which belongs to the slip flow regime,the results from different constitutive relations start to deviate from that of the DSMC,especially at regions inside shock wave where KnGLLis higher.Both of the two NCCR methods yield better results than the N-S constitutive relations, and they provide almost the same results. Moreover, at Kn=0.1, which is in the transitional flow regime, both methods are better than N-S equations. It should be highlighted that the analytical method provides even better results than iterative one although it is an approximation of NCCR for the situation which is not far from the equilibrium.It indicates that the analytical method is a reliable and efficient way to solve those far-from-equilibrium flows.
The computational efficiency of analytical method and iterative method is investigated based on the same computer infrastructure. The average computation time per step of cases above for 10,000 steps at 11,440 structured grids is listed in Table 4. About 1/3 of the computation time on average is saved for these cases in the calculation of the inviscid flux and other computational overhead. It can be expected that more pronounced speed-up can be achieved when complex geometries discretized with millions of grids are considered.

Table 2 Physical properties of argon58.

Table 3 Calculation parameters for hypersonic flow past a cylinder.
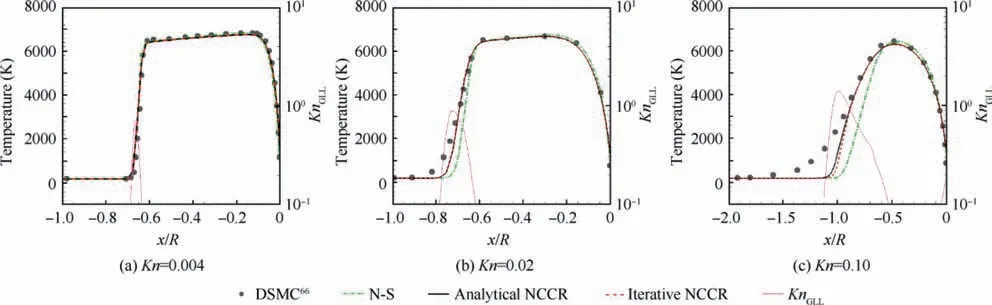
Fig. 12 Temperature and maximum gradient-length local Knudsen number KnGLL along the stagnation line of Ma=10 cylinder at different Kn.
4.4. A supersonic flow around a 3D sphere for argon gas
The analytical NCCR method is validated for monatomic gas flows around a 3D sphere with a radius of 1.9 mm in slip regime. Compared to the two-dimensional case in Section 4.3,here we would like to examine the ability of the analytical NCCR method in predicting 3D problems. The monatomic gas is assumed argon with s=0.75 in the inverse power law and c=1.0179. The inflow parameters are given in Table 5.
To reduce the computational cost,a quarter of the computational domain is considered in this work. Typical structured grids of the computational domain are demonstrated in Fig.13 with 80 nodes in the radial direction of the sphere. First-order Maxwell slip boundary condition is applied at the solid surface. DSMC result is calculated with opensource code Spartan69as a benchmark. Fig. 14 shows the maximum gradientlength-local Knudsen number computed by the analyticalNCCR method.It can be seen from the contour of KnGLLthat the continuum hypothesis is not valid inside the stand-off shock and near the solid surface of the rear of the sphere,where KnGLLexceeds the critical value of 0.05. It is generally believed that N-S equation cannot obtain accurate predictions in these regions.

Table 4 Computation time per step of each selected case.
Fig. 13 Structured cell distribution.

Table 5 Calculation parameters for supersonic flow past a sphere.
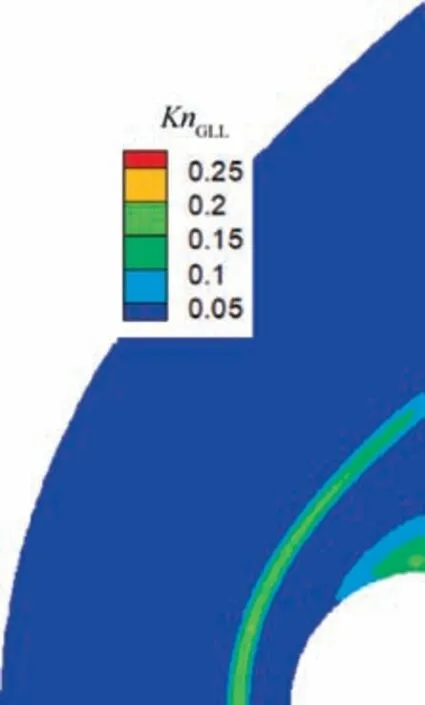
Fig. 14 Contour of gradient length local Knudsen number.
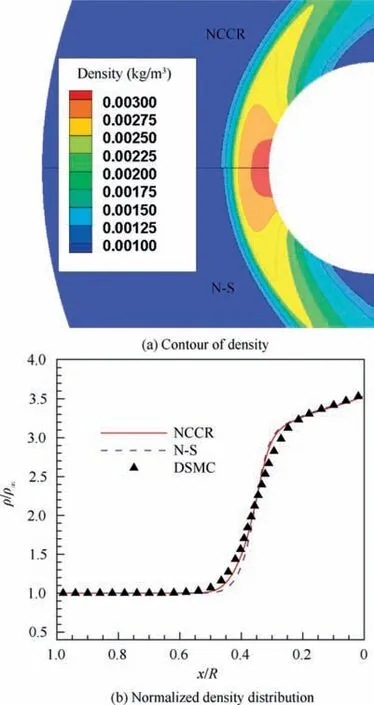
Fig. 15 Contour of density and normalized density distribution along normalized stagnation line predicted by N-S equations and analytical NCCR method (DSMC result is calculated with opensource code Spartan69).
Comparison of the density and temperature between N-S equation and the analytical NCCR method is made in Figs.15 and 16, respectively. It is shown that the shock thickness predicted by the analytical NCCR method is slightly thicker than that by the N-S equation.Also,the shock stand-off distance is larger from the analytical NCCR method compared to the N-S equation. These predictions agree with each other in terms of the KnGLLdistribution in Fig. 14 as the flow regions inside the shock wave are far from the thermodynamic equilibrium.Also, the normalized temperature and density distribution along the normalized stagnation line evaluated by DSMC,N-S and the analytical NCCR method are plotted for further analysis in Figs.15 and 16.One feature which should be highlighted is that the analytical NCCR method shows better agreement with DSMC data in terms of density and temperature at the stagnation line. Nevertheless, there are still some differences between DSMC and the analytical NCCR method near the shock wave. It may imply that some key features are not included in the analytical NCCR method when it is simplified from Eu’s generalized hydrodynamic equations.
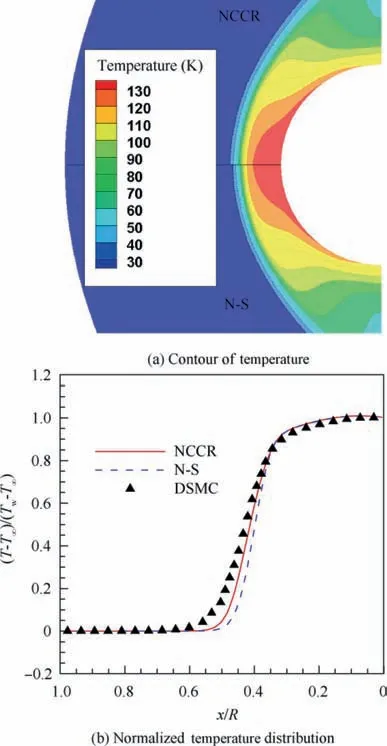
Fig. 16 Contour of temperature and normalized temperature distribution along normalized stagnation line predicted by N-S equations and analytical NCCR method (DSMC result is calculated with opensource code Spartan69).
5. Conclusions
To overcome the deficiency of traditional iterative method in solving NCCR model, an analytical method is proposed by expanding and truncating the nonlinear factor in decomposed solvers to predict nonequilibrium rarefied flows.Without iterative procedure, analytical method is more efficient and preserves the capability of describing non-equilibrium flows in NCCR.To validate its efficiency and accuracy,numerical cases including one-dimensional shock wave structures, Couette flow, two-dimensional hypersonic flows around a cylinder and three-dimensional supersonic flow around a sphere are employed.The results of these cases show that both analytical method and iterative method yield better agreement with experimental and DSMC data in non-equilibrium flows compared with continuum N-S equations. More importantly, the noniterative feature of the proposed analytical method reduces the computational time considerably in both decomposed solvers, which could make NCCR method be a promising engineering tool for modelling rarefied non-equilibrium flows.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Nos.: 11502232, 51575487,11572284, and 6162790014). Zhiqiang HE gratefully acknowledges the support by the China Scholarship Council (No.201906320279). The computational work for this article was partially performed on resources of the National Supercomputing Centre, Singapore (https://www.nscc.sg).
Appendix A. Roots formula for general quartic equation
The four roots x0,x1,x2and x3for the general quartic equation

Appendix B:. Roots formula for general cubic equation
The three roots x0,x1and x2for the general cubic equation are given in the following formula:
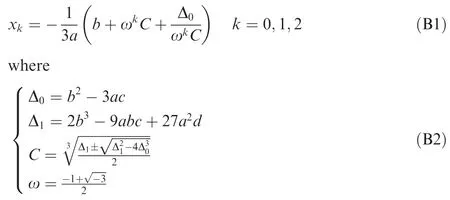
 CHINESE JOURNAL OF AERONAUTICS2021年2期
CHINESE JOURNAL OF AERONAUTICS2021年2期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Recent active thermal management technologies for the development of energy-optimized aerospace vehicles in China
- Electrochemical machining of complex components of aero-engines: Developments, trends, and technological advances
- Recent progress of residual stress measurement methods: A review
- Micromanufacturing technologies of compact heat exchangers for hypersonic precooled airbreathing propulsion: A review
- Towards intelligent design optimization: Progress and challenge of design optimization theories and technologies for plastic forming
- A combined technique of Kalman filter, artificial neural network and fuzzy logic for gas turbines and signal fault isolation
