Suppressing nonlinear aeroelastic response of laminated composite panels in supersonic airflows using a nonlinear energy sink

Jin ZHOU, Minglong XU, Zhichun YANG, Yingsong GU

a State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace Engineering, Xi’an Jiaotong University, Xi’an 710049, China

b School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China

KEYWORDS Aeroelasticity;Laminated composite panel;Nonlinear dynamics;Nonlinear energy sink;Panel flutter;Passive suppression

Abstract This paper proposes using a Nonlinear Energy Sink (NES) to suppress the nonlinear aeroelastic response of laminated composite panels in supersonic airflows. Relevant aeroelastic equations are established using Hamilton’s principle and a finite element approach, drawing upon Von Karman’s large deflection theory and first order piston theory. The idea of the NES suppression region is proposed and the effects of NES parameters on the NES suppression region are studied in detail. The results show that the nonlinear aeroelastic responses of the panel can be completely suppressed by the Transient Resonance Capture(TRC);the appropriate NES parameter values can increase the critical dynamic pressure for flutter and suppress the nonlinear aeroelastic response effectively.Increasing the mass ratio of the NES can improve the NES suppression region;the nonlinear stiffness coefficient and damping of the NES within a specific range can suppress the nonlinear aeroelastic response. The most effective installation position for a NES is in a specific region behind the center-line of the panel in the direction of the airflow.

1. Introduction

Panel flutter can be described as a self-excited oscillation of the external skin panel of a flight vehicle where one side is exposed,usually, to a supersonic or hypersonic airflow.1,2Because of the geometric nonlinearity caused by large deformation of the panel structure, panel flutter usually presents as a limited amplitude vibration. Continuous panel flutter may cause fatigue damage of panel structures and can even lead to flight accidents.3To reduce the possibility of panel fatigue damage caused by aeroelastic problems, the critical dynamic pressure for flutter needs to be increased or the aeroelastic response of the panel needs to be suppressed for small amplitudes.Over the past few decades,a lot of research has been devoted to the active control of panel flutter using smart materials.4–10It has been proved that active control technology has the ability to suppress the aeroelastic response of panels. However, it requires the addition of actuators and sensors, and delays in signal transmission can reduce the performance of the control system, or even lead to instability in closed-loop systems. Passive vibration control avoids these kinds of problems and has the advantages of good robustness and no energy consumption. A number of researchers have therefore looked at using it to suppress panel flutter.11–13

In this paper, a new passive control strategy is proposed,where a Nonlinear Energy Sink (NES) is used to suppress the aeroelastic response amplitude of a panel. The NES comprises a small mass, a linear damper and a nonlinear spring that are attached to the panel at a predetermined position.Unlike linear dynamic absorbers,which are only effective over a narrow frequency band, a NES is effective across a broad range of frequencies because of its nonlinear stiffness.14The NES has mostly been studied in lumped parameter systems associated with coupled oscillators.15–18After in-depth study in such systems, the NES is applied to vibration suppression in continuous structures.19–23Recently,The NES has also been applied to flutter suppression in aeroelastic wing systems. Lee et al.24,25,for instance,pointed out the effectiveness of using a NES for wing flutter suppression using both theoretical and experimental studies.This work also used time-frequency analysis and energy-frequency analysis to identify the mechanism associated with wing flutter suppression using a NES. Bichiou et al.26has found that a NES can reduce pitch and plunge amplitudes,but this reduction is limited to a very small region of the freestream velocities above the flutter speed. Ebrahimzade et al.27compared the effects of linear and nonlinear dynamic vibration absorbers on the flutter stability boundary and nonlinear flutter response of wings. Yan et al.28applied a NES to transonic wing flutter suppression and found that a NES may cause a wing to exhibit Limit Cycle Oscillations(LCO) at its new equilibrium position. Zhang et al.29studied the vibration response mechanism at different velocities of a two-dimensional wing with a NES attached to its front and rear edges.Guo et al.30used a NES to suppress the aeroelastic response of an airfoil with control surface freeplay in an incompressible flow.

The NES has also been used to suppress the aeroelastic response of panels in supersonic airflows. Zhang et al.31applied a NES to an aeroelastic plate model and outlined how this technique can be used to reduce the time required for the panel to return to static equilibrium after perturbations. However, this study only investigated pre-flutter conditions. Pacheco et al.32provides important insights on the mechanism through which a NES can either suppress flutter or mitigate LCOs by partially balancing the aerodynamic work. However, only a few discrete dynamic pressures were used to illustrate the effectiveness of a NES on suppressing flutter in an isotropic panel. Some unique nonlinear dynamic behaviors,such as the phenomenon of transient resonance capture, were not obtained for the panel-NES aeroelastic system.In addition, the bifurcation characteristics and the effects of NES parameters on the NES suppression region were not studied in the previous literatures.

Composite laminated panels are increasingly being used in aerospace construction because of their weight efficiency,high strength-to-weight ratio, ease of design and excellent energy absorption characteristics. In this work, the focus is therefore upon the nonlinear aeroelastic response of laminated composite panels with a NES in supersonic airflows.In particular,the paper provides a detailed examination of the effects of NES parameters on the bifurcation characteristics and NES suppression regions of laminated composite panels with a NES.

2. Nonlinear finite element formulation

Fig.1 is a schematic diagram of an aeroelastic model of a 3-D panel with a NES. The system comprises a NES with pure cubic stiffness nonlinearity and the panel the NES is installed on.a,b and h are the length,width and thickness of the panel,respectively.mnes, knesand cnesare, respectively, the mass, nonlinear stiffness coefficient and damping of the NES. （xs，ys） is the installed position of the NES.

2.1. Constitutive equations

A MIN3 plate element with improved transverse shear, developed by Tessler and Hughes,33was extended and used in this study.It is assumed that for small in-plane strains and moderately large transverse displacements, the von Karman nonlinear strain-displacement relationship can be given by:

εmis the linear membrane strain vector; εmbis the nonlinear membrane stretching strain vector due to a moderately large deflection;and κ is the bending curvature vector.Each of these can be given by the following:

In the general case of composite lamina, the constitutive relations for a laminated composite panel can be expressed as follows:

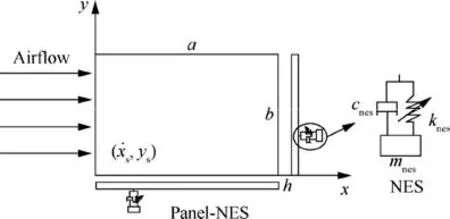
Fig. 1 Aeroelastic model of a 3-D panel with a NES.

Nlis the total number of layers. A, B, D and Asare the laminate extensional, coupling, bending and shear stiffness matrices, respectively.

2.2. Quasi-steady first-order piston theory aerodynamics

For panel flutter in supersonic airflows, quasi-steady firstorder piston theory can usually be employed.1,2The aerodynamic load can be expressed as:

2.3. Governing equations

When deriving the finite element equations of motion for a laminated composite panel with a NES,the Hamilton principle can be adopted:

3. Verification

To validate the proposed approach, aeroelastic response results for simply supported square isotropic and square[0/45/-45/90]spanels were obtained and compared to other results in the literatures,as shown in Fig.2.It can be seen that there was excellent agreement between the results of the present study and the results given in Ref.34.In addition,the time history responses for a fully-clamped square isotropic panel with and without a NES in Ref. 32 were calculated using the proposed approach at λ=1000, as shown in Fig. 3(a). The response amplitudes with and without a NES were, respectively, 0.65 and 0.42. These results are consistent with the results in Ref.32,as shown in Fig.3(b).Based on the analysis,the proposed approach can be used to analyze the nonlinear aeroelastic responses of laminated composite panels with a NES in the supersonic airflow.

4. Results and discussion

A simply supported square graphite/epoxy panel of eight layers [90/0]2sis used as a research object. The dimensions of the panel are a=0.305m, b=0.305m and h=0.00127m.The material properties of the panel are E1=155 GPa,E2=8.07 GPa, G12=4.55 GPa, G23=3.03 GPa, υ12=0.22 and ρ=1550 kg/m3. To obtain the Limit Cycle Oscillation(LCO)response accurately,convergence without a NES across different modes is studied first, as shown in Fig. 4. It can be seen that the LCO response obtained using 16 modes offered the same level of accuracy as that using 24 modes.The first 16 modes are therefore used to analyze the LCO response of the laminated composite panel with a NES, as presented below.

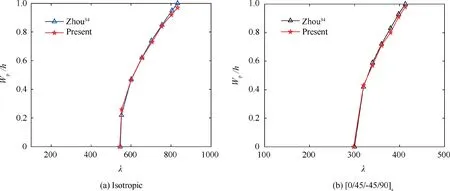
Fig. 2 Comparison of limit-cycle amplitudes for a square panel with a simply supported boundary.

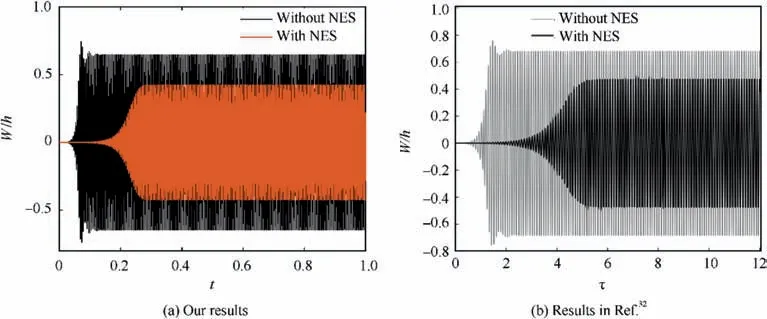
Fig. 3 Time history responses for a fully-clamped square isotropic panel with and without a NES at λ=1000.

Fig. 4 Convergence using different modes

4.1. Nonlinear aeroelastic response behavior

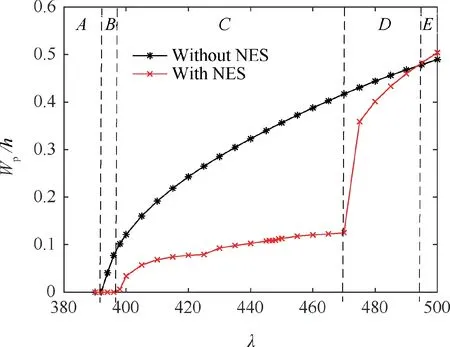
Fig. 5 Bifurcation diagram of aeroelastic responses for a laminated composite panel with and without a NES

For the tests referred to here,the basic parameters of the NES are taken to be=0.1,=0.5 and=5000. Fig. 5 shows the bifurcation diagram of the nonlinear aeroelastic responses for the laminated composite panel with and without the NES.Due to the effect of the NES,the bifurcation diagram in Fig.5 can be divided into five regions. In Region A (λ ≤392), the nonlinear aeroelastic response of the laminated composite panel with or without the NES converges to an equilibrium position.However,the NES can significantly reduce the aeroelastic response amplitude of the laminated composite panel caused by the initial disturbance. See, for instance, the time history response of the laminated composite panel with and without a NES at λ ≤390 in Fig. 6(a). In Region B(392<λ ≤396), the response of the laminated composite panel without a NES exhibits a stable LCO,but the laminated composite panel with a NES converges to an equilibrium position, such as in Fig. 6(b) at λ=396, which shows that a NES can increase the critical dynamic pressure for flutter.In Region C (396<λ ≤470), the response amplitude of the laminated composite panel with a NES is noticeably smaller than that without a NES, which indicates that a NES can suppress the flutter response of laminated composite panels effectively.This region can be considered as a unique nonlinear response region due to the NES, which can be named the NES suppression region. In addition, the phenomenon of Transient Resonance Capture (TRC) is obtained, which is not found for the panel-NES aeroelastic system in the previous literatures, such as in Fig. 6(c) at λ=460. With an increase of dynamic pressure, a sudden jump appears and the aeroelastic responses of the laminated composite panel enter into Region D(470<λ ≤494), where the aeroelastic response amplitude of the laminated composite panel with a NES is still smaller than that without a NES. However, the suppression effect of the NES is obviously weakened as a result of the increase of dynamic pressure. When λ>494 (Region E), the response amplitude of the laminated composite panel with a NES is larger than that without a NES,which indicates that,above a certain dynamic pressure,the NES loses the suppression effect on the nonlinear aeroelastic response of laminated composite panels. Figs. 6(d) and (e) show the time history responses of the laminated composite panel with and without a NES at λ=485 and λ=500, respectively.

In general, the NES can increase the critical dynamic pressure for flutter and suppress the nonlinear aeroelastic response of a laminated composite panel effectively in a certain range of dynamic pressure above critical dynamic pressure. As the dynamic pressure increases to a certain value,the NES will lose its suppression effect.

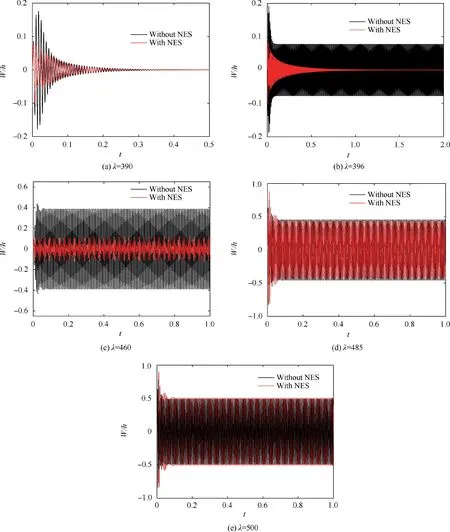
Fig. 6 Time history responses of the laminated composite panel with and without a NES

4.2. Mass ratio effect

To study the effect of the mass ratio,the bifurcation diagrams of the laminated composite panel responses are examined for different mass ratio values while the other three parameters are fixed. Fig. 7 shows the resulting bifurcation diagrams for flutter responses with and without a NES. It can be seen that,when the mass ratio is small,the NES not only fails to suppress the aeroelastic response of the laminated composite panel,but also,in fact,makes the response amplitude bigger.As the mass ratio increases, the NES gradually plays a role in suppressing the nonlinear aeroelastic response and the NES suppression region increases accordingly. Fig. 8 shows the effect of different mass ratios on the maximum amplitude of the response at λ=405 and λ=420, respectively. It can be seen that, for a fixed dynamic pressure, when the mass ratio increases, the aeroelastic response amplitude will change suddenly at a certain point.Prior to this point,the NES has little or no suppression effect,but,after it,the NES begins to suppress the flutter response of the panel effectively.At a higher dynamic pressure,there is a similar sudden change in relation to the mass ratio,which is larger than it is for a small dynamic pressure.

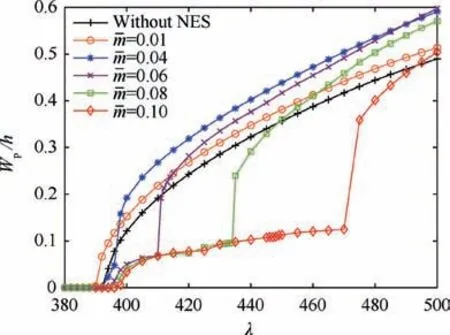
Fig.7 Bifurcation diagram of laminated composite panel flutter response with and without a NES for different mass ratios

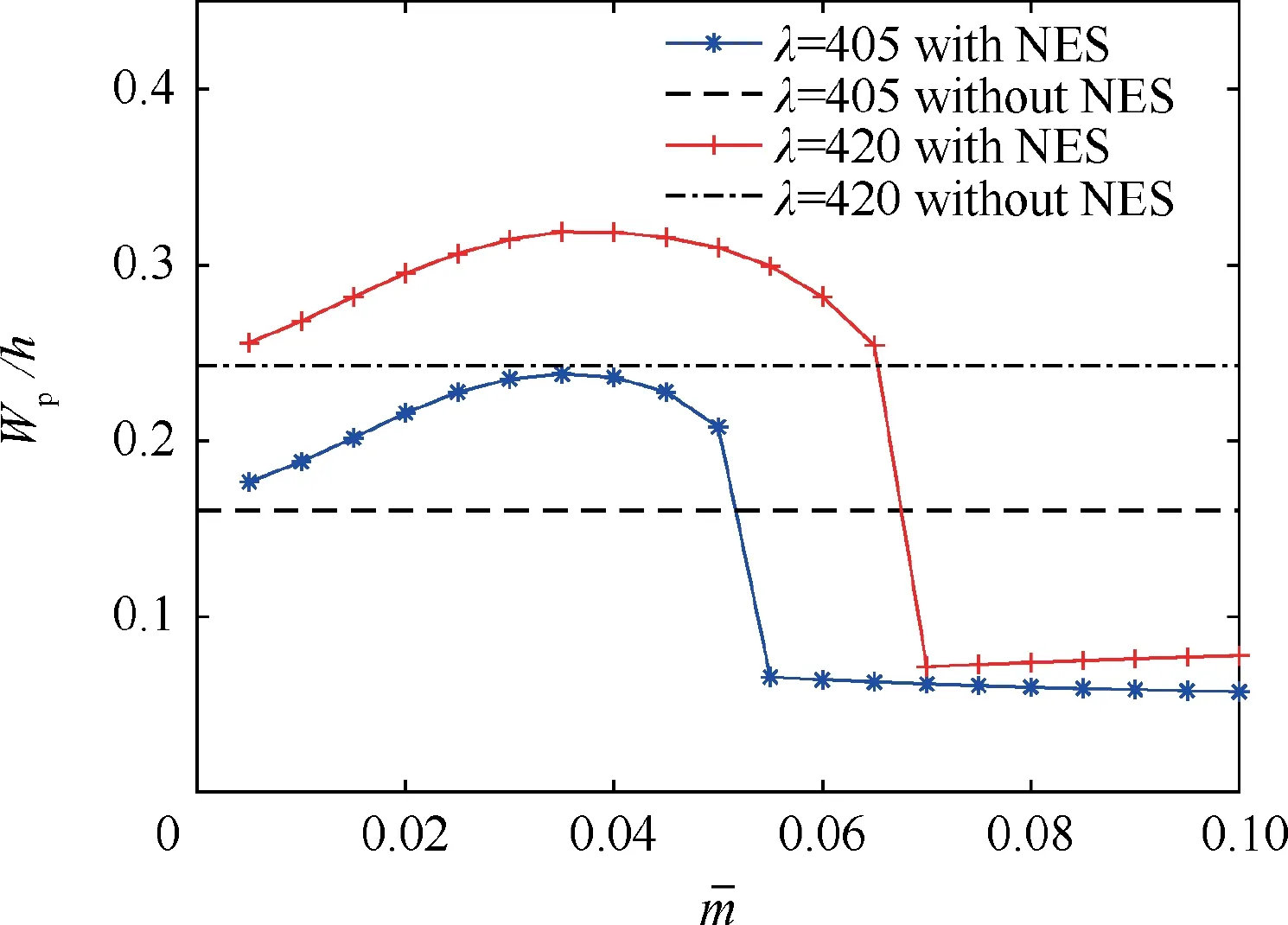
Fig. 8 Effect of mass ratio on the maximum amplitude of the response at λ=405 and λ=420.

4.3. Nonlinear stiffness coefficient effect

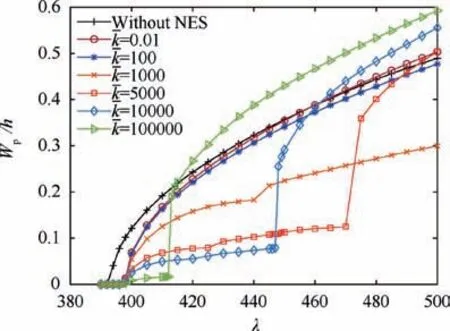
Fig.9 Bifurcation diagram of laminated composite panel flutter response with and without a NES for different nonlinear stiffness coefficients

Fig. 9 shows the bifurcation diagrams for the laminated composite panel flutter response with and without a NES for different nonlinear stiffness coefficients. It can be seen that,when the nonlinear stiffness coefficient is small, the NES is not very effective at suppressing the panel flutter response,although the response amplitudes of the panel with a NES does reduce slightly at a lower dynamic pressure. With an increase of the nonlinear stiffness coefficient, the response amplitudes of the laminated composite panel with a NES are slightly reduced at the lower dynamic pressure, but are significantly reduced at a higher dynamic pressure, such as=1000. However, in practical engineering applications, the response amplitudes would be expected to be significantly reduced at the lower dynamic pressure. When the nonlinear stiffness coefficient is increased to k-=5000, the NES is able to suppress the nonlinear aeroelastic response effectively within the dynamic pressure range described in Section 4.1.When the nonlinear stiffness coefficient continues to be increased, e.g. to=10000, the NES suppression region of the NES is reduced.In general,with the increase of the nonlinear stiffness coefficient, the suppression region first increases and then decreases.Fig.10 shows the effect of various nonlinear stiffness coefficients on the maximum amplitude of the response at λ=405 and λ=420, respectively. It can be seen that, when the nonlinear stiffness coefficient is too small or too large, the NES has little or no suppression effect on suppressing the panel flutter response.So,the NES only has a suppression effect only within a certain range of nonlinear stiffness coefficients.

4.4. Damping effect

Fig. 11 shows the bifurcation diagram for the laminated composite panel flutter response with and without a NES for different degrees of damping. It can be seen that, when there is very small damping, the NES is able to suppress the response of the laminated composite panel effectively under conditions of low dynamic pressure. However, the critical dynamic pressure for flutter at=0.1 is smaller than that at=0.5.When the damping increases, the suppression effect of the NES begins to weaken. Fig. 12 shows the effect of damping on the maximum amplitude of the response at λ=405 and λ=420. Generally speaking, with an increase of damping,the response amplitude of the laminated composite panel decreases initially then increases. This suggests that the NES will lose its suppression effect on the aeroelastic response of a laminated composite panel if the damping becomes too large.

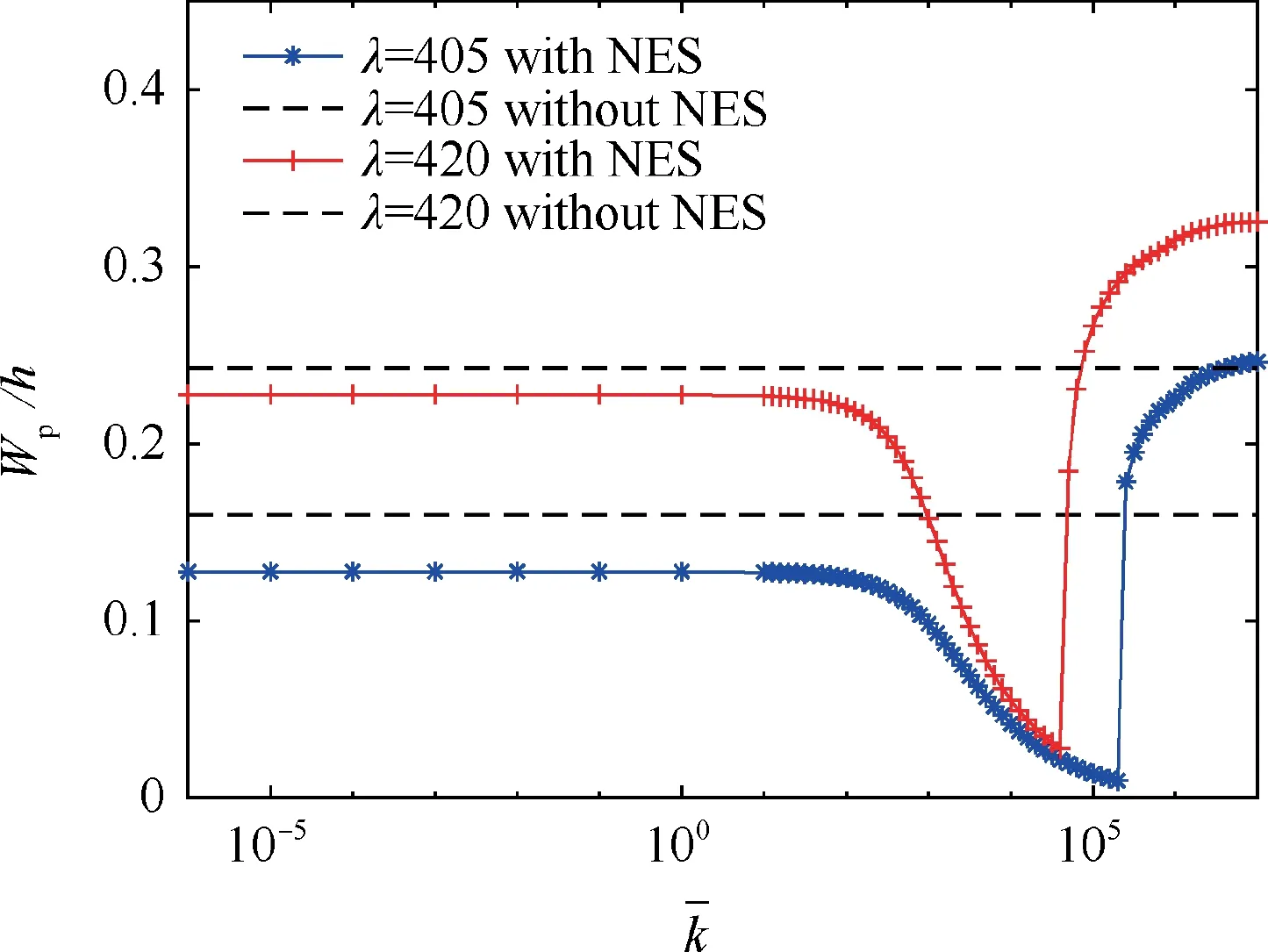
Fig.10 Effect of nonlinear stiffness coefficients on the maximum amplitude of the response at λ=405 and λ=420.

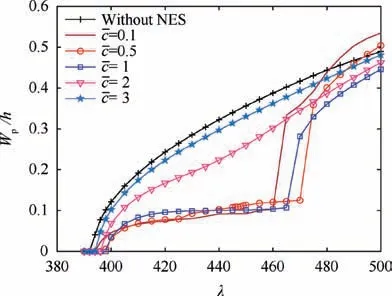
Fig. 11 Bifurcation diagram of laminated composite panel flutter response with and without a NES for different degrees of damping

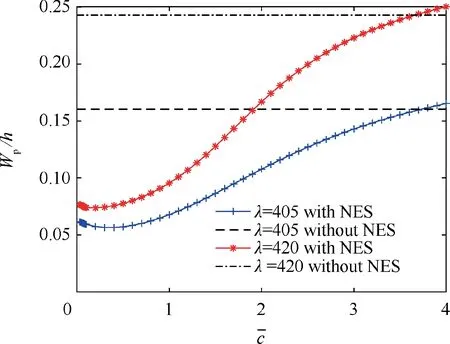
Fig. 12 Effect of damping on the maximum amplitude of the response at λ=405 and λ=420.

4.5. Installed position effect

Fig. 13 shows the finite element mesh used to analyze the aeroelastic response of the laminated composite panel with a NES. The panel is constructed to be symmetrical in the direction of the airflow,so only a few positions along the center-line and in the upper part P1, P2, P3, P4, P5, P6, P7and P8, in Fig.13 are selected as potential installation points for analysis.Fig.14 shows the bifurcation diagrams for the laminated composite panel flutter response with a NES installed at different positions. It can be seen that, when the NES is installed at P1, it has little suppression effect on the response of the laminated composite panel. When it is installed at P2and P3,although it reduces the response amplitude of the laminated composite panel to some extent, the reduction is relatively small.When it is installed at P4,it only has a suppression effect within a small range of dynamic pressures.When it is installed at P5, although the response amplitude of the laminated composite panel with a NES is smaller than that without a NES,the response amplitude remains larger than that without a NES for the range 410<λ<440 which is not expected.When it is installed at P6,the NES has a very good suppression effect.It also has a good suppression effect at P7,within the range of dynamic pressures described in Section 4.1.When it is installed at P8, the NES makes the aeroelastic response worse. To enable the effect of the installation position to be grasped more intuitively, the maximum amplitudes of the aeroelastic response are obtained at λ=420, as shown in Fig. 15, when the NES is installed at each finite element node, respectively.This makes it clear that the most effective installation position for the NES, i.e. where the aeroelastic response of the laminated composite panel can be suppressed most effectively, is in a specific region behind the center-line of the panel in the direction of the airflow.

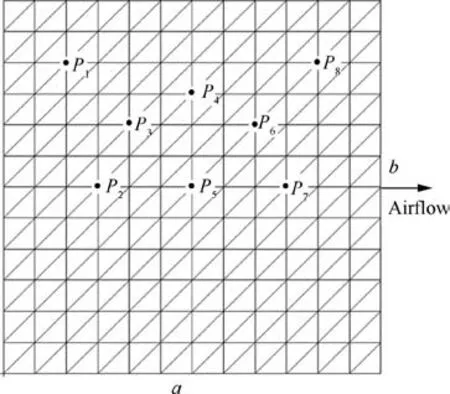
Fig. 13 Finite element mesh

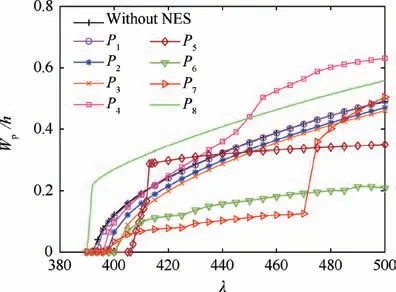
Fig. 14 Bifurcation diagram of laminated composite panel flutter response for a NES installed at different positions

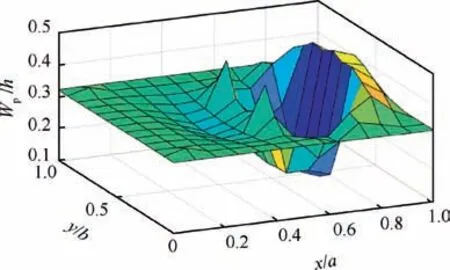
Fig. 15 Effect of the installation position on the maximum amplitude of the response at λ=420.

5. Conclusions

This paper has explored the potential application of a nonlinear energy sink to passively control the nonlinear aeroelastic response of laminated composite panels in supersonic airflows.The effects of NES parameters on the response behavior of laminated composite panels are studied in detail using a finite element based analysis. From the study, the following important conclusions can be drawn:

1) A NES can increase the critical dynamic pressure for flutter and suppress the flutter response of laminated composite panels effectively in a specific range of dynamic pressures. If the dynamic pressure continues to increase beyond this range, the NES will lose its suppression effect.

2) When the mass ratio is relatively small, the NES is unable to suppress the aeroelastic response of the laminated composite panel,and may even make the response amplitude larger.If the mass ratio is increased,the NES will begin to play a more effective role and the NES suppression region will increase accordingly.

3) In general, the NES can suppress the aeroelastic response of laminated composite panels effectively for a specific range of nonlinear stiffness coefficients and degrees of damping. In that case, achieving an optimal suppression effect involves finding a suitable combination of nonlinear stiffness coefficients and damping.

4) The most effective installation position of a NES to be able to suppress the aeroelastic response of a laminated composite panel is in a specific region behind the centerline of the panel in the direction of the airflow.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China (Nos. 11702204, 11872050 and 11672240), the Chinese Postdoctoral Science Foundation(No. 2019M653585) and the Natural Science Basic Research Plan in Shanxi Province of China (No. 2018JQ1041).