Numerical simulation of broken pin effects on the flow field and cooling performance of a double-wall cooling configuration

Wenjing GAO, Honglin LI, Lei LI, Zhe’nan ZHAO, Zhufeng YUE

Department of Engineering Mechanics, Northwestern Polytechnical University, Xian 710129, China

KEYWORDS Broken pin;Computational Fluid Dynamics;Cooling performance;Double wall configuration;Turbine blades

Abstract In this paper, the flow characteristics of the double wall structure are presented and the effect of the broken pin size on the cooling performance and flow field of the double wall configuration is investigated.A periodic plate model with seven units is adopted,and there are an impingement hole and a film hole in each unit. Under five blowing ratios, six different sizes of the broken pin are compared, and the double wall configuration without broken pins is taken as the baseline.The results show that if the broken pins height is too small,the cooling effectiveness usually cannot be improved. With the presence of broken pins with a height of more than 0.4, the effectiveness is improved due to the enhancement of reattachment and recirculation of coolant. With the increase of the broken pin height,the cooling effectiveness increases.However,the increase of the diameter does not always improve the cooling performance, since the limiting effect of the wall jet. In this study,Case 6 with the largest broken pin always has the best cooling performance,but also the largest flow resistance.In Case 6 temperature is reduced by almost 15 K compared to the baseline,and more areas have relatively higher cooling effectiveness.

1. Introduction

As the needs for higher overall efficiency and higher specific power output arises, modern gas turbine systems are required to operate at higher turbine inlet temperature, which has already been far beyond the material acceptable level. As a result, the advanced cooling schemes must be applied in the turbine vane or blade to protect it from thermal stresses. At present, the cooling system of turbines is usually composed of external film/effusion cooling and internal convective/impingement cooling, with which the cooling effectiveness can reach 0.4–0.6.Many studies have been carried out on these traditional cooling structures, such as the studies about film cooling.1However,cooling effectiveness of the current cooling system is heading for an extreme and thus cannot meet the needs of the future gas turbine.In addition,the current cooling system needs a large amount of cooling flow, which is also unfavorable to turbine performance.

Nomenclature

cfflow resistance coefficient

D diameter (m)

H height (m)

Hnheight of narrow cavity (m)

M blowing ratio, ρcUc/ρ∞U∞

m mass flow rate (kg/s)

P Pressure (Pa)

ReDReynolds number of mainstream flow, ρ∞U∞D/μ

RecReynolds number of coolant flow

T temperature (K)

U velocity (m/s)

x stream-wise coordinate (m)

y spanwise coordinate (m)

z coordinate normal to model surface (m)

Greek symbols

η cooling effectiveness, (T∞-Tw)/(T∞-Tc)

μ viscosity (kg/ms)

ρ density (kg/m3)

Θ non-dimensional temperature(T∞-T)/(T∞-Tc)

Subscripts

b broken pin

c coolant

f film cooling hole or target plate

i impingement hole or impingement plate

o out

w wall

∞ gas

ave area-averaged within investigated region

Hence advanced cooling methods are strongly required to upgrade the turbine cooling performance and reduce the cooling air consumption. In recent years, the laminated cooling configuration is believed to be a promising cooling method.It integrates the impingement, the pin, and the film/effusion cooling configuration, as shown in Fig. 1. The structure without pins is called double wall configuration. The coolant jet hits the target surface through the impingement cooling hole and then forms the wall jet. Finally, the coolant is discharged from the film hole and forms the film layer on the outer surface. In addition, the pin-fins can increase the internal contact area and fluid turbulence.The laminated cooling structure was firstly used in combustor cooling. Many researchers studied about the cooling performance of the laminated cooling structure in combustor cooling.2,3Since then,the laminated cooling structure has been applied to other fields. Kim et al.4conducted experiments to compare with the effusion cooling structure and the laminated cooling structure. Rogers et al.5,6developed an experiment facility to study a double wall cooling configuration with cross flow coolant supply. Furthermore,they considered the effect of streamwise development and some parameters of mainstream and coolant. Ignatious and Sarasamma7made a numerical investigation of the impingement/effusion cooling structure for the application in both aircraft combustion liner and electrical power generation.Mensch and Thole8compared the impingement cooling, film cooling,and combination of these two,for the endwall cooling application.

Fig. 1 Schematic diagram of laminated cooling structure.

In recent years, researchers have tried to integrate the laminated cooling into the turbine vane and blade cooling.Besides, the integrally casting of the blade with a laminated structure becomes feasible. For the laminated cooling structure, there are many factors that affect its cooling performance, and mainly are the geometry of the laminates and the element arrangement. There have been several studies around these issues and many kinds of laminated structures are investigated.Some investigations have been made to study the effect of geometric size on the cooling performance.Zhang et al.9made an experimental investigation to analyze the effect of hole spacing on the flow resistance and heat transfer coefficients.Similarly,Zhou et al.10studied the effect of hole spacing on the overall cooling effectiveness and total pressure loss.The film hole has a key effect on the cooling effectiveness of the laminated cooling structure.In Li et al.11the effect of film hole diameter on cooling effectiveness and discharge coefficient was discussed.Wang et al.12and Jung et al.13analyzed the effect of the angle of film hole in the stream-wise direction.And Zhang et al.14compared the film hole cooling performance with the ejection angle in three different directions.

In a laminated cooling structure,since the channel between the impingement plate and the target plate is narrow, the impingement jet turned into wall jets, and there are passage vortices, which is beneficial to the cooling performance. The arrangement of the impingement cooling hole and the gap distance (the distance between the impingement plate and target plate) have a great influence on this phenomenon. Terzis et al.15–19made experimental studies on the narrow impingement channels.They analyzed the effect of hole spacing,channel width, channel height, and et al. Furthermore, they provided three new types of configuration: the channel with hole offsetting from the centerline, the channel with uniform variation in hole diameter,and the channel with varying width.Wang et al.20experimentally investigated the effect of the gap distance and the position of impingement cooling hole on the heat transfer coefficient, with double wall cooling structure.They presented that the gap distance has a great influence on the maximum local Nu,while the heat transfer characteristic is mostly affected by the position of the impingement cooling hole.Funazaki and Hachiya21used a symmetric element model to simulate the flow pattern of laminated structure with the k-ε turbulence model. In addition, they analyzed the effect of pin height and pitch on the heat transfer characteristics and pressure loss.

The element arrangement was a decisive factor in the cooling performance of the laminated cooling structure. Cho and Rhee22compared three different arrangements between the impingement cooling hole and film hole, using the impingement/effusion cooling structure.They found that the staggered hole relative arrangement is better than the other two types.In Tan et al.23,experiments were conducted to compare the adiabatic film cooling effectiveness and the overall cooling effectiveness of two types of double wall cooling configurations,which are staggered arrangement and shifted arrangement separately. The result showed the cooling hole in a staggered arrangement has higher overall cooling effectiveness.However,the effect of the additional impingement hole is more obvious when the holes are designed in inline arrangement.In Yamane et al.24, both experiment and numerical simulation were conducted to consider the effect of pin density on the cooling effectiveness. They used the same layout arrangement while increasing the pin density. Their result indicated that with two different types of pin density, the cooling effectiveness is almost the same. However, the basic specimen has a larger low temperature region than the fine pin density specimen,since the impingement flow is blocked as the number of pins is increased. Similarly, Kim et al.25,26studied the effect of the pin density on the heat transfer characteristic and measured it by Sherwood number. Nakamata et al.27,28designed six layouts of laminated cooling and tested the local cooling effectiveness and area-averaged cooling effectiveness. By comparing different specimens, the influence of hole relative arrangement, additional pin, and pin arrangement were analyzed. The result indicated that, with the same pin density,the cooling effectiveness may be reduced as the pin is too close to the impingement hole. Funazaki and Salleh29tried to analyze the cause of the performance difference in cooling effectiveness between STAG and STAG2 which are used by Nakamata et al.28.On this basis,Siti and Salleh30put forward four new types of pin arrangement and compared them with STAG and STAG2. In recent years, some studies have been made to find better laminated cooling structures.For example,Zhang et al.31brought a novel laminated cooling layout. In Luo et al.32,33, both the double wall cooling structure with dimple and laminated cooling structure with dimple were studied.They found that when the Reynolds number of the coolant is quite large,the dimple can enhance the heat transfer characters of the target plate, which is influenced by the depth and diameter of dimples.

These studies demonstrated the cooling characteristics of the integrated cooling structure and proved that it is expected to be an effective cooling method for ultra-high inlet temperature turbine vanes and blades.However,the current research is limited,and its flow characteristics need to be further analyzed.Moreover, a lot of information about heat transfer, cooling,and pressure loss characteristics of the integrated cooling structure is still needed, in order to better apply it to actual turbines. On the other hand, it is important to control a relatively low flow resistance coefficient while improving the cooling effectiveness. A large flow resistance coefficient means higher aerodynamic loss, which may lead to the failure of the coolant air jet to inject out of the film holes The existence of pin fins in the laminated cooling structure is an unfavorable factor for the control of the flow resistance coefficient.In order to improve the cooling effectiveness of the double wall cooling structure, the attempt is made by adding broken pins on the target plate. Therefore, the objective of the present study is to further analyze the flow characteristics inner the double wall structure, explore the potential improvement of the double wall structure cooling performance through additional broken pins, and analyze the influence of the broken pin on the flow field and cooling performance of a double-wall cooling configuration.In this paper,a flat plate model is used and the cooling characteristics of double wall structures with six different broken pins are present.

2. Geometry model

In this study, the computational domain shown in Fig. 2 is used. The fluid domain consists of two parts: the mainstream channel and the cooling flow channel.The height of the mainstream channel is 8.0 mm, and its width is in accordance with the length of the layout unit. In addition, the mainstream entrance is located upstream of the test model and its distance is 4 times the layout unit length so that the mainstream can be fully developed. Similarly, the mainstream exit is located two times the unit length downstream of the test model. The coolant flow enters the test model from the bottom and the cross section of the cooling channel is the same as that of the test model.

The test model is composed of the impingement plate and the target plate. Six kinds of improved models are studied, in which broken pins are added into the target surface.And they are compared with the test model without the broken pin(Case 0).The unit layout of Case 0 and the improved model is shown in Fig. 3(a) and (b). As shown in the figure, both the effusion holes and impingement holes are arranged in the inline pattern,while their relative arrangement is a staggered pattern. The broken pins locate in the middle of the film hole and the impingement hole. Each unit consists of one film hole and one impingement hole,and four broken pins for the improved model. Each test model contains seven layout units, and each unit is numbered as shown in Fig. 3(c).

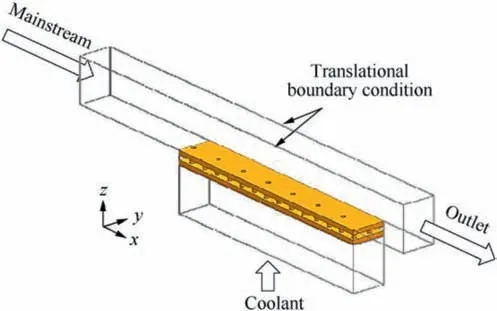
Fig. 2 Computational model.

Fig. 3 Element layout.

The local cross and vertical views of the test model are shown in Fig. 4. The diameters of the film hole (Df) and impingement hole(Di)are all set to be 0.8 mm.The hole spacing of both film hole and impingement hole is 6.0 mm,and the distance between adjacent film hole and impingement hole in stream-wise direction is 3.0 mm. The height of the target plate(Hf)and impingement plate(Hi)are 0.8 mm.The broken pin is located at the midpoint of the connection between each adjacent film hole and impingement hole. The spacing of the broken pin is 3.0 mm. The height (Hb) and diameter (Db) of the broken pin for each model are shown in Table 1.

The thermal conductivity of the test model is set as 10 W/(m·K) and resultant averaged mainstream side Biot number is about 0.1, which is similar to the turbine blade in gas turbines. The velocity inlet boundary condition is set at the inlet of mainstream,the velocity is 500 m/s,the static temperature is 1600 K,and the turbulent intensity is 5%.The Reynolds number of mainstream ReDis kept as 4.8×104. The export of the computational domain is set as the pressure outlet. The coolant inlet is set as mass flow rate inlet: the static temperature of coolant inlet is kept as 800 K,the mass flow rate varies with blowing ratio, and the Reynolds number Recvaries from 1.0×104to 7.7×104. The blowing ratio is defined as:

where ρcUcand ρ∞U∞are derived from the inlet of the impingement hole and mainstream, respectively. While Recis derived from the film hole.

3. Numerical method

The fluid-thermal coupled computations for the problem described above are performed by using ANSYS CFX software. The solutions are obtained by the ensemble-averaged conservation equations of mass (continuity), momentum (full compressible N-S), and energy for a thermally and calorically perfect gas. The advection term in all the conservation equations and turbulence transport equations were discretized by using a high-resolution scheme with second order-accuracy.The residual is less than 10-5and remains stable,for the turbulence quantities.The residual is less than 10-6for the continuity equation,less than 10-6for component velocity equations,and less than 10-7for energy equations.Besides,all converged solutions have a mass imbalance of less than 0.1%.

The overall cooling effectiveness and flow resistance coefficient of coolant are presented and analyzed in detail.The overall cooling effectiveness is defined as:

Fig. 4 Configuration of test model.

Table 1 Geometry parameters of broken pin.

The flow resistance coefficient of coolant is defined as:

3.1. Grid systems

The software ICEM is employed to form the grids for the calculation domains. Grid systems based on hexahedrons are used in the fluid domain because they are known to provide more accurate solutions for flows with boundary layers.While tetrahedral grids are adopted in the solid domain. For Case 0,the number of grids in the solid domain is about 2.055 million,and the number of grids in the fluid domain is about 3.54 million.Fig.5 shows some detailed views of the computation grid.It can be seen that for the fluid domain, grids around the hole is constructed by wrapping grid lines and smooth along the hole side.

The boundary layer y+is between 30 and 100 for the standard k-ε model and RNG k-ε model. However, the boundary layer y+ is less than 1.0 for the standard k-ω model and the SST model. The boundary layer number is more than 15.The growth ratio of the boundary layer is about 1.2 from the walls in all cases. The grid size definition for the identical parts of different turbulence models is the same, except for the boundary layer.

3.2. Solver validation

In order to ensure that the adopted numerical model can well represent the cooling performance of the present model. The simulation results are validated by the experimental data of Nakamata et al.27,28. Two cases of CSHIFT and BASI are selected as the comparison model for the verification and validation of numerical simulation of the double wall structure and the effect of the pin fin. Zhang et al.14and Zhou et al.10also used BASI as the comparison model. The detailed model and boundary condition can be found in Refs.[27,28].In addition,the calculation is carried out with four turbulence models:the standard k-ε model,the RNG k-ε model,the standard k-ω model,and the SST models.The comparisons of area-averaged cooling effectiveness and local cooling effectiveness for computed and measured results27,28are shown in Figs. 6 and 7.The comparison of local cooling effectiveness(Fig.7)shows that the result of the SST model can best reflect the local cooling effectiveness distribution characteristics of the experimental result. Therefore, only the comparison between the result of the SST model and the experimental result is shown in Fig. 6.

The present numerical result can reflect the area-averaged cooling effectiveness as a function of the blowing ratio and can describe the characteristic of the local cooling effectiveness distribution. However, there is a certain error in the quantitative analysis of cooling effectiveness. The error of numerical simulation is mainly due to the prediction of less mixing of jet and mainstream by the eddy-viscosity models. Thereby, at a lower blowing ratio, more coolant spreads to the downstream, and the cooling effectiveness is over predicted, while at a higher blowing ratio, as the coolant jet gradually deviates from the solid surface, more coolant air is injected into the mainstream, and the cooling effectiveness prediction is lower than that of the experiment. In addition, due to less mixing,the deviation of the simulation results of downstream increases slightly.In addition,the uncertainty of the experiment also has some influence on the comparison results. For example, the cooling air temperature at the inlet of the specimen varied from 290 K to 370 K depending on the amount of cooling air flow.In general, the agreement between the numerical simulation result of the SST model and the experimental result is reasonable. Therefore, the SST model with enhanced wall treatment is used in the present simulations, and the following result reported is based on the SST model.

3.3. Grid independence

In order to fully analyze the grid setting of various geometric sizes for our series of research on laminated cooling. A laminated structure was selected for grid-independent research,which is combined by Case 0 and pin-fins. The location of pin–fin is the same as that of the broken pin and the diameter is 0.8 mm. The purpose of grid independence research is to resolve the relevant flow physics and minimize grid-induced errors.Ten grid systems with different grid density were generated, and they were numbered from Grid 0 to Grid 9.

Fig. 5 Local views of computation grids.

Fig. 6 Comparisons of computed and measured area-averaged cooling effectiveness.

Fig. 7 Comparisons of computed and measured local cooling effectiveness at M=0.6.

Grid 0 to Grid 3 is obtained from Grid 0 by adding nodes number of the boundary layer near the wall. Grid 4 to Grid 6 and Grid 2 is obtained by applying h-refinement in the region around film cooling holes, impingement holes, and pin fins.The grid density of Grid 2 and Grid 7 to Grid 9 are adjusted by applying r-refinement in the region around film holes,impingement holes and pin fins.Fig.8 exemplifies grid systems with a h-refined and r-refined grid from the local top view.

The cell numbers and the overall area-averaged temperature of these grid systems are shown in Table 2. And the local area-averaged temperature of these grid systems are shown in Fig.9.It can be seen that Grid 2 with 4.6 million cells can yield the mesh-independent solution,so Grid 2 is selected in the present study.

4. Results and discussion

4.1. Flow field

The double wall structure integrates the impingement cooling structure with the film cooling structure in a narrow cavity.As a result, its internal flow structure is complex and the flow characteristic is different from the traditional large space impingement cooling structure. Therefore, to begin with, the cooling performance and flow filed characteristic of Case 0 are present in detail.

Fig.10 shows the cooling effectiveness distribution of Case 0 under five blowing ratios. It can be seen that the increase of blowing ratio does not significantly influence the shape pattern of overall cooling effectiveness distribution, but its effect on pure film cooling is usually more significant in previous studies. In addition, overall cooling effectiveness in every point is significant enhanced with the blowing ratio increasing,and significantly slow down when M ≥1.0.

Fig. 8 Local top view of h-refined and r-refined grids.

Under each blowing ratio, the overall cooling effectiveness shows an increasing trend along the flow direction in the first few units. It is a typical process for the development of the thermal boundary layer. Due to continuous external cooling,the temperature of the near-wall fluid decreases along the flow direction.Moreover,the heat flux between the mainstream and the external wall decreases along the flow direction with the increase of film thickness on the outer wall. At about the fifth and sixth units (the unit segmentation and numbering are shown in Fig. 3(c)), the unit area-averaged cooling effectiveness reaches the peak value or tends to be stable.The last unit is influenced by the outlet boundary conditions and the end wall behind the impingement hole, so there is a hightemperature region at its trailing edge. This phenomenon can be further shown by the area-averaged overall cooling effectiveness of each unit, as shown in Fig. 11(a). In summary,the region containing Area 5 and Area 6 is selected for the local performance display and area-averaged overall cooling effectiveness calculation in the following result reported. And this region is recorded as the investigated region.

In each unit, the shape pattern of temperature distribution is similar, in addition to the influence of the inlet and outlet boundary. The overall cooling effectiveness reaches a peak value near the stagnation region, but it decreases gradually from the center around. This is because the coolant jet ejects to the target surface through impingement holes, and forms the strongest heat transfer near the stagnation region. Then the coolant flow turns to wall jets, and the heat transfer rate decreases with the increase of the wall jet boundary layer thickness.On the other hand,there is another peak value at the outlet of the film hole, and it develops along the stream wise direction. It is formed by external film protection, as well as the heat transfer between the inner wall of the film hole and coolant flow.

Since there is no disturbing structure inside the narrow cavity, it can be seen that the cooling effectiveness decreases in a ring shape around the stagnation region of the impingement hole.However,the peak shape is also deeply different in some units, which is elongated or shifted. In Area 7, the jet peak region shifts upstream and elongates in the spanwise direction,which is more obvious with the increase of blowing ratio.This is due to the presence of an end wall after the jet and pressure of the upstream jet. At M=0.2 or the first few units, the jet peak region usually towards the downstream compared tothe location of the impingement hole. Due to the presence of the front end wall and the offset of the downstream jet, the peak region in Area 1 is elongated along the flow direction.Nevertheless, the kidney shape distribution, which often occurs in classical impingement cooling due to crossflow,does not appear. This is because there is no significant crossflow or crossflow does not affect the impingement jet direction. The main reasons for the deflection of the jet peak region are as follows: (A)the pressure drop in the mainstream path affects the mass flow rate distribution, and more coolant in the wall jet flows downstream. (B) The heat transfer between the mainstream and the out wall promotes the jet peak region moving towards to the downstream.The influence of these two factors is weakened with the increase of the coolant amount.

Table 2 Overall area-averaged temperature for different grid.

Fig. 9 Local area-averaged temperature of different grids.

Fig. 10 Cooling effectiveness contours for Case 0.

The effect of pressure drop in the mainstream path on mass flow distribution can be presented by the percent of the mass flow rate through each impingement hole and film hole under each blowing ratio,as shown in Fig.11(b).The mass flow rate of the coolant through the upstream film hole is lower than that through the downstream film hole. At M=0.2, the mass flow rate of the coolant air through the film hole of Area 7 is almost six times that in Area 1.As the blowing ratio increases,this non-uniformity of the mass flow rate distribution becomes less evident. When M ≥1.0, this non-uniformity is already small. On the other hand, the distribution of mass flow rate through impingement holes is relatively uniform. The mass flow rate increases along the flow direction only when M=0.2, which shows that the pressure drop in the mainstream path leads to the pressure drop in the narrow cavity.

The uniform distribution of mass flow rate also affects the internal flow field. Fig. 12 shows the velocity vectors on the middle cross-section of the narrow cavity. The velocity vector at M=1.3 is similar to that at M=1.0, therefore it is no shown in this figure. It can be seen that the flow field exhibits a significant asymmetry with respect to the direction of the spanwise. At M=0.2, due to the non-uniform distribution of internal pressure, there is obvious local crossflow between adjacent film holes in Area 5 and Area 6. And the location where the wall jets coming out from adjacent two impingement holes impact with each other is near the trailing edge of the film hole (the impact position is referred to as ‘Impingement-Line’). As the blowing ratio increases, the cross-flow is basically disappeared, and the Impingement-Line moves toward the leading edge of the film hole. In addition, under a larger blowing ratio, two vortexes are formed at the leading edge of the film hole,which is conducive to heat transfer on the target surface.

Fig. 11 Area-averaged cooling effectiveness and mass flow rate for Case 0.

For Case 0, the cooling performance of impingement cooling is higher than the film cooling, which is more obvious under a larger blowing ratio.At a small blowing ratio,the film coverage area extends along the flow direction. However,under a larger blowing ratio,the region of high overall cooling effectiveness is concentrated near the film hole, especially for the downstream film. It is due to the impingement cooling influence is enhanced with the increase of blowing ratio.However,the coolant jet is lifted off under a larger blowing ratio,so the film coverage is poor. As shown by the streamlines, and temperature contours on the vertical section and seven crosscutting planes in Fig.13.Where the seven cross cutting planes are located at 3 mm downstream of each film hole respectively.Along the mainstream direction, due to the increase in the mass flow rate of coolant air and the decline in mainstream pressure, the influence core of coolant jet increases and rises.At farther downstream, the lift-off becomes more significant.

4.2. Influence on cooling performance

Figs. 14 and 15 show the cooling effectiveness distribution at M=0.2. Both overall cooling effectiveness contour plot and cooling effectiveness through Line A and Line B are presented.As mentioned, under the small blowing ratio, the center position of the jet peak region is shifted downstream and it is nearly 0.5 Difrom the stagnation point, as shown in Fig. 15(a). In Area 5, the drop gradient is higher in the upstream of the impingement hole, due to this offset of jet peak region. It also reflects that the mainstream has a great influence on the outer surface cooling performance. On the other hand, there is a significant peak of high cooling effectiveness at the exit of the film hole, followed by a sharp drop. The decrease of cooling effectiveness stops at about 0.85 mm downstream of the exit,and then the cooling effectiveness increases in the flow direction. The peak of the cooling effectiveness is due to the heat transfer between the coolant air and the inner wall of the film hole,and the film formed by the coolant air at the outlet. Then it is affected by the mainstream and falls rapidly.However,because of the increase in heat transfer performance,especially the front side of the film hole, the cooling effectiveness increases downstream. Due to the influence of the mainstream and offset of jet peak region, there is a region of low cooling effectiveness occurs between the impingement hole and its upstream film hole. In Area 6, this phenomenon has been alleviated, because of the pressure from the downstream jet.

After adding the broken pin, the overall cooling distribution shape pattern is similar in all cases. However, the broken pin affects the local distribution,especially for the distribution around the position of the broken pin and the shape of the jet peak.For models with shorter broken pin(Case 1 and Case 2),the cooling performance cannot be effectively improved, even the overall cooling effectiveness of Case 1 becomes lower. In Case 1,the peak value of the high impingement cooling region does not change much, but its area decreases obviously. In addition, the cooling effectiveness does not increase at the position of the broken pin, while the cooling effectiveness decrease at the outer-ring of the broken pin position. It indicates that the broken pin appeared to restrict the expansion of the impingement cooling, due to the limiting of wall jet or increase of thermal resistance of heat conduction. As the Dbis increased (Case 2), the limitation of the high impingement cooling region still exists. However, the cooling effectiveness increases at the position and downstream of the broken pin,especially for the downstream broken pin of the impingement hole. This may be due to the increased heat area and turbulence by the broken pin.

Fig. 12 Velocity vectors in the middle plane of the inner-space.

Fig. 13 Coolant streamlines and temperature contour of Case 0 at M=1.0.

Fig. 14 Cooling effectiveness distribution at M=0.2.

When Hb≥0.4 mm, the cooling effectiveness distribution has an obvious improvement with respect to Case 0. Among them, Case 6 has the best performance, while the differences between other models are little. For Case 3 and Case 5, the cooling effectiveness is mainly improved in the whole region.As the Hbincreases, the limiting effect decreases. In addition,the cooling effectiveness increase at the broken pin position downstream of the impingement hole.As the broken pin diameters increases,both the peak value and the distribution of the cooling effectiveness are improved.The peak value of the high impingement cooing region is increased. This may due to the wall jet hits on the broken pin and reattaches on the target plate. Then a thinner boundary layer is formed, which leads to a better heat transfer performance. On the other hand, the cooling effectiveness increases at the outer-ring of the broken pin position. The broken pin increases heat area and turbulence, resulting in the enhancement of heat transfer. Besides,this may also due to a faster flow rate. With the increase of Db, the broken pins block the flow channel and make it narrower, so the velocity is faster.

Fig. 15 Cooling effectiveness along line at M=0.2.

Figs.16 and 17 show the cooling effectiveness contour plots and the cooling effectiveness through Line A and Line B, at M=0.5.Compared to the distribution at M=0.2,the center of the high impingement cooling region is closer to the stagnation point. The peak region of high impingement cooling region increases as the increase of blowing ratio, but the cooling effectiveness drop gradient around the stagnation point is slightly increased. Similar with the result in Section 4.1, the more uniform the wall jet with the blowing ratio increases.On the other hand, the range of the high cooling effectiveness region at the film hole outlet is expanded and the cooling effectiveness decreases rate becomes smaller, due to the increase of coolant air. However, in the downstream region, the cooling effectiveness continues to decrease. Because the internal flow tends to be uniform as the blowing ratio increases, the downstream heat transfer performance between two film holes will not increases. In addition, the outer film begins to lift off in the downstream region.Due to the change of center of the high impingement-cooling region and the concentration of film cooling in the upstream. The low cooling effectiveness region between the impingement hole and its upstream film hole is reduced, while the low cooling effectiveness region between the impingement hole and its downstream film hole is increased.

At M=0.5, the effect of additional broken pins is different.When Hb=0.2 mm,the negative effect of additional broken pins is more obvious. The cooling effectiveness decreases more outside of the broken pin. In addition, the peak value of the high impingement cooling region also decreased. It can be seen that the restriction of the jet expansion on the target plate by the broken pin is greater,which may further affect the thickness of the boundary layer in the high impingement cooling region.When the diameter of the broken pin is larger,the cooling effectiveness decreases and the limiting effect becomes more serious. For models with higher broken pins,the performance improvement is not as obvious as that at small blowing ratio, except Case 6. For Case 3 and Case 5,the cooling effectiveness is still mainly improved wholly.However,in Case 4 it still presents the limiting effect of the broken pin on the wall jet.It can be seen that,when there is no global cross flow inside the narrow cavity, the limiting effect of broken pins plays a greater role in the cooling performance. This may be further validated by the following studies.

The cooling effectiveness distribution in the larger blowing ratio is shown in Figs.18 and 19.Since the effect of the broken pin at the larger blowing ratios are similar, only the cases at M=1.3 is shown. The local cooling effectiveness through Line A and Line B, at larger blowing ratios, are shown in Fig.20.At a larger blowing ratio, the high impingement cooling region has a tendency to upstream, and the cooling effectiveness drop gradient around the stagnation point is stable under each blowing ratios.The film cover region concentrated near the exit of the film hole, and the cooling effectiveness decrease more sharply with the increase of blowing ratio. This is due to the lifting of the coolant of the solid surface. Then,the effect of coolant film is very small and the cooling effectiveness becomes stable. Finally, a local peak of cooling effectiveness appears on the front of the film hole,which is because the suction effects of film holes make the boundary layer thinner in this area and increase the heat transfer intensity. Due to the change of impingement cooling and film cooling performance at larger blowing ratios, the low cooling effectiveness region appears downstream of the film hole.The film hole inclination angle can be added to improve the film cooling performance,or the arrangement can be adjusted to get better ‘‘cooperate”of two cooling techniques.

For the broken pin with a small height, it is more obvious that the effect of broken pin on the internal flow field has a greater impact on the cooling performance. Case 1 has some improvement at cooling performance, but Case 2 with larger heat transfer area has lower cooling effectiveness than Case 0. This is due to the limiting effect of the larger diameter broken pin. Under larger blowing ratio, the addition of higher broken pin improves the cooling effectiveness more, but the influence of Hband Dbis similar to that at M=0.5. In addition,with the increase of blowing ratio,the local cooling effectiveness improvement mainly appears between the impingement hole and its upstream film hole.

Because the effect of the blowing ratio is much larger than the structural difference.Result data are presented in the table to show the differences in cooling effectiveness and flow resistance coefficients in more detail. Table 3 shows the areaaverage cooling effectiveness in the investigated region and the flow resistance coefficient of the structure.

By adding the broken pin,the turbulence of flow increases,and the heat transfer thermal resistance of the surface is reduced, which is conducive to improving the cooling performance. However, it also leads to an increase in thermal resistance of heat conduction. In addition, its effect on the flow field is complex. It can be seen from Table 3 that the addition of broken pins does not always improve the cooling performance, and the cooling effectiveness is not always higher with a larger broken pin. Under the studied blowing ratio, Case 6 has the largest cooling effectiveness, and its temperature decreases are always above 10 K compared with Case 0.

Fig. 16 Cooling effectiveness distribution at M=0.5.

Fig. 17 Cooling effectiveness along line at M=0.5.

With the addition of a small height broken pin,the cooling performance usually cannot be improved. The cooling effectiveness increases with the increase in Hb. However, this enhancement is usually weak, for broken pins with a small diameter. The influence of Dbon cooling effectiveness is more complex. At M=0.2, the enhancement of heat transfer area and turbulence intensity is greater, which is more similar to the effect of pin–fin in large space.Therefore,the cooling effectiveness is higher with the increase of Db. When the blowing ratio increases, the cross-flow in the channel disappears, while there are passage vortices in the channel because of the structural characteristics. The effect of the broken pin on the internal flow field has a greater effect on cooling performance.Therefore, under a larger blowing ratio, the larger diameter may not conducive to the improvement of cooling effectiveness, due to the limiting of wall jets.

The influence of the broken pin on the flow resistance varies with different blowing ratios,due to the differences in internal flow characteristics.With the addition of broken pins,the flow resistance coefficient increases because the wall jet hits on the broken pin.However,the limitation of the broken pin on wall jets leads to the decrease of internal flow velocity,which is beneficial to the reduction of the flow resistance coefficient. At M=0.2, the flow resistance coefficient decreases with the addition of broken pins, which may be due to the decrease of the flow velocity in the channel. The flow resistance coefficient increases as Hbincreases. But the flow resistance coefficient is smaller when Dbis greater. As the blowing ratio increases, the flow resistance coefficient is larger than that of Case 0, due to the blockage effect of broken pins. The flow resistance coefficient still increases when Hbis greater, except Case 1.The flow resistance of Case 1 is larger than that of Case 2,and the difference increases with the increase of the blowing ratio. It is probably due to the smaller decrease in the internal flow velocity in Case 1.While the influence of diameter on flow resistance coefficient is small when Hb≥0.4 mm. In addition,for structure with the additional of pin-fins,the flow resistance coefficient is greatly increased.It is about 0.05 larger than Case 0, which is about 2–5 times the flow resistance coefficient increase caused by the broken pin.

Fig. 18 Cooling effectiveness distribution at M=1.3.

Fig. 19 Cooling effectiveness along line at M=1.3.

Fig. 20 Local cooling effectiveness through Line A and Line B (M=1.0–1.6).

Table 3 Area-averaged effectiveness of investigated region.

Fig. 21 Streamlines velocity magnitude distribution and non-dimensional temperature distribution on sections.

Fig. 21 (continued)

4.3. Influence on flow filed

In order to investigate the effect of additional broken pins on the flow field of the double wall structure, a detailed analysis was made for the calculation of a double wall structure and six cases with different broken pins, under the condition of M=1.0.Fig.21 shows the streamlines and contours of velocity magnitude on tangential sections of the fluid domain, as well as non-dimensional temperature counters on sections of the solid domain. The location of each section is defined as shown in the figure.In A-A’section,the mainstream flows into the page obliquely from left to right.While in B-B’section,the mainstream direction is slanting out of the page from left to right. In the sections of C-C’ and D-D’, the mainstream flow direction is from left to right.

As mentioned above, the cross-flow and passage vortices caused by the uneven pressure distribution cannot affect the impingement jet direction.And the impingement jet is perpendicular to the target plate. Even at M=0.2, the pressure distribution is more uneven,but the jet direction is not affected.It is not shown separately. After hitting the target surface, the coolant flow stagnates and forms wall jet. And the boundary layer of the wall jet becomes thicker. On the other hand, due to the collision of wall jets, a part of coolant fluid recirculates to the target surface or upstream side of the impingement flow.Thus results in an intensive mixing, and forming a region of larger velocity.

The addition of broken pins makes the coolant flow recirculates earlier, thus creating a new vortex. For the coolant from the upstream impingement hole, a vortex is formed before the broken pin. While for the coolant from downstream impingement hole,there is a pair of reverse vortex in front of the smalldiameter broken pin,and a recirculating vortex as the diameter increases. The compression of the broken pin against the vortex is beneficial to the recirculation of coolant flow to the impingement jet.When the Hbis small,the position of the vortex is closer to the broken pin, which cannot effectively promote the recirculation of coolant. Therefore, the heat transfer enhancement in the stagnation region is very small.In addition, at the front of the broken pin, a lowtemperature region is formed by the impact of wall jets. For Case 1 and Case 2, the cooling at this low-temperature region is also very small.As the Dbincreases,the position of upstream recirculation is too low. Therefore, the coolant air cannot rejoin the impingement jet, which weakens the heat transfer in the impingement stagnation region. Moreover, the larger diameter increases the resistance of heat conduction, so the cooling effectiveness at downstream of the broken pin decreases.

As the Hbincreases, the vortex intensity increases, which makes more coolant air rejoin the wall jet. For Cases 3–6,the temperature of the impingement stagnation region decreases, and the maximum temperature drop is nearly 20 K. In addition, as the increase in Hb, a better surface jet is formed after the wall jet hits on the broken pin, and the direction of surface jet velocity is closet to the wall.This makes the temperature of the leading edge of the broken pin decrease obviously,and the temperature drop exceeds 25 K.It is helpful to improve the cooling effectiveness between the broken pin and the film hole. The vortex formed between the broken pin and downstream impingement hole is closer to the surface of the target and broken pin.It benefits the improvement of local heat transfer in this region.And with the increase of the blowing ratio, this phenomenon is more obvious. As shown in Fig. 21, in Case 6, the cooling effectiveness locally between the film hole and its downstream impingement hole.Although when the Dbis larger, the heat conduction resistance increase which weakens the cooling performance enhancement.In Case 6, the increase of vortex intensive eliminates this disadvantage.

Because the broken pin with the same diameter has the same effect on the cross-sections of C-C’and D-D’,only Case 5 and Case 6 are presented.On the C-C’section,due to the influence of geometrical structure, the position of wall jets collision is shifted to upstream. The recirculation near the downstream is smallerandthereiscross-flownearthedownstreamimpingement hole.AstheDbissmall,theadditionofbrokenpinshaslittleinfluence on the flow field between two impingement holes.However,for a larger broken pin, the vortex insensitive enhance which affects the flow direction.As shown in Fig.21(d),the addition of broken pins has little effect on the film jet.However,with the addition of broken pins, the internal velocity distribution becomes uneven,and the velocity increase.

5. Conclusions

In this study, attempts to improve the cooling performance of double wall configuration by adding broken pin were conducted.The cooling performance and flow field characteristics of broken pin configuration were investigated. And six different sizes of broken pins were compared under five blowing ratios. The following conclusions can be drawn.

(1) As the blowing ratio(M)increases,cooling effectiveness is significantly enhanced,and slow down when M ≥1.0.There is a typical process for the development of the thermal boundary layer in the front zone of configuration. In each unit, the highest cooling effectiveness locates around the jet stagnation region,while the influence area of the film cooling flow is mainly in downstream of the film hole along the flow direction. Due to the non-uniform distribution of the wall jet, there is an asymmetry in the internal flow field, especially at small blowing ratios, there is obvious cross flow inside the narrow cavity.

(2) With the addition of a small height broken pin,the cooling effectiveness usually decreased. Because the small height broken pin cannot effectively enhance the vortex intensity and coolant air recirculation. Moreover, if Db=1.2, not only the thermal resistance of heat conduction increases but also the wall jet is limited. Similarly, cooling effectiveness of the double wall configuration with additional hemispherical protrusion(D=1.2 mm) is lower than that of Case 0. This structure is not shown in detail in this paper.

(3) The addition of a broken pin with a height above 0.4 mm can improve the cooling performance of double wall configuration. At M=0.2, the increase in the heat transfer area has a greater influence. While at larger blowing ratios, the influence on the internal flow field plays a greater role in cooling performance. Increasing the Hbcan result in an increase in cooling effectiveness,but also lead to a higher flow resistance coefficient.And the cooling difference between Hb=0.6 and Hb=0.4 is small. The increase of Dbmay lead to the limitation of the wall jet and the increase of heat conduction thermal resistance,so it does not always improve the cooling performance. Under the studied blowing ratios, Case 6 has the largest cooling effectiveness and more uniform distribution of cooling effectiveness.

In general,cooling effectiveness can be improved by adding broken pins.But this beneficial effect is not unlimited,and the influence of geometric size is complex and different from that in classical large space pin–fin cooling. The broken pin needs to be high enough (greater than 0.4 in this paper). Under the studied blowing ratios,Case 6 has the highest cooling effectiveness and more uniform distribution of cooling effectiveness,while the broken pin with Hb=0.4 can provide more balanced cooling effectiveness and flow resistance.The best diameter changes with the situation and the best diameter of the larger column height are larger.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 51975471), Aviation Power Foundation of China (No. 6141B090319), Natural Science Basic Research Plan in Shaanxi Province of China (No.2018JM5173),National Natural Science Foundation of China(No.51975471),National Science and Technology Major Project(2017-VIII-0003-0114)and Natural Science Foundation of Shaanxi Province (No. 2018JQ5041).