Phase plane design based fast altitude tracking control for hypersonic flight vehicle with angle of attack constraint
Yng LIU, Choyng DONG,*, Wenqing ZHANG, Qing WANG
a School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China
b School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China
KEYWORDS Adaptive control;Angle of attack constraints;Barrier Lyapunov function;Hypersonic flight vehicle;Phase plane design;Reaching law design
Abstract In this paper,fast setpoint altitude tracking control for Hypersonic Flight Vehicle(HFV)satisfying Angle of Attack (AOA) constraint is studied with a two-loop structure controller, in the presence of parameter uncertainties and disturbances. For the outer loop, phase plane design is adopted for the simplified model under Bang-Bang controller to generate AOA command guaranteeing fast tracking performance. Modifications based on Feedback-Linearization (FL) technique are adopted to transform the phase trajectory into a sliding curve. Moreover, to resist mismatch between design model and actual model, Fast Exponential Reaching Law (FERL) is augmented with the baseline controller to maintain state on the sliding curve.The inner-loop controller is based on backstepping technique to track the AOA command generated by outer-loop controller.Barrier Lyapunov Function(BLF)design is employed to satisfy AOA requirement.Moreover,a novel auxiliary state is introduced to remove the restriction of BLF design on initial tracking errors.Dynamic Surface Control(DSC) is utilized to ease the computation burden.Rigorous stability proof is then given,and AOA is guaranteed to stay in predefined region theoretically.Simulations are conducted to verify the efficiency and superior performance of the proposed method.
1. Introduction
Hypersonic Flight Vehicle (HFV) has long been the focus of world-wide researchers for its huge potentials in both military and civilian fields.1The high lift-to-drag property enables HFV to have large cross range and a cost-effective access to space.2However, cruising over the Mach number of 5 in large flight domain brings many uncertainties in the modelling of HFV.Also, for safety reasons, HFV should satisfy various constraints such as physical constraint on actuator, Angle of Attack (AOA) constraint to avoid inlet unstart, etc. These problems make the design of HFV controller full of challenges.
A necessary condition before regular controller design is the acquisition of mathematical model.Different models for HFV were constructed for cruising and reentry phase. In Ref. 3, a nonlinear longitudinal HFV model was built with piston theory.The implicit expression of aerodynamics prevented it from controller design.Then,in Ref.4,the model was approximated with polynomial curve fittings and the Control-Oriented Model (COM) was obtained. Since then, many studies have been conducted based on COM for it reflects the main characteristics of HFV.
The basic concern for the controller design of HFV is stability. In Ref. 4, integrator enhanced approximate feedback linearization method was proposed to achieve reference tracking.However,it neglects the coupling between lift and elevator and the unstable zero dynamics may render closed-loop system unstable. In Ref. 5, a canard was added to eliminate the side effects of the elevator. The controller was constructed by sequential loop closure with combination of robustness analysis and adaptive technique. Instead of improving control authority, Ref. 6 employed output redefinition to stabilize the internal dynamics. Relevant studies can also be found in Refs. 7,8. Considering the large envelope of HFV, Ref. 9 adopted gain-scheduled switching method to stabilize a flexible HFV which was transformed into a Linear Parameter Varying(LPV) model. For LPV model, Ref. 10 designed an adaptive sliding mode controller to guarantee asymptotical stability with unknown uncertainties. Recently, instead of switching between linearized model, switched COM was used in order to better describe the HFV dynamics in the full envelope.11The controller construction was mainly based on multiple Lyapunov function and neural adaptive control method.12
Many studies were then conducted to gain tracking performance of HFV with various advanced control methods. In Ref. 13, based on system transformation and the construction of performance functions,HFV with non-affine in control feature could achieve desired transient performance.Ref. 14 proposed a non-singular terminal sliding mode controller for a linearized model with transient response analysis. Fractional order PID and active disturbance rejection control were combined in Ref.15 to coordinate the requirements of rapidity and small overshoot.Ref.16 resorted to adaptive fast terminal sliding mode control and a non-homogeneous disturbance observer to achieve finite-time stability of the sliding surface, in presence of input saturation. Other studies based on finitetime stability can be found in Refs. 17,18. Studies on fast altitude control based on finite-time stability theory indeed provide a powerful tool to guarantee that the convergence time of the system is finite.However,it does not mean that the convergence process is necessarily desirable without choosing large control gains. Moreover, as the altitude tracking error decreases,the tracking performance under the static gain strategy declines.
Another essential problem of HFV control is the restriction of AOA. This problem is raised by the utilization of scramjet engine, which demands a suitable condition to work, or else inlet unstart phenomena may happen.19Many researches are conducted regarding this problem and the key technique adopted is the so-called Barrier Lyapunov Function (BLF)method, which can theoretically limit output into prescribed interval and has been adopted to solve output constraint problems.20Refs. 21,22 explored AOA constraint problem by estimating AOA command and restricting its tracking error with BLF method.Then,Ref.23 replaced the tedious estimate process with amplitude limitation of the command,and restriction of AOA was achieved even when actuator faults occur. It should be pointed out that a fundamental requirement of BLF method is that the initial tracking error should lie in the permissible region. Though this problem can be avoided by careful tuning of control gains, it requires extra effort and the accessible range of parameters is limited. Unfortunately,previous studies ignore this problem.
Inspired by the previous discussions,in this paper,we study the control problem of fast altitude tracking for HFV with AOA constraint. From the perspective of physical intuition,as lift is the dominate force of HFV,to improve the maneuverability of the vehicle,large AOA is needed.The requirement of tracking performance and the limited AOA form a contradiction, which makes the design of controller a more challenging problem.We adopt a two-loop structure where outer loop generates AOA command for inner loop tracking. To improve altitude tracking performance, the outer-loop controller is developed in phase plane and involves a Bang-Bang type control law to avoid reduction of the performance as approaching the reference altitude. Though Bang-Bang controller is widely adopted in many control problems24,25to obtain optimal performance,it is not suitable to HFV tracking control problem as trim flight cannot be realized, and we will solve this problem with novel modifications. For inner controller, we employ BLF technique and introduce a novel auxiliary system to relax the requirement on initial tracking error.Moreover, to the best of our knowledge, the combination of Bang-Bang controller and BLF design has not been studied before.
To conclude, this paper focuses on fast altitude tracking control for HFV with AOA restrictions in the presence of uncertain parameter and disturbances.The main contributions of this study can be concluded as follows:
(1) Phase plane design can account for the influence of air density changes over a large altitude range directly.
(2) Bang-Bang controller and FL control law are combined to formulate a smooth trajectory which can be viewed as a special sliding curve from the perspective of sliding mode control. Bang-Bang approach serves as the reaching phase controller, and comprehensive discussions are made to guarantee that any point in the phase plane can reach to the sliding curve and converge to the origin as soon as it stays on the curve.
(3) To maintain states on the sliding curve, FERL is designed to remove the influence of model mismatch caused by model assumption and disturbances. Moreover, the chattering problem is effectively reduced.
(4) BLF technique is adopted to guarantee that AOA constraint is never violated during flight. Specially, an auxiliary state is designed to remove the accompanying restriction of BLF design on initial value.
The remainder is organized as follows: in Section 2, the HFV model is introduced, and the control problem is described. Section 3 presents the whole design process of the controller. Simulation results are given in Section 4 and the paper is concluded in Section 5.
2. HFV model and problem formulation
2.1. Description of HFV model
The Control-Oriented Model(COM)for the longitudinal HFV dynamics can be formulated as4
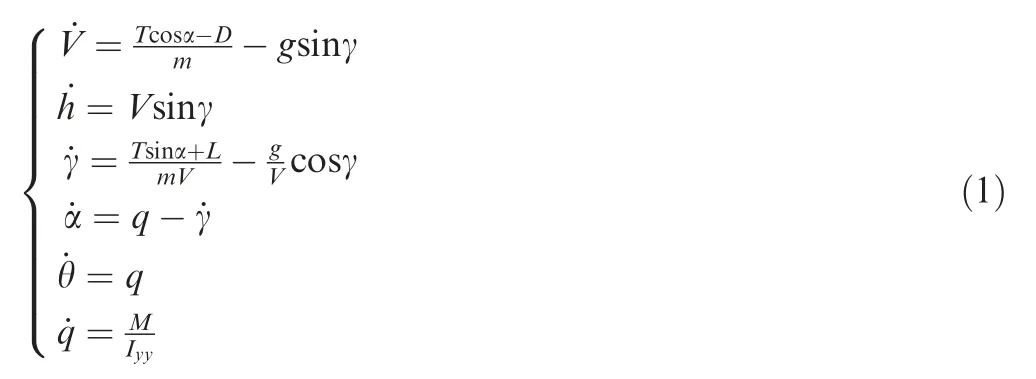
where V is velocity,h is altitude,γ is Flight Path Angle(FPA),α is AOA,θ is Pitch Angel(PA)and q is Pitch Rate(PR).They form the rigid body states of HFV.m is the mass of the vehicle and Iyyis the pitching moment of inertia. The right hand side variables relating to forces include thrust T, drag D, lift L,pitch moment M and gravitational acceleration g. They can be given by
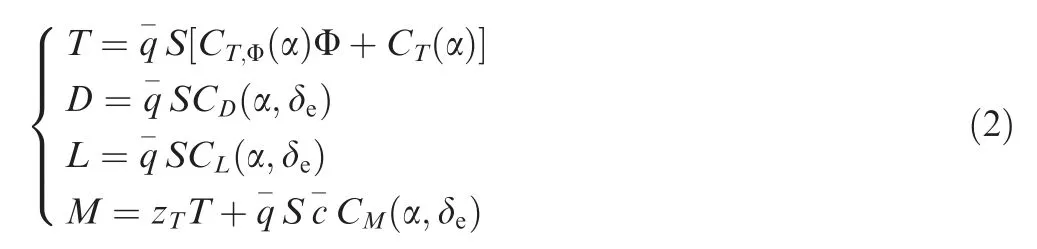
where S, zT, c- and q- stand for reference area, coupling coefficient, mean aerodynamic chord and dynamic pressure respectively. Φ and δeare the two control inputs which are Fuel Equivalent Ratio (FER) and Elevator Angular Deflection(EAD). The rest variables are aerodynamic coefficients which can be further expressed as

2.2. Problem formulation
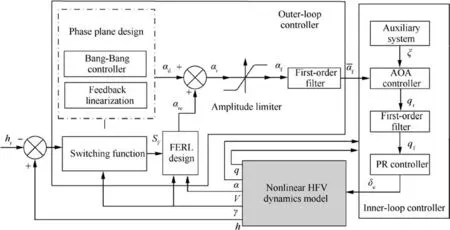
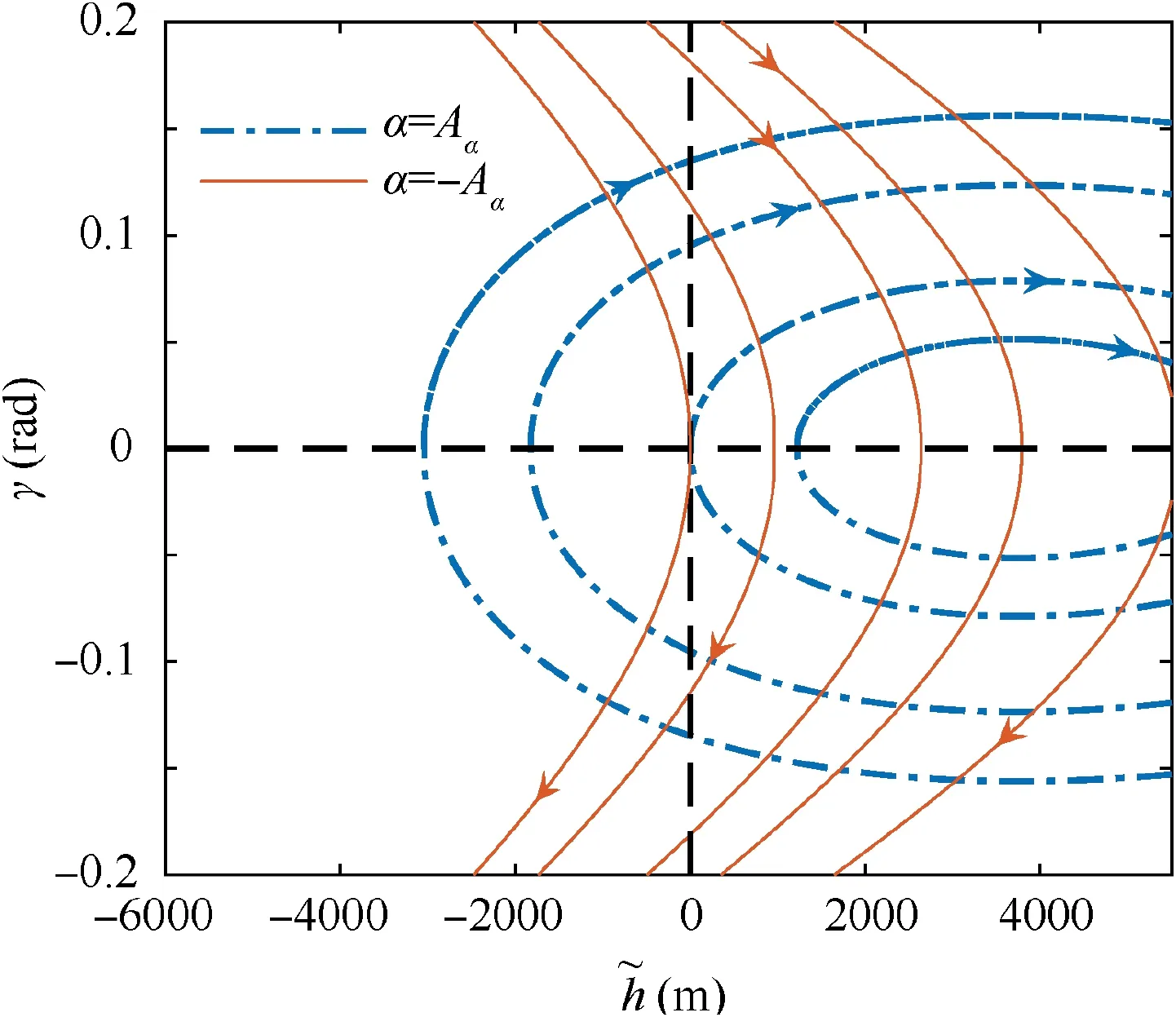
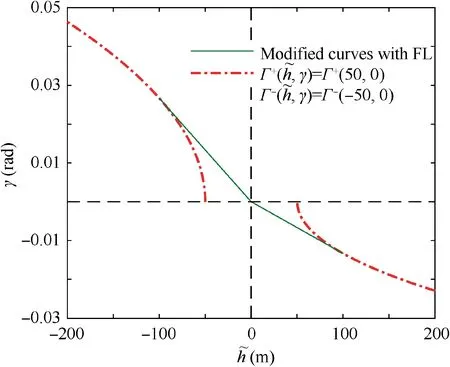
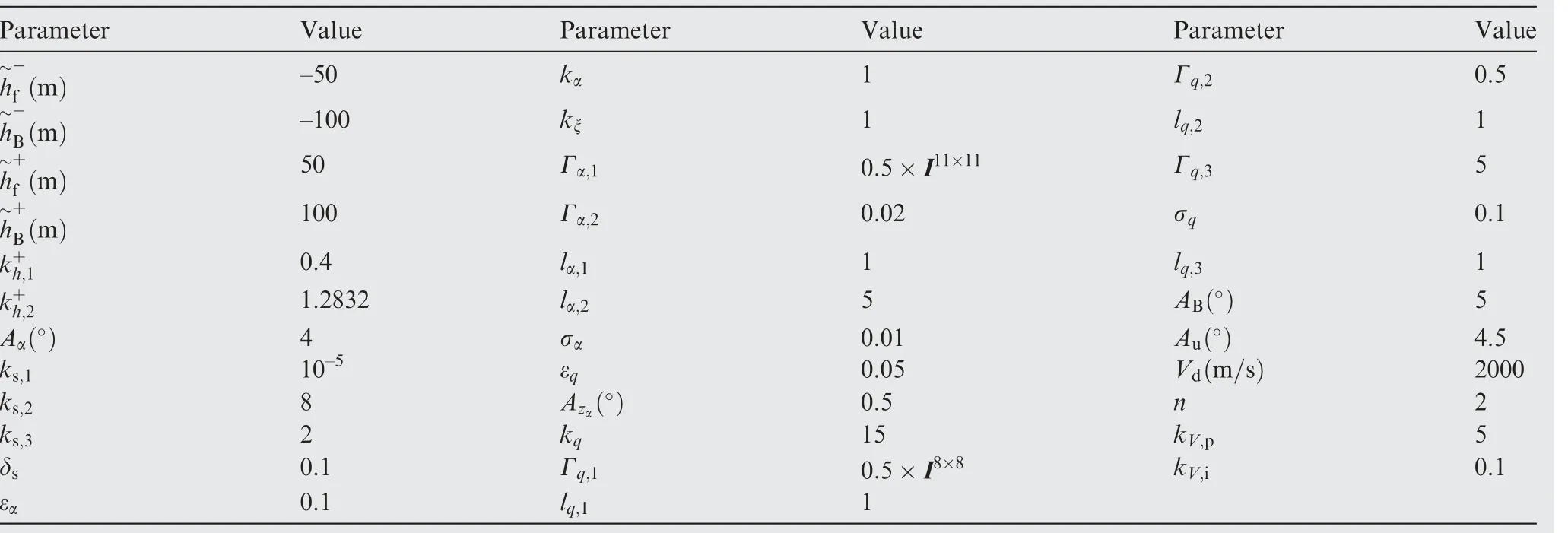
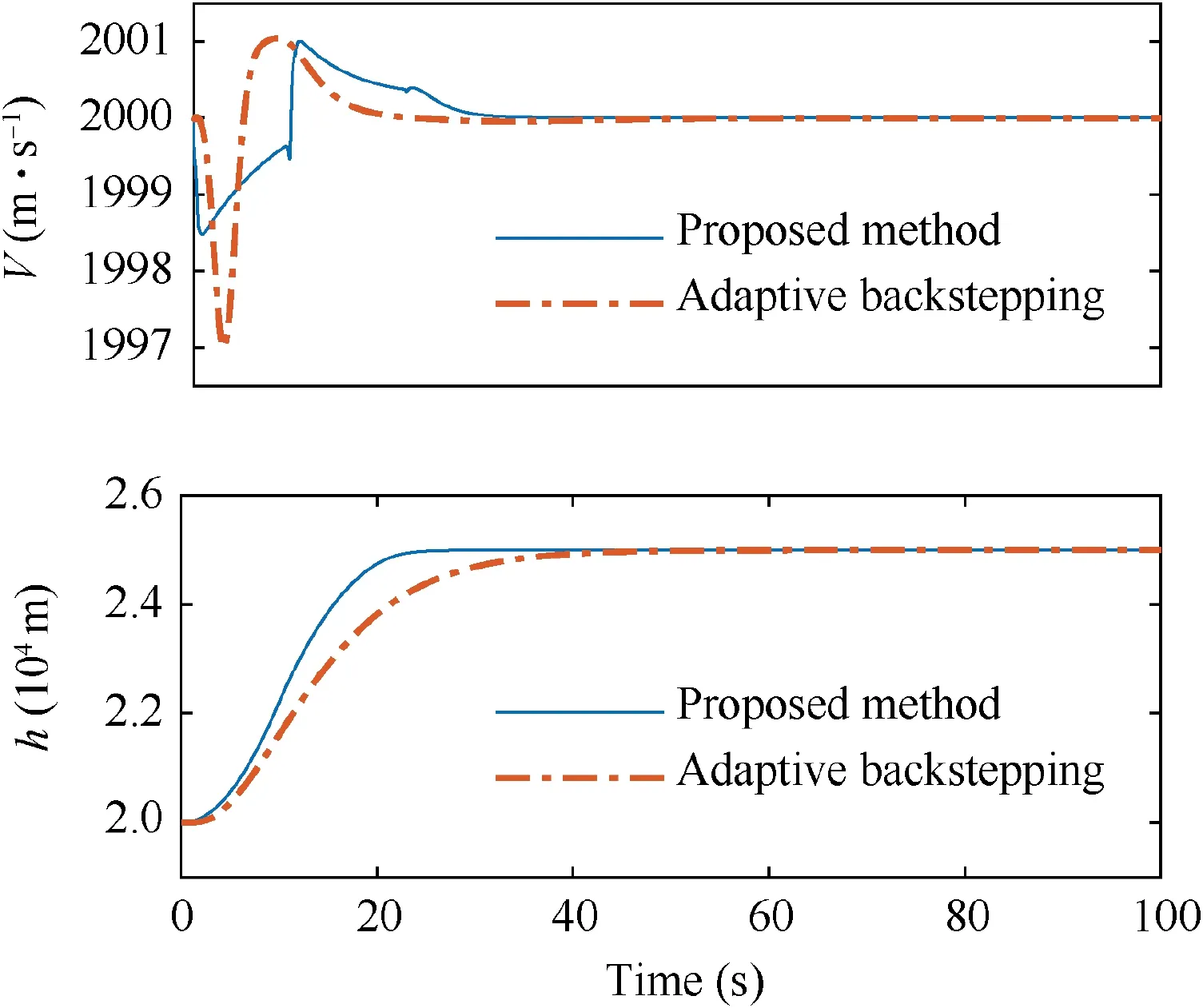
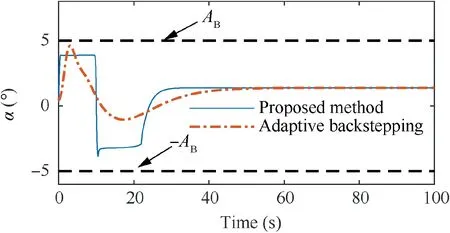
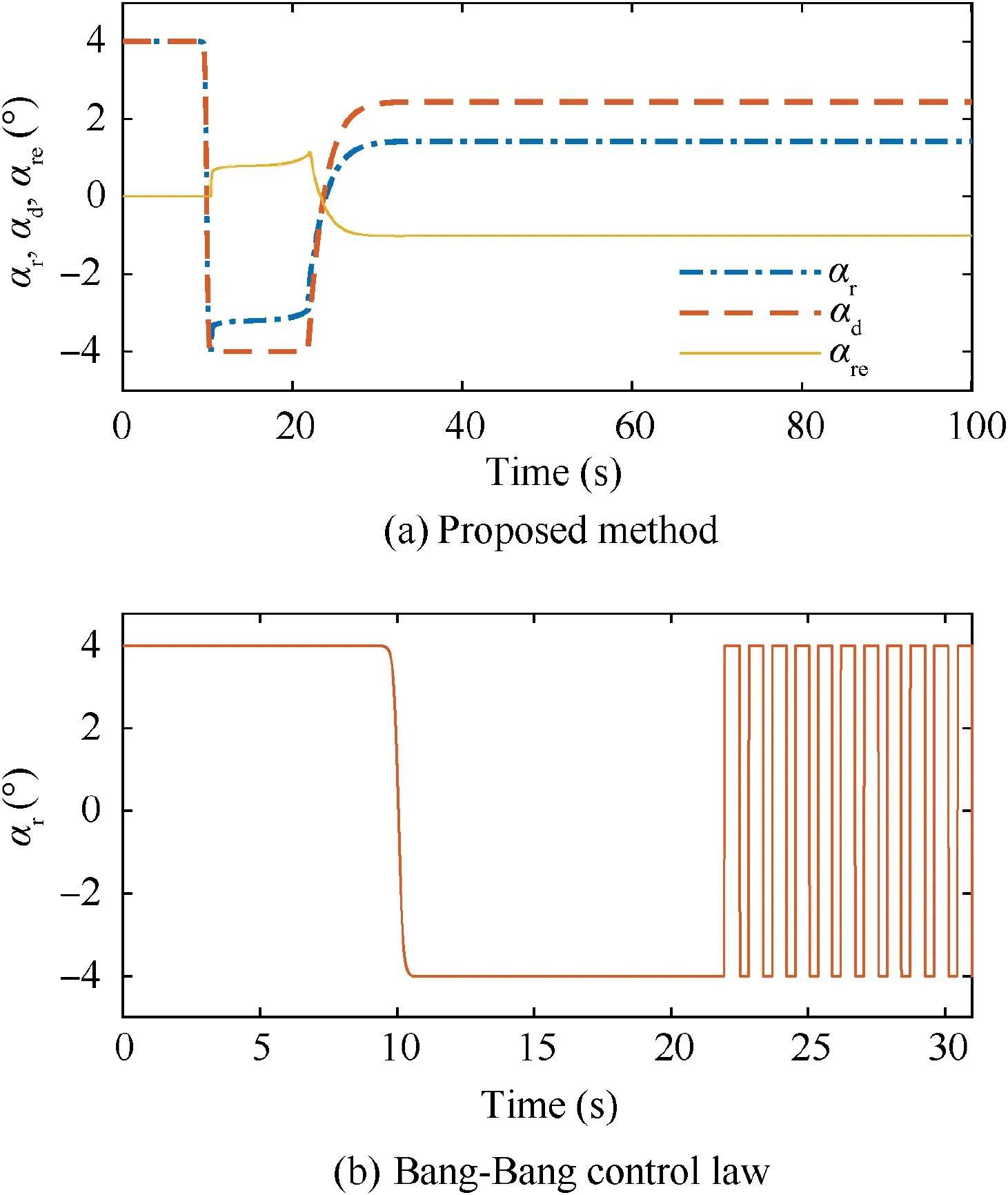
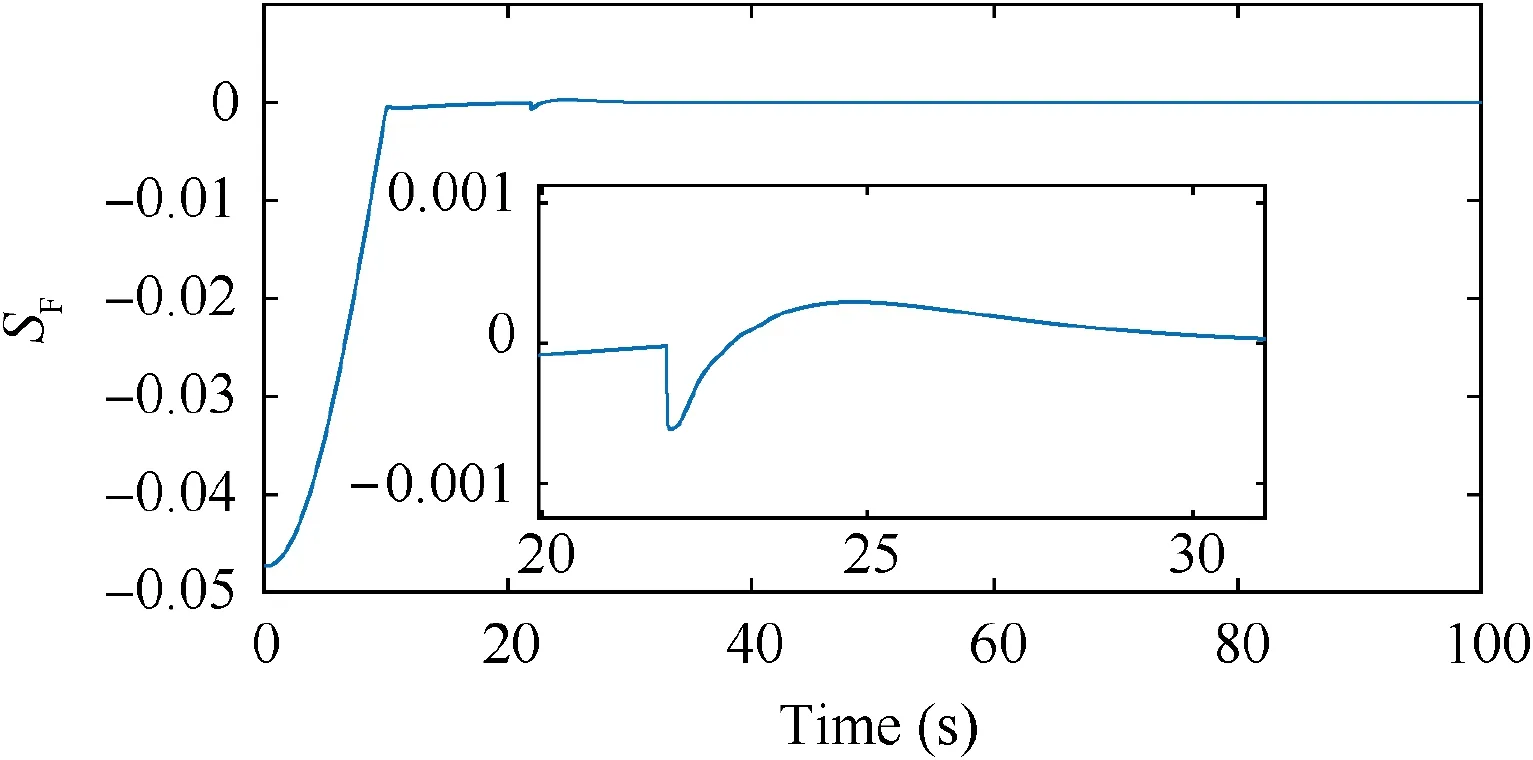
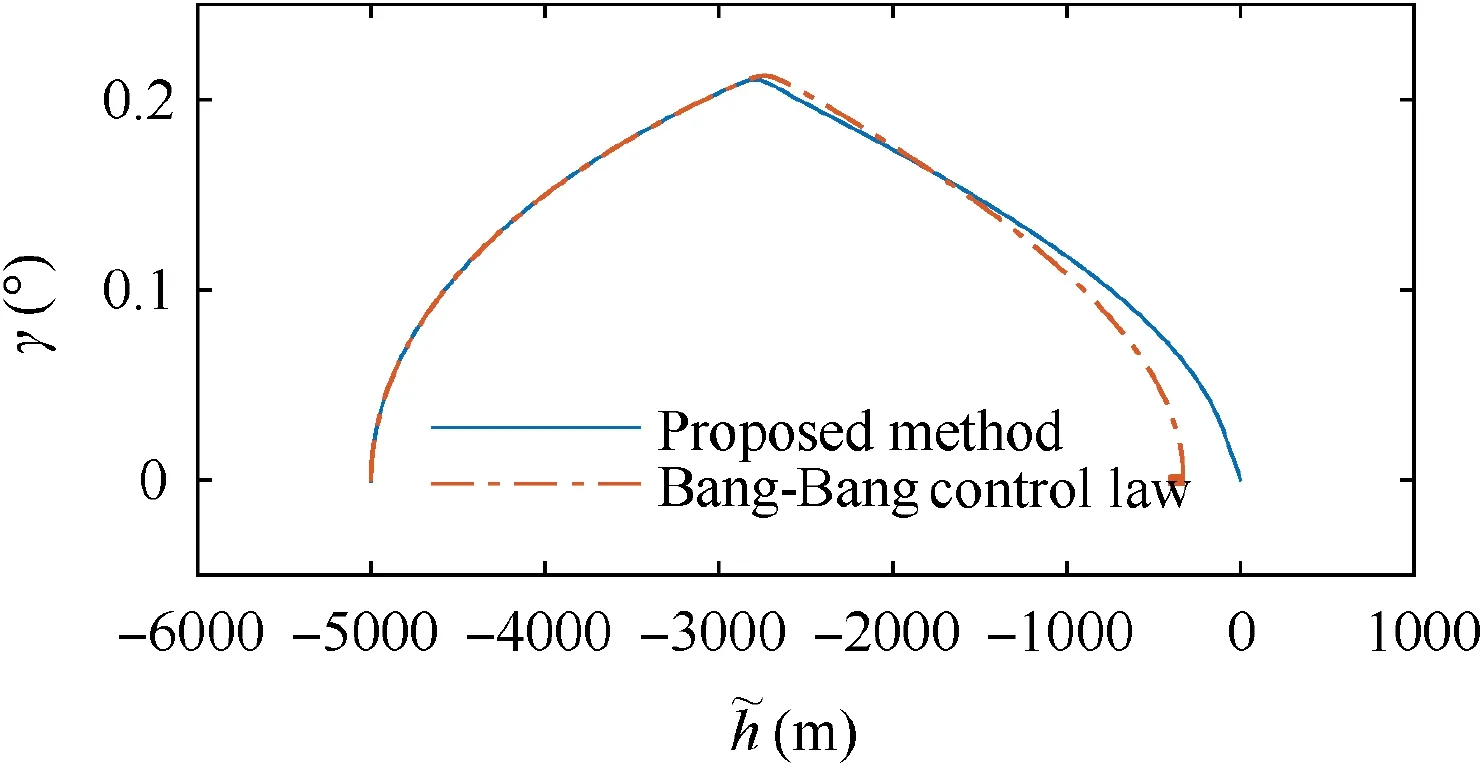
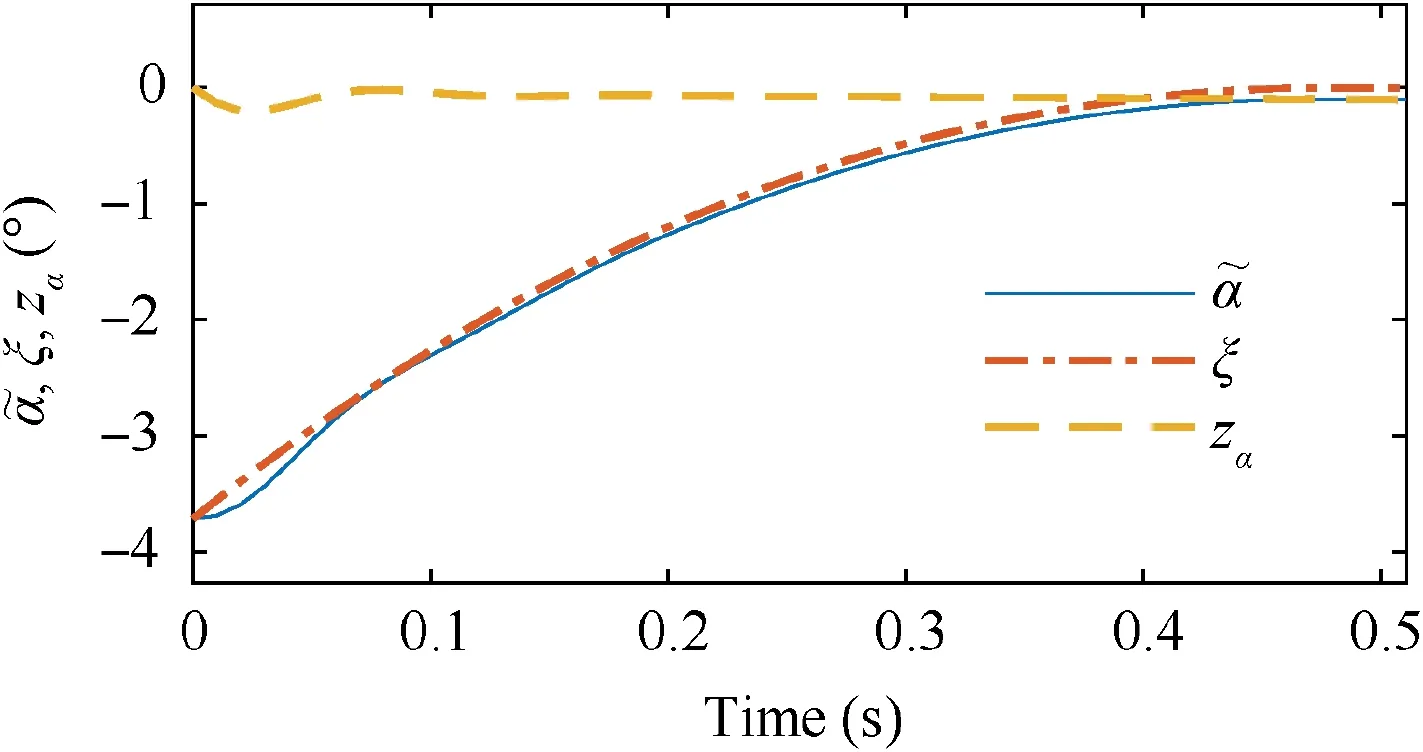
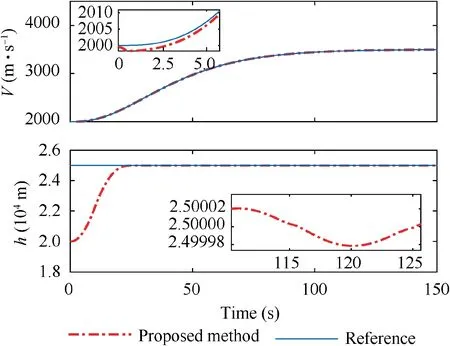
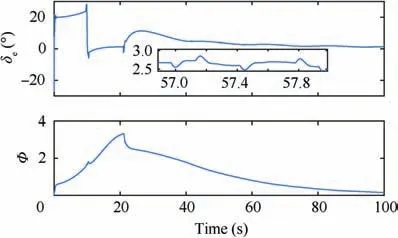
The aim of this paper is to develop an adaptive controller based on phase plane design, to enable fast altitude tracking performance without violation of AOA restriction,in the presence of unknown parameters and bounded disturbances. For setpoint altitude tracking, hrdenotes the reference altitude which is a constant signal. Vrstands for the time-varying reference velocity.During flight,-AB<α In detail,the original model is decoupled into velocity and altitude subsystems which are controlled by FER and EAD separately. The control structure of altitude subsystem is depicted in Fig.1.It can be seen that tracking of hris achieved through a two-loop control structure, that is, the outer loop composed of h and γ dynamics, and inner loop containing α, q and auxiliary state ξ. The outer-loop controller is developed in phase plane accompanied with sliding mode control technique. αd,SF, αre, αr,αfand α-fare the baseline controller, the switching function, the reaching law, the composite controller, the constrained control signal and the filtered control signal, respectively. The inner-loop controller is based on DSC and BLF method, to produce δewhich guarantees precise tracking of. qrand qfare the virtual control signal of AOA channel and the filtered control signal,respectively.The detailed design process will be given in the following sections. 3.1.1. Phase plane design preliminaries Thus, it is plausible to neglect the influence of δγin design process.Further,the design is conducted under a fixed velocity and nominal condition, and thus V=Vdand Δγ=0. Consequently,the differential equation of the phase plane trajectory is simplified as Fig. 1 Structure of altitude controller. Fig. 2 Integral curves families in phase plane under Bang-Bang controller. In this way, any point in the phase plane can reach the switching curves under Bang-Bang controller, and then approach the origin.Remark 1. Eq. (6) is a great substitute of the original Eq. (5)because it reserves the major characteristics of HFV dynamics and is analytically solvable as well. The discrepancies between the design and practical cases are to be compensated with novel techniques which will be introduced later. 3.1.2. Switching curves modification where Fig. 3 Integral curves families in phase plane under Bang-Bang controller. Fig. 4 Switching mechanism of any point in phase plane. 3.1.3. Reaching law design As mentioned in Section 3.1.1, there exists mismatch between design model and actual model. Therefore, for disturbed dynamics (4), the point on the switching curve under the predesigned control law (21), may drift away from the switching curve and result in zig-zag motion because of frequently switching (20). This undesirable behavior is normally attenuated by adding a dead zone to the switching curve.25However,this solution sacrifices the tracking accuracy and toggle switch may still happen. To solve the aforementioned problems, we refer to the reaching law design,27and the baseline controller(21) is augmented with FERL which is denoted by αre. Then,the composite controller is expressed as Taking the time derivative of SFalong the disturbed dynamics (4) gives Remark 5. By choosing appropriately large control parameters satisfying ks,1>δsDγand ks,3>1, system stability can be guaranteed theoretically. Remark 6. The discrepancy between V and Vdis compensated with FERL, to achieve ideal tracking performance and accuracy. However, the more the discrepancy is, the more control effort is needed. Thus, in principle, Vdshould be chosen to minimize the amplitude of V-Vdduring climbing maneuver.However, in practice, compared with the rapid changing altitude,the variation rate of V is rather slow and the range is narrow. A simple but effective strategy is to choose the initial velocity of HFV as Vd,which is adopted in the simulation case. In this subsection,the controller for inner loop containing α and q dynamics is designed based on DSC to track the outer-loop command signal αf. The original equations of the inner-loop dynamics are rewritten into linearly parameterized form 17. Daybreak: In the time before strong artificial light, the work day for the lower classes would begin at dawn with daytime s free, natural light. An early start also allows the parents to lose the children deeper into the woods before they find their own way home.Return to place in story. Noting that ˙qris a continuous function on its domain, it is reasonable to assume that ˙qr| | where kq>0 is a design constant.The update laws for the estimate parameters ^ϑq, ^ψqand ^Dqare constructed as A simple PID type controller accompanied with dynamic inversion strategy forms the velocity controller, to complete the longitudinal controller design of HFV. From Eq. (1), the tracking error derivative is presented as The stability of the velocity subsystem can be ensured by selecting proper gains for kV,pand kV,i. In this section, simulation results under the given controller and other comparative methods including adaptive backstepping and Bang-Bang controllers are presented to demonstrate the effectiveness and the superior performance of the proposed method. HFV is at trimmed cruise and the initial conditions are h=25000 m and V = 2000 m·s-1. Table 1 displays all the control parameter values for simulation. First, consider the case where reference signals are hr=25000 m and Vr=2000 m·s-1.All the uncertain parameters are biased randomly within 20%of their nominal values.Simulation results are presented in Figs. 5–12. Figs. 5 and 6 give the altitude tracking curve and the constrained AOA curve respectively. As depicted in Fig. 5, the proposed method provides much faster climbing performance than adaptive backstepping controller. In view of Fig. 6, it can be found that the AOA can be strictly limited within the predefined bound -5°,5°[ ]. For adaptive backstepping method, the control parameters are adjusted carefully to meet AOA restriction and acquire good performance simultaneously. For the proposed method, the trial and error process is reduced and better tracking performance can be achieved. Then we show the effectiveness of the proposed outer-loop controller by comparison with a Bang-Bang controller. Fig. 7(a)shows that αrconverges to equilibrium value owe to the utilization of FL control law.In comparison,according to Fig.7(b), Bang-Bang control generates zig-zag AOA command,which is undesirable as the inner controller can hardly track the signal well, and results in large tracking errors. Fig. 8 depicts the curve of SF. It can be seen that SFis sufficiently close to zero regardless of mismatch of model caused by modelreduction and parameter variation. Therefore, the tracking accuracy of altitude is guaranteed. The sudden change of SFat around 22 s is induced by the discontinuity of the piecewise function at the border point=-100 m.From Fig.9,system states in both two simulations start at the point of(-5000 m,0 rad). Under the proposed method, the state converges to the origin point (-0 m,0 rad) precisely. However,the state under Bang-Bang control law fails to arrive at the origin and keeps oscillating around the point of (-200 m,0 rad). Table 1 Control parameters. Fig. 5 Tracking performance. Fig. 6 AOA response. Fig. 7 AOA command under both two controllers. Fig. 8 Switching function value. Fig. 9 Phase plane trajectories. Fig.10 AOA tracking error α~,auxiliary state ξ and compensated error zα. Fig. 11 Elevator deflection angle δe. Fig. 12 Altitude and velocity tracking. Fig. 13 AOA response. Fig. 14 Estimation of Dα and Dq. Fig. 15 Elevator deflection and fuel equivalent ratio. Fig.13 shows that the proposed controller can satisfy AOA constraint.Chattering is effectively reduced and the small amplitude oscillation is induced by external disturbances. Fig. 14 depicts the time-history of the two disturbance estimates.Fig.15 shows the control inputs δeand Φ.The simulation results of the second case indicate that, though the proposed method is designed under fixed velocity and nominal parameters,it is still effective in the situation with variation of velocity and parameters as well as time-varying external disturbances. (1) A two-loop control structure is built to solve the fast altitude tracking problem of HFV. For outer-loop controller,state trajectories are analyzed in phase plane with direct consideration of air density change. Then sliding curve is developed with combination of Bang-Bang control law and FL controller.FERL is augmented with the baseline controller to tackle uncertainties and disturbances. Under the proposed composite control law,HFV state could be arbitrary close to the sliding curve and meanwhile the problem of chattering is effectively reduced. (2) The inner-loop controller guarantees that the tracking error of AOA command is arbitrary small with the combination of adaptive backstepping and BLF design.Owing to the novel finite-time stable auxiliary state,the initial constraint of BLF design is relaxed. Moreover, AOA could be strictly limited within the predefined intervals during rapid maneuver. (3) The complexity of the proposed control law is greatly reduced compared with traditional backstepping based control techniques, as the repeated differentiations of virtual controls are eliminated with synthesis of phase plane design and DSC method. (4) Comparative simulations verify the superior altitude performance of the proposed method and its high robustness to the uncertainties and disturbances. Acknowledgements This study was supported by the National Natural Science Foundation of China (Nos. 61833016, 61873295, 61622308 and 61933010).3. Fast tracking controller design
3.1. Outer-loop controller design











3.2. Inner-loop controller design
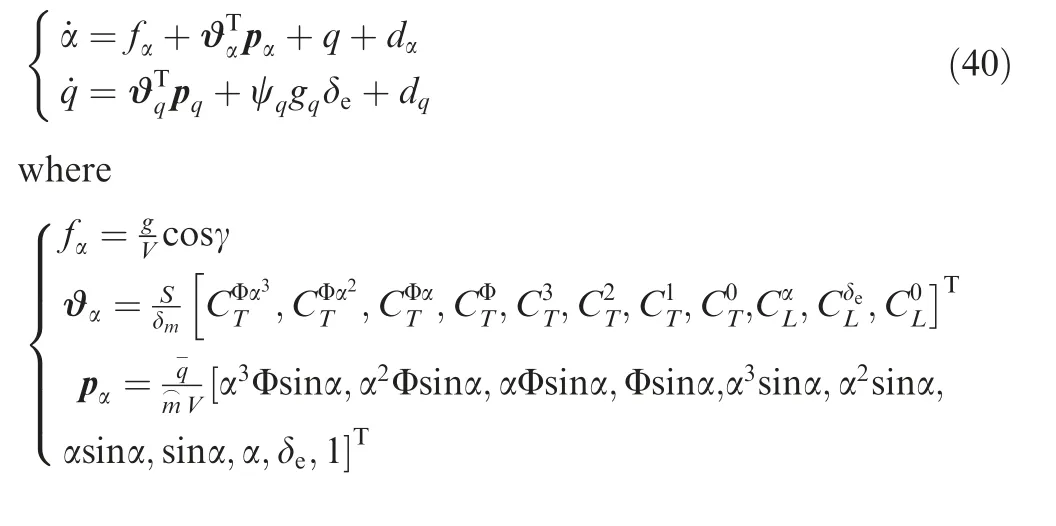


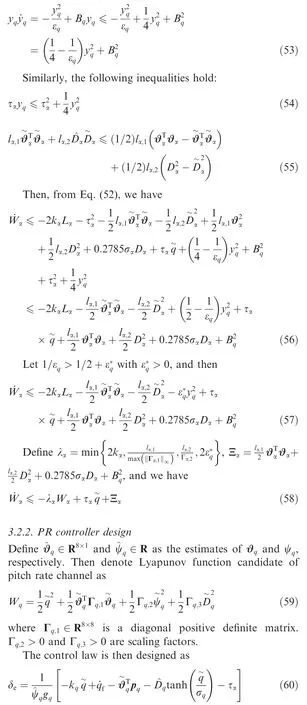



3.3. Velocity controller design

4. Simulations





5. Conclusions
 CHINESE JOURNAL OF AERONAUTICS2021年2期
CHINESE JOURNAL OF AERONAUTICS2021年2期
