Advanced high-order nonlinear chirp scaling algorithm for high-resolution wide-swath spaceborne SAR

Zhirong MEN, Pengo WANG,*, Jie CHEN, Chunsheng LI, Wei LIU,Wei YANG

a School of Electronic and Information Engineering, Beihang University, Beijing 100083, China

b Electronic and Electronic Engineering Department, University of Sheffield, Sheffield S1 3JD, UK

KEYWORDS High-Resolution Wide-Swath (HRWS);Imaging method;Second-Order Equivalent Squint Range Model(SOESRM);Signal processing;Synthetic Aperture Radar(SAR)

Abstract Spaceborne Synthetic Aperture Radar(SAR)is a well-established and powerful imaging technology that can provide high-resolution images of the Earth’s surface on a global scale. For future SAR systems, one of the key capabilities is to acquire images with both high-resolution and wide-swath.In parallel to the evolution of SAR sensors,more precise range models,and effective imaging algorithms are required. Due to the significant azimuth-variance of the echo signal in High-Resolution Wide-Swath(HRWS)SAR,two challenges have been faced in conventional imaging algorithms.The first challenge is constructing a precise range model of the whole scene and the second one is to develop an effective imaging algorithm since existing ones fail to process highresolution and wide azimuth swath SAR data effectively. In this paper, an Advanced High-order Nonlinear Chirp Scaling (A-HNLCS) algorithm for HRWS SAR is proposed. First, a novel Second-Order Equivalent Squint Range Model (SOESRM) is developed to describe the range history of the whole scene, by introducing a quadratic curve to fit the deviation of the azimuth FM rate. Second, a corresponding algorithm is derived, where the azimuth-variance of the echo signal is solved by azimuth equalizing processing and accurate focusing is achieved through a high-order nonlinear chirp scaling algorithm. As a result, the whole scene can be accurately focused through one single imaging processing. Simulations are provided to validate the proposed range model and imaging algorithm.

1. Introduction

Spaceborne Synthetic Aperture Radar (SAR) is a wellestablished remote sensing technology, capable of acquiring images of Earth’s surface independent of weather conditions and sunlight illumination. With beam steering techniques,the sliding spotlight mode has been employed to support highresolution applications.Since the first spaceborne SAR,Seasat was launched in 1978,1,2significant progress has been made in this area. With the launch of the SAR satellites Radarsat-2,TerraSAR-X, TanDEM-X, COSMO SkyMed, ALOS-2 and COSMO SkyMed Second Generation (CSG), the resolution of spaceborne SAR has been upgraded from tens of meters to the sub-meter level,and the ratio of imaging area to resolution element has been increased from 50 million to 252 million.2–9Benefiting from an advanced SAR sensor technology,the TerraSAR-X Next Generation(TSX-NG)will allow a high spatial resolution down to 0.25 m and a 5 km swath in both azimuth and range directions.10,11For TSX-NG, the ratio of imaging area to resolution element will increase to 400 million.In the future,spaceborne SAR systems are expected to acquire much wider areas with high-resolution for numerous applications. Suppose the swath of High-Resolution Wide-Swath(HRWS) SAR can be enlarged to 20 km (Azimuth)×20 km(Range) with the same resolution of TSX-NG, the ratio of image area to resolution element would reach 6.4 billion,much higher than the magnitude of current SAR systems. Studies have demonstrated that through a longer integration time, a larger squint angle and adopting the Continuously Varying Pulse Repetition Frequency(CVPRF)strategy,the echo signal can be effectively acquired.12However, the much longer integration time and larger squint angle in azimuth would pose many challenges for spaceborne SAR signal processing,particularly the imaging part.

Among them is how to construct a precise range model to describe the range history more accurately in the HRWS case.Many studies have been performed in this area, with various accurate range models put forward. The most well-known range model in spaceborne SAR is the Hyperbolic Range Equation Model (HREM) or the Equivalent Squint Range Model (ESRM),13,14which is derived from the straight track and is adapted to the curved orbit of spaceborne SAR by equivalent velocity and squint angle. Based on either HREM or ESRM, several variations have been proposed and applied in the classic imaging algorithms. A Fourth-order Doppler Range Model (DRM4) was proposed for high-resolution spaceborne SAR, where the range model perfectly compensates the actual range history up to the quartic term.15An Advanced Hyperbolic Range Equation (AHRE) was introduced for Medium Earth Orbit (MEO) SAR, where an additional linear term is introduced into the conventional HREM to handle the focusing issue of an azimuth resolution around 3 m with altitude ranging from 1000 to 10000 km.16A Modified Equivalent Squint Range Model (MESRM) was developed for high-resolution spaceborne SAR, where an additional cubic component and quartic component are introduced into the conventional ESRM, and a better imaging result can be obtained.17Recently,range model for curvilinear trajectory airborne SAR, which involves three-dimensional velocity and acceleration is proposed. Based on Chebyshev approximation, the range model in the form of equivalent hyperbolic equation is obtained and shows high precise for a target point within its synthetic aperture time.18

However, all these studies are focused on the range model of a single point target, without considering the influence of azimuth-variance on the whole scene. As a result, the ground scenes in their simulations were both chosen as 4 km in azimuth by Luo15and Wang17et al, when the resolution is set between 0.25–0.30 m. Once the azimuth swath is enlarged to 20 km, the targets at the azimuth edge will suffer from severe degradation due to the mismatch between the range model and the Doppler parameter, which varies significantly along with different targets in the azimuth direction. To describe the azimuth-variance of the Doppler parameter, a Second-Order ESRM (SOESRM) is proposed in this paper, where a quadratic curve is introduced to fit the deviation of azimuth FM rate, so that a more accurate description of range history can be obtained.

Regarding the focusing algorithm for spaceborne SAR,the Chirp Scaling Algorithm(CSA)is commonly employed due to its good phase preservation and high-efficiency properties.19To improve the performance, some modified CSAs have been proposed,such as the Advanced Non-Linear Chirp Scaling(ANLCS) algorithm,16the Higher-order Hybrid Correlation Algorithm (HHCA)17and the High-order NonLinear Chirp Scaling (HNLCS) algorithm.20However, all these algorithms are focused on compensating for the spatial variant crosscoupling phase between range and azimuth, without considering the azimuth-variance of the Doppler parameters. As a result, they cannot be applied to HRWS spaceborne SAR directly.

In this work, an Advanced High-order Nonlinear Chirp Scaling (A-HNLCS) algorithm is proposed, where the azimuth-variance of the Doppler parameters is removed by equalization filtering,and accurate focusing is realized through the higher-order nonlinear chirp scaling algorithm. The residual azimuth-variance,image aliasing,and geometric distortion are removed by a modified resampling process.Simulations are performed to show significantly improved imaging results.

It is necessary to point out that researchers of the German Aerospace Center (DLR) have also proposed a concept of HRWS mode which aims to achieve a high resolution (meter level)in azimuth direction and a wide swath(hundreds of kilometers) in range direction.21,22However, there are mainly two differences between the HRWS mode of DLR and the concept discussed in this paper. Firstly, DLR aims to operate in a 2 m azimuth resolution with a 400 km range swath using both Digital Beam-Forming (DBF) and multi-channel techniques to extend the capability of SAR systems,21but in this paper, we emphasize a much higher azimuth resolution (0.25 m) with 20 km swath in azimuth by increasing the squint angle of SAR. Secondly, challenges faced in signal processing for the two concepts are different. For the HRWS mode of DLR,the main challenge is the processing of the loss of pulses caused by blockage over a large range swath.22Meanwhile,due to the 2 m azimuth resolution, the ERSM and CSA are precise enough for signal processing. In this paper, azimuth variance becomes the main challenge for 0.25 m azimuth resolution and 20 km swath in both azimuth and range directions,hence,a more precise range model and a more effective imaging algorithm are required.Generally,the concept of DLR emphasizes the coverage to observe large-scope areas, but the concept in this paper focuses on the observation of high-value targets with a very high resolution and wide swath.

This paper is organized as follows: Based on azimuthvariance analysis of the range history, a second-order ERSM is proposed in Section 2.The corresponding advanced imaging algorithm for HRWS spaceborne SAR is developed in Section 3. Simulation results are provided in Section 4, and conclusions are drawn in Section 5.

2. Modified range model

An accurate range model is the basis of SAR signal processing,which describes not only the range history of point targets but also the variation of Doppler parameters. The spaceborne SAR geometry in Earth-centered rotating coordinates is illustrated in Fig. 1, where the actual path is represented by the black solid line,and the paths based on HREM and MESRM are denoted by the blue dotted line and red dashed line,respectively. T1and T3represent the edge points of the scene in the azimuth direction, and T2presents the center point. Siand Ei,where i={1, 2,3},are the start and end positions of the illumination for the corresponding target Ti. It can be seen that MESRM can match the range history of T2, but not precise enough for the points which are far away from the azimuth center, i.e., T1and T3. R0is the slant range at Doppler center time of T2.

By introducing an additional cubic component and quartic component into the conventional ESRM, MESRM is given as20

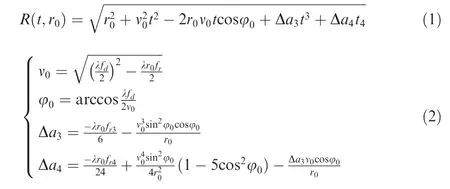
where t is the azimuth time, r0is the slant range at Doppler center time,ν0is the equivalent radar velocity between the scatter and the SAR,φ0is the equivalent squint angle,Δa3and Δa4represent cubic and quartic coefficients, λ is the signal wavelength, and fd, fr, fr3and fr4denote the Doppler centroid frequency, the azimuth Frequency Modulation (FM) rate, the rate of the azimuth FM rate and the second-order derivative of the azimuth FM rate, respectively.

Differentiating Eq.(1)with respect to t for the point with a distance of x0from the scene center, we have

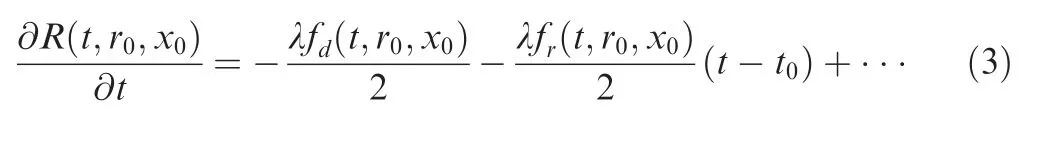
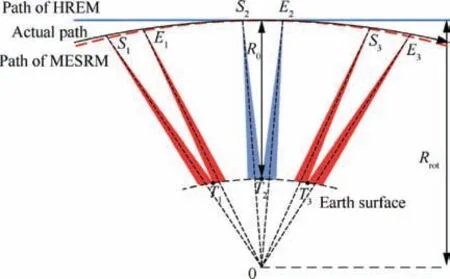
Fig.1 Geometry of sliding spotlight mode for spaceborne SAR.

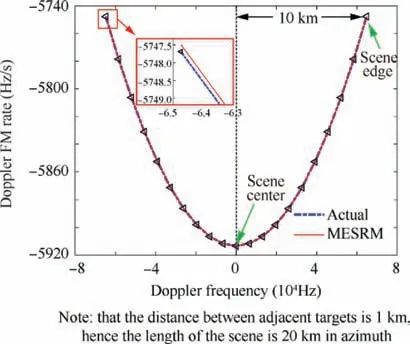
Fig. 2 Mapping relationship between fd and fr for 21 point targets in azimuth.

Table 1 List of simulation parameters.

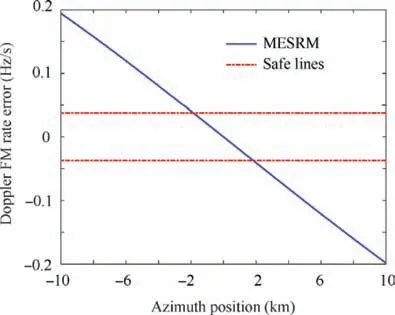
Fig.3 Doppler FM rate error as a function of azimuth position caused by MESRM.

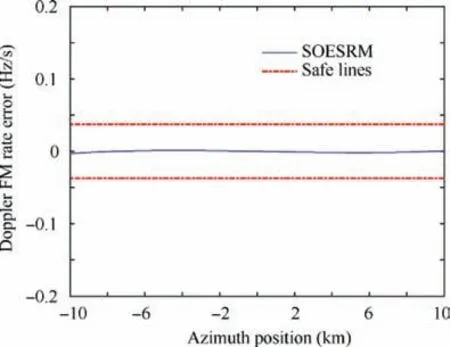
Fig.4 Error of Doppler FM rate for different azimuth positions using SOERSM.

Orbit error(velocity error and position error of SAR satellite) would introduce error to the estimates of parameters of range models such as Doppler frequency, Doppler FM frequency, etc. Also, this is a challenge for all range models and SAR systems are equipped to offer accurate orbit measurements.The absolute 3-D orbit accuracy of TerraSAR-X is better than 10 cm,23and the 3-D orbit and velocity accuracy of Gaofen-3 is better than 5 cm and 0.05 mm/s,24respectively.Analysis of Doppler FM rate error caused by SOESRM and MESRM with velocity error fixed as 0.05 mm/s and position error fixed as 10 cm is given in Fig. 5. It can be seen that the error of the Doppler FM rate is still within the safe lines based on current orbit and velocity accuracy,which means that wellfocused images can be achieved by the range model of SOESRM.

To compare the difference between MESRM and the proposed SOERSM, we expand the range model of Eq. (7) based on Taylor polynomial as Eq.(9)(see Appendix A).Also,Chebyshev orthogonal decomposition is another strategy for the expansion of the range model.18

Fig.5 Doppler FM rate error caused by SOESRM and MESRM with velocity error fixed as 0.05 mm/s or position error fixed as 10 cm of satellite.

In general, the premise of the expansion in Eq. (9) is to guarantee the phase error is within π/4. Hence, it is necessary to analyse the feasibility of the expansion. To show the accuracy of the expansion of SOERSM, the phase error as a function of illumination time is given in Fig.6,using the orbit and radar parameters listed in Table 1.Lines with different colours represent the phase error of different targets in azimuth.There are 21 targets and the distance between adjacent points is 1 km. It can be seen that the maximum value of phase error is still within π/4, which means that the expansion is effective and would not cause severe degradation to signal processing.

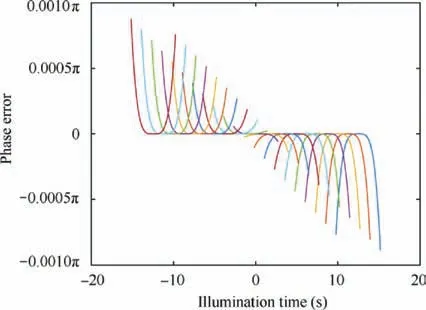
Fig. 6 Phase error as a function of illumination time caused by approximation of SOESRM.

3. Proposed imaging algorithm

3.1. Azimuth preprocessing

where the first exponential term is used to remove the azimuthvariance of the echo signal, and the second one is used to reduce the effect of the transmitted bandwidth; rrefdenotes the reference slant range; fprfrepresents the Pulse Repetition Frequency (PRF); fcrepresents the carrier frequency; Nsubis the azimuth sample number of the sub-aperture;Tsubis the size of the sub-aperture; fd，kis the Doppler centroid frequency of the kth sub-aperture; tkis the center time of the kth subaperture, and ·is the rounding operation.

After azimuth equalizing filter processing,sub-aperture azimuth FFT, delay phase compensation and sub-aperture recombination are performed for azimuth sub-aperture processing,and the 2-D signal spectrum data are obtained in a discrete form without aliasing in the azimuth direction.The delay phase function H2can be expressed as follows:

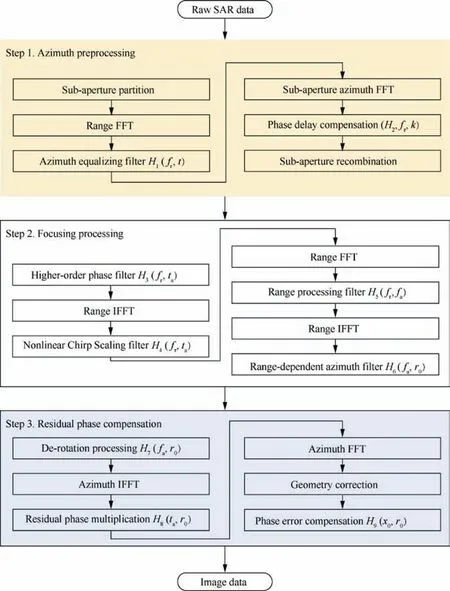
Fig. 7 Block diagram of proposed advanced high-order nonlinear chirp scaling algorithm.

where σ0represents the scattering coefficient,t0is the Doppler center time,τ represents the fast time,c is the speed of light,Kris the range chirp rate,ωrand ωadenote antenna pattern functions in the range and azimuth directions, respectively. x0is the azimuth position of the target.

Using the principle of stationary phase and Fourier transformation, the 2-D Point Target Spectrum (PTS) of Eq. (15)can be obtained as (see Appendix B)

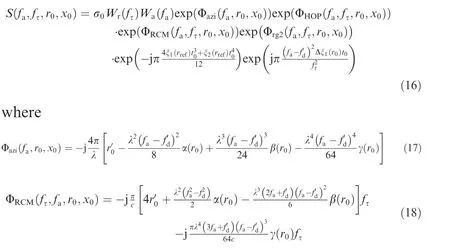
where rrefis the reference slant range. The corresponding parameters are νref, φref, Δa3，refand Δa4，ref.

Substituting Eq.(21)into Eq.(16),the 2-D signal spectrum can be obtained, and the corresponding imaging algorithm is provided in the following section.

3.2. Focusing processing

Since the aliasing effect in the azimuth frequency domain is removed after the improved azimuth sub-aperture processing,the improved higher-order nonlinear chirp scaling algorithm can be employed to implement Range Cell Migration Correction (RCMC), range compression, Second Range Compression (SRC), as well as azimuth compression.

The algorithm starts with higher-order phase compensation and cubic phase filtering in the 2-D frequency domain, as follows

From Eq.(30),it can be seen that the RCMC and SRC are independent of range r0,and the bulk RCMC and SRC can be performed accurately and effectively across the range swath.Accordingly, the range processing filter H5is given by

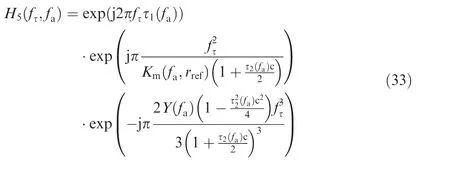
With range IFFT, the data is transformed back to the range-Doppler domain, and then range-dependent azimuthmatched filtering and residual phase compensation can be performed by the azimuth processing filter H6

3.3. Residual phase compensation

Since the target is focused by the higher-order nonlinear chirp scaling algorithm, image aliasing, residual azimuth-variance and realize geometric correction still exist. An azimuth resampling operation is applied to remove the existing residual phase.

The operation begins with de-rotation processing, and the de-rotation phase function H7is given by

4. Simulations and analysis

To demonstrate the performance of the proposed imaging algorithm, raw data is first generated for point targets using the parameters given in Table 1 and the scene shown in Fig. 8. The distances of different targets along the range and azimuth directions are 10.0 km and 1.0 km,respectively.Rectangular weighting is used for both azimuth and range processing.For SAR signal processing,range model is the foundation of an imaging algorithm. In Ref.20, the accuracy of ESRM,DRM4, and MESRM has been compared (see Figs. 4 and 5 in Ref.20), and also focused results using NCS, ωkA and HHCA indicate that HHCA can achieve the best imaging quality when processing SAR data with a high resolution of 0.25 m (see Figs. 13 to 15 in Ref.20). Hence, HHCA is employed for the comparison with the proposed A-HNLCS algorithm.

Fig. 9 shows the Impulse Response Width (IRW) (normalized to the theoretical) curve to azimuth displacement, and Fig. 10 shows the Peak Sidelobe Ratio (PSLR) results to azimuth displacement. In the HHCA, the imaging performance degrades with azimuth displacement. Only targets near the scene center can be focused accurately, and the targets at the azimuth edge suffer from severe degradation. In the proposed A-HNLCS algorithm, all targets of the whole scene can be focused well. The deterioration of the IRW and PSLR is less than 0.5% and 3 %, respectively.

To quantify the focusing performance, the point target analysis results are listed in Table 2, where the ideal PSLR is-13.26 dB, using the rectangular window. The theoretical resolution is calculated according to the following equation:

Fig. 11 shows the azimuth profile of PT1 and PT63, where the red dashed line represents the focused results by HHCA,and the blue solid line represents the focused results by the proposed A-HNLCS algorithm. It can be seen that the edge targets based on HHCA suffer from severe degradation, and significant azimuth main lobe broadening and sidelobe arising can be observed.Compared to the HHCA results,the focusing performance of the proposed algorithm has been improved significantly, and all of the targets are well focused by the proposed method. All these indicate that our proposed focusing algorithm can meet the imaging requirement of highresolution wide-swath spaceborne SAR effectively.

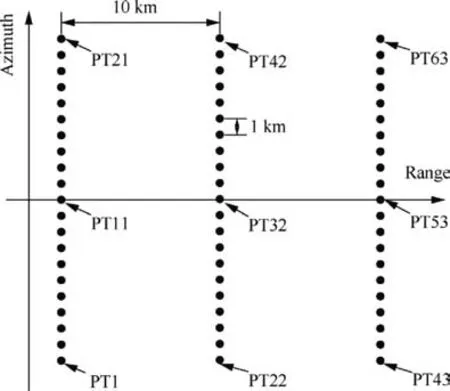
Fig. 8 Ground scene layout in our simulation.

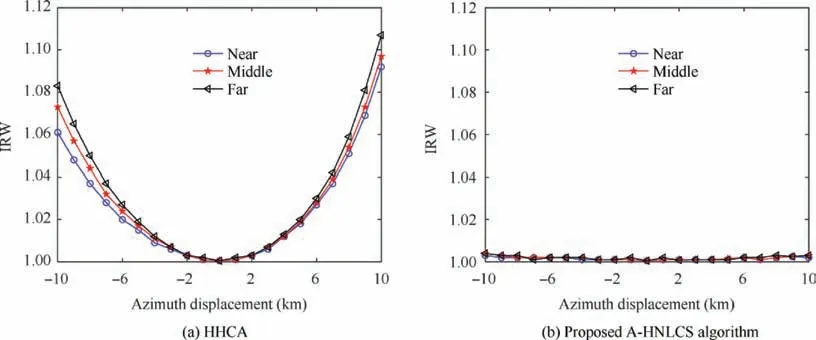
Fig. 9 IRW of the focused result.

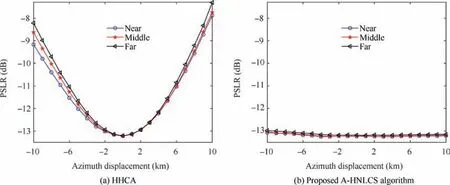
Fig. 10 PSLR of the focused result.

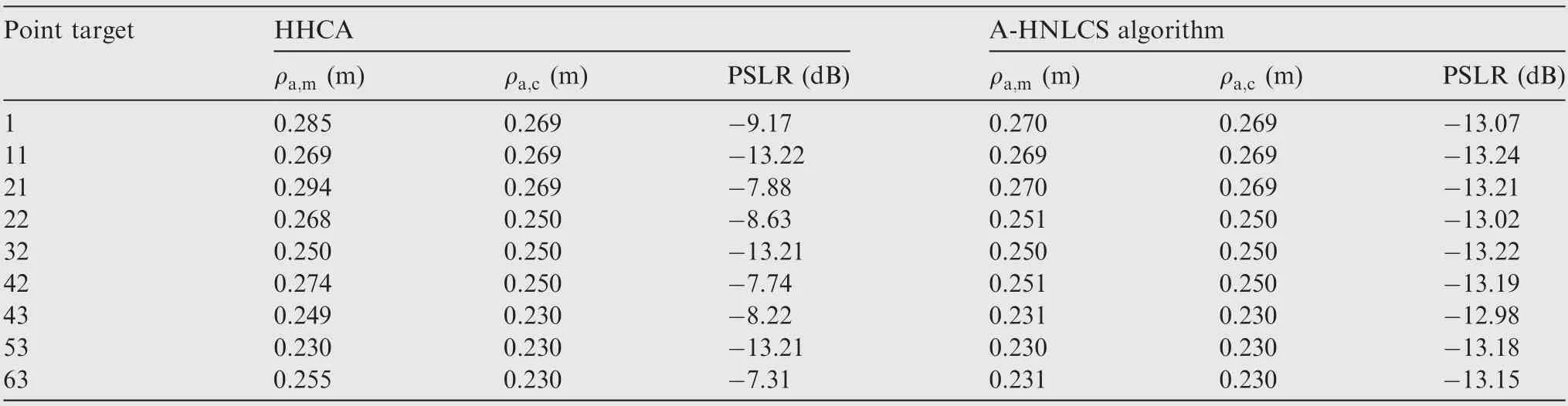
Table 2 Performance analysis of point targets.

Computational complexity of AHRE, A-NLCS, HHCA,and A-HNLCS is compared in Table 3. Times of both range Fourier Transform (FT) and azimuth FT for the above algorithms are the same because they all based on CSA. The proposed A-HNLCS requires the most complex multiplication.

The computation can be described as25:

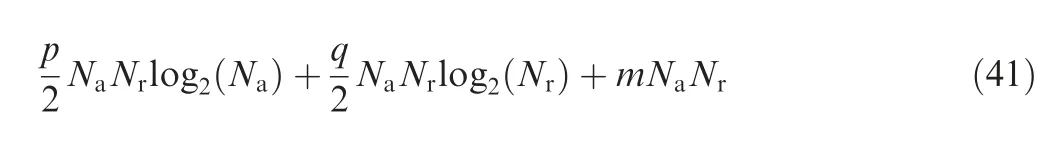
where p and q are the times of azimuth FT and range FT,respectively. m is the times of complex multiplication; Naand Nrare the number of samples in azimuth and range directions.

The proportion of computation and total computational operations of four different algorithms are shown in Fig. 12 for a range of Naand Nr. It indicates that FT always takes more than 80% of the computation for these four imaging algorithms, and the increasing complex multiplication of the proposed A-HNLCS would not cause much computation, as it is mainly dominated by FT. Furthermore, A-HNLCS can achieve the image of the whole scene instead of dividing the echo into several parts and stitching sub-images after processing. Hence, the increasing computational complexity of AHNLCS is acceptable to some extent.

Fig. 11 Azimuth profiles of point 1 and point 63 for HHCA and A-HNLCS algorithm.

Table 3 Analysis of computational complexity for different algorithms.

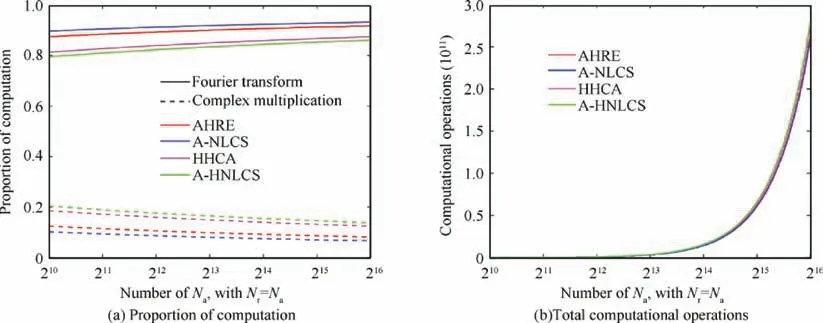
Fig. 12 Proportion of computation and total computational operations of four different algorithms for a range of Na and Nr.

5. Conclusions

As a trend for future remote sensing technology, highresolution wide-swath spaceborne SAR requires more precise range models and more effective imaging algorithms.

(1) Based on the analysis of azimuth-variance error in the range model, a second-order equivalent squint range model was developed to describe the range history for a larger azimuth swath.

(2) An advanced high-order nonlinear chirp scaling algorithm for HRWS spaceborne SAR was proposed,where sub-aperture processing was used to remove the azimuth variance and azimuth aliasing, the higher-order nonlinear chirp scaling algorithm was derived for accurate focusing, and the residual azimuth variance, imaging aliasing and geometric distortion were removed by a modified re-sampling operation.

(3) Simulation results have been provided to demonstrate the effectiveness of the proposed imaging algorithm.The proposed SOESRM and A-HNLCS algorithm can also be applied to other SAR systems where a larger azimuth swath is required.

Acknowledgement

This work was supported by the National Natural Science Foundation of China (No. 61861136008).

Appendix A. Approximate expression of SOERSM

Approximate expression Eq.(9)of SOERSM Eq.(7)is derived as following. The high order range model can be written as

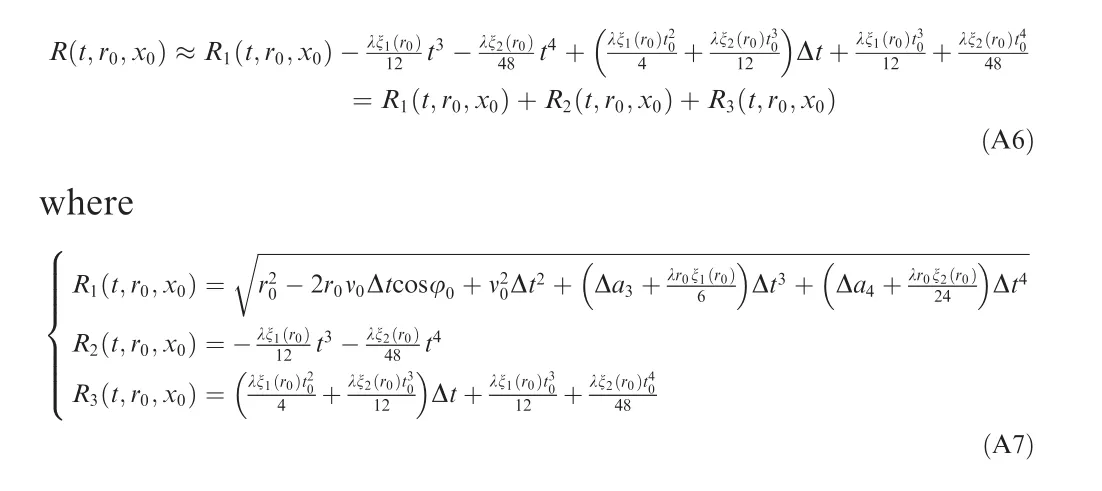
Appendix B. 2-D point target spectrum

2-D point target spectrum of the received signal are derived as following.

From Eq. (15), we have

Substituting Eq. (B5) to Eq. (B7), we have