Probabilistic fault recoverability analysis of flight control process

Yue PENG, Hao YANG, Bin JIANG

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

KEYWORDS Fault-tolerant control;Flight control process;Interconnected system;Probabilistic fault recoverability;Switched system

Abstract Probabilistic Fault Recoverability (FR) property reveals the capability of a system to accommodate faults under admissible input energy constraints in the sense of satisfactory probability.Motivated by the idea of probabilistic control methods,a class of admissible probability density functions is designed for detailed description of fault parameters,under which several probabilistic FR conditions are established. This significantly enlarges the range of recoverable faults obtained from the deterministic FR analysis. The tradeoffs between the risk of performance degradation and this increased recoverability margin are exactly achieved by allowing a small risk of FR violation. This paper analyzes the probability FR of dynamic systems with switching and interconnection characteristics, and applies the new results to several aircraft models including single longitudinal aircraft dynamic, Highly Maneuverable Technology (HiMAT) vehicle and meta aircraft. Simulation results show the efficiency of the proposed methods based on the comparison between deterministic and probabilistic cases.

1. Introduction

With the rapid development of aerospace industry in recent decades,Fault-Tolerant Control(FTC)has drawn great attentions due to the increasing demand for system safety. FTC aims to maintain overall system stability and acceptable performance in the event of potential failures.1Various FTC methods have been proposed for flight control processes whose dynamics are described by linear and/or nonlinear systems.2,3Due to more complex flying characteristics, the single models have also been extended temporally and spatially to switched and/or interconnected system models. For the former,switched system model arises naturally due to the existence of various jumping parameters in multi-mode flight control;4–6For the latter, interconnected system model often represents a system consisting of multiple dynamical subsystems that are coupled with each other such as meta aircraft configuration and cooperation of multi-vehicles.7–10

Fault Recoverability (FR), as the basis of FTC, evaluates the remaining controllability of a post-fault control system,and judges whether there exists an admissible control law subject to the input energetic constraints such that the post-fault system can still operate normally. Such a concept has been introduced and deeply analyzed in various dynamic systems.11–15The key tool behind these methods is using controllability Gramian, which a relation between the controllability and input energy consumption. The eigenvalues of controllability Gramian help to check whether the fault is recoverable under given energetic constraints.

However,the existing results of FR analysis only consider a space that contains all possible faults without taking into account the fault distribution probability in the space. This obviously makes the FR analysis conservative.In the practical situation, the fault distribution within a given range often satisfies certain probability characteristics,e.g.,less harmful faults are more likely to occur while the most serious faults rarely happen and often can be neglected even if they result in costly or permanent damage.16,17One may expect to relax the FR analysis by introducing the probability of fault distribution.

The well-known probabilistic control methods have been developed as effective tools to deal with complex uncertain systems where the probabilistic distribution of uncertainties is introduced.18–20Inspired by the idea of probabilistic control methods, this paper analyzes the probabilistic FR of linear,switched and interconnected systems with respect to input energetic constraints respectively.Since switched and interconnected systems cover time and space factors that a single linear system does not have, respectively, it is necessary to consider the probabilistic FR method in both systems. Besides, this topic is more meaningful in practical applications because of the increasingly complex flight control systems and missions.To the best of our knowledge, until now no result has been reported along this direction.

The considered faults in this paper are attached by a class of probability density functions, under which several probabilistic FR conditions are established which indeed enlarge the range of recoverable faults compared with the deterministic FR by allowing a small risk of FR violation.The probabilistic FR is thus a valid supplement and alternative of the deterministic FR. The proposed results are applied to several aircraft models including single longitudinal aircraft dynamic,HiMAT vehicle and meta aircraft.Detailed simulation results show the efficiency of the proposed methods. Such a new probabilistic FR evaluation scheme can be taken not only to adjust controllers, but also to redesign the system parameters such that the flight process is more reliable with respect to faults. In addition, the emergence of probability method increases the computational complexity and diversity of FR analysis of linear systems,which also lays a solid foundation for the analysis of the probabilistic FR of more complex systems such as nonlinear systems in the future.

In the rest of this paper,Section 2 addresses the probabilistic FR issue, Section 3 provides several aircraft examples, followed by some concluding remarks in Section 4.

2. Probabilistic FR analysis

2.1. Linear systems

Consider the following faulty linear system

where ε ≥0 denotes a small violation probability, that is, the probability of probabilistic FR conditions being violated for a set of random faults following the probability density function vector F.

Inequality (6) means there exists an admissible control under the energy constraint that can transfer the states to the origin with an acceptable probability risk. Compare inequality (6) with inequality (5), one can find that the range of recoverable faults determined by inequality (6) is enlarged.Such a range increases as ε gets bigger.When ε=0,condition inequality (6) is equivalent to inequality (5).

It should be noted that the functions satisfying Properties 1–2 are more reasonable than the uniform probability density function in the practical situation. Since faults can reduce the initial control effectiveness to a complete loss,the fault range is fixed within a bounded interval.Besides,we believe that probability density whose value is not always a constant depends on the magnitude of fault. That is, the more serious fault becomes,the smaller density turns.It follows from the Uniformity Principle proposed in Refs.21,22that

2.2. Switched linear systems

Consider a switched linear system taking the fault form

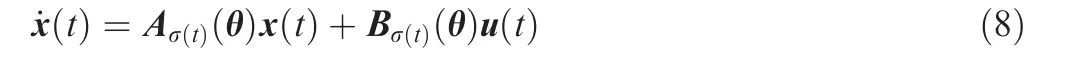
where x ∈Rnis the state vector, u ∈Rmis the input vector,θ ∈Δ is the fault vector under a probability density function vector F satisfying Properties 1–2. Define M≜｛1，2，...，M｝to represent the set of modes with M being the number of modes. σ:［t0，∞）→M denotes the switching rule, which is a piecewise constant function with right continuous.Note that the faults with the same probability density functions may exist throughout the whole switching process and may have different effects in different modes since Aiand Biare different for each mode.

Let ti, i=1，2，···, be the ith switching instant, and t0=0.Assume that the states do not jump at the switching instants.It follows that mode σ（ti）is activated in［ti，ti+1）,and switched into σ（ti+1） at ti+1. Let x（t0）=x0and x（tf）=xfbe the initial and final state of the system (8). The terminal time considered here is tfrather than ∞as in the single linear system and the interconnected system hereafter. That is because the time factor plays an important role in switched systems, and the switching time affects directly the probabilistic FR of switched systems.

Suppose that tfand σ（t）are given a priori.And let σibe the short form of σ（ti）.Given any x0and u,the solution of system(8) at tfis

Since the fault distribution is independent during the whole switching process, the input energy consumption of each period can be directly accumulated. Obviously, as the number of fault samples or switching modes increases, the integral and matrix operations become more complex. However, we only require the whole switched system to meet the probabilistic FR conditions,instead of individual each mode.Therefore,the flight control process modeled by switched system is more reliable and safer than that modeled by single system. Note that the fault distribution considered in this paper has nothing to do with time factor. That is to say, the distribution itself is memoryless.

2.3. Interconnected linear systems

Consider an interconnected linear system with N subsystems.Its connection behavior can be described by the directed graph G≜（N，E）, where N ≜｛1，2，···，N｝ is the set of nodes and E is the set of arcs. （j，i）∈E denotes the arc from node j to node i.This indicates that subsystem j is a neighbor of subsystem i in the sense that subsystem i can receive the information from subsystem j. Denote N（i） as the set of neighbors of subsystem i. The dynamics of subsystem i, i ∈N, can be written as

The purpose of dividing subsystems lies in finding each controllable groups, suppose that the following two assumptions are satisfied.

Assumption 2. For group i, i ∈L, the matrices Bdi（θi） and Gij（θi） satisfy

rank［Bdi（θi），Gij（θi）］=rank［Bdi（θi）］

where γijis the L2gain of the following system

Since fault distribution needs to be considered in multiple subsystems simultaneously, the computation becomes relatively complex compared with that in linear system. Beyond that, the input energy consumption in condition inequality(21)is related to the eigenvalues of the controllability Gramian and the control gain of each group, which also makes probability calculation more complicated.

3. Applications and simulation results

This section applies the proposed probabilistic FR evaluation methods to several aircraft examples, and provides detailed simulations results to verify the new results.

3.1. Single longitudinal aircraft dynamics

This example illustrates the result in Section 2.1. Consider a longitudinal aircraft model in Ref.11whose dynamics is described by

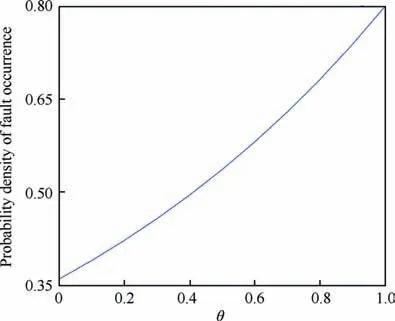
Fig. 1 Probability distribution of faults.

Without loss of generality, let the distribution probability functions of faults f1and f2take the exponential distribution form as shown in Fig.1.We shall give the comparison between deterministic FR method and probabilistic FR method. The range of ρ（x0，θ）over θ1-θ2plane is shown in both deterministic method and probabilistic method in Fig.2.It can be seen that fault parameters in the former are uniformly distributed,while in the latter the probability of fault occurrence decreases when θ varies from 1 to 0. This means that under the same energy constraint, the fault samples tolerated by the latter are more intensive, that is, the fraction of recoverable faults in the whole fault space are much larger. With the faults getting worse, more input energy is needed to accommodate faults.As is expected,θ1=θ2=0 brings to the worst-case scenario with energy requirement up to the highest.

Fig. 2 FR evaluation of single linear system.

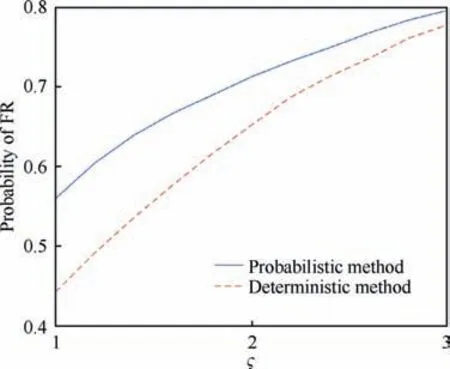
Fig. 3 Probability of FR in single linear system.

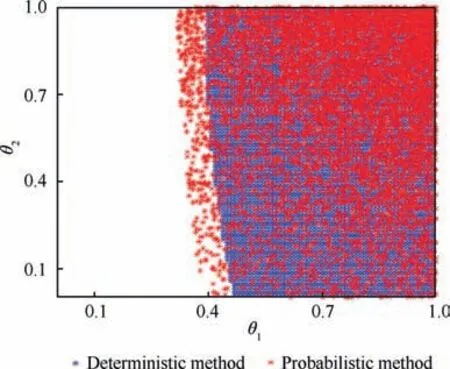
Fig. 4 Fault distribution under ς=2.2 and ε=0.05.

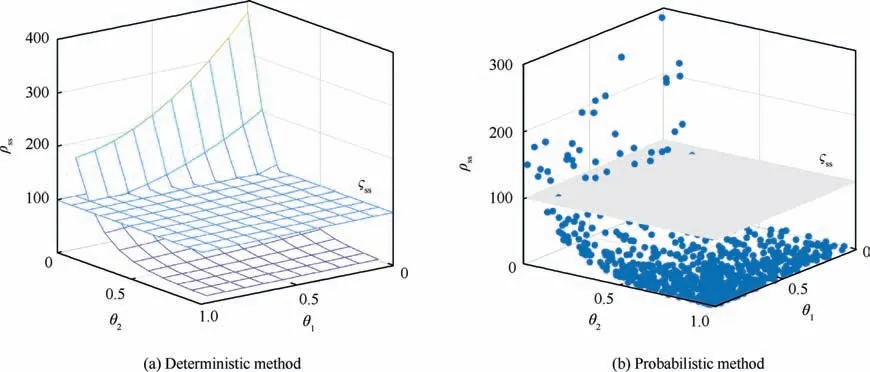
Fig. 5 FR evaluation of switched system.

Fig. 6 Probability of FR in switched system.

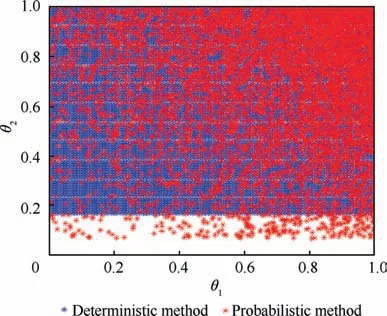
Fig. 7 Fault distribution under ςss =100.

3.2. HiMAT vehicle example

This subsection takes an example of full-envelope flight control process of the Highly Maneuverable Technology (HiMAT)vehicle in Ref. 6 to illustrate the result in Section 2.2. The dynamics of aircraft with long-range, multi-pose flight missions cannot be described by the single linear model due to various jumping parameters and changing environmental factors.The considered flight control process in this subsection is modeled by a switched system with 15 modes, where each mode represents an operating point whose dynamics are described based on their aircraft altitudes and velocities. Since the altitude and velocity could not vary discretely, the switching sequence is fixed.

The state-space description of the switched linear system is given by

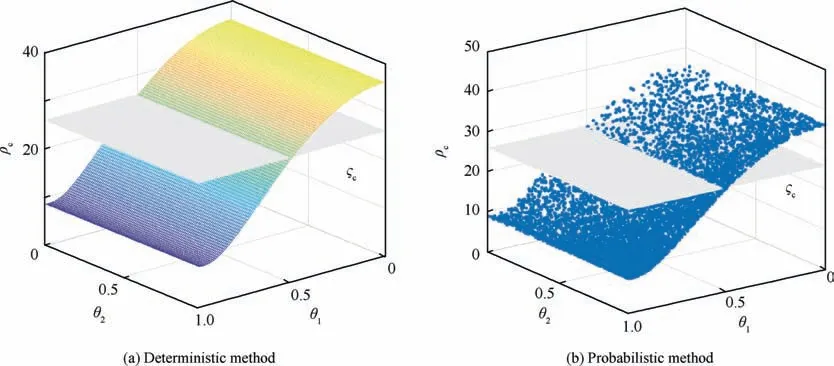
Fig. 8 FR evaluation in centralized structure.

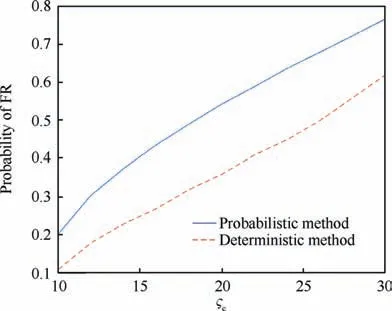
Fig. 9 Probability of FR in centralized structure.

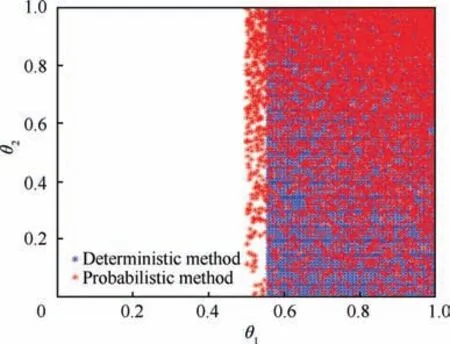
Fig. 10 Fault distribution under ςc =26.

Given an input energy constraint ςss=100,it can be drawn from Fig.6 and Fig.7 that the faults in the larger proportions of the fault space are recoverable under probabilistic FR(0.95)than that under deterministic FR (0.8).

3.3. Meta aircraft example

This subsection takes an example of meta aircraft in Refs.7,24to illustrates the result in Section 2.3. The meta aircraft is an integrated model composed of several individual aircrafts that are coupled with each other to form a wing-tip-to-wing-tip or tip-to-tail configuration through certain physical connection mechanisms. The interconnected system model is naturally used to describe the flight dynamics of meta aircraft.

The longitudinal aerodynamics of the meta aircraft in the wing-tip-to-wing-tip configuration is given as7:

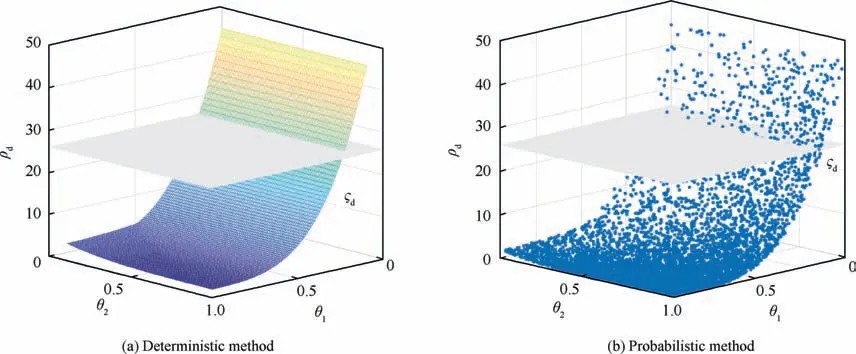
Fig. 11 FR evaluation in distributed structure.

Fig. 12 Probability of FR in distributed structure.

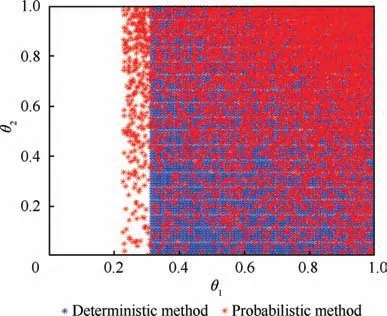
Fig. 13 Fault distribution under ς=2.2 and ε=0.05.

It is interesting and meaningful to compare the probabilistic FR in the centralized and distributed structures. Fig. 14(a)shows the probabilistic FR in the centralized and distributed structures under the uniform distribution of faults. One can see from Fig. 14(b) that the range of recoverable faults in distributed structure (more than 0.75) is larger than that in centralized structure (0.5). It indicates that under the same input energy constraint in this meta aircraft example, the FR probability in distributed structure is higher than that in centralized structure.

Fig. 14 Comparison between centralized structure and distributed structure.

4. Conclusions

This paper presents several probabilistic FR evaluation schemes for linear, switched and interconnected systems. The proposed methods are demonstrated by several aircraft examples,where the faults considered are subject to a class of probability density functions. This greatly enlarges the range of recoverable faults compared with the deterministic FR by allowing a small risk of FR violation. The future work will focus on probabilistic FR of more complex nonlinear systems with time-varying faults.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work is supported by National Natural Science Foundation of China (Nos. 61773201, 62073165), the 111 Project,China (No. B20007), and the Fundamental Research Funds for the Central Universities, China (No. NZ2020003).