Index allocation for a reusable LOX/CH4 rocket engine
Yi LI, Jie FANG, Bing SUN, Kiyng LI, Guoio CAI
a School of Astronautics, Beihang University, Beijing 100083, China
b Key Laboratory of Spacecraft Design Optimization and Dynamic Simulation Technologies (Beihang University), Ministry of Education, Beijing 100083, China
KEYWORDS Index allocation;Mass model;Multidisciplinary optimization;Reliability;Rocket engines
Abstract Reusable rocket engines are the core components of reusable launch vehicles, and have thus become a major focus of aerospace engineering research in recent years.In practice,subsystem design is based on the overall index allocation of an engine;therefore,a multidisciplinary optimization approach is necessary. In this study, design of a reusable methane/liquid oxygen (LOX/CH4)rocket engine with a gas generator cycle was investigated using multidisciplinary optimization.Two parameters were chosen as design variables: pressure and fuel mix ratio of the main combustion chamber. Optimization objectives were specific impulse, structural mass, and life cycle cost of the reusable rocket engine, and constraints were assigned to each discipline according to rocket design requirements. Then, an optimization model was developed, and optimal design parameters were acquired for the LOX/CH4 rocket engine.The proposed method is effective for designing the index allocation of reusable rocket engines and takes into account the multidisciplinary nature of complex systems.
1. Introduction
To date,the main focus of rocket launcher design research has been the reliability of liquid rocket engines,Refs.1,2 in particular, confirmation of the reliability index. Conducting reasonable programming tests is of vital importance, and confirmation of the reliability index can be incorporated into engine tests to uncover weak links.
The hot fire test is currently the only method used to confirm the system performance index, determine the limits of working conditions, and evaluate the reliability and lifespan of rocket engines. Owing to budget constraints, test run times are limited for single-use rocket engines,and only a small number of whole engine samples are available. Moreover, no systemic theoretical method has been established, as yet, to verify the lifespan and reliability indexes of reusable rocket engines.
Over the past few decades, key technologies related to subsystems and components of reusable rocket engines have been widely researched.3–5However, studies on the overall design parameters are still lacking. Furthermore, no suitable design criterion or corresponding fundamental theory and design method have been established for a complete reusable rocket engine system.
The analysis of reusable rocket engines falls within the scope of systems engineering. Typically, the main goal in conceptual design is the selection of reasonable parameters. To this end,optimization methods should be used in rocket engine design, owing to the strong interdisciplinary nature of the system.
Multidisciplinary Design Optimization (MDO) is usually used to ensure an optimal system design. In Refs. 6–8, MDO is defined as a methodology for design of complex engineering systems and subsystems that coherently exploits the synergism of mutually interacting phenomena. MDO has been widely used in aerospace engineering, especially in aircraft.9–14However,there is little reference using MDO in liquid rocket engine design.
Allocating specific indexes to the subsystems of engines,which must meet diverse requirements, remains a challenge in the overall design of reusable rocket engines. To date, the development of reusable rocket engine technologies has concentrated on the failure mechanism, life model, and structural optimization of components rather than a system-level index allocation that considers a maintenance strategy.
Herein, we investigate index allocation by applying a system engineering approach to reusable rocket engine design based on reusability and existing single-use rocket engine research. The remainder of the paper is organized as follows:Section 2 provides a brief introduction to the proposed index allocation system for a reusable rocket engine, elaborates the index system, and then presents mathematical models, including performance,mass,cost,reliability,and maintenance models; in Section 3, the MDO platform is described, as well as design parameters, multiple objectives, and constraints; optimum design is discussed in Section 4,and indexes are allocated to the subsystems; finally, main conclusions are listed in Section 5.
2. Index system
In contrast to single-use rocket engines, reusable rocket engines have longer designed lifespans and specific life index requirements, but must be recovered after each flight. Aside from lifespan,a number of additional technical indexes should be considered, such as performance, reliability, maintenance,and cost, as shown in Fig. 1. Numerous disciplines are involved, and therefore, combining various multidisciplinary requirements into a comprehensive reusable rocket engine design procedure presents significant challenges. In particular,enormous differences exist between the stages of model development within each discipline. To overcome this, mathematical models must firstly be established as the basis of optimization.
2.1. System performance model
In this study,a liquid rocket engine with a gas generator cycle was investigated. Generally, analysis of system performance mainly involves balancing system parameters,in this case,balancing the mass flow and the pressure, balancing the turbo power and the pump power, and establishing a relationship between the flows and pressures of various components.15
The total mass flow of the engine is the sum of the flows through the combustion chamber and the gas generator as

where ˙m is the mass flow, and subscripts c and g denote the combustion chamber and the gas generator, respectively.
The mass flow through the combustion chamber produces a thrust due to combustion, and the mass flow through the gas generator drives the flow through the turbocharger before the exhaust gas is expelled via the vent pipe. The mass flow through the combustion chamber is

where Iscis the theoretical specific impulse of the thrust chamber obtained using thermodynamic calculations; Fcis the thrust in the chamber;ηcand ηnare the efficiencies of the combustion chamber and the nozzle, respectively. The mass flow through the gas generator is an undetermined parameter equal to the turbocharger flow and can be calculated using the system power balance.
The pressure at the pump exit pepis equivalent to the sum of the pressure inside the combustion chamber pcand the pressure drop Δplbetween the pump exit and the combustion chamber including the pressure drops of the pipeline, valve,injector, and cooling channels as follows:

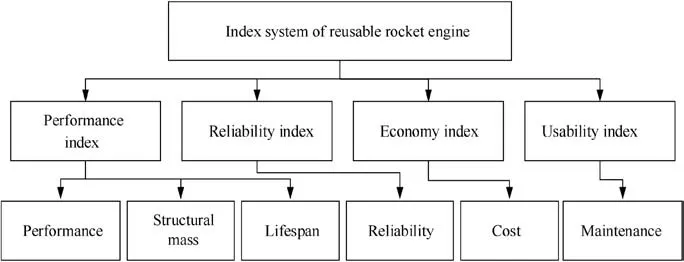
Fig. 1 Index system of a reusable rocket engine.
In general,the pressure at the pump entrance is specified in the overall design of the vehicle, and the total structural mass and cavitation inside the pump are considered.
The pressure at the turbocharger entrance pitis the difference between the pump exit pressure and the sum of the pressure drop for each component between the turbocharger entrance and the pump exit ∑Δpgias

The main parameters for the overall design of the reusable rocket engine are combustion chamber pressure,fuel mix ratio,area ratio of the exit to the throat of the nozzle,and back pressure of the nozzle at the design altitude. Further, numerous performance parameters can be used to create the evaluation index, such as thrust, specific impulse, effective load, and thrust-to-weight ratio. In this study, two parameters were selected to create the evaluation index.
The specific impulse of an engine is an important performance parameter,and the maximum specific impulse is the target of system design. For an open-cycle engine, the specific impulse is
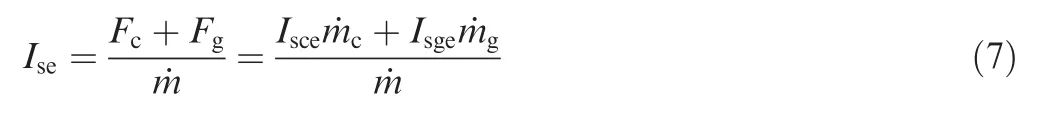
where Fgis the thrust of the turbocharger exhaust;Ise,Isce,and Isgeare the actual specific impulses of the engine, the thrust chamber, and the turbo exhaust, respectively.
Structural mass is another important parameter in engine design.Under the same thrust,carrying capacity can be greatly enhanced by a lower engine structural mass. The thrust-toweight ratio gradually increases as the engine thrust increases,which is also related to the propellant combination, start or shutdown time, and many other factors.
According to the balance model of the rocket engine,a simulation procedure is proposed to analyze the components of the engine. Input data includes combustion chamber design pressure, pressure at the nozzle exit for a specific design altitude,fuel mix ratio of the combustion chamber,fuel mix ratio of the gas generator, pressure in oxygen and fuel tanks, and rotational speeds of pumps.Based on these parameters,a performance evaluation index can be obtained.
Then,a system performance model can be created using the following steps:
Step 1. Calculate the thrust chamber thermodynamics to obtain the theoretical specific impulse and area ratio of the nozzle.
Step 2. Calculate the fuel and oxygen mass flows in the combustion chamber and the pump exit pressure.
Step 3.Calculate the gas generator pressure and confirm the thermal parameters of the gas.
Step 4. Calculate the turbocharger mass flow according to the power balance to obtain the nozzle thrust. Iterate until the entire thrust meets the required value.Thus,a performance evaluation index is acquired.
2.2. Mass model
A mass model is required to allocate indexes to components of the engine in order to perform the overall optimization. However,the mass of a liquid rocket engine is difficult to accurately determine because of numerous influencing factors.Therefore,the only method currently available to estimate the engine mass is based on existing statistical data and an empirical formula.16
Considering a liquid rocket engine with a gas generator cycle, the mass model can be expressed as follows:


2.3. Reliability model
There are two main methods for developing the reliability model, the mechanism model, and the statistical analysis model. The lifespan of a liquid rocket engine can have a relatively large distribution owing to differences in engine operating procedures and the quality of raw materials and processing techniques used to build engine components. During the design process,reliability analysis is typically based on statistical data of similar engines. Therefore, this was the method applied in our investigation.
In practice, the lifespan distribution of a liquid rocket engine and its components obey the Weibull distribution.17Hence, the probability density function is
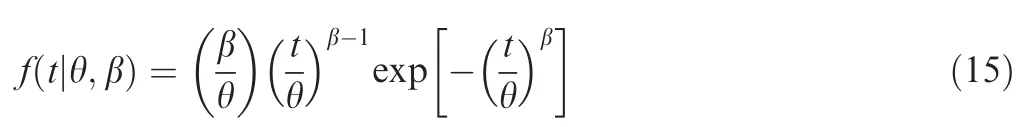
where θ is the scale parameter,also called characteristic life of the system, which reflects the average failure time of the system; β is the shape parameter; t is the working time of the engine. Furthermore, reliability is expressed as

System reliability of an engine depends on its subsystems.The series system is used in rocket engines since failure of any subsystem could cause the entire engine to fail. Thus,the reliability of the rocket engine is

where Ri(t)is the ith subsystem reliability,and n is the number of subsystems.
2.4. Cost model
The Lifecycle Cost(LCC)of a reusable rocket engine includes all direct and indirect costs of development,production,usage,and retirement.Development costs include design,testing,and evaluation of parts, whereas production costs are associated with the processing and assembly of the product. Usage costs include fuel, launch, retrieval, and maintenance costs.
The TRANSCOST model18–20was used in this investigation, which is one of the universal models for aerospace engineering cost evaluation. Within the parameter model, the TRANSCOST model has different Cost Estimation Relationships (CERs) for various costs.
The CER for development of the pump-fed liquid rocket engine can be expressed as

where f1is a correction parameter representing the technology readiness level, f2is the quality coefficient, and f3is an empirical parameter. f1is 1.25 for a firstly designed system, and the value could be 0.8–1.0 for a theoretically feasible system. f2is related to the reliability of the engine, for example, f2is 1.0 when the statistical reliability is about 0.995. The value of f3could be 1.1–1.3 (for new research teams), 0.9–1.1 (for teams with relevant experience), or 0.6–0.9 (for very experienced teams).
The CER for production of the reusable engine is

Cost of flight is the most complicated usage cost since both direct and indirect costs must be considered.Direct usage costs are associated with management of the launching site, operations before launch, flight control, propellant, and transportation to retrieve the engine. On the other hand, indirect costs are those related to administrative management of the launch site, technical support, equipment maintenance and depreciation,and spare parts storage and transportation.In summary,usage costs of the reusable rocket engine mainly comprise propellant, retrieval, and maintenance as

where Mpropis the total mass of propellant,L is the launch rate per year, and α is the volatilization intensity.
The propellant mass is connected to the mass flow and working time. Therefore, the equation for estimating the propellant mass can be obtained as follows:

where MCand MOare the masses of methane and oxygen,respectively, and ˙mCand ˙mOare the entire methane and oxygen mass flow rates, respectively.
Retrieval costs Crecare mainly generated by costs associated with searching for the engine, salvage, transportation,aftertreatment, and system checks. After retrieving the engine,blowing, drying, and system checks are needed, followed by maintenance. Therefore, the total cost for each retrieval is

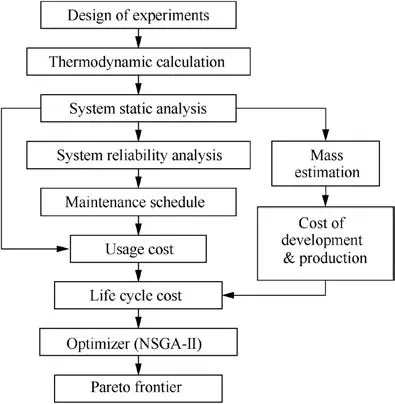
Fig. 2 System optimization design platform.
The maintenance cost Cmntis generated by the maintenance procedure, which has a close relationship with the selected maintenance strategy.
2.5. Maintenance model
Maintenance is necessary to keep a complex system in a reliable condition during the entire life cycle.Furthermore, maintenance is related to system reliability, effective age, and life cycle cost.In this study,a Preventive Maintenance(PM)model from Ref. 21 is applied in the usability index. In practice, PM includes a set of operations, such as periodical inspection,cleaning, lubrication, adjusting, and so on. In this paper, one typical PM action is taken into account to model the effect of maintenance to the engine, which is Maintenance Repair(MR).It includes activities of basic maintenance and repairing or replacing for some components.
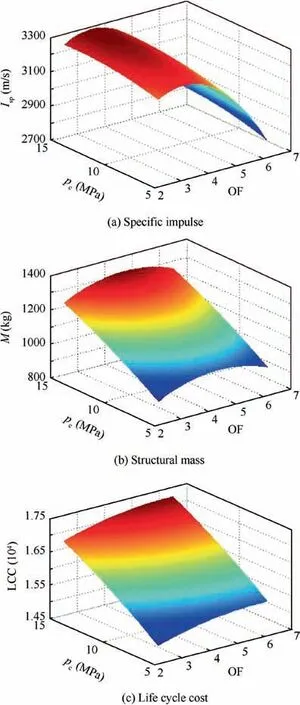
Fig. 3 Distributions of design objectives.
3. Index allocation based on multidisciplinary optimization
In engineering practice, the design of subsystems is based on the overall design index of the rocket engine. However, optimal design is difficult to achieve as a result of the complicated coupling relationships between different disciplines. Multiple attempts and many iterations must be performed before the final result is obtained. A single-disciplinary optimization method cannot be applied for the overall design of an engine since no reasonable scheme can be obtained without overlooking important coupling relationships and engine requirements.
Multi-disciplinary optimization is a methodology that fully explores and utilizes the interactions between subsystems to design complex systems. In addition, MDO uses numerical optimization and coordination methods to search for optimal parameters during the design process.
The entire design procedure is accomplished in three steps.
Step 1. System performance is analyzed to obtain system performance parameters that satisfy the specified requirements.
Step 2. Subsystem reliability characteristics are analyzed.
Step 3. A maintenance program is planned according to lifespan,and then the overall cost is determined.The reliability model is central to the framework by connecting the disciplines of performance, maintenance, and cost.
One major difference between a reusable rocket engine and a single-use rocket engine is the lifespan requirement. Several factors must be considered during the design of subsystem lifespan,such as complexity,importance,technical inheritance,and severity of working conditions, as well as the economic limitations of subsystems.After managing and balancing these factors,reasonable index allocation can be achieved.Additionally,life index allocation is difficult due to the scarcity of specific experimental data.Therefore,it is of significant importance to rationally and effectively allocate the system index using available techniques. As research continues,scientific methods could be utilized to modify model parameters with new information.

Table 1 Optimum design parameters and objectives.
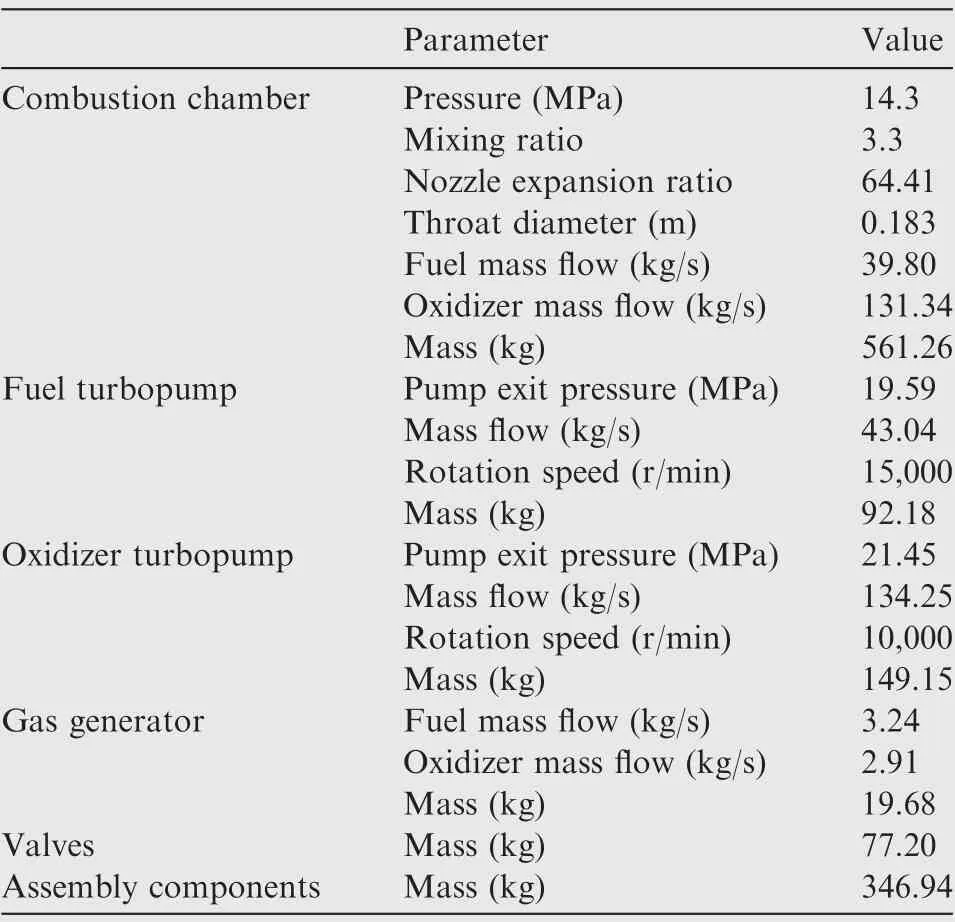
Table 2 Parameters of rocket engine.

Fig. 4 Maintenance of subsystems.
The index allocation platform uses a modular design method. Simulations were carried out in MATLAB. The optimizer is based on the model to search the Pareto frontier. The system design optimization platform is illustrated in Fig. 2.Overall, the lifespan cost comes from two areas: development and production cost, which can be determined by mass analysis,and usage cost related to the subsystem reliability and system performance parameters.
A methane/liquid oxygen(LOX/CH4)rocket engine with a gas generator cycle was investigated.The combustion chamber pressure pcand the mix ratio OF were selected as the optimization objectives and investigated at a given thrust for a designed altitude, lifespan, and reliability.
Based on the proposed model, a simulation of the static operating process was performed. Further, the relationship between the performance and reliability parameters was established, and the overall lifespan cost was estimated using the maintenance strategy as the cost model. The influence of optimization objectives on the design variables was investigated,and finally, an optimization was carried out using the genetic algorithm.
When designing a single-use rocket engine, performance is the main target.In contrast,lifespan is an important consideration in the design of a reusable rocket engine, and therefore,the life index is used as a constraint. Constraints can complicate the relationships between design targets. For rocket engines, a high-performance index also means a heavy structural mass and severe working conditions, as well as a low engine lifespan and poor reliability. Furthermore, frequent maintenance is required to ensure safe flight, significantly adding to costs.
After careful consideration, multiple optimization objectives were selected:maximum specific impulse,minimum structural mass, and minimum overall life cost. The life and reliability indexes were used as constraints during the optimization. The following mathematical expressions were used in the optimization:

where Ispis the specific impulse,T0is engine working time,N is the flight task number.
Multi-objective analysis of design variables aims to enhance the performance parameters while balancing tradeoffs between parameters.Since there is no definite optimal solution in multiobjective optimization, a decision-making method must be used to select the optimal design from the Pareto solution set according to a decision-maker’s preference. The Nondominated Sorting Genetic Algorithm (NSGA-Ⅱ) was applied in the multi-objective optimization process. The distributions of the design objectives are presented in Fig. 3.
In the design space, a single peak value of the specific impulse exists, 3284.27 m/s with a combustion chamber pressure of 14.4 MPa and a fuel mix ratio of 3.5. The combustion chamber pressure is the most important factor in the structural mass and the life cycle cost. Conversely, the fuel mix ratio has little effect on the structural mass and the life cycle cost.
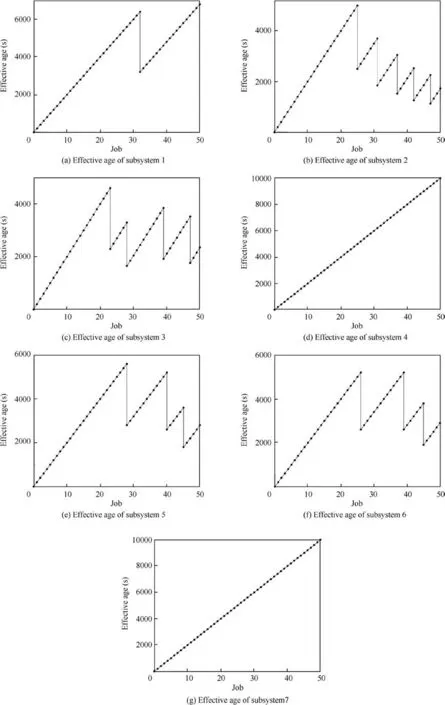
Fig. 5 Effective ages of subsystems.
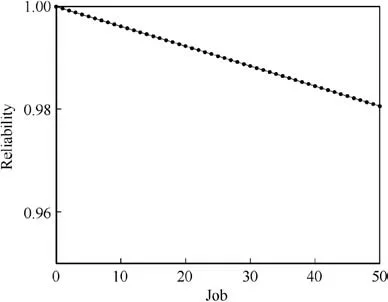
Fig. 6 Reliability of engine.
4. Optimal design and discussion
Selected from the Pareto front,optimal design parameters and objectives are listed in Table 1.
Based on the parameters listed in Table 1,the performance parameters and masses of subsystems are listed in Table 2.Maintenance schedules for subsystems are presented in Fig. 4. System reliability is guaranteed by ensuring sufficient maintenance. Subsystem numbers from 1 to 7 represent the thrust chamber,the fuel pump,the fuel turbine,the gas generator,the oxidizer pump,the oxidizer turbine,and the feed system, respectively.
Effective ages of each subsystem are shown in Fig. 5.According to the maintenance model,maintenance operations could reduce the effective ages of components.In other words,a subsystem essentially becomes newer after a maintenance operation.Additionally,the turbopumps require more maintenance than those of other subsystems to meet system reliability requirements. The maintenance intervals become shorter because of the characteristics of the Weibull distribution.Reliability of the entire engine is shown in Fig.6.Reliability of the entire system gradually decreases as the flight job continues,but the reliability index is still above 0.98, which is the constraint of MDO.
5. Conclusions
(1) There is a restrict relationship between the lifespan and the maintenance index, which can affect the total life cycle cost. Designers must balance the performance and cost indexes to ensure reliability throughout the entire engine life cycle.
(2) Results for the maintenance index suggest that the fuel and oxidizer pumps require more maintenance operations to ensure the reliability of the overall system.The subsystem maintenance interval between flights was obtained using the maintenance model presented in this work.Owing to characteristics of the Weibull distribution, the maintenance intervals become shorter.
(3) The index allocation model established in this study meets the multi-disciplinary requirements of the overall engine design, for which the reliability model is central.Multi-objective optimization is a comprehensive assessment that can be used to effectively select an integral set of design parameters for subsystems, including performance, lifespan, and maintenance.
(4) A reusable LOX/CH4 liquid rocket engine was designed using MDO, and the indexes of subsystems were allocated according to the mathematical model. The combustion chamber pressure is 14.3 MPa, and the mixing ratio is 3.3. The specific impulse is 3106.28 m/s. The entire methodology could be widely applicable in a reusable rocket engine design process.
 CHINESE JOURNAL OF AERONAUTICS2021年2期
CHINESE JOURNAL OF AERONAUTICS2021年2期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Recent active thermal management technologies for the development of energy-optimized aerospace vehicles in China
- Electrochemical machining of complex components of aero-engines: Developments, trends, and technological advances
- Recent progress of residual stress measurement methods: A review
- Micromanufacturing technologies of compact heat exchangers for hypersonic precooled airbreathing propulsion: A review
- Towards intelligent design optimization: Progress and challenge of design optimization theories and technologies for plastic forming
- A combined technique of Kalman filter, artificial neural network and fuzzy logic for gas turbines and signal fault isolation
