关注本质 促进理解

殷芊

[摘 要]基于儿童理解的数学教学，在儿童的天性和数学学科本质之间架构起一座桥梁。以“小数的意义”教学为例，鼓励儿童用自己的方式表征数学本质，丰富儿童对数学知识的理解，真正实现“数学必须成为儿童经验的一部分”。

[关键词]数学本质;数学理解;个性表征

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2021）11-0015-03

一次试教结束后，我正在为课堂上活跃的气氛和流畅的师生应答而心满意足，“课堂看似活跃了，学生的思维‘沸腾了吗？关于小数的意义，学生真的理解了吗？”师父提出了两连问 ，“你用题目‘1时-0.1时=（    ）分测试看看。”测试结果令我无地自容：全班45人，做对的仅有21人。显然，学生只是记住了某一情境下的小数的意义，并没有深刻理解其本质。

当我自认为已经帮助学生扫清知识的盲点，清除了理解的障碍时，一道题的测试结果就反映了很多学生对于小数意义的理解是模糊的，只是停留在机械模仿层次。仔细分析测试的数据和结果：有15人不约而同地填写了“1”，显然不是巧合，他们的根据是 “0.1元=1角，0.01米=1厘米”。究其原因，学生在学习小数意义后，只记住了某一特定情境下的小数意义，无法实现对小数的抽象意义与生活意义的深刻理解。

【教学改进】

纵观几个版本的教材的结构和数学知识的结构体系，第一学段是让学生结合具体的生活情境初步认识小数，第二学段要求学生理解小数的意义，即小数的实质是十进分数的另一种表示形式。因此我由“经验回忆，与小数的初次相遇”“个性表征，深度对话小数的意义”“动态演示，揭秘小数的产生”和“场景体验，触摸真实的小数”四大板块入手，以小数单位作为生长点，引导学生在不断细分的过程中掌握小数的意义。

片段一：经验回忆，与小数的初次相遇

师：三年级的时候我们就已经学过小数，现在让我们一起回顾当时的研究过程。把这个正方形当成“1”，瞧，把它怎么样了？（图略）

生1：平均分成了10份。

师：涂色的部分可以用什么数来表示？

生2：0.4。

生3：[410]。

师：[410 ]= 0.4。

师：这是一条线段，把它平均分成10份，你也能说出类似的等式吗？

生4：[210=0.2]。

师：观察这些等式里的分数和小数，有什么发现？

生5：右边都是一位小数，左边都是十分之几的分数。

生6：一位小数就表示十分之几。

师：当表示的部分不满“1”时，我们是怎么办的？

生7：把1平均分成10份。

师：是的，把1平均分成10份。每份就是[110]，就是0.1。

基于学生已有的学习经验，从面积模型到线段模型，帮助学生的学习跳脱“量”的形式，使学生直面“数”的本质，想起与小数初次相遇的情形。

片段二：个性表征，深度对话小数的意义

师：如果还用这个正方形表示“1”，你能画图表示0.44吗？

生1：先涂上4条，是0.4，再把一个0.1平均分成10份，涂上4格就是0.04。合在一起就是0.44。

师：为什么要把0.1平均分成10份呢？

生1：因为现在的分法只能表示多少个0.1，0.44中的0.04没有满0.1。

师：不满0.1时，继续把0.1平均分成10份，每份就是0.01。

师：实际上，我们把这个正方形平均分成了多少份？

生2：先把它平均分成了10份，接着将每一条又平均分了10份。10×10 =100（份）。

师：那这里的1小格就是多少？

生3：[1100]，也就是0.01。

当学生在课堂上表达自己心目中的“月亮”时，教师常常想的是自己设定的“月亮”，之后就以自己的声音取代了学生的思考和表达，殊不知，每个人都有自己对于“月亮”的理解。在这个环节中，面对大任务“你能表示出0.44吗？”，基于已有的经验，学生将自己对两位小数朦朦胧胧的感觉表征出来，通过这种表征，教师就有机会看到不同层次的学生的数学理解和思考轨迹。

片段三：动态演示，揭秘小数的产生

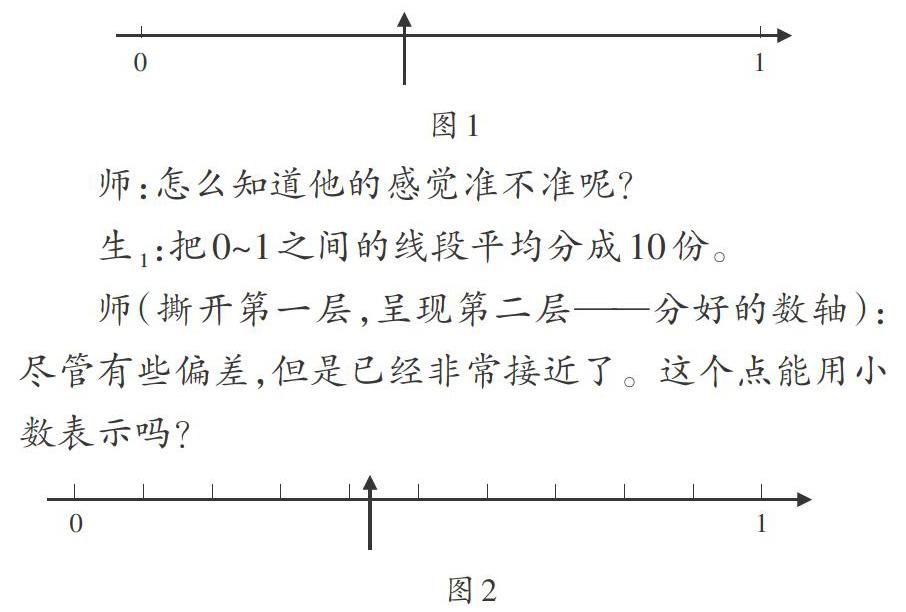
师：我们在分一分、涂一涂正方形的过程中认识了小数，能在数轴上找到这些小数吗？0.4在哪？（学生凭借对小数的估计在数轴上指;如图1）

师：怎么知道他的感觉准不准呢？

生1：把0～1之间的线段平均分成10份。

师（撕开第一层，呈现第二层——分好的数轴）：尽管有些偏差，但是已经非常接近了。这个点能用小数表示吗？

生2：能。把0.4～0.5这一段平均分成10份。

师：我们放大来看这个点究竟表示多少。

师（若学生标的正好在两位小数的格子线上，则教师在格子中间点一个点）：如果这个点在这里怎么办？

师（若学生标的不在格子线上）：怎么办？

生3：继续把0.45～0.46这一段平均分成10份。

师：这是把1平均分成多少份？每份是多少？

生4：把1平均分成[11000]份，每份是0.001。

师：这时产生的是几位小数？

生5：三位小数，三位小数表示千分之几。

师：小数就是在这样不断细分的过程中產生的，小数的产生离不开分数。

将学生喜欢探秘的心理特点与数学知识融合，让学生凭着自己的感觉在一根数轴上找表示0.4的点，学生感觉的偏差为接下来的教学提供了素材。在动态的揭秘过程中，小数产生的过程就是将一个个单位不断细分的过程。为什么要平均分10份、100份、1000份呢？究其原因，是为了和整数的计数原则十进制一致。

片段四：场景体验，触摸真实的小数

师：小数在生活和生产中有什么作用呢？我们来看一些画面（如图3）。这些画面中出现了很多的小数，我选出了2个小数和大家分享。0.004 mm是什么？

生1：基本的装配精度。

师：0.005 mm是生产的小小偏差，与0.004相差多少？

生2：0.001 mm。

师：想象一下，0.001 mm有多长？

师（出示：0.001 mm相当于一根头发丝直径的四十分之一）：就这么微小的差距，在天文学意义上40个月亮都找不着了。我们在精益求精的工匠精神中再次感受到了小数的魅力。

数学知识要回归真实的世界中，学生的学习才算完整。工匠们生产精密零件时， “精益求精”四个字将小数的本质与价值发挥得淋漓尽致。基于真实的场景体验，学生触摸到更加鲜活、有趣的知识与文化。

【教学反思】

数学理解的目标指向具有两重内涵：一是“对数学对象的理解”，理解数学知识的内容、方法技巧、策略思想;二是“从数学的角度去理解现实”，这是学生内心深处更深层次的数学观念的转变和形成。学生的真学习应该基于灵动的经验，亲历研究的全过程，体验真实的问题。

1.“鼓励个性化的表征”，尊重灵动的儿童经验

教师习惯于硬“赶”着把教学内容传递给学生，急“赶”着把少数学生研究成功的结果呈现在全体学生面前，没有给足学生静静思考的时间和空间。

对于同一概念，学生有不同的想法和表达，教师应该充分给予他们表达“我知道了什么”的机会。在如何表示“0.44”的环节中鼓励学生用自己的经验表达数学观点，在深度对话交流中找到不同经验间的本质联系，在比较沟通中达成对已有经验的改造、生长和建构，从而有了对“0.44的不同表达”。

2.“追溯知识发展的脉络”，亲历完整的数学化過程

“数学家是怎么研究的？”“为什么有了分数还要有小数呢？”学生似乎一直关心这样的话题。因此，教师要让学生经历“沿着数学家的脚步”的研究过程，一次次地尝试、突破。

看似简单的知识往往背后蕴含着深刻的数理，教师应该带领学生突破表层，围绕“小数是怎么产生的”这一主题进行探究，经历发现问题、解决问题的过程，学生就能在创造和感受动态揭秘的过程中不断接近对小数意义的本质理解——小数就是在不断地细分过程中产生的。此时，学生完全是探索者和发现者，不仅完整经历了对小数的认识、理解与表达的过程，更深切体会到小数是在怎样的情形下诞生的。

3.“基于真实任务的问题解决”，体验有意义的数学理解

真实的任务和真实的问题能为学生提供一个促进知识向日常生活转化的实践场。在这实践场中，知识、思维和学习的情境是相互联系的，学生的信念和经验构成解决问题的工具。例如，看到工匠制造精密仪器，学生的脸上充满着惊讶，短短的30秒钟，不仅“有看，有听”，更融合了学生对小数意义浸润式的思考。在忠实于数学的本质基础上，不拘泥于学科的束缚，真正实现用数学理解世界，学生对于小数意义的理解才能从形式走入更大的文化背景中。

“让儿童成为教学中最亮丽的风景线”不是一句口号，需要教师不断追问和思考，摆脱课堂中一些“套路”，助力儿童的数学理解。

（责编 金 铃）