一类具有Logistic增长和病毒变异的SEIR传染病模型的稳定性分析

梁桂珍,方慧文,2,王伟杰

（1.新乡学院数学与统计学院,河南新乡453003；2.郑州大学数学与统计学院,河南郑州450001）

长期以来,人们与各种疾病做着不屈不挠的斗争,传染病的防治仍是当前世界各国公共卫生工作的重要内容之一.在传播过程中,传染病往往随着病情的发展,病毒自身易发生变异,则易导致疾病失控[1].如每年爆发的流感会以其中一种病毒形态表现出来,发作的病毒毒株还会发生或大或小的变异,也可能两种病毒同时发作.近年来,数学模型已成为研究传染病的重要工具,预测每次到来的传染病疾病的流行趋势[2-6].通过对传染病模型的动力学分析,将对了解疾病,控制病毒传播提供强有力的理论依据.通常我们研究的是具有潜伏期的单独存在的病毒传染的SEIR模型,现今研究具有病毒变异的论文还不多.傅金波等[7]、吴红良等[8]、程晓云等[9]分别研究了具有logistic增长的SIRS、SIR、SIQS传染病模型的稳定性分析；Andrei[10]研究了具有多种病毒传染的SEIR传染病模型,患有多种不同病毒的染病者均具有传染能力,多种不同病毒是单独存在的,之间不是变异的关系,得到了模型全局性态的结果；李冬梅等[11]建立了潜伏期具有常数输入率的SEIR模型,得到了模型仅存在地方性平衡点,并且是全局稳定的结论.传染病在传播过程中,病毒易发生变异,会对疾病防控产生一定的影响,研究带病毒变异的模型,能够了解疾病传播规律,为采取科学有效的防控措施提供理论依据.

1 模型建立

有些传染病在传播期存在一定的潜伏期,易感者染病后在一个周期内才会显现出来.在疾病传播的过程中,病毒易发生变异.在本文中,将人群分为易感者、潜伏者、感染者和恢复者,其中感染者分为病毒变异前的感染者和病毒变异后的感染者,他们均具有感染性.我们假定只有易感者具有生育能力,并考虑环境容纳量这一因素,则易感人群增长量为Logistic增长,建立的模型为

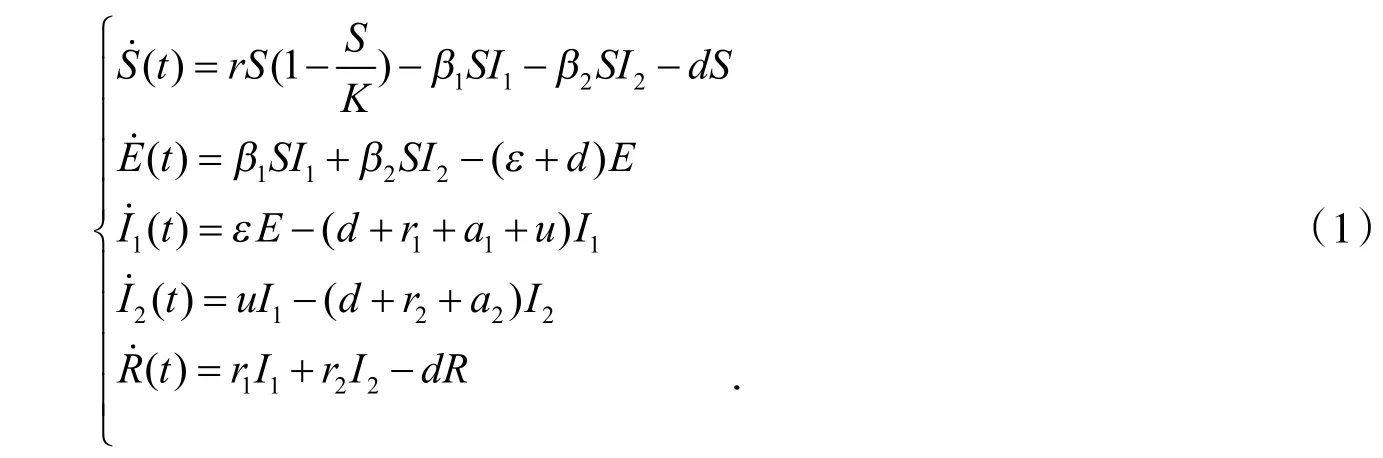
式（1）中：S = S( t), E = E( t), I1=I1(t), I2= I2( t), R =R( t ),分别表示t时刻易感者、潜伏者、变异前病毒的感染者、变异后病毒的感染者、恢复者的数量,K表示环境容纳量,d表示种群的自然死亡率,ε是潜伏者转变成变异前患者的比率系数,u是变异前患者转变为变异后患者的比率系数,β1和β2分别表示变异前患者和变异后患者的传染率系数,γ1和γ2分别表示变异前患者和变异后患者的恢复率系数,a1和a2分别表示变异前患者和变异后患者的因病死亡率系数.为了使模型具有生物意义,该模型的所有参数都为正.

模型（1）的前四个式子不含R,现考虑传染病模型

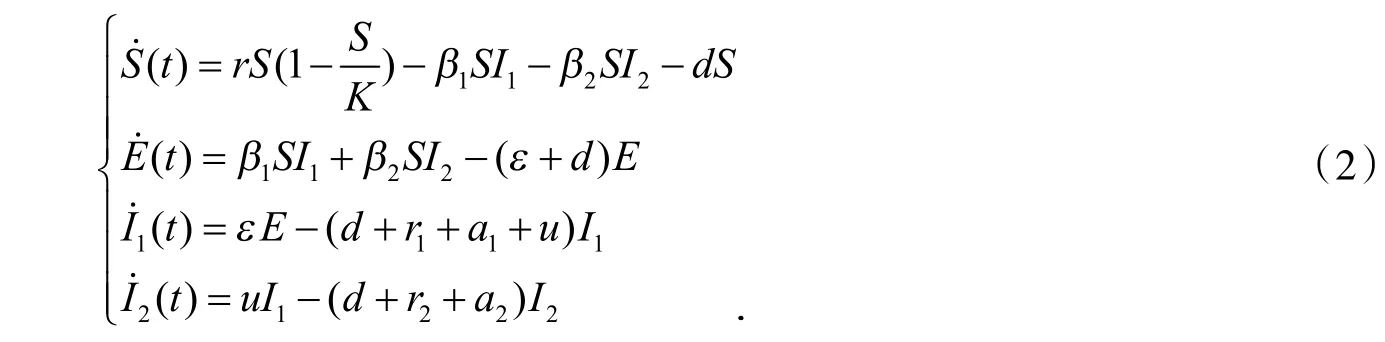
显然,模型的正向不变集为

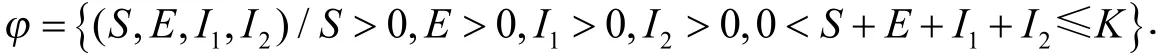
2 模型平衡点的存在性

3 平衡点的稳定性

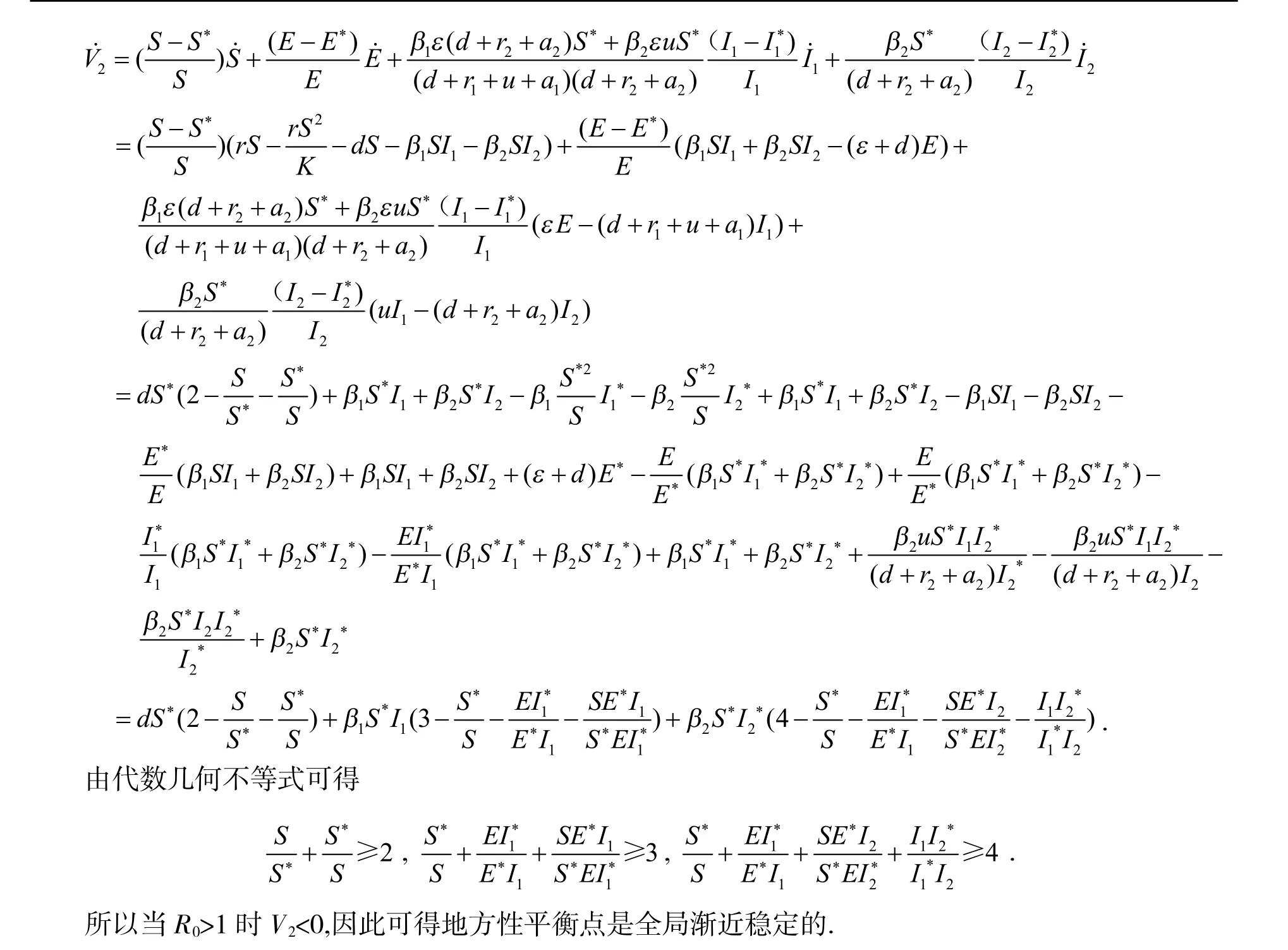
4 数值模拟

通过数值模拟来验证模型（2）中无病平衡点的渐近稳定性,令参数K=4,r=0.5,β1=0.1，β2=0.2,d=0.2,ε=0.5,r1=0.8,r2=0.3,α1=0.01,α2=0.02,u=0.3则 基 本 再 生 数R0=0.28＜1取S（0）=0.3,E（0）=0.5,I1（0）=0.1,I2（0）=0.1并利用Matlab软件进行数值模拟,得到模型（2）解的渐近稳定性态见图一,表明模型（2）的无病平衡点是全局渐近稳定的,即疾病最终消除.

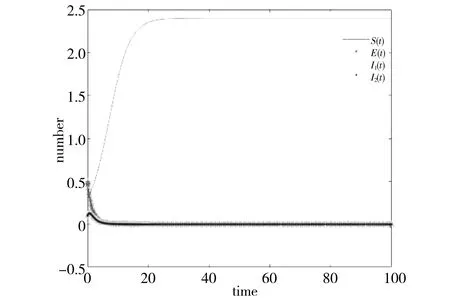
图1 无病平衡点的稳定性Fig.1 Stability of the disease-free equilibriumpoint

同理,令参数K=2,r=0.2,β1=0.5,β2=0.4,d=0.1,ε=0.7,r1=0.5,r2=0.1,α1=0.01,α2=0.02,u=0.3则基本再生数R0=4.02＞1,取初始条件S（0）=0.3,E（0）=0.5,I1（0）=0.1,I2（0）=0.1并利用MATLAB软件进行数值模拟,得到模型（2）解的渐近稳定性态见图2,表明模型（2）的地方病平衡点是渐近稳定的.

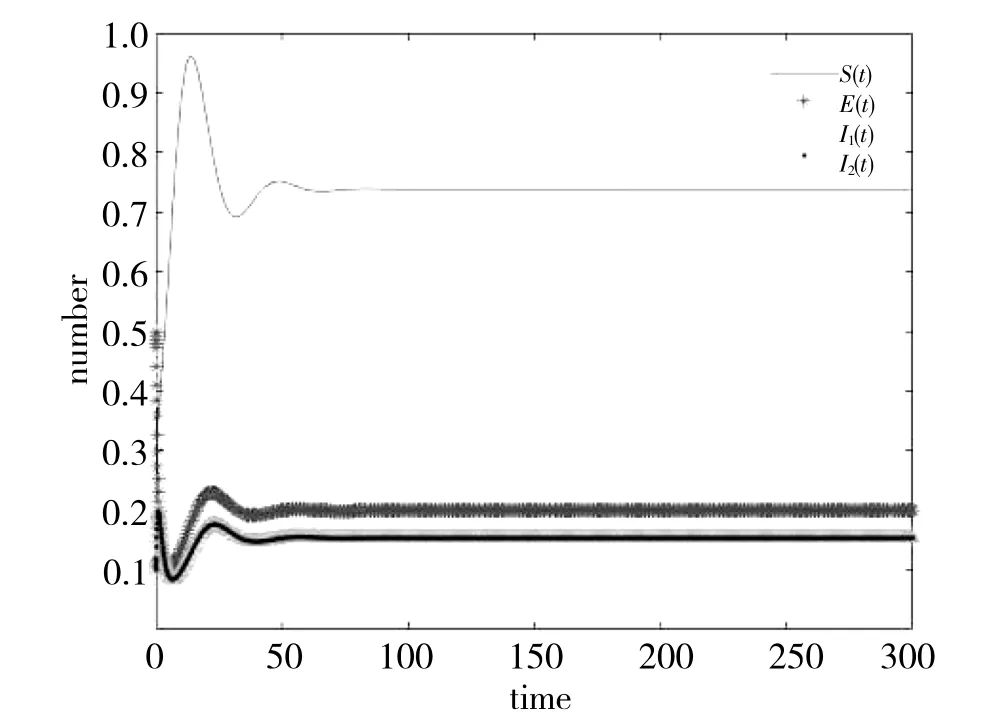
图2 地方病平衡点的稳定性Fig.2 Stability of the endemic disease equilibriumpoint

5 结论与展望

本文利用数学模型,研究了一类具有Logistic增长和病毒变异的SEIR传染病的传播和影响.通过对模型分析得到了该传染病绝灭与否的基本再生数的表明表达式,证明了以下结论,当R0＜1时,无病平衡点P0（S0,E0,I10,I20）是全局渐近稳定的,即传染病最终消除；当R0＞1时,存在唯一地方病平衡点P*（S*,E*,I1*,I2*）是全局渐近稳定的,则疾病将流行.我们还通过数值模拟验证了结论的正确性,对具有病毒变异的传染病的防控提供了理论依据.但是在我们的模型中假设只有易感者具有生育能力,而垂直传播的因素的影响还需要在我们今后的工作中进一步的进行研究.