对培养学生“思维深刻性”的探讨
别义利
小学数学不单纯是为了传授数学知识,更重要的是为了培养学生的能力,发展智力,开发创造力,思维能力是一切能力的核心。在小学数学教学中,如何加强思维训练,发展学生思维能力的问题已成为广大教师关注的热点课题。但是如何培养学生思维深刻性的品质呢?
思维深刻性表现为善于透过问题的表面现象而深入其本质,揭示现象所产生的原因和结果,而不是停留在事物的表面现象和外部联系上。在教学中应时刻注意培养学生思维深刻性的品质,提高其数学思维能力。在教学中我发现:恰当地创设思维情境,是培养学生思维深刻行之有效的方法。下面就自己的教学体会谈一谈粗浅看法。
一、培养抽象概括能力
思维深刻性高的人具有较强的抽象概括能力。而数学学科的特点之一就是高度的抽象性。可见培养学生的抽象概括能力尤为重要。在教学中可结合教内容选用具体实例创设思维情境,引导学生深入观察,运用逻辑方法抽象概括问题的本质属性,以培养学生的抽象概能力。
比如:教师在黑板上画一个正方形后,告诉学生把一个正方形各边中点依次相连又成为一个正方形。紧接着提出问题,引导学生进入思考:你们发现了哪些结论?若是不断地将正方形各边中点连接下去呢又会有什么结论?通过学生的观察,使学生直观形象地从每一个正方形变化规律概括出:“连接正方形各中点所组成的正方形面积减少一半,三角形个数增加4个,不断地将正方形各边中点连接下去所组战的正方形面积将形成等比数列”。这样不仅得出抽象的数学结论,而且学生也学会使用抽象概括的方法,理解的透彻并且深刻,从而培养了概括思维能力。
二、用不断追问引导学生对问题进行层层深入的思考
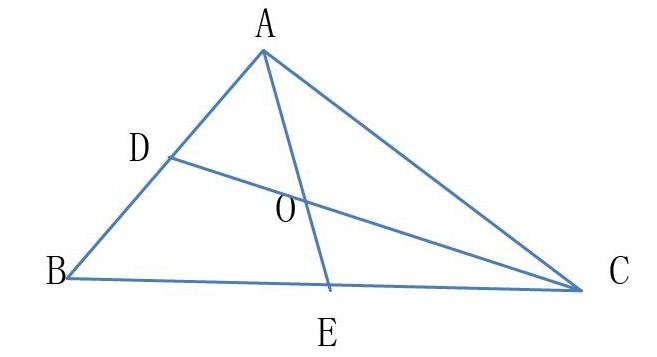
在教学中根据学生实际,通过对问题增加条件,减少条件进行变化,提出一连串问题使问题发展变化。促使学生学会层层深入地思考问题。例如在下图中:任意△ABC,D、E分别为中点,那会有什么结论?△AOD的面积与△OEC的面积相等吗?若连接DE,能说明上面的结论吗?如果连接OB,又可得到什么结论?四边形DOEB的面积与△ABC的面积是什么倍数关系吗?若取AC边上的中点G,连接DE、DG、GE,那么△DGE与△ABC具有相同的性质吗?等等。象这样随着题目的演变,问题越来越深化,使学生对于数学问题的思考也能够抓住问题的本质和规律深入细致地加以解决。
三、在解题后帮助学生总结规律和方法
在教学中经常发现有些学生题目做了不少但是收效甚微。我听到有的学生提出过这样的问题:“老师,能不能少做些题,而思维能力更强呢?”为什么他们会提出这样的问题?究其原因主要在于这些学生不能归纳总结解题的基本规律,认识不到题目之间本质的联系。针对这种情况,教师可根据題目的特点,在学生解题之后创设情境,帮助学生归纳总结解题规律和方法,把获得的知识和方法迁移应用于解决其它问题之中。例如下面三道题:
1、甲库中有化肥1700袋,乙库中有化肥1050袋。若每天从甲库中运出50袋,从乙库中运出30袋,多少天后两库中化肥袋数相同?
2、花布是白布的2倍,若每天卖出30米白布和40米花布,几天后,白布全部卖完,而花布还剩120米。原有花市多少米?
3、小明的储蓄箱已有4.8元,小强的储蓄籍已有9元。现在小明每天放入3角,小强每天放入8角,问多少天后小强的钱数是小明的2倍?
在学生解题之后,教师提出问题:这几道题中有哪些相同之处和不同之处?你从中得到哪些启发?这样让学生透过实际意义不同的表面现象,而抓住它们的本质联系,即都是“按两个差求未知数”。使学生养成注意从本质上解决问题的习惯,既提高了解题能力又培养了学生思维深刻性的品质。
(北京市顺义区张镇中心小学校)

