知识图谱导向下的有理数单元整体教学

摘 要:有理数的教学内容包括有理数的概念、性质和运算.教师要厘清概念教学的脉络,构建“知识图谱”,解构教学目标,解析教学重难点,重构教学设计,实现精准教学,使核心素养在课堂教学中真正落地.
关键词:有理数教学;知识图谱;教学目标
有理数教学是初中数学教学的起点.在小学阶段学生已经初步学习了负数,但无论是理解运算对象,还是掌握运算法则和选择运算方法,初中的要求都大大提高.初中阶段学生除了会算还要进一步学习“优算”,教师要设计运算程序,使学生算有方法,算有规矩,要探究运算思路,使学生算得合理,算得简洁,进一步学习数系扩充的方法,掌握研究一类数的基本方法.因此有必要把有理数的教学设计置于数系扩充的主题整体设计,使运算核心素养真正地为进一步学习初中数学奠定基础.
一、把握有理数的知识图谱是教好有理数的开端
(一)有理数的“知识图”(以下简称“图”)
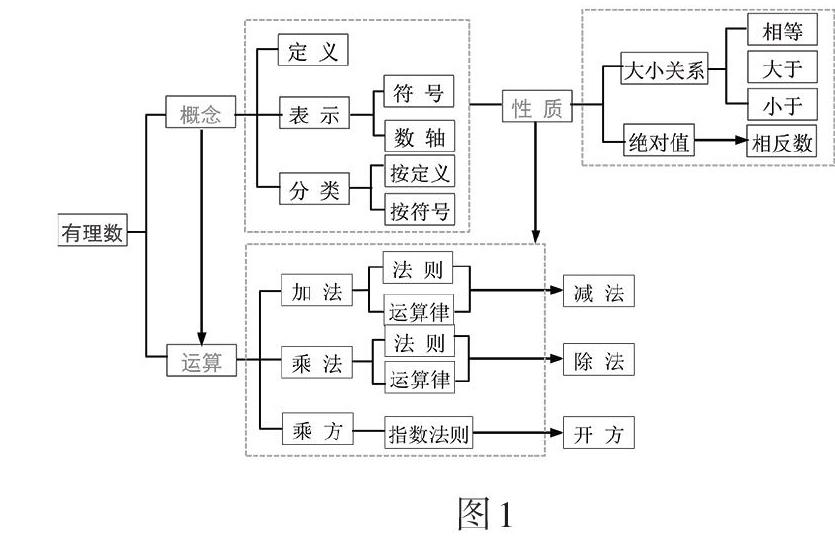
图1清晰地表明有理数学习的内容:有理数的概念、性质和运算.学习的线索:概念→性质;概念(性质)→运算→应用.教学的重点是有理数的概念(主要是负数的概念)、有理数的性质和有理数的运算(负数参与的运算).概念教学的难点是负数的引入;性质教学的难点是数形结合(数轴如何引入?)思想的第一次渗透;运算教学的难点是负数参与的运算规律的归纳获得.
(二)有理数的“知识谱”
“图”能让教师整体把握章教学的关键内容和结构体系,有利于单元整体教学的实施.但每个知识点到底要把握到什么程度,“图”中难以看出来,这就要求在“图”的基础上,对具体的知识点进行更为精准的描述.这便是如表1所示的“知识谱”(以下简称“谱”)的意义.从“谱”中可以看到,“知识点目标”就是对课程标准单元目标进行更为具体、更为详细的行动描述,使得知识点的教学目标变得具体、“可操作”、“易检测”.这样的目标分解可以使教师备课和制作质量检测工具具有高度的一致性,也使得教师的教学过程具有“可复制”性,为区域教学质量获得保障提供可能.有了“图”和“谱”,才能真正在目标体系层面上,系统地解决教、学和评的一致性.
(三)“图”与“谱”的关系
从有理数的“知识图”和“知识谱”可以看出它们之间具有如下关系:“图”宏观引领教学,可以使教学的整体结构清晰明了;“譜”精准分解教学目标,可以使教学靶向实施;“图”育“谱”,“谱”释“图”,“图”为纲,“谱”为目,纲举目张,方能有效地实现精准教学.
二、教好有理数的关键是教好负数概念和性质
有理数的概念教学就是围绕负数的引入,利用学生的生活经验,联系生活实际,聚焦具有相反意义的量,从理性具体(相反意义的量)中抽象出理性一般(正数和负数)的过程.引进一种新数(负数),还要研究新数的性质、新数的运算和运算律.
(一)概念教学
有理数概念教学的主要内容是有理数的概念、表示(符号表示和数轴表示)和分类(按定义分类和按符号分类).从具有相反意义的量到用数学符号表征,实质上是负数的构造过程.一般地,数(负数)的构造的基本方法是:尽量利用已有的符号(如已有的“+”“-”号在描述运算时,正好意义相反),通过意义建构,赋予新数具体而生动的含义,即把一个数看成是由符号和绝对值两部分构成.这为后面利用数轴研究有理数的性质创造了机会,也为归纳运算法则(先定号,后算值)奠定了基础.通过学习有理数的分类(整数和分数统称为有理数),掌握有理数的表示.由于整数可以理解为分母是1的分数[p1](p ∈ Z),分数可以表示为[pq][p,q∈Z,(p,q)=1,q≠0]的形式,因此可以这样理解:一切分数都是有理数,有理数可以用[pq]统一表示.这为学生将来判定一个数是无理数还是有理数提供了一个可以操作的判别准则[1].
(二)性质研究
借助数轴,让学生经历一次真正意义上的“数形结合”.把有理数和直线上的点对应,把研究数的性质转化为研究点的位置特征.两者能深度融合的基础是有理数的构成(正有理数、负有理数和零)和数轴的高度相似性(正方向、负方向和原点).其中数字“0”和“1”起关键作用,“0”是区别正有理数和负有理数的“基准”,“1”是有理数的单位.因此只要在直线上标定一个基准点O(原点),就把直线上的点划分成为两个部分,一部分的点和负有理数对应,另一部分的点和正有理数对应,区分正有理数和负有理数只需要规定一个正方向即可,这样便实现所有有理数和直线上的点对应.因此可以通过“翻译”数轴上点的位置特征得到有理数的性质:①点的顺序排列对应有理数的大小;②点分布的稠密对应有理数的稠密性(任意两个有理数之间还存在有理数).
数轴上一个点的位置由方向和距离决定,一个数由符号和绝对值决定.这为比较两个有理数的大小提供了操作规程:比较两个有理数的大小,可以先看符号,再比较绝对值的大小.首先确定0的基准作用,规定正数>0>负数;两个正数的大小即为绝对值的大小;比较两个有理数的大小,可以利用数轴的几何直观,确保有理数大小顺序和数轴上点的排列顺序一致,这样规定两个负数绝对值大的反而小就合情合理了.定义有理数的绝对值概念同时也解决直线上两点间距离的度量问题,为了度量的方便,需要规定一个“单位”,这便是数1的“单位”意义.绝对值概念也为后面学习有理数的运算奠定了基础.
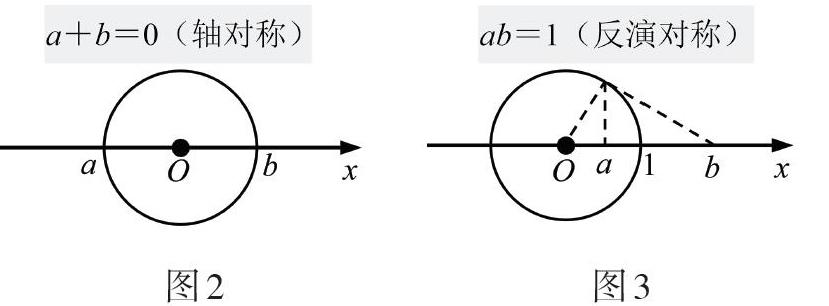
最后研究数轴上一些具有特殊位置关系的点,如位置关于原点对称的两个点,显然其绝对值相等,在数轴上具有明显的几何意义(图2).称这两个数(和为零)互为相反数,类比互为相反数,定义积为1的数互为倒数,这两个数也有很好的几何意义,便是反演对称(图3).
在有理数性质的学习过程中,学生体会什么是“数形结合”,经历研究一个陌生数学对象的基本方法.
三、教好有理数的运算关键在于运算的逻辑一致
代数的根本在于运算,研究有理数的概念和性质后,还需要研究有理数的运算.有理数的运算,归根结底是有负数参与的运算,但负数的运算对初中生而言是超越經验的,用任何具体例子来解释都有很大的局限性[2].
(一)用归纳的方法教有理数的运算和运算律是根本大法
在所有负数相关的运算中,负数和负数的乘法法则最为难以理解,教学时要注意到运算法则是人为规定的,但这种规定既要符合实际又要满足理论的相容性,初中阶段教学的主要任务是“使其相信”,要在运算法则的“承袭性”和逻辑的“自洽性”上下功夫.教好归纳就要设计合理的教学过程,通过过程中规律性的归纳,自然获得.
(二)教学流程再设计
先看看用数轴引入的设计方案:
例1 (环节A)小学已经学习“乘法是加法的简便运算”,如3×2=3+3=6.可以用如图5的数轴表示.
追问1:根据乘法和加法的关系,(-3)× 2=(-3)+(-3)=-6.用数轴如何表示这个关系?(如图6)
引导学生:① 画出图7;② 得到(-3)×2是3×2的相反数.
(环节B)教师小结并引导:改变相乘两数中的一个数的符号时,其积就变为原来积的相反数.同样,(-3)×(-2)是3×(-2)的相反数(如图7).获得负数×负数的运算律.
下面给出用归纳方法设计的教学流程:
(环节A):请你完成表2(阴影格为学生填写的数字),并说说理由.
师生活动后小结:①乘数逐次减小1,积逐次减小3. ②正数乘正数的积是正数,正数乘零等于零. ③正数乘负数的积是负数. ④积的绝对值等于各乘数绝对值的积.
追问:如果上述规律成立,那么表3中的空格应该如何填写?
师生活动后小结:①乘数逐次减小1,积逐次减小3. ②正数乘负数的积是负数. ③负数乘负数的积是正数,负数乘零等于零. ④积的绝对值等于各乘数绝对值的积.
归纳运算律要有意识地渗透运算程序,即先确定运算结果的“符号”,然后计算各因数绝对值的乘积.
(三)两种引入的优缺点
归纳获得的结论来自数学内部,设计好的问题使数学的内部规律外化为直观规律,符合学生的认知,容易被学生接受.利用数轴解释数字运算规律直观形象.归纳规律依赖问题设计和呈现方式,用表格形式呈现可能更有利于学生归纳得出运算规律.
利用数轴直观解释有后遗症.教学调研中发现一个看似“创新”的学生“研究”成果:(-3)×4=9.学生的解释:按照教师标在图上的箭头,(-3)×4就是把-3向右平移4个单位,此时箭头指向的位置恰好是9,所以(-3)×4=9.
原因就是这种直观缺乏数字运算背后的内在逻辑支持,学生纯粹从形的直观出发,用自己的方式理解,“生动形象”“自圆其说”地得到了一个“新”的规律.这是学习产生负迁移的结果.
(四)教好运算的关键是让学生学会优算
数学运算是演绎推理,数学运算主要表现为理解运算对象,掌握运算法则,探究运算思路,求得运算结果.使学生学会算得合理,算得准确.[□][◢]
参考文献:
[1]王红权.怎样教好无理数[J].数学通报,2018(6):18-22.
[2]章建跃.渗透数系扩充思想,加强运算能力培养(续)[J].中学数学教学参考,2012(9):6-8.

