端粒G-四链体结合酞菁分子的分子模拟研究

楼晓勤，黄依宁，许 奕，王梦露，李建峰，王志国

(杭州师范大学 医学部，浙江 杭州 311121)

0 引言

G-四链体(G4)作为一种核酸高级结构，通常形成于端粒末端DNA[1]、癌基因启动子[2]、非翻译mRNA[3]等G-碱基富集区。人端粒DNA末端有一段由[T2AG3]重复序列构成的长约100-200碱基的单链突出，该突出在生理条件下易折叠形成高稳定性的G4结构，从而抑制端粒酶延长端粒[4-7]。研究发现，约85%的癌症依赖端粒酶活性，而稳定G4能够抑制肿瘤的发生和发展[8,9]。因此，G-四链体稳定剂的开发成为癌症治疗领域关注的热点。

端粒G4在链取向、糖苷构象和末端延申序列等方面的差异导致了其构象的多样性，典型的G4结构呈现平行构象[10]、反平行构象[11]和杂合构象[12,13]。针对G4的结构特征，人们已经开发出一系列靶向性小分子稳定剂，包括黄连素[14]、咔唑[15]、卟啉[16]和喹啉[17]类化合物。这些化合物在结构上具有平面共轭性和正电性，使得它们能够通过π-π和静电相互作用与G4相结合。然而静电作用的特性决定了这些稳定剂不能有效区分G4和DNA双螺旋结构，使其在选择性上表现不佳，导致目前尚无靶向G4的癌症治疗药物得以应用。因此，选择性和特异性是目前G4稳定剂研究领域关注的焦点。

最近研究发现，负电性的四磺酸酞菁分子(anionic phthalocyanine 3,4′,4″,4‴-tetrasulfonic acid,APC)表现出良好的水溶性和端粒酶抑制活性，并且即使在过量双螺旋结构DNA存在的条件下APC仍表现出对端粒G4的高选择性[18]，而APC与最主要的端粒G4结构—平行构象G4[19]之间作用机制尚属未知。本文应用分子模拟方法确定了APC与平行构象G4的结合模式，通过主成分、非键相互作用和氢键分析解析了G4和APC复合物的构象变化特征，并进一步通过结合自由能计算和自由能分解确定了在二者结合中起关键作用的能量类型和关键碱基，从而在原子和分子水平上揭示了APC与平行构象端粒G4之间的作用机制。

1 方法

1.1 APC与端粒平行构象G4结构

APC结构(图1(a))由GaussView软件构建并应用密度泛函理论在B3LYP/6-31G(d)水平下进行构型优化，其原子电荷在HF/6-31G(d)水平下通过限制性静电势(RESP)计算得到[20]。分子动力学模拟中，APC分子的其它力场参数由AmberTools软件基于AMBER GAFF力场构建[21]。端粒平行构象G4结构由PDB数据库下载(PDB:1KF1)[10]并删除末端冗余核苷酸获得，如图1(b)，以使G4序列(5′-GGGTTAGGGTTAGGGTTAGGG-3′)[18]与实验报道一致。

1.2 分子对接

以达到动力学平衡状态的端粒平行构象G4结构为受体(图1(c)、(d))，以优化后的APC结构为配体，应用AutoDock 4.2.6软件[22]进行分子对接计算。对接计算应用Lamarck遗传算法，APC分子中所有可旋转键均设为柔性，一个包含100×100×100个格点、格点间距为0.375 Å的正方体盒子用于定义配体结合空间。对500次遗传计算的运行结果进行分组和比较，选取构象最多的两个组中结合能最负的构象作为APC的结合构象[20]。

1.3 分子动力学

应用AMBER 12软件[23]进行分子动力学模拟。将G4和G4-APC复合物分别置于尖端截断的八面体TIP3P水盒中心，设置其与水盒边界的距离为10.0 Å，在水环境中添加钾离子以使体系保持电中性。对G4应用FF99SB力场及parmbsc1和OL3+OL15矫正[24]，对环境和G4中的K+分别应用Amber标准参数(半径2.658 Å，井深0.00328 kJ·mol-1)和校正参数(半径1.705Å，井深0.1936829 kJ·mol-1)[25]。分子动力学模拟过程中，周期性边界条件、静电与范德华相互作用截断值、能量最小化、升温过程、温度与压力控制等参数设置均与文献报导一致[26]。

1.4 主成分分析

主成分分析(PCA)通过过滤模拟体系大量的局域性波动而揭示分子动力学中的本质运动[27]。应用交互式本质动力学方法(IED)[28]和AmberTools 的CPPTRAJ模块对所有G4-APC复合物中G4结构的骨架原子进行分析，以豪猪图方式显示前两个本征向量所代表的运动方式。

1.5 非共价键相互作用

应用NCIPLOT软件[29]计算APC与G4之间的非共价键相互作用，步长设为0.10。应用VMD软件[30]构建相互作用等值面，isovalue设为0.3 au。

1.6 结合自由能

分子力学/广义波恩表面积方法(MM/GBSA)[31]能够准确预测荷电分子的溶剂化自由能[32]，故应用此方法根据以下方程计算APC分子与端粒G4之间的结合自由能

ΔGbind=Gcomplex- (GG4+GAPC) ,

(1)

ΔGbind=ΔH-TΔS≈ ΔEMM+ΔGsolv-TΔS，

(2)

ΔEMM=ΔEint+ΔEele+ΔEvdW，

(3)

ΔGsolv=ΔGGB+ΔGSA，

(4)

其中EMM是气相状态下的相互作用能，包括内部应变能Eint(键，角和二面角能量)、静电相互作用能Eele和范德华(van der Waals,vdW)作用能EvdW。Gsolv为溶剂化自由能，包括极性项GGB和非极性项GSA。 应用单轨迹近似计算结合自由能时，ΔEint对结合自由能的贡献可忽略。应用广义波恩模型计算ΔGGB时，体系内部和外部介电常数分别设为4和80。应用LCPO算法[33]计算ΔGSA：ΔGSA=γΔSASA+β，其中γ和β分别设为0.0072 kcal·Å-2和0。应用AmberTools中的NMODE模块通过正则模式分析(NMA)计算熵变(TΔS)对结合自由能的贡献。从各G4-APC复合物最后40 ns分子动力学轨迹中平均提取500个结构用于计算ΔEele,ΔEvdW,ΔGGB和ΔGSA。由于NMA计算量较大，故从最后40 ns分子动力学轨迹中平均提取100个结构用于计算熵变。

2 结果与讨论

2.1 端粒G4与APC分子的结合模式

均方根偏差(RMSD)分析表明，平行构象端粒G4在200 ns时已达到平衡状态(图1(c))。三维构象比对发现，平衡状态G4相比晶体结构的构象差异主要位于loop区域(包括dT4dT5dA6,dT10dT11dA12和dT16dT17dA18)，参与形成G-四分体的鸟嘌呤则吻合较好(图1(d))。值得注意的是，晶体结构中位于顶层G-四分体外侧的K+离子在分子动力学模拟过程中自发逃逸到溶剂环境中(图1(b)、(d))，使顶层G-四分体暴露从而成为潜在的配体结合位点，此发现与文献报导一致。

以平衡状态G4作为受体结构的分子对接计算发现，APC分子主要以平行方式堆积于端粒G4顶层和底层G-四分体外侧(图2)。结合于顶层G-四分体时，APC共轭骨架与dG1,dG7,dG13和dG19形成π-π相互作用，磺酸官能团既与dG1，dA12和dA18形成阴离子-π相互作用又与dG19形成氢键相互作用O8(APCt)…H22-N2(dG19) (图2(a))。APC分子结合于底层G-四分体时，主要通过共轭骨架与dG3,dG9,dG15和dG21形成π-π相互作用，同时通过磺酸官能团与dG3,dG9和dG21形成氢键相互作用，即O7(APCb)…H22-N2(dG3),O10(APCb)…H22-N2(dG9)和O2(APCb)…H22-N2(dG21) (图2(b))。当两分子APC同时结合于端粒G4的顶层和底层G-四分体时，APC2t和APC2b与端粒G4的作用方式分别与APCt和APCb基本相同(图2(c))，表明已经结合的APC分子(APC2t)对第二个APC分子(APC2b)与端粒G4的结合影响甚微。

2.2 APC分子与端粒G4的结合特征

APCt分子的RMSD值在整个分子动力学过程中始终波动很小，显示其与端粒G4结合的稳定性(图3(a))。虽然端粒G4的RMSD值在130-140 ns时有较大波动，但在动力学模拟后期趋于稳定，表明G4结构达到平衡状态。均方根波动(RMSF)可以表征蛋白质或核酸等生物大分子中残基的柔性，分析发现APCt-G4体系中G4具有与晶体结构相似的RMSF变化趋势，即loop区域碱基的RMSF数值较高而参与构成G-四分体的鸟嘌呤呈现较低的RMSF值(图3(a))，表明G4结构的loop区域具有较大柔性而G-四分体则稳定性较高。结构比对显示，动力学平衡后APCt仍平行堆积于顶层G-四分体，此时G4与晶体结构在构象上的差异主要位于loop区域(图3(b))，与RMSF结果一致。主成分分析发现，前五个本征向量对APCt-G4体系中G4所有本质运动(由三十个本征向量近似表征)的贡献达59.13%(图3(c))，因此分子动力学过程中G4主要的本质运动方式可由前几个本质向量进行表征。豪猪图分析显示，第一本征向量主要表征了5′-端碱基向上的运动，第二本征向量主要表征了第一和第二loop结构的右向和左向运动(图3(c))。这两个本征向量所表征的运动趋势与结构比对的结果相一致(图3(b)、(d))。非共价键相互作用分析表明，平衡状态下APCt主要与端粒G4顶层G-四分体(包括dG1,dG7,dG13和dG19)形成范德华相互作用(图3(e))。分子对接中APCt通过磺酸官能团所形成的阴离子-π相互作用和分子间氢键相互作用由于稳定性差而消失。需要注意的是，APCt与dG1形成了一个新的分子间氢键O8(APCt)…HO5′-O5′(dG1)(图3(e))，有利于APCt与G4的稳定结合。

APCb分子和端粒G4在分子动力学过程中的RMSD波动均很小，显示二者结构的稳定性(图4(a))。APCb-G4体系中G4具有与晶体结构相似的RMSF变化趋势(图4(a))，表明分子动力学模拟的可靠性。与RMSD和RMSF结果一致，结构比对发现平衡状态下APCb仍平行堆积于底层G-四分体且G4与晶体结构的构象差异主要位于loop区域(图4(b))。APCb-G4体系中，前五个本征向量对G4本质运动的贡献为53.47%(图4(c))。豪猪图显示，第一本征向量主要表征了第二和第三loop的右向和左后向运动，第二本征向量主要表征了第二和第三loop的内向和外向运动(图4(c))。非共价键相互作用分析表明，平衡状态下APCb主要通过范德华相互作用结合于端粒G4底层G-四分体(包括dG3,dG9,dG15和dG21)外侧(图4(e))。APCb通过磺酸官能团与底层G-四分体碱基所形成的分子间氢键(图2(b))在分子动力学模拟过程中很快消失，显示出底层堆积结合模式下氢键相互作用的不稳定性。

图3 APCt与端粒G4的结合特征(a) RMSD和RMSF分析；(b) 结构比对,G4晶体结构以灰色飘带显示，APCt的对接构象以灰色棍状模型显示；(c) 主成分分析；(d) 豪猪图,暗红色和靛蓝色箭头分别表示第一和第二本征向量，箭头方向指示运动方向，箭头长度表示运动幅度；(e) 非共价键相互作用,绿色等值面表示范德华相互作用，蓝绿色等值面表示氢键相互作用

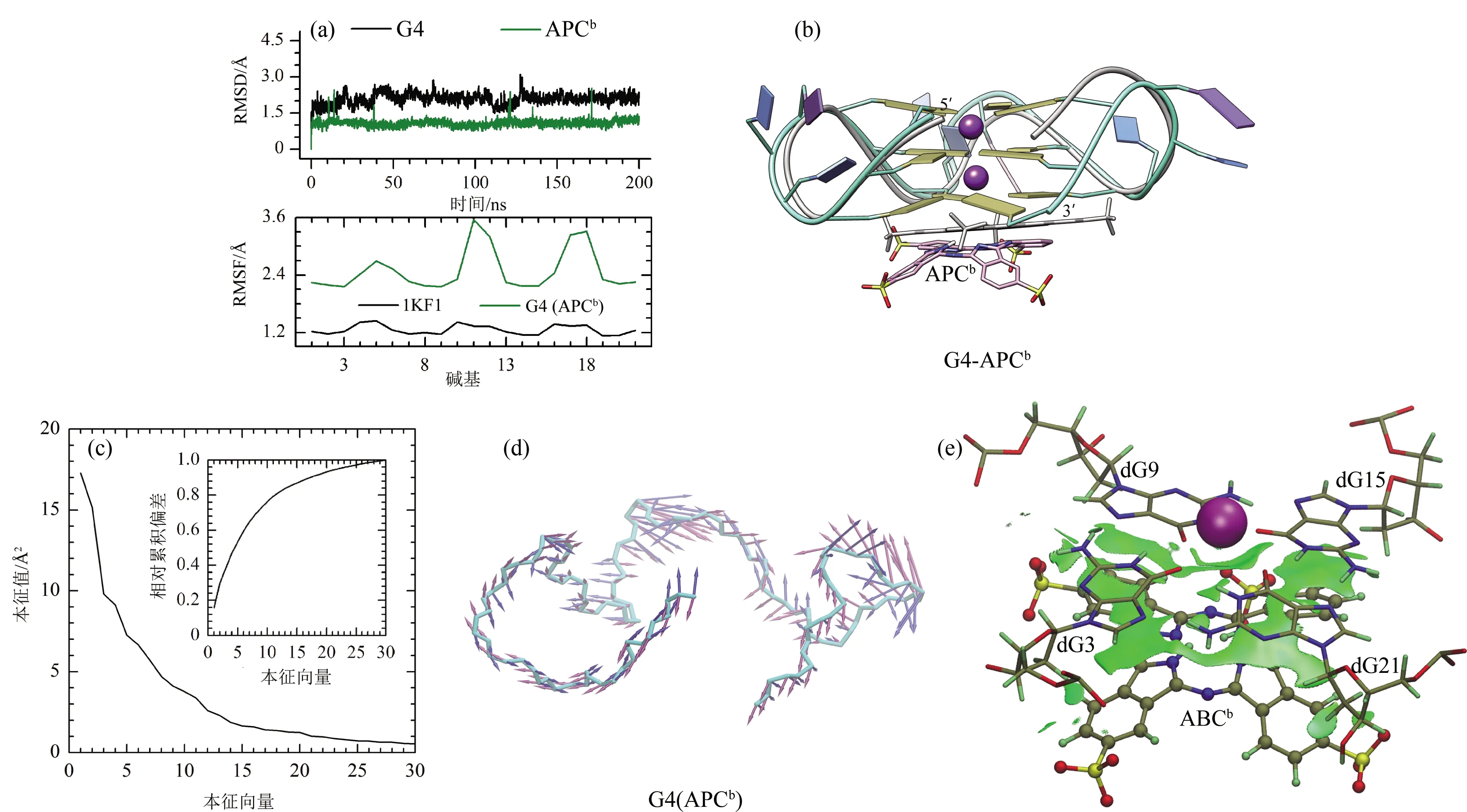
图4 APCb与端粒G4的结合特征(a) RMSD和RMSF分析；(b) 结构比对,G4晶体结构以灰色飘带显示，APCb的对接构象以灰色棍状模型显示；(c) 主成分分析；(d) 豪猪图,暗红色和靛蓝色箭头分别表示第一和第二本征向量，箭头方向指示运动方向，箭头长度表示运动幅度；(e) 非共价键相互作用,绿色等值面表示范德华相互作用，蓝绿色等值面表示氢键相互作用

双分子APC和端粒G4的RMSD波动均较小，表明它们所形成的三明治结构的稳定性(图5(a))。APC2-G4体系中G4同样呈现出loop碱基高RMSF值和G-四分体碱基低RMSF值的特性。与晶体结构的RMSF变化趋势相比，dA6和dA12的RMSF值明显偏高，表明双分子APC的结合使得dA6和dA12在结合复合物中的柔性增加(图5(a))。结构比对发现，APC2t和APC2b的平衡构象与对接构象重叠较好，而端粒G4与晶体结构的构象差异主要位于5-末端和loop区域(图5(b))。APC2-G4体系中，前五个本征向量对G4本质运动的贡献达61.59%(图5(c))。豪猪图显示，第一本征向量主要表征了第一loop结构的左向运动和5-末端的下向运动，第二本征向量主要表征了第一loop的上向运动和碱基dG7及dG8的下向运动(图5(d))。非共价键相互作用分析表明，平衡状态下APC2t和APC2b分别与端粒G4顶层和底层G-四分体形成广泛的范德华相互作用(图5(e)、(f))，以维持它们与端粒G4的稳定结合。此外，APC2t还同时与loop碱基dA12形成范德华相互作用以及与dG1形成分子间氢键相互作用O7(APC2t)…HO5′-O5′(dG1)，有利于进一步提升APC2t与端粒G4结合强度(图5(e))。

图6 分子间氢键的距离 (a) APCt与端粒G4碱基dG1间的氢键距离；(b) APC2t与端粒G4碱基dG1间的氢键距离

分子间氢键是配体与生物大分子之间重要的相互作用方式，是二者稳定结合的重要贡献因素[34]。由以上分析可知，只有堆积于顶层G-四分体外侧时APC分子才能与端粒G4结构形成分子间氢键。为了考察分子间氢键的稳定性，图6给出了分子动力学过程中氢键的距离变化。由图3(e)、图5(e)和图6可知，APCt和APC2t均可通过相同的磺酸基O原子与端粒G4中dG1碱基的羟基H原子形成氢键。由于连接磺酸基与APC骨架的C-S单键可自由旋转，使得磺酸基中三个O原子(O7,O8和O9)与dG1羟基H原子的平均距离均约为3.06 Å。同时，该磺酸基中每个O原子参与的分子间氢键的持续时间均约占分子动力学模拟总时间的32.67%，这意味着在超过98%的动力学模拟时间里APC分子和dG1碱基间均存在氢键相互作用，表明分子间氢键相互作用的稳定性。

表1 平行构象端粒G-四链体的Hoogsteen氢键特征

2.3 APC分子对端粒G4结构的稳定作用

Hoogsteen分子内氢键O6…H1-N1和N7…H21-N2是维持G-四分体平面结构稳定的关键作用力，其状态可用以表征G4结构的稳定性[26]。表1列出了结合APC分子前后端粒G4各G-四分体中的Hoogsteen氢键参数，可以发现所有氢键在整个分子动力学过程中的平均时长均高于94.27%，表明端粒G4结构的稳定性。APCt分子的结合将顶层G-四分体O6…H1-N1和N7…H21-N2的平均时长分别从未结合时的94.47%和94.67%提升到99.89%和99.66%，APCb分子则将底层G-四分体O6…H1-N1和N7…H21-N2的平均时长分别由99.15%和99.56%提升到99.74%和99.81%，表明APC分子提升了其所结合区域的稳定性。双分子APC的结合则将端粒G4所有G-四分体O6…H1-N1和N7…H21-N2的平均时长提升至99.45%和99.68%以上，同时将Hoogsteen氢键时长的最小值由未结合状态的89.28%提升至95.23%，从而从整体上提高了端粒G4结构的稳定性。

结合自由能可用以评估配体分子与蛋白质或核酸等生物大分子之间的亲和能力[31]。表2列出了应用MM/GBSA方法计算得到的APC分子与端粒G4之间的结合自由能，可以发现负电性APC分子与端粒G4负电性磷酸骨架之间的静电排斥作用使得静电相互作用不利于二者的结合。同时，APC分子与端粒G4的结合是一个体系自由度减少的过程，因此熵变是对结合自由能的不利贡献。极性和非极性溶剂化作用以及范德华相互作用是APC分子与端粒G4稳定结合的主要贡献者，其中极性和非极性溶剂化能恰能大致抵消静电作用能对结合的不利贡献，而熵变对结合自由能的贡献又大致相同，这就使得范德华作用能的大小实质上决定了APC分子与端粒G4亲和力的强弱(表2)。

比较不同结合模式下结合自由能的大小可知，当APC分子以1:1和2:1比例与端粒G4结合时均是堆积于顶层G-四分体外侧的结合方式(APCt和APC2t)在能量上更为有利(表2)，这和非共价键相互作用和分子间氢键的分析结果一致。同时，在以2:1比例结合时APC2t和APC2b均较1:1比例结合时的APCt和APCb在能量上更为有利，表明第二个APC分子的结合不仅能更全面的提升端粒G4的稳定性(表1)，同时也提升了两个APC分子各自与端粒G4的亲和力(表2)。

表2 平行构象端粒G-四链体与APC分子的结合自由能

图7 基于碱基的结合能分解

进一步的结合能分解分析发现，构成顶层G-四分体的碱基dG1,dG7,dG13和dG19对APCt和APC2t与端粒G4的结合贡献最大，而构成底层G-四分体的碱基dG3,dG9,dG15和dG21对APCb和APC2b与端粒G4的结合贡献最大(图7)。需要注意的是，碱基dA12对APC2t的结合也有重要贡献(-1.29 kcal·mol-1)，但是其对APCt的结合则贡献微弱(-0.18 kcal·mol-1)(图7)，这也是与端粒G4结合时APC2t较APCt亲和力更强的重要原因之一。结合能分解与非共价键相互作用分析的结果完全一致，进一步增强了当前研究结果的可靠性。

2 结论

本文应用分子对接和分子动力学方法对具备高选择性的负电性APC分子与人端粒平行构象G4的作用机制进行了系统研究。研究发现，APC分子倾向于以平行堆积的方式结合于端粒G4顶层和底层G-四分体平面的外侧。相比底层堆积的结合方式，APC分子结合于顶层G-四分体时除可以形成广泛的范德华相互作用外，还能够与dG1碱基形成稳定的分子间氢键相互作用，使得顶层堆积的结合方式在能量上更为有利。APC分子以2:1比例结合时能够更全面的提升端粒G4结构的稳定性，并且每个APC分子与端粒G4的亲和力均较单独结合时更强。结合自由能计算表明静电相互作用不利于APC分子与端粒G4的结合，而范德华作用能作为二者结合的重要贡献因素，在本质上决定了APC分子在不同结合位点亲和力的强弱。这些发现在原子和分子水平上揭示了APC分子与端粒平行构象G4的作用机制，对新型特异性端粒G-四链体稳定剂的开发具有重要意义。