数学语言转换在概念学习中的应用
李琨璇 张文俊


【摘要】数学语言是数学内容的载体,是传达数学知识的重要方式.数学语言的转换包括自然语言与数学语言之间的转换和数学语言内部的转换.本文结合具体教学实例,引导学生在学习数学概念时,通过数学语言转换感知概念外形,获得概念意象,总结概念定义,强化概念本质,最终灵活掌握概念.
【关键词】数学语言;概念学习;数学语言转换
斯托利亚尔提出,“数学教学就是数学语言的教学”.从这个意义上来说,数学语言对于数学学科和数学教学来说具有重要的意义.数学语言的表现形式有三种,分别是文字语言、符号语言和图形语言.其中,文字语言在数学概念、性质和定理方面多有应用,图形语言直观清晰,符号语言虽简明但不易于理解.因此,在教学过程中,当学生不理解某个概念或题目时,教师可借助数学语言之间的相互转换来帮助学生理解并掌握数学知识.
恩格斯也曾说: “在一定意义上,科学的内容就是概念的体系.”数学概念是数学知识的基本组成单元,是数学知识系统的内核源泉,也是学生进行思维活动的基础,它反映了数学对象的本质属性,因此数学概念的获得与理解具有一定的抽象性.若学生对于数学概念的学习只停留在记忆层次,将会影响其对数学概念的理解与应用.因此,在概念教学时,教师可通过数学语言转换,降低学生的学习难度,带领学生经历数学概念的形成过程,把握概念的本质属性,使学生真正理解并掌握概念,提升数学学习的效率.
一、数学语言转换含义
(一)什么是数学语言转换
弗赖登塔尔曾提出“学生必须学会将一种语言翻译成另一种语言”.这里的“翻译”即指数学语言的转换,在保持数学对象本质属性不变的前提下改变语言的外在表现形式,包括自然语言与数学语言之间的转换,不同形式的数学语言转换以及同种数学语言内部的不同表征形式的转换等.
(二)数学语言转换的类型及其内涵
1.自然语言与数学语言的外部转换
生活中常用的语言就是自然语言,对小学生来说,用自然语言来描述数学中的事物与情境更容易让他们接受与理解,但自然语言不符合数学的简洁性和精确性,因此用自然语言表达数学事实时,必须改造它,使之适应数学的需要.
一方面,自然语言转换为数学语言,是将一般问题转化为数学问题,在数学学习中体现为将情境中的数学信息提取出来,表述成数学问题再解决.因此,自然语言转换为数学语言是一个“数学化”的过程.
另一方面,数学语言转换为自然语言,是让学生用自己的语言表述出数学中的定义、定理等内容,当学生能够清晰地表达自己的想法时就表明他们对此已有深刻的理解.因此,为使学生对数学知识的理解更透彻,需要将数学语言“通俗化”,轉换为他们更熟悉、亲切的自然语言.
2.数学语言的内部转换
数学语言内部的转换是指不同形式数学语言之间的转换和相同形式数学语言之内的转换.
(1)不同数学语言形式之间的相互转换
在进行数学理解时,需要数学语言内部不同形式的转换,例如,将文字语言转换为图形语言,用形象直观的图形帮助学生进行理解,再将图形语言转换为符号语言进行计算等;进行数学表达时,把求得的结果或得到的结论转换成所要求的表现形式,因此很多数学活动其本质都可以理解为数学语言转换的过程.
(2)相同数学语言形式之内的相互转换
卢清荣认为“数学语言转换是数学思维不断发展的过程”.相同数学语言形式之内的转换更为明显,例如,在学习面积单位之间的进率关系时,为探究平方分米与平方厘米的关系,北师大版教材提出了以下方法:
由长度单位之间的关系来推导面积单位之间的关系,经历从符号语言到符号语言的转换,可以发展学生的逻辑推理能力;对同一个知识从不同的角度来表示,可以让学生体会知识之间的联系,并在不断思考中促进思维的发展.
二、数学语言转换与数学概念学习
(一)概念习得
现代认知心理学认为学生学习数学概念的方式有两种,分别是概念形成和概念同化.概念形成是指从具体实例或者模型出发,发现事物的共同属性,抽象出事物的本质特征,归纳形成新的概念.概念同化是指学习新概念时以原有的数学认识结构为依据,将新知识进行加工,如果新知识与原有认知结构中适当的概念有联系,那么通过新旧概念之间的相互作用,将新概念纳入原有认知结构中,使原有认知结构得到改组或扩大,这一过程称为概念同化.
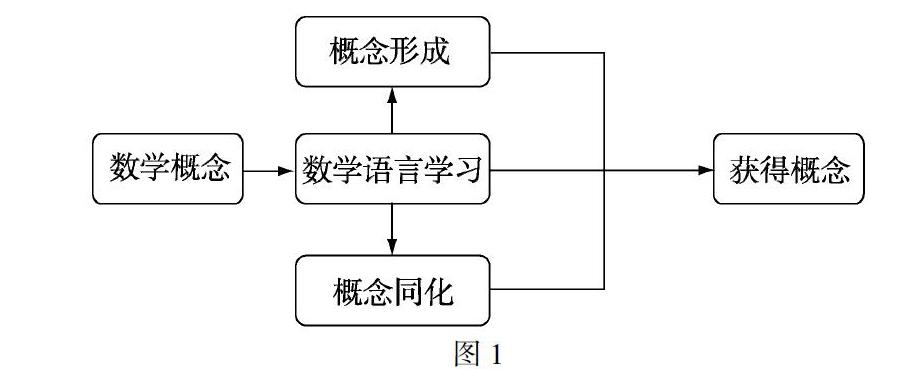
那么,除此之外,是否还有其他的方式获得数学概念呢?答案是肯定的,喻平教授认为数学语言学习也是数学概念获得的一种方式,例如:行列式、矩阵等概念的学习是直接以数学语言学习获得的.因此,数学语言的学习是一种有意义的学习,它表现在概念形成和概念同化的每一阶段,只有当学生对数学文字、符号都有了实质性的理解,才可能从本质上获得概念.因此数学概念的习得可总结如下(如图1):
(二)数学语言转换在概念学习中的作用
下面以“分一分”这节课为例来谈谈在概念形成过程中数学语言转换如何帮助学生理解并掌握概念.
1.自然语言转换为数学语言,感知概念外形
师:把四个苹果分给两名同学,保持公平公正,该怎么分?每名同学分几个?
师:把两个苹果分给两名同学,保持公平公正,该怎么分?每名同学分几个?
首先由现实问题引入,经过两次分苹果,使学生了解每名同学分得“一样多”,用数学语言表示就是“平均分”.将自然语言转换为数学文字语言,使用并提出下面问题,让学生感受数学语言的概括性和精确性.
师:把一个苹果平均分给两名同学,每名同学得几个?
再一次分苹果,学生发现“半个”已不能用学过的数字符号来表示,教师鼓励学生发挥想象力,大胆创造表示“一半”的方法,可以画各种各样的图形,也可以发明一种符号.有学生画出各种图形的一半来表示,也有学生提出用符号语言12表示,在转换后多种形式的数学语言对比中,让学生感受用符号语言“12”表示“一半”的简洁性和优越性,体会学习分数的必要性.
2.符号语言与图形语言相互转换,获得概念意象
教师鼓励学生说说看:“刚才是怎么得到12的?”教师接着通过下面涂一涂的方式,在学生头脑中展现图形语言向符号语言转换的过程.
分别涂出下列图形的12.
涂出每个图形的12,就是涂出它的一半,在直观的图形中可以轻而易举地表示出来.因此符号语言到文字语言,再到图形语言转换的过程,能帮助学生建立数量符号12和相对应图形之间的联系.同时,在此过程中教师可引导学生抛弃形状、大小、颜色等无关因素,体会部分与整体之间的联系,感受分数概念的本质特征——把一个整体平均分成两份,其中的一份就是12.
最后教师引导学生模仿分数12的学习过程,用折纸、画图的方法“创造”其他分数,学生再次经历图形语言和符号语言的相互转换,在头脑中形成了一定的概念意象,为掌握和理解分数的外延和内涵奠定了基础.
3.图形语言转换为文字语言,总结概念定义
归纳总结:12,14,38,45都是分数.
教师要以小学生认知结构为基础,选取具有代表性的特例,帮助学生建立感知的概念表象,认识分数的读法、写法以及各部分名称,此时学生掌握了概念的外延.
教师在讲解14各部分表示的含义时,可以让学生想象,分母4表示把一张纸平均分成4份,分子1表示其中的1份,再结合多个具体的分数描述帮助学生进一步理解分数表示部分与整体之间的关系,进而总结出分数的定义性概念:把一个整体平均分成若干份,表示这样的一份或几份的数叫作分数.因此,图形语言转换为文字语言有助于帮助学生对概念内涵的理解由感性认识上升为理性认识.
4.判断正反例,强化概念本质
下面哪些图形的涂色部分是它的14,在括号里画“”.
判断分数表示阴影部分是否正确是图形语言转换为符号语言的过程,可以从正、反两方面对分数的意义进行概念的辨析:先根据图形判断其能否用所給的符号语言来表示,若能,则正确;若不能,则接着剖析反例中错误的原因.根据符号语言(所给分数)把所给图形语言转换为正确的图形语言.最后用文字语言结合符号语言固化自己对分数的认识,进一步抽象出分数概念的特征——把一个整体平均分才能用分数表示.学生经历多次数学语言的“逗留”,对分数的意义逐步清晰,教师结合正例和反例引导学生灵活转换数学语言,使其更好地掌握概念.
总之,教师引导学生经历分数概念形成的过程就是数学语言不断转换、不断应用和不断内化的过程,学生能通过数学语言转换,概括出分数概念的外延和内涵,深刻理解概念的本质属性,逐步形成概念域和概念系,从而完善其认知结构.
【参考文献】[1]斯托利亚尔.数学教育学[M].北京:人民教育出版社,1984.
[2]赵文静.数学学习中的数学语言转换[J].数学之友,2014(16):44-46,48.
[3]喻平.数学教学心理学[M].北京:北京师范大学出版社,2018.
[4]喻平.数学概念学习刍议[J].课程·教材·教法,1995(4):31.
[5]吴正宪,刘劲苓,刘克臣.小学数学教学基本概念解读[M].北京:教育科学出版社,2014.

