APOS理论视角下函数在一点连续的概念教学研究
林欢玲


【摘要】本文为研究函数在一点连续的概念教学,在APOS理论的视角下,经过一系列内化、压缩、解压缩的心理机制,建立 “函数在某一点的连续性”的三个等价定义的图式,形成概念域.
【关键词】APOS理论;连续性
一、引 言
函数的连续性是函数的一个最基本的概念,是运用极限方法对连续性现象进行研究,而函数在一点的连续性的三种定义的关系是认知连续性概念的思维障碍点.杜宾斯基提出APOS理论,主要应用于概念教学,注重概念的形成与学生思维建构的过程.因此,本文以APOS理论为基础,教师要能够有针对性地为“函数在一点的连续性”的教学方案提供依据,帮助学生克服对连续性概念的认知障碍.
二、相关概念
(一)函数在一点连续的定义
在连续函数的概念中,对于函数在一点的连续性,有下面三种常见的定义方式:
定义1 设函数f(x)在某U(x0)上有定义,若limx→x0f(x)=f(x0),则称f(x)在点x0连续.
定义2 设函数f(x)在某邻域U(x0)上有定义,记Δx=x-x0,Δy=f(x)-f(x0)=f(x0+Δx)-f(x0),有limΔx→0Δy=0,则称f(x)在点x0连续.
定义3 设函数f(x)在某邻域U(x0)上有定义,若对任意的ε>0,存在δ>0,使得当|x-x0|<δ时有,都有|f(x)-f(x0)|<ε,則称f(x)在点x0连续.
(二)APOS理论
杜宾斯基以皮亚杰提出的建构主义为基础,提出了数学概念学习的APOS理论模型.该理论模型认为学生学习数学概念是要进行心理建构的,此建构过程要经历以下四个阶段:活动、过程、对象、图式.其中,“活动”是个体通过一步一步的外显性(或记忆性)指定去变换一个客观的数学对象.当“活动”经过多次重复而被个体熟悉后,就可被内化为一种称之为“程序”的心理操作.当个体能把“程序”作为整体进行操作时,这一程序就变成了一种心理“对象”.一个数学概念的“图式”是指相应的“活动”“程序”“对象”以及与某些一般原理相联系的其他“图式”所形成的一种个体头脑中的认知框架,可以用于解决与这个概念相关的问题.“活动”“过程”“对象”也可看作数学知识的三种状态,“图式”是由这三种知识结构构成的一种认知结构.
三、APOS理论视角下函数在一点连续的概念的教学研究
(一)运用APOS理论的可行性分析
学生对于“连续性”的初始概念图像,是坐标平面上一条连绵不断的曲线,而不是在一点上具有连续性,故而函数在一点的连续性与学生所认知的连续性的概念形象就产生了认知冲突,可能导致学习障碍.内化与压缩作为APOS理论的重要心理机制,可以对函数在一点连续性的学习障碍提供解释与解答.教师可利用APOS理论,在过程阶段与对象阶段,结合函数极限构造函数在一点连续的概念图像,将极限概念过渡到连续性概念,帮助学生克服函数在一点连续性的学习困难,从而形成对函数在一点连续的真正理解.
对于函数在一点连续的三个等价定义,在教材安排上,不同版本的教材采用的编排顺序不同,但都是在学习函数极限之后,采用上述定义中的某个定义引入连续性概念,进而将另外两个定义作为等价定义给出.因此,在认知层面上,对上述三种定义的教学,要把握极限理论中极限概念和连续性概念的联系.选取不同的定义引入连续性概念,会影响初学者对该概念的理解以及所出现的学习障碍.
(二)APOS视角下函数在一点连续的概念的教学研究
从几何直观上看,连续函数是坐标平面上一条连绵不断的曲线,故学生对连续性并非完全陌生的,将学生所认知的自然界的连续变化反映在数学上,就是量的变化,而反映这种连续变化现象的数量关系就是函数的连续性.连续函数的概念是“隐性”的,需要通过外显的活动,将连续性呈现出来,由此获得连续函数概念的“表象”.
(三)关于三个定义的教学研究
1.定义1的教学研究
问题1:分别画出①f(x)=x,②f(x)=1x,③f(x)=x+2(x≥0),x-2(x<0)的图像,并思考下述问题:(1)图像是否连续?若是不连续,又在哪里间断?图像断开的原因是什么?(2)当x→0时,函数极限值分别是多少?
通过解答(1),学生单个地分析函数是否连续以及图像断开的原因,将这个过程经过多次重复后,学生能通过对比①②③发现x=0是②③是否连续的关键点.解答(2)时,当图像出现间断,学生不得不运用函数左、右极限进行计算.学生通过计算,便会猜想当x趋于0时的函数极限、函数在x=0处的函数值与函数的图像连续存在联系.这种思考过程即心理机制上的内化,进而达到“程序”阶段.
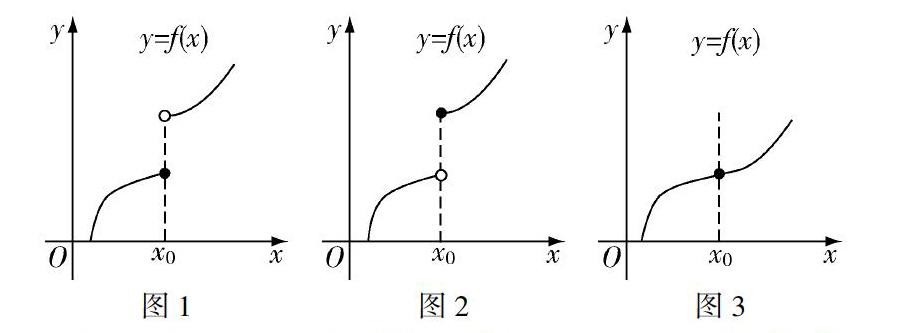
问题2:接下来脱离具体情境,将x=0拓展到x=x0的情况,将情境中的函数图像归纳为下述情况,如图1,图2,图3所示,继续思考上述问题.
教师引导学生思考:若是函数在点x0处出现间断,依照问题1的思考过程,借助图像,运用左、右极限的知识加以理解.对于图1,函数在点x0处出现间断,对于函数曲线上断开的点f(x0)可归为左侧图像,那么,函数在点x0处的左极限恰好等于这一点的函数值f(x0),即limx→x-0f(x)=f(x0).对于图2,函数曲线上断开的点f(x0)可归为右侧图像,那么,函数在点x0处的右极限恰好等于这一点的函数值f(x0),即limx→x+0f(x)=f(x0).对于图3,函数在点x0处没出现间断,那么这点不仅可以归为左侧图像,也可以归为右侧图像,由左右极限的定义,可得limx→x0f(x)=f(x0).
教师要让学生意识到:曲线在某一点连续与不连续的差别,在于曲线在该点处的函数值是否产生了“突变”,并且发现函数在点x0连续应满足三个条件:函数f(x)在某邻域U(x0)上有定义;极限limx→x0f(x)存在;极限limx→x0f(x)的值等于点x0处的函数值f(x0).此时,上述“程序”就已经被“压缩”为一种“对象”.
最后,教師引出函数在点x0处连续的定义为:设函数f(x)在某邻域U(x0)上有定义,若limx→x0f(x)=f(x0),则称f(x)在点x0连续.
完成这个过程,APOS理论视域下,函数在一点连续的定义与函数极限的联系,是之前所习得的函数极限图式的进一步发展,形成函数连续性概念的新图式.
2.定义3的教学研究
问题3:由于函数在一点的连续性是通过极限定义的,所以可类比函数极限的定义,试着用ε-δ语言叙述定义1.
学生思考:类比函数极限的定义,可由定义1得到其ε-δ语言,如表1所示:
教师细致分析,让学生领会:讨论极限时,假定f(x)在点x0某空心邻域U。(x0)上有定义(f(x)在点x0可以没有定义),而“函数f(x)在点x0连续”,则要求f(x)在某邻域U(x0)上有定义.此时,对于|f(x)-f(x0)|<ε,当x=x0时总是成立的,所以在极限定义中的“0<|x-x0|<δ”换成了在连续定义中的“|x-x0|<δ”.
最后教师总结定义:设函数f(x)在某邻域U(x0)上有定义,若对任意的ε>0,存在δ>0,使得当|x-x0|<δ时,都有|f(x)-f(x0)|<ε,则称f(x)在点x0连续.
这样,围绕limx→x0f(x)=f(x0)这个“对象”,定义1与定义3建立等价关系.
3.定义2的教学研究
对于定义2,教师可通过几何知识更为直观地进行教学.为理解“函数y=f(x)在点x0连续”的概念,教师引入增量的概念,记Δx=x-x0,称为自变量x(在点x0)的增量或改变量.设y0=f(x0),相应的函数y(在点x0)的增量记为Δy=f(x)-f(x0)=f(x0+Δx)-f(x0)=y-y0.其中,自变量的增量Δx或函数的增量Δy为实数.
问题4:引进了增量的概念之后,固定点x0,反复变化下图中Δx的大小,观察其对应的Δy如何变化.
教师引导学生理解自变量的增量Δx或函数的增量Δy可以为正数、0或者负数.当Δx>0时,自变量x增大,函数的增量Δy>0,反之,当Δx<0时,自变量x减小,函数的增量Δy<0.
在“活动”阶段,学生依次对h(x)和f(x)的图像实施Δx的变化,以观察其对应的Δy的变化.重复多次“活动”后,慢慢就内化为“程序”,学生能对比发现图4的函数y=h(x)的图像在点x0处间断,保持x0不变,当Δx趋近于0时,点N沿曲线趋近于点N′,此时Δy为定值,在点x0处不连续.图5的函数y=f(x)的图像是一条连续变化的曲线,令f(x0)=M,f(x0+Δx)=N,保持x0不变,当Δx趋近于0时,点N沿曲线趋近于点M,Δy趋近于0.学生对整个区间上函数值的增量随自变量的增量变化趋势有整体认识,上述“程序”就被“压缩”成一种“对象”.
最后,教师总结得到定义2:设函数f(x)在某邻域U(x0)上有定义,记Δx=x-x0,Δy=f(x)-f(x0)=f(x0+Δx)-f(x0),有limΔx→0Δy=0,则称f(x)在点x0连续.
此时,学生对“函数在一点连续”的三个定义有了完整的形式化表述,但对三个定义的等价关系的认识还处于分离的状态,所以,认识需要上升到“图式”阶段.教师要引导学生对定义2进行“解压缩”,在定义2中,令Δx=x-x0,则Δy=f(x)-f(x0)=f(x0+Δx)-f(x0),当Δx→0时,有x→x0,Δy→0,则[f(x0+Δx)-f(x0)]→0,即f(x)→f(x0),可得limx→x0f(x)=f(x0).该过程围绕“limx→x0f(x)=f(x0)”,定义1与定义2建立等价关系.
四、总 结
对于“函数在某一点的连续性”的三个等价定义的教学,教师应引导学生主动建构,把握学生对概念的思维障碍点,避免让学生死记数学概念,而无法理解“函数在某一点的连续性”的三个等价定义之间的关系.
【参考文献】[1]李士锜.数学教育心理[M].上海:华东师范大学出版社,2001.
[2]华东师范大学数学系.数学分析(第四版)[M].北京:高等教育出版社,2010.
[3]鲍建生,周超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009.
[4]罗新兵,罗增儒.数学概念表征的初步研究[J].数学教育学报,2003(02):21-23.
[5]Ed Dubinsky,Kirk Weller,Michael A.Mcdonald,Anne Brown.Some Historical Issues and Paradoxes Regarding the Concept of Infinity: An Apos-Based Analysis: Part 1[J].Educational Studies in Mathematics,2005(3):335-359.
[6]D Tall,S Vinner.Concept Image and Concept Definition in Mathematics with Particular Reference to Limits and Continuity[J].Kluwer Academic Publishers,1981(2):151-169.

