机械轴与虚拟轴复合的磁流变抛光
张 韬,何建国,黄 文,樊 炜,张云飞
(中国工程物理研究院机械制造工艺研究所,四川绵阳621900)
1 引 言
随着现代科学技术的不断发展,复杂曲面光学元件在科学实验和国防领域中的应用越来越广泛。面向科学实验和国防科技的光学产品和装置对复杂曲面光学元件的需求与日俱增[1],大量高精度曲面镜被用来校正像差、改善像质、扩大视场、简化结构与减轻质量,以促进光学系统的性能提升。磁流变抛光技术可以实现光学元件的快速高精度低成本制造,因而在光学加工中应用广泛。为实现材料的确定性去除,需要实时保证抛光轮适应工件的面形,保持法向接触以保证去除函数的一致[2]。在加工曲面面形时,常规的方法是通过机床的机械轴联动控制工件的位姿和位置实现工具上的定点与工件法向接触。对于非球面和自由曲面抛光,机床需要更多的转动轴来保证加工自由度,而多自由度的机床造价昂贵、占用空间较大、结构复杂,实现高精度联动控制难度较大;其次,加工能力受限于机床转动轴的行程,当元件陡度较大时会出现超行程的问题;此外,机械轴本身的质量和惯量很大,在加工高陡度曲面元件时会接近其极限行程,运动产生的机构振动和定位误差大,导致面形精度恶化,影响加工质量[3]。由此可见,低自由度下曲面元件的加工和联动机械轴加工行程的扩大,对于提高磁流变抛光工艺的适用性有着重要的意义。
机床自由度是由机械轴数量决定的,因此在低自由度下加工曲面件本质上是降低对机械轴数量的要求。针对这个问题,周洁[4-5]在利用七轴四联动砂轮工具磨削自由曲面时设计了一种母线圆弧面结构的砂轮,整个外缘圆角作为工作表面,找到能和自由曲面法向量一致的磨削点来拟合,使得四轴联动机床上加工扭转叶片成为可能。在磁流变抛光工艺中,美国QED公司的Maloney等[6]提出了“虚拟轴”代替机床联动轴,以解决磁流变机床自由度不足的问题。磁流变抛光的工具是抛光轮,与文献[4]砂轮外缘一样有圆弧部分。该方法同样利用了圆弧的几何对称性,抛光时工件与抛光轮上缎带的法向接触点根据面形法矢在一定范围内变动,因此不需要添加物理轴,同时QED公司抛光轮上的触点可变范围达±45°。国防科技大学的宋辞[8]等人根据抛光轮和磁铁的结构尺寸以及工艺参数理论计算了可加工工件的最大斜率,并进行了磁场稳定性仿真和测量。该方法以去除函数的体去除率和形态作为衡量指标,确定了±7°的最大可加工工件倾角。虽然去除函数特性非常稳定,但是工件可加工倾角范围太小,导致虚拟轴的范围受限。中科院长春光机所的李龙响[9]提出虚拟轴可用的前提是抛光液循环系统和永磁场的分布稳定,并进行了稳定永磁场的设计,结合去除函数完整性和实际加工需求给出了±15°的工件倾角范围,以体去除率证明去除函数的稳定性,并给出了虚拟轴下位姿控制坐标的变换关系。
综合目前的研究来看,低自由度下加工陡度较低曲面的问题已通过虚拟轴解决,但针对高陡度曲面元件的加工,虚拟轴却难以满足要求,此时依然需要单独调用机械轴联动参与加工过程。目前,没有学者提出将虚拟轴和机械轴复合使用的方法用于磁流变抛光,因此虚拟轴的适用性还有进一步扩展的潜力。本文针对高陡度曲面元件加工时机床联动轴行程不足的问题,结合磁流变抛光中的虚拟轴原理,提出了将虚拟轴和联动轴结合以间接扩展机械轴行程的方法,并以此为基础进行了该方法的坐标解算。实验表明,本文所提出的磁流变加工方法在提高机床联动轴加工行程的同时保证了面形收敛,机床的加工能力得到了明显的提升。
2 磁流变抛光及虚拟轴原理
磁流变抛光的基本原理是磁流变液(由磁性颗粒、抛光粉、基液和稳定剂组成)通过具有传送和回收功能的循环系统流动,从而实现对工件表面的加工。其中,抛光液通过输液泵由喷嘴喷洒在旋转的抛光轮上,在高梯度磁场的作用下凝聚变硬,成为具有黏塑性的Bingham介质缎带,在工件与缎带接触区以剪切的形式实现对材料的去除,如图1所示。
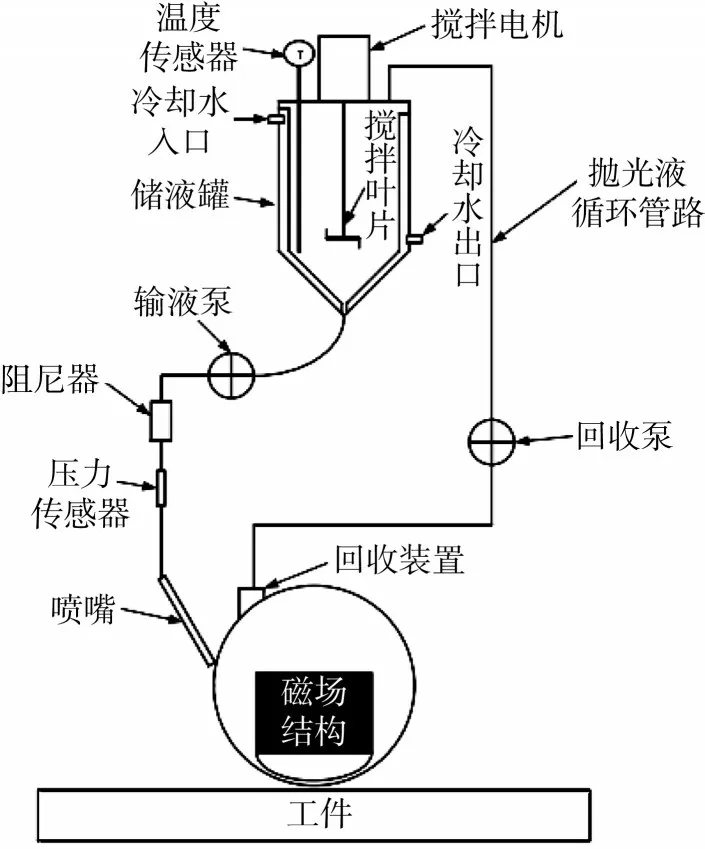
图1 磁流变抛光循环系统Fig.1 Magnetorheological finishing circulation system
当前的磁流变抛光技术与数控加工技术相结合,形成了数控磁流变抛光技术,这是一种基于计算机控制表面成形技术的确定性抛光工艺[10]。数控磁流变抛光的基本原理是根据干涉仪等测量仪器获得工件的面形数据,确定材料去除量,根据去除函数特性生成抛光头的运动轨迹和驻留时间,利用计算机控制远小于工件口径的抛光磨头(磁流变抛光中为抛光轮下的缎带)沿着规划的路径和驻留时间在工件表面运动,保持磨头与工件间的相对线速度和正压力一定,去除函数保持确定的特性,经过多次的迭代实现面形误差的定量去除。加工过程就是抛光工具的去除函数与单位面积的驻留时间在工件表面的卷积,可表示为:
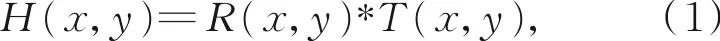
其中:H(x,y)是驻留点位置(x,y)处的材料去除量,R(x,y)是去除函数在(x,y)处单位时间的材料去除量,T(x,y)是(x,y)处单位面积的驻留时间。可见,确定性修形的关键因素在于去除函数的稳定。
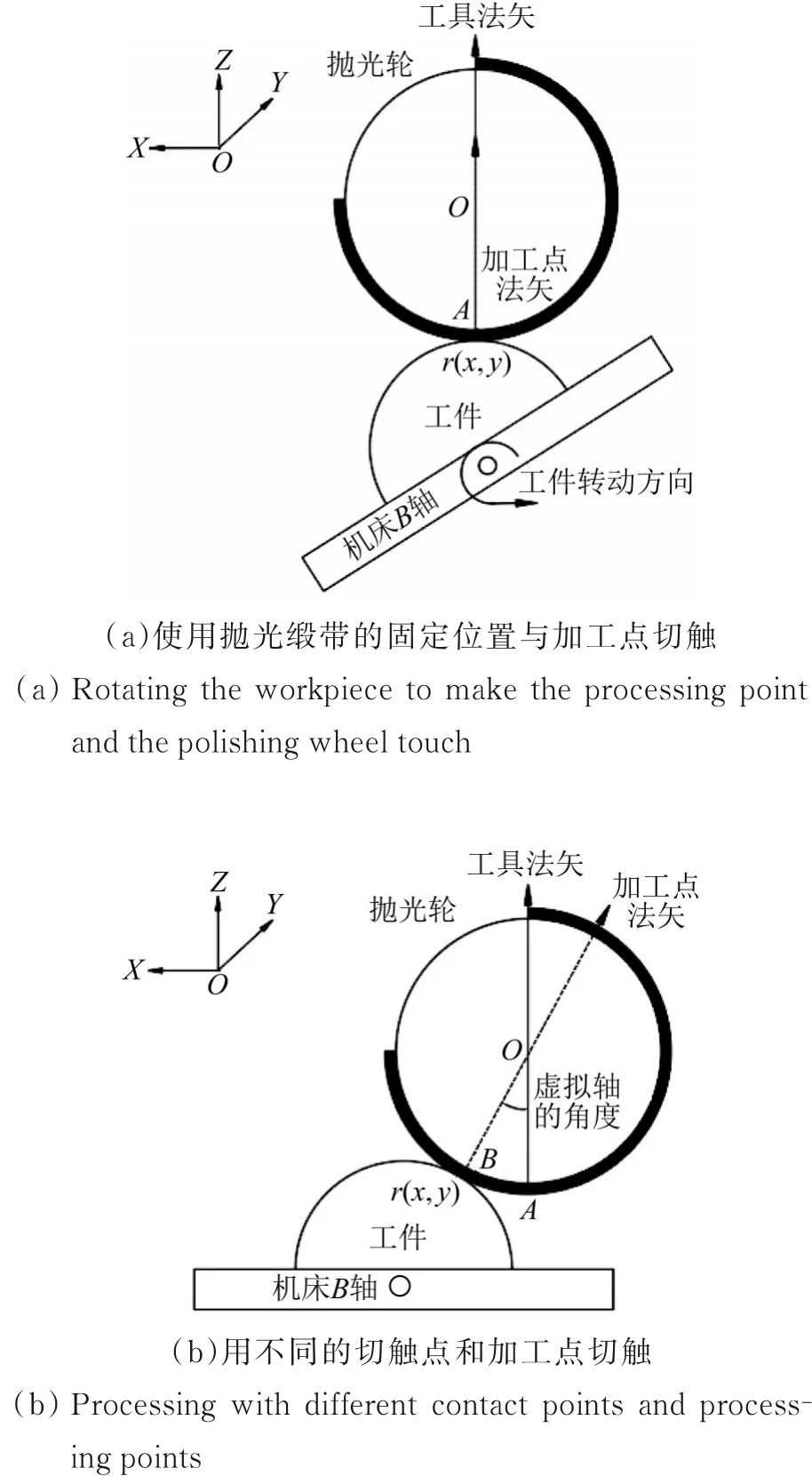
图2 磁流变抛光的一般加工方法和虚拟轴对比Fig.2 Comparison of general machining method and virtual axis of magnetorheological finishing
为保证多轴联动抛光时去除函数稳定,一般通过转动工件使加工点r(x,y)的法向矢量通过抛光轮缎带最低点A对应的工具矢量来实现[8],如图2(a)所示。在一些低陡度光学元件的加工时,若保证抛光轮缎带最低点附近的法向接触点(如图2(b)中的B点)对应的去除函数与最低点处一致,则可以用这些点取代最低点进行法向接触加工,从而取代某些联动轴[9],这些点被称为切触点。切触点的使用使得抛光工具好像在围绕自身中心O旋转,形成了虚拟轴。此时,只需要知道抛光轮半径、缎带厚度以及浸入深度等信息,便可以根据驻留点的法向量计算对应切触点的位置,以进行加工。然而,当前“虚拟轴”主要用于取代机械轴,对于虚拟轴和机械轴的复合使用以进一步增强机床的行程,则尚未开展研究。
3 机械轴与虚拟轴复合抛光工艺
3.1 虚拟轴关键技术
磁流变抛光的高确定性是由去除函数的稳定性作为基础的,因此使用虚拟轴的关键是确定去除函数的稳定范围。由于磁流变液凝聚所需的高梯度磁场由抛光轮内部的电磁铁产生,因此虚拟轴范围内去除函数特性主要取决于磁场特性。
抛光轮剖面如图3所示,抛光轮A点所在一侧为抛光液流入区,C侧为流出区,黑色条纹为缎带区,阴影部为磁铁的磁臂。由于磁臂下方圆弧区X方向的尺寸远大于Y方向的尺寸,可认为除磁铁边缘位置外,YOZ截面下方磁臂气隙的磁场分布相同[11]。设抛光轮上虚拟轴的范围为圆弧线AC,A和C与抛光轮中心连线与竖直线夹角分别记为圆心角θmax和θmin,其中θmin<0<θmax,则虚拟轴转角即抛光轮中心到抛光缎带切触点连线与竖直线夹角,记为θ,其中θ∈[θmin,θmax]。抛光轮表面1.3 mm以内为缎带所在层面,该层面在AC弧线区的磁场分布决定了虚拟轴下去除函数的稳定性。在循环系统稳定和忽略磁场分布的边缘效应的条件下,理论上该处的磁场分布应是一致的才可以保证去除函数的一致性[9]。通过测量磁通密度沿缎带的稳定性以及各测量点与最低点的磁通密度差异大致确定去除函数的采集范围,以5%的体去除率差异作为衡量去除函数的稳定性指标,得到θmax和θmin的值[7-8]。
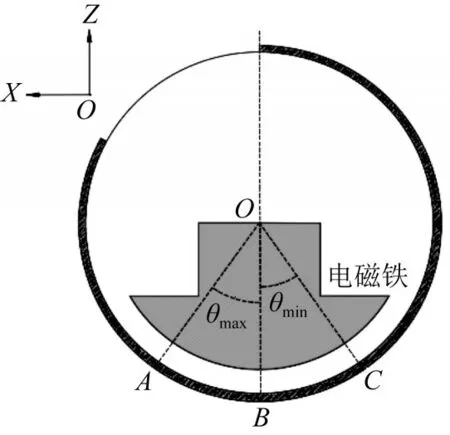
图3 磁流变抛光轮结构Fig.3 Structure of MRF polishing wheel
3.2 机械轴与虚拟轴复合抛光的切触策略
依靠虚拟轴能够满足低陡度曲面的加工需求,但对于高陡度曲面元件而言,虚拟轴的范围远远不够,此时需要调用机械轴联动。然而,机床的机械轴行程能力是有限的,而且在大行程状态下旋转轴会由于转矩过大而产生较大的误差和振动。针对这种元件,可以采用机械轴和虚拟轴复合调用的策略,具体如下:当切触点在工件上的法矢在虚拟轴范围时,采用虚拟轴实现变切触法向加工;当切触点在工件上的法矢超过虚拟轴范围时,切触位置达到虚拟轴边界处,同时调用机械轴实现法向加工。
根据机床运动结构建立工件-抛光轮坐标系(本文采用左手系),如图4所示。首先以加工点r(x,y)处的法矢n(x,y)=(i,j,k)计算使用缎带最低点加工时与虚拟轴复合使用的机械轴转角β=arcsin(i/1-j2)。若β∈[-θmax,-θmin]则不调用机械轴,以虚拟轴进行变触点加工,此时虚拟轴角度θ=-β;若加工点超出虚拟轴范围,如图4(a)所示,则调用机械轴,其转角B以式(2)计算,使得加工点到达虚拟轴的θmin或θmax位置,如图4(b)所示,并以该位置的触点进行加工,此时θ=θmin或θmax。
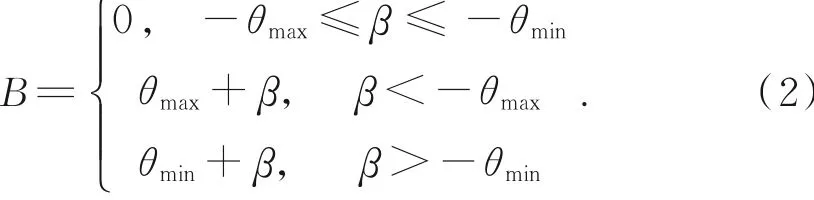
机械轴和虚拟轴结合的方法能减少转动轴的负担,降低多轴联动产生的机构振动和定位误差,同时拓展了加工区域,能提升对高陡度曲面元件的抛光能力。
3.3 机械轴与虚拟轴复合抛光工艺的轨迹坐标解算
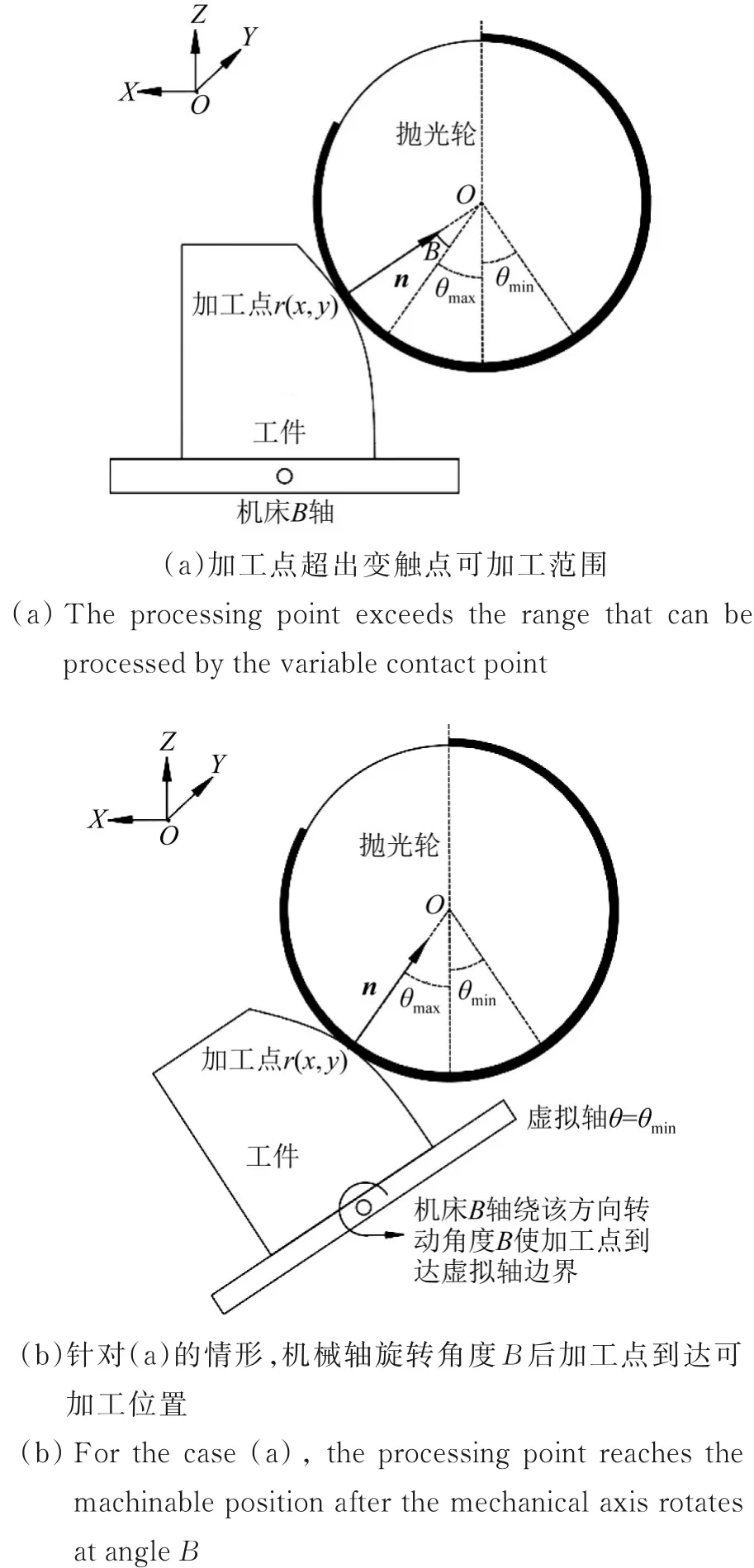
图4 虚拟轴与机械轴的复合调用Fig.4 Polishing with combination of virtual axis and mechanical axis
本文提出的机械轴与虚拟轴复合使用的抛光工艺,其坐标解算需要根据机床结构建立对应的刚体变换模型。实验平台是自研的PKC-1000Q2机床,基本结构如图5所示。该机床具有3平动3转动共6个自由度,其中抛光轮工具是具有1转动2平动的并联机构,其平动方向为主轴的Y方向和Z方向,摆动轴为A轴,垂直于Y轴和Z轴。下方工作台为1平动2转动的并联机构,平动方向为X方向,转动轴C轴安装在B轴上。抛光轮采用悬臂梁结构固定于Z轴上。抛光轮直径为300 mm,表面磁场由内部采用的电磁铁产生。为实现工件定位,在抛光轮一侧装有Renishaw测头。该加工系统具备φ1 000 mm以内口径非球面加工能力,其线性轴的定位误差在10μm以下,转动轴的定位误差在8″以下,A轴行程为±30°,B轴行程为-90°~30°。

图5 PKC-1000Q2数控机床Fig.5 PKC-1000Q2 CNC machine tool
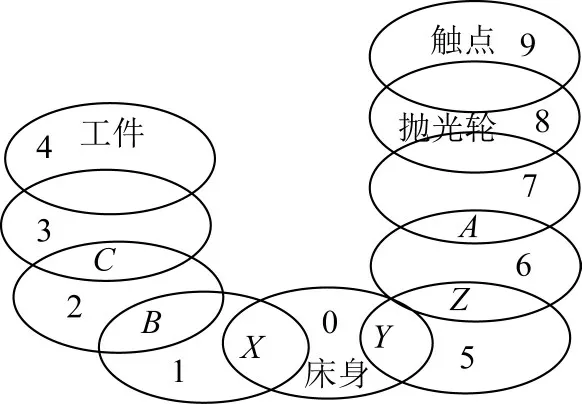
图6 机床结构的拓扑模型Fig.6 Topological model of machine tool structure
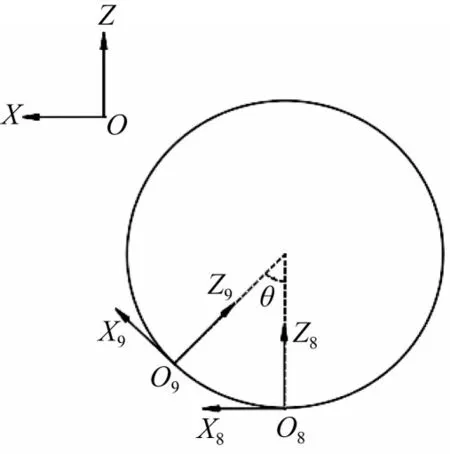
图7 抛光轮切触点与编程点刚体变换关系Fig.7 Rigid body transformation relationship between polishing wheel contact point and programming point
接下来对上述工艺进行轨迹点坐标解算。根据图5中机床各轴运动机构的连接关系,建立磁流变机床机械结构的拓扑模型,如图6所示。其中1~3表示工件一边的运动结构,1表示X轴的运动机构,2表示B轴的运动机构,3表示C轴的运动机构,5~7表示和抛光轮有关的运动结构,5表示Y轴的运动机构,6表示Z轴的运动机构,7表示A轴的运动机构,0表示床身,4表示工件,8表示抛光轮,9表示与工件接触的抛光轮触点。
由拓扑模型可得到各结构之间的齐次坐标变换关系[12]。以缎带最低点作为机床编程点,如图7所示,分别在抛光轮编程点处和实际触点处建立坐标系O8和O9,则从O8到O9坐标系的刚体变换可表示为:
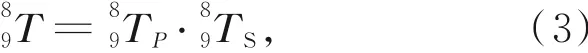
O8坐标系原点平移到O9坐标系的原点后相对于X9,Y9,Z9的旋转变换矩阵。以此类推:表示A轴机械结构运动的坐标系O7到缎带最低点处坐标系O8的刚体变换矩阵;表示Z轴机械结构运动的坐标系O6到A轴转动坐标系O7的刚体变换矩阵;表示Y轴机械结构运动的坐标系O5到Z轴坐标系O6的刚体变换矩阵;床身坐标系到表示Y轴机械结构运动的坐标系O5的刚体变换矩阵;床身坐标系到表示X轴结构运动的坐标系O1的刚体变换矩阵;轴运动坐标系到表示B轴机械结构转动的坐标系O2的刚体变换矩阵;轴转动坐标系到表示C轴机械结构转动的坐标系O3的刚体变换矩阵;轴转动坐标系O3到工件坐标系O4的刚体变换矩阵。
由以上坐标系的刚体变换关系可以得到从工件坐标系O4到触点坐标系O9的变换矩阵T:
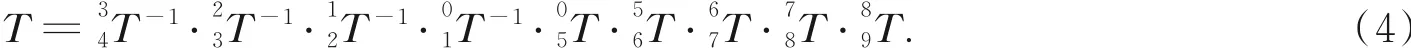
矩阵T的含义为坐标系O9在坐标系O4中的表达。将触点坐标系下的切触点坐标v=[0,0,0,1]T,以及切触点法向矢量w=[0,0,1,0]T右乘矩阵T,得到与工件的切触点在工件坐标系下的位置qw=[x,y,z,1]T与法矢姿态的表示式vw=[i,j,k,0]T,则有:
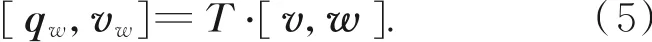
解算式(5)形成的方程组即可得到抛光轮缎带最低点在机床坐标系下的轨迹坐标。
采用光栅线轨迹加工,根据待加工工件的曲面方程,规划缎带切触点的坐标。已知抛光轮切触点在工件坐标系下的位置[qx,qy,qz]和对应的加工点法矢量[i,j,k],由于β=按式(2)计算切触点对应的θ和B轴转角。抛光轮编程点在床身坐标系下的坐标用式(6)计算。其中,[X,Y,Z,A,B]为抛光轮编程点在床身坐标系下的坐标,θ为虚拟轴对应的圆心角,[xw,yw,zw]是工件坐标系原点相对C轴坐标系的位置,Rr为缎带最低点距离抛光轮几何中心的距离,[yt,zt]为缎带最低点相对A轴轴线的位置,x0为B轴和C轴机械结构在X方向的距离。
综上所述,基于机械轴与虚拟轴复合的磁流变抛光方法的工艺流程如图8所示。
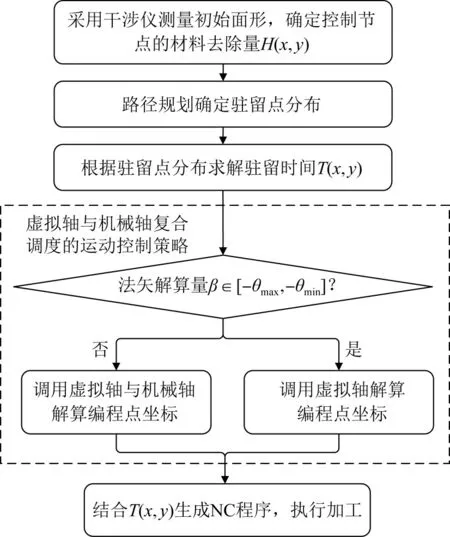
图8机械轴与虚拟轴复合的磁流变抛光工艺流程Fig.8 Process flow chart of magnetorheological finishing with combination of mechanical axis and virtual axis
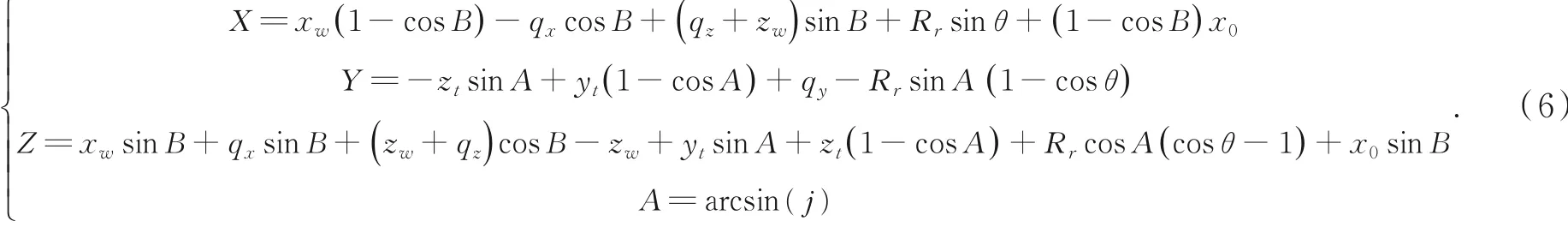
4 实验结果与分析
4.1 磁通密度分布测量
缎带区的磁场分布决定了去除函数特性,是决定虚拟轴范围的关键因素,因此应优先对磁场稳定性进行验证。经计算,磁臂弧线区的长度换算成角度为90°,考虑磁铁边缘效应,对[-30°,30°]的磁通密度进行测量。使用PAX-450型数字特斯拉计,将其测头摆放在抛光轮缎带下方1.3 mm处使磁感应线基本垂直穿过内部霍尔元件。调整测头姿态使特斯拉计达到测量最大值,以同一姿态和距离分别测量各角度对应的磁通密度,得到抛光轮缎带处的磁感应强度和它关于角度的分布。以抛光轮中心为坐标原点建立柱坐标系,得到各触点处的磁通密度随虚拟轴圆心角的分布,如图9所示。观察磁感应强度的分布情况可知,总体磁通密度偏弱,处于缎带收敛的边界值[9],并且从抛光液流入区到流出区的磁通密度略微增加。出现这一现象的原因在于磁铁和抛光轮的配合在X方向出现了偏移,所以两边的磁通密度也不完全一致。从去除函数受磁场的影响程度来判断,去除函数的稳定范围并不能达到磁通密度的测量范围。
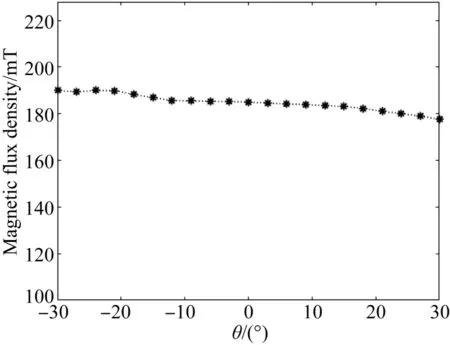
图9 抛光轮表面缎带处的磁感应强度分布Fig.9 Magnetic induction intensity distribution at ribbon on surface of polishing wheel
4.2 不同切触位置的去除函数获取与验证
在验证去除函数稳定性时,还需要对不同切触点下的去除函数进行测试。为满足一般非球面的虚拟轴加工需求[9],同时考虑θ<-16°和θ>20°后磁通密度相对0°时的值变化较大,因此选择采斑件与水平面的夹角为-16°~20°,采斑步距为4°。实验的基本工艺参数如下:抛光轮直径为300 mm,缎带线速度为1.5 m/s,抛光粉类型为氧化铈,磁流变液温度为20℃,室温在21℃,缎带的浸入深度为0.3 mm,浸入时间为3 s。去除函数形态与体去除率结果如图10所示。材料去除量主要与体去除率相关,因此主要关注体去除率的变化[9]。从抛光斑的形态分布以及体去除率信息可以看出,各角度去除函数与0°下的去除函数相比,斑长和斑宽存在很小的差异,体去除率基本在2.0×10-3mm3/s附近分布,磁通密度随角度的增加而略衰减的问题对去除函数在最低点附近较小范围内的影响是不明显的。此外,实验误差造成了去除率分布的波动。经计算去除函数在±12°内的体去除率差异性在5%以内,根据文献[6]和文献[7]的研究,该范围内的去除函数可认为是稳定的,基本满足一般非球面元件的加工需求。此范围外的去除函数因受到磁通密度变化的影响其体去除率和0°下的体去除率差距会更大,不能认为去除函数是等效的,因此θmin和θmax的值分别取-12°和12°。
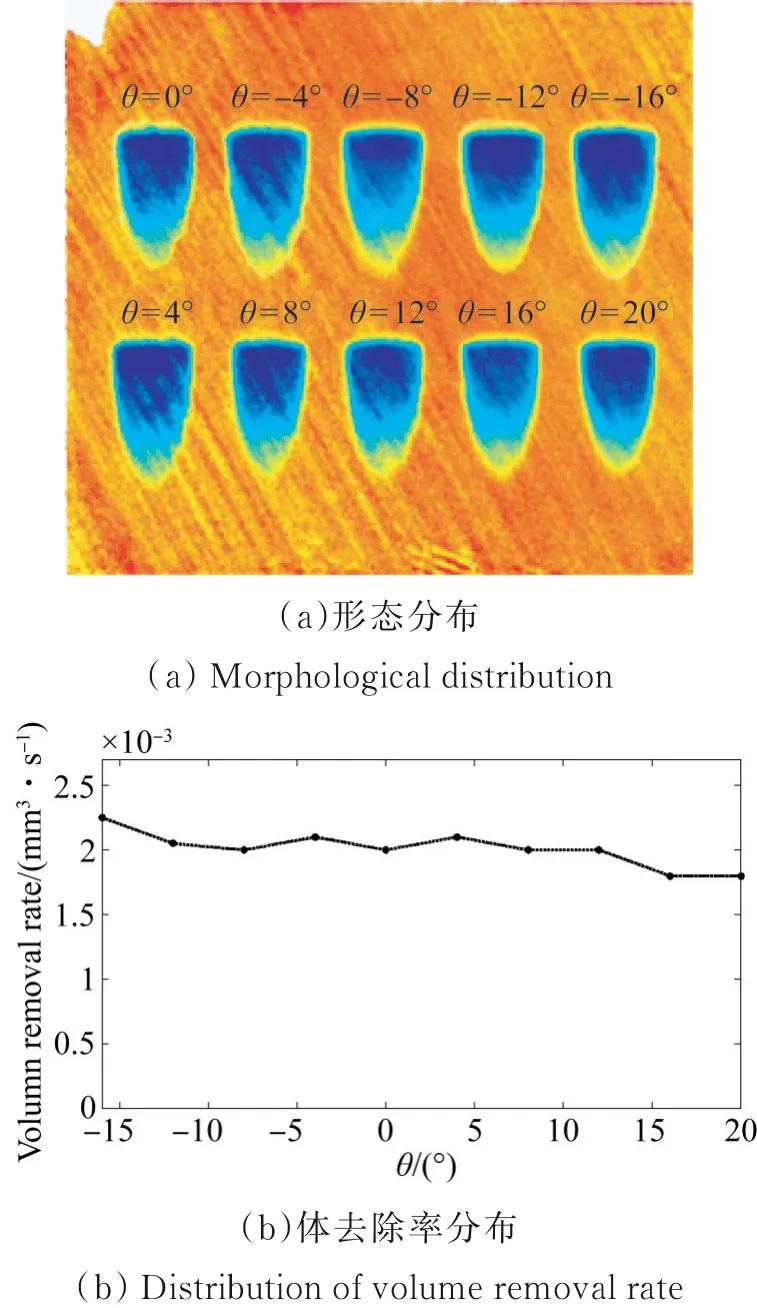
图10 去除函数采集结果Fig.10 Removal function collection results
4.3 带倾角的球面加工实验
对一块口径为84 mm×84 mm、曲率半径为300 mm的熔石英凸球面镜进行加工。在加工时,B轴增加12°倾斜角的基础偏置,使得元件部分区域超出虚拟轴的加工范围,以验证虚拟轴和机械轴的复合使用工艺。
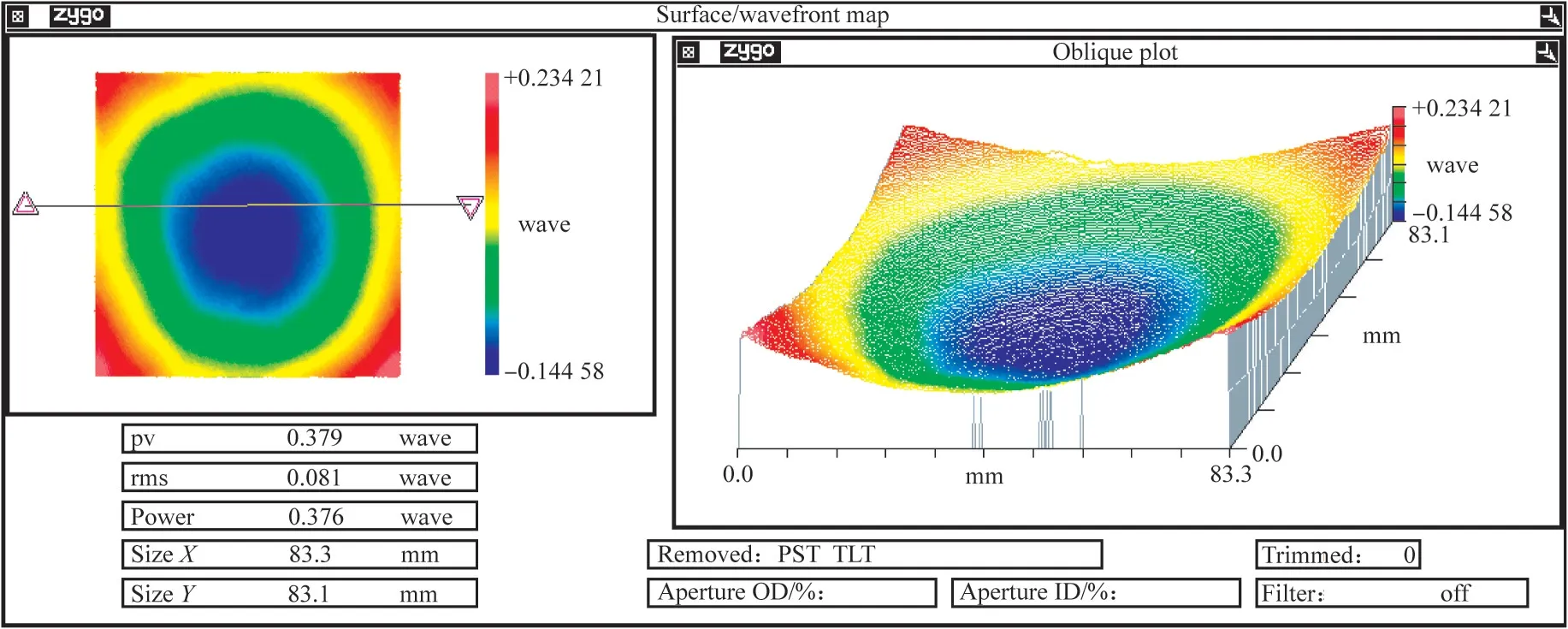
图11 加工前球面件面形Fig.11 Surface figure of spherical parts before processing
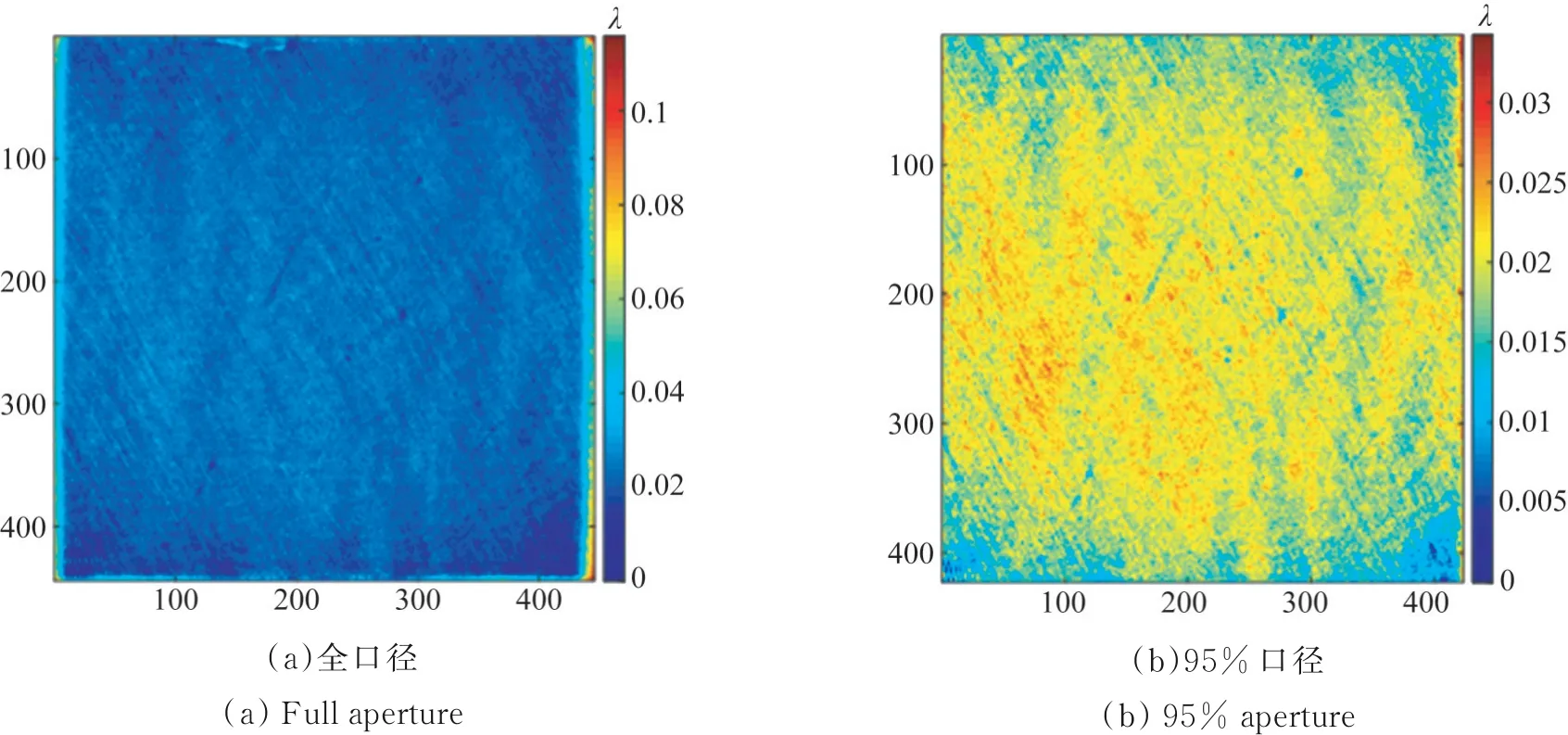
图12 仿真抛光后面形Fig.12 Simulated figure after MRF
去除边缘的倒角区后,该元件的初始全口径面形如图11所示,其PV值为0.379λ,RMS值为0.081λ。采集去除函数后对初始面形进行仿真加工,路径为光栅线形式,经过一轮仿真加工后,效果如图12所示,其全口径PV值收敛到0.12λ,RMS值收敛到0.005 6λ。而去除边缘效应后保留95%的口径,其PV值为0.034 2λ,RMS值为0.002 7λ。利用PKC-1000Q2机床轨迹规划为光栅线路径,加工工艺参数为:抛光轮直径300 mm,转速120 r/min,抛光粉为氧化铈颗粒,含水量14%,流量1 800 mL/min,室温22℃,浸入深度0.3 mm。经过一轮10 min的磁流变抛光后,其PV值收敛到0.219λ,RMS收敛到0.017λ。这里不考虑边缘效应的影响,仅分析95%口径的局部区域面形,如图13所示,其PV值收敛到0.096λ,收敛效率为73.98%;RMS值收敛到0.012λ,收敛效率为84.81%。由此验证了本文提出的虚拟轴与机械轴复合的磁流变抛光工艺的有效性。
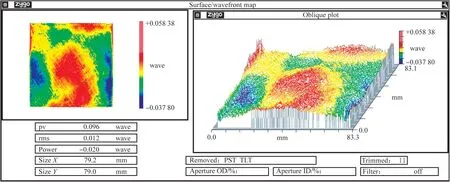
图13 一轮抛光后95%口径的面形Fig.13 Surface figure of spherical part for 95% aperture after one round MRF
4 结 论
为了提高磁流变抛光工艺对高陡度曲面元件的加工能力,本文针对常规的抛光轮磁场结构,分析了保证去除函数稳定的磁场特点,通过变触点磁场特性和去除函数形态变化确定了虚拟轴的范围,提出了虚拟轴和机械轴的复合使用工艺。该工艺以机械轴作为虚拟轴的辅助轴,将元件超过虚拟轴边界的高陡度部分变换至虚拟轴范围内,进一步拓展了加工区域,提升了高陡度曲面元件的加工能力,同时降低了完全依赖机械轴所带来的振动和定位误差。实验加工了一块偏置倾角为12°、曲率半径为300 mm的球面工件,将其95%口径的面形PV值收敛至0.096λ,RMS值收敛至0.012λ。实验结果表明,虚拟轴和机械轴复合的抛光方法具有针对高陡度曲面的修形能力。

