改进Zigzag遍历与哈希的Lorenz混沌构建

郭 媛，王 充

（齐齐哈尔大学计算机与控制工程学院，黑龙江齐齐哈尔161006）

1 引 言

传统的采样定理奈奎斯特指出，只有当采样速率达到信号带宽的2倍以上，才能够实现信号的重建，而这里有很多冗余的数据都需要抛弃，这就势必会引起大量的采样数据被浪费，从而增加了成本。为了节约成本，克服上述问题，压缩感知理论（Compress Sensing，CS）由Candes和Donoho等人在2006年被等人提出。近些年来，压缩感知理论在图像加密领域得到了广泛地应用。压缩感知理论主要包括三部分：信号的稀疏性，测量矩阵的构建以及信号的重构［1-3］。而测量矩阵作为压缩感知中较为关键的一步，决定着整个压缩感知过程的好坏，传统的测量矩阵由于占用空间较大，传输成本较高，不利已保存和运输。因此，在2006年，Candes和Tao［4］首次把高斯随机测量矩阵应用在压缩感知中。2014年Zhou等［5］采用密钥控制生成测量矩阵，但在Zhou提出的方法中，参数比较少，缺乏一定的密钥空间。2015年梁亚茹等［6］把由可变的参数来控制生成测量矩阵，验证了可变参数的测量矩阵的可行性。2017年王厚林、李智［7］通过控制参数映射生成观测矩阵和加密控制矩阵。2019年朱礼亚等［8］通过并行的压缩感知与混沌映射的加密设计，验证了测量矩阵的可行性，但是其混沌系统的密钥不具有一定的随机性。

混沌系统是一种和密码学特性相似的系统，混沌系统具有对初始值的极度敏感性，内在的随机性，以及随着混沌的迭代长时间不可预测等特性，与密码学的特征相吻合，因此常用在加密领域［9-11］。基于混沌系统的测量矩阵，由于只需要保存混沌系统的初始密钥少量参数，可以大大减少空间资源和传输成本的浪费。因此，得到了越来越多学者的关注，但是传统的基于混沌系统的测量矩阵，没有产生与明密文的关联性，缺少抗明密文攻击的能力。

一维混沌系统在构建测量矩阵中得到广泛应用，但是一维混沌系统动力学方程较为简单［12］。因此，本文则利用Lorenz混沌产生测量矩阵，由低维空间向高维空间进行转变，增大了系统的复杂性。混沌系统的参数采用哈希函数SHA-512来进行产生，通过密钥与明文相关联，这样就会产生一定的雪崩效应，即使只对密钥进行极微的改变，测量矩阵构造的结果也会千变万化，使测量矩阵具有多样性。

2 压缩感知理论

压缩感知中信号的稀疏性是十分关键的一步，对于信号稀疏性［13］定义如下：

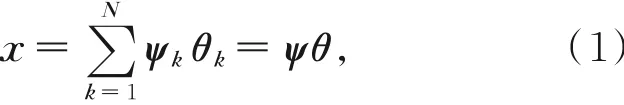
其中：x∈RN为一维离散信号，N为长度，ψ={ψ1，ψ2…，ψθ}为一组正交基，θ∈RN×1为信号x在正交基上k的展开系数，若x中仅存在个非零系数，则称信号x是可稀疏化的，并且信号x是k稀疏的。测量矩阵可以说就是把不同空间上的信号进行转化，对于可稀疏信号x将其投影到另一组测量基φ=[φ1，φ2…φM]T上，得到x的M个线性测量值，即：

其中：y为压缩后的测量值，Θ=φψ是M×N的感知矩阵，其中满足条件M＜＜N，因此，可以看出压缩感知能够对信号进行压缩和采样的，CS理论表明，感知矩阵Θ在满足k阶约束等距条件（k_IP）时，即：

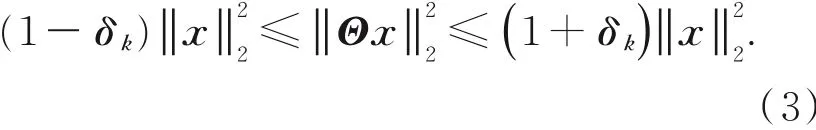
从测量值y中重构出信号的稀疏系数θ可以转化为L0的范数优化问题：

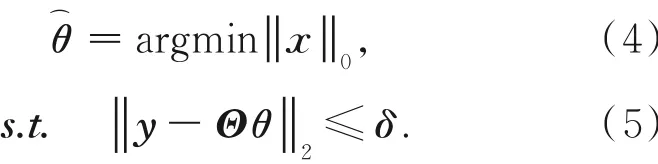
L0的范数是NP难问题，通常把它转化为L1范数，从而进行求解。

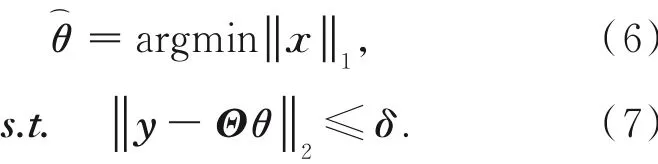
3 混沌系统与Zigzag置乱图像加密

3.1 混沌系统

由于Logistic混沌表达式比较简单，但是它也具有混沌系统的良好特性，因此在混沌系统中经常被使用，其方程表示为：

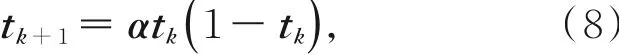
其中：tk∈(0，1)；k=0，1，2...k；α是Logstic系统的一个系统参数，α的取值范围是(0，4]，当α在区间范围内取不同的值时，式（8）就会出现不同的状态，当α∈[3.569，4]时，Logistic系统呈现混沌状态。

Lorenz混沌是由气象学家洛伦兹在研究气象时所发现的一种混沌现象，其是一个三维的连续混沌映射，其公式所描述的是微分的形式，具体公式如下：

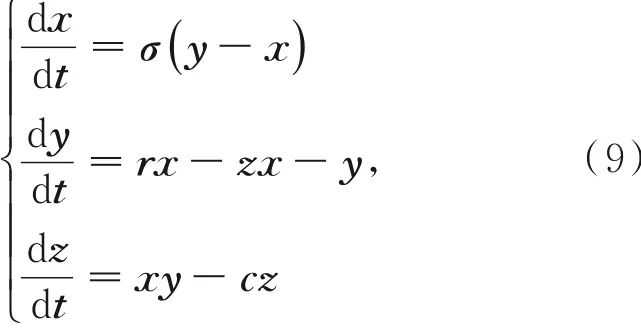
其中：x，y，z组成了三维空间，σ，r，c是Lorenz混沌系统的控制参数，一般情况下，在σ=10，r=28，c=83时，式（9）呈现出混沌的状态［14］。

3.2 Zigzag置乱

Zigzag是一种类似于中文汉字“之”形的一种遍历方法，传统的Zigzag置乱由于其总是从矩阵的左上角作为第一个元素，按照“之”形的方式开始进行遍历，这样势必会存在一些弊端，比如，开始的元素和最后的元素遍历的位置总是固定的，缺乏一定的随机性，因此，在置乱的过程中，很容易被破解，而本文是通过利用图像的像素值总和以及像素的平均值来构造遍历的起始位置，这样就增加了更多的可能性，遍历后的矩阵会更复杂，便于后面构造加密矩阵，提供了安全性。对于Zigzag的起始位置的确定可以由公式（10）～（15）进行表达：

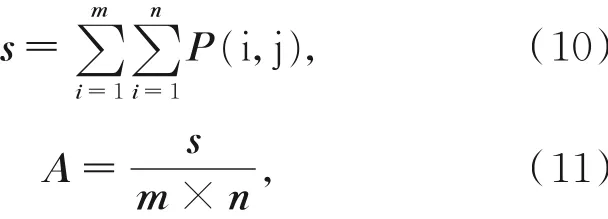
其中：s表示图像中灰度值的一个总和，A表示像素点的平均值，m和n代表着图像矩阵的行数和列数。

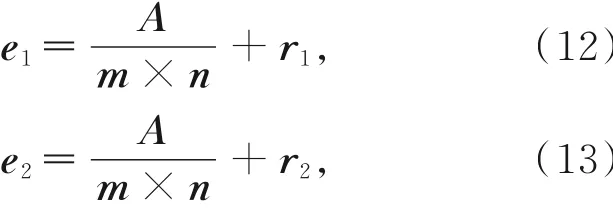
其中r1和r2表示的是外部的参数。

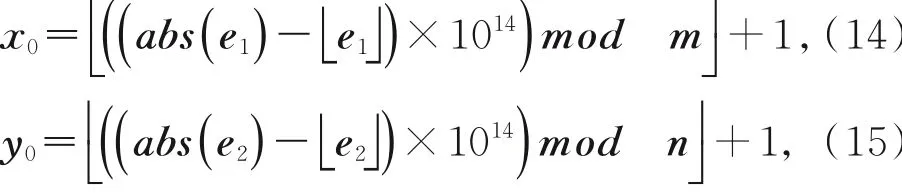
其中：abs代表着绝对值表示向下取整符号，例如表示取余。

3.3 基于Lorenz混沌的测量矩阵的构建

对于Lorenz混沌，假定系统初始值为x0=1.156，y0=1.342，z0=1.247；Logistic混沌系统中，t0=0.234，α=3.966；利用哈希函数SHA-512对原图像进行加密产生512位哈希值［15］，每8位为一组进行划分，可以化成k1，k2，...，k64的十进制数，密钥与明文产生关联，具有刚好的安全性。与明文具有关联关系后的Lorenz混沌系统初始值可以表示为：

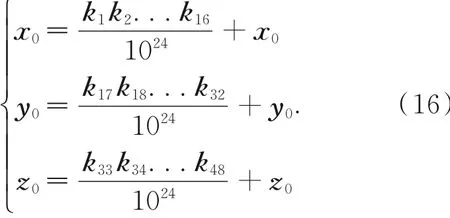
Logistic混沌系统初始值表示为

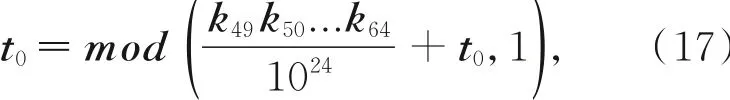
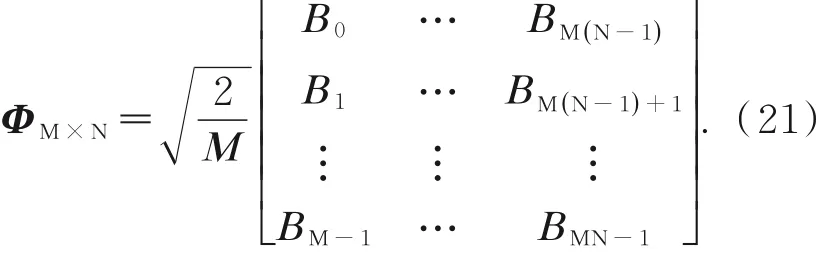
把式（16）以及上述给出的Lorenz混沌参数带入到式（9），迭代1 000+3×mnd次，然后舍弃前1 000项，产生3个混沌序列X=｛1，2，...，mnd｝，Y={1，2，...，mnd}，Z={1，2，...，mnd}，其中，m=CR×M，d为采样的间隔距离，CR=1 4为压缩率，M，N则代表着所要进行加密图像的行数和列数。则测量矩阵构造如式（18）～式（21）所示：

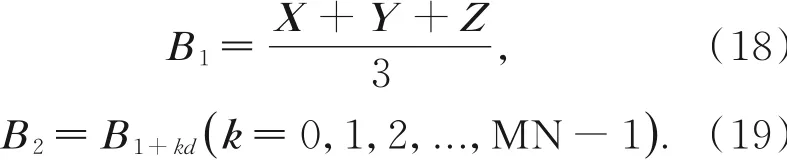
为了使构造的测量矩阵更加满足CS的条件，可以对B2在进行以下操作：

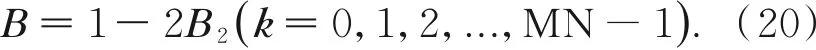
接下来就可以把B按照列优先的方式进行排列，则可以得到测量矩阵ΦM×N。

3.4 加密算法

（1）首先，选用一幅大小为M×N的Lena图像。其次，通过DCT对Lena图像进行稀疏化操作，可以得到一个稀疏的矩阵C1，然后再根据上面介绍的Zigzag对DCT变换后的图像C1进行置乱，得到大小为M×N的置乱矩阵C2。

（2）将式（21）由Lorenz混沌产生的测量矩阵，与C2进行操作，得到压缩后的矩阵C3。

（3）对矩阵C3进行量化操作，像素值的量化范围在0～255之间，Sigmoid函数是常用来把数据量化到0～1之间，因此可以利用系数与Sigmoid函数相结合进行量化，量化后的矩阵C4可以表示为：

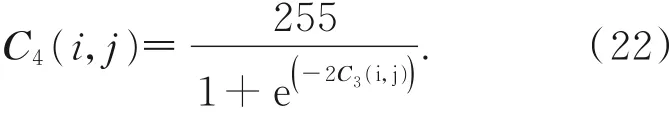
（4）将式（17）和μ值代入式（8），迭代1 000+2×M×N次，舍弃前1 000项，得到长度为2×M×N的序列，混沌产生的序列可以拆分成两部分，第一部分为L1={0，1，2，...，MN-1}，第二部分为L2={MN，MN+1，...，2MN-1}。

（5）将L1={0，1，2，...，MN-1}转 化 为M×N的矩阵R1，并将矩阵R1每个像素都量化到0～8之间，量化后的矩阵为R2。

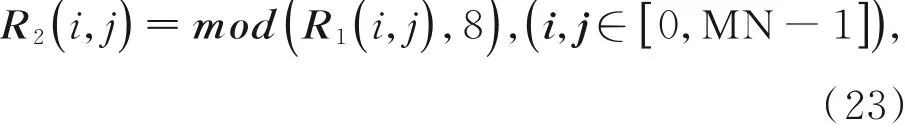
其中：R1(i，j)，R2(i，j)表示矩阵R1，R2第i行第j列对应的值。

（6）将矩阵C4的像素值都转化为其所对应的8位二进制编码形式，得到一个二进制矩阵C5，将C5与R2进行相应位置的关联实行循环移位操作，循环移位后得到的矩阵为C6，即：

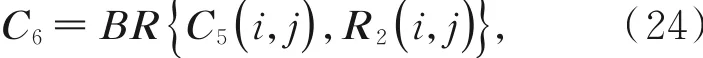
其中：BR表示循环右移操作，C5(i，j)，R2(i，j)表示矩阵中第i行第j列位置的灰度值，由于R2(i，j)每个值都是小于8的，所以，当R2(i，j)对应的值为几，C5(i，j)就相应的向右整体移动几位。然后把C6再转为十进制的矩阵C7。

（7）将L2={MN，MN+1，...，2MN-1}转化为M×N的矩阵R3，将R3转化为对应的8位二进制矩阵R4，将R4，C7进行二进制异或，得到C8，即：

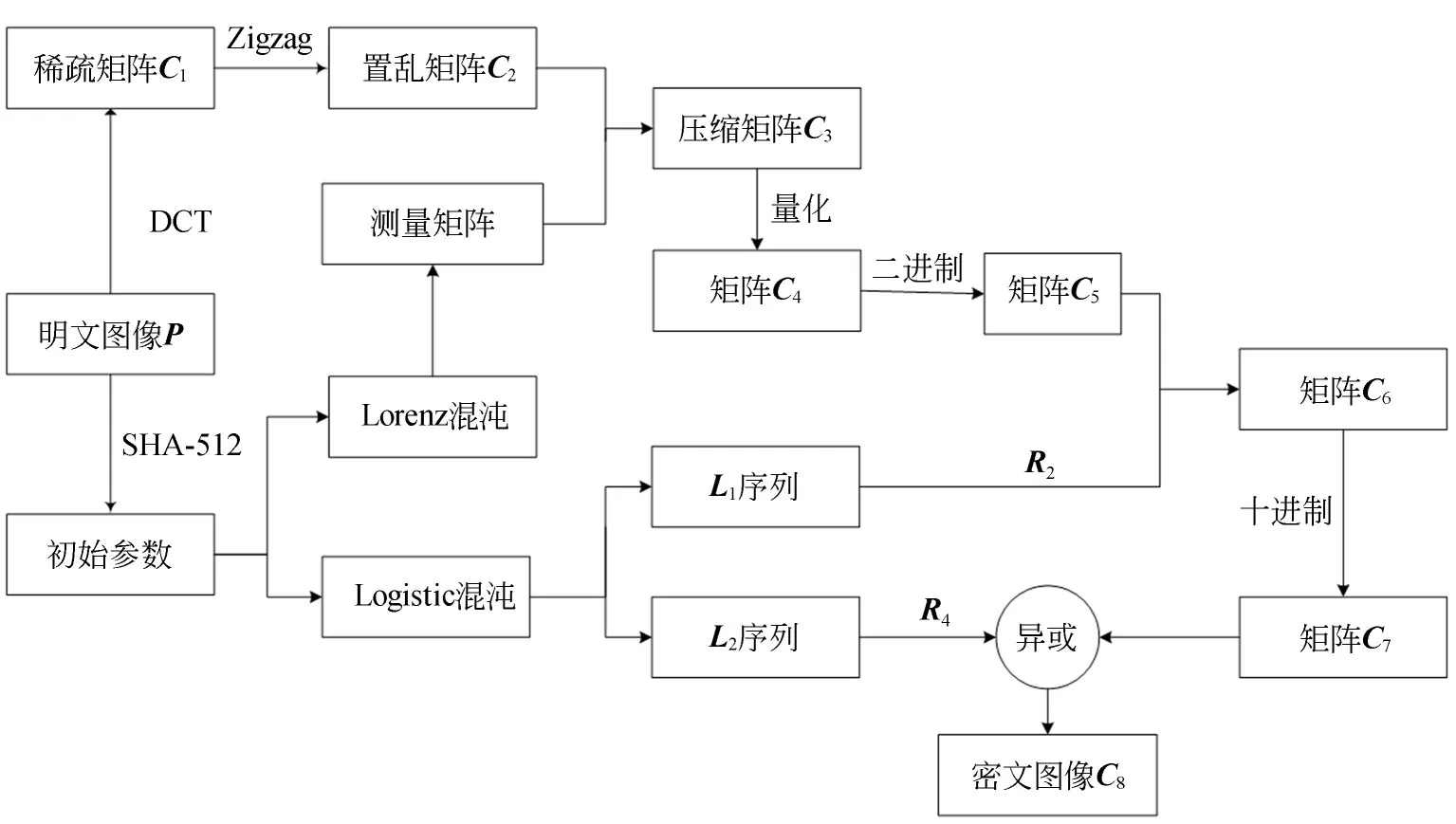
图1 加密算法框架图Fig.1 Block diagram of encryption algorithm

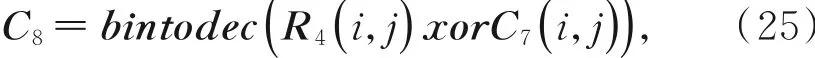
其中：bintodec表示把二进制与十进制数之间的一个转化，矩阵C8即为最终加密后的图像。

由于该算法是对称加密算法，所以解密算法就是解密的反操作。

4 实验与分析

实验仿真选用的软件是Python 3.7.2对于大小为256×256的Lena图像，加密过程中的初始密钥包括Lorenz混沌和Logistic混沌的系统参数。其中：Lorenz中σ=10，r=28，c=83，x0=1.156，y0=1.342，z0=1.247；对于Logistic混沌系统，t0=0.234，α=3.966。外部参数r1=0.332 8，r2=0.445 6。

Lena图像经过加密的图像和利用解密算法而解密得到的图像如图2所示，可以看到，加密后的图像已经很难找到原始图像的信息，具有一定的安全性。与此同时，经过解密算法又能恢复到原始图像，表明具有一定的重构能力。

4.1 直方图分析

图2 Lena加密解密图像Fig.2 Lena encrypted and decrypted image

灰度直方图是图像的统计特性的一个直观表达，从直方图中能够看出图像像素之间的关系，未经处理的图像一般都是拥有很明显的特征，大部分的灰度值密切关联，可能只是分布在几个灰度值附近，而经过加密处理的图像，这些灰度值之间的相关关系被破坏，像素值就会分布的更加的均匀，而不容易让攻击者通过直观的分析就能找到更有价值的信息，因此可以根据原始图像与加密图像直方图之间的差异来衡量加密算法的好坏［16-18］。如图3所示，为Lena图像与加密后的图像的一个直方图分析。其中，横坐标是图像的灰度级，纵坐标是各个灰度值在图像中所出现的次数。

4.2 密钥空间分析

为抵御穷举攻击，加密算法的密钥空间要尽可能的大，密钥空间是相对于密钥而言，表示密钥所能达到的的取值范围，一般认为，当密钥空间的大小至少达到2100，就认为加密算法是安全的，当然随着密钥空间的逐渐增大，加密算法相应的也就越安全。但是，加密算法也会越复杂。

本文算法的密钥初始值主要包括两部分，Lorenz混沌中的x0，y0，z0，Logistic混沌中的t0，α，这些数据都是double类型，最大精度为10-15，所以密钥空间可以粗略地看作0.5×1015×5=5×1074＞＞2100，该算法密钥空间已经远远的大于所要求的数值，已经满足了密钥空间的安全性。另外还有外部参数r1和r2，也是属于密钥的一部分，也大大增加了密钥空间。

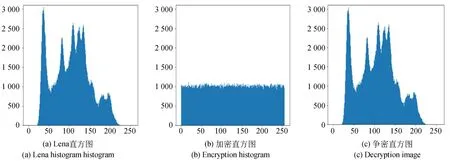
图3 Lena图像与加解密直方图Fig.3 Histogram of Lena image and encryption and decryption

4.3 密钥敏感性分析

对于图像加密，密钥敏感性通常指的是初始的密钥发生一定的变化，能否正确的恢复出原来的图像，一个良好的加密算法要求在加密中体现出密钥的敏感性。如图4所示，正确的密钥能够把Lena图像完整恢复，在Lorenz混沌中我对初始值进行改变，改变量为Δx0=10-15，Δy0=10-15，Δz0=10-15，进行图像的解密，无法得到原始的Lena图像，可见，密钥尽管发生10-15的一个微小变化，也很难得到正确的解密图像，从而验证了该算法满足密钥敏感性的要求。

图4 Lena图像敏感性分析Fig.4 Sensitivity analysis of Lena images

4.4 信息熵分析

信息熵是衡量图像灰度值的分布信息，图像内部信息越混乱，表明图像的信息熵就越大，不确定性越强，加密效果越好。一般的对于256灰度级的图像加密的信息熵，其值越接近8，则表明加密效果越好。信息熵的定义如下所示：

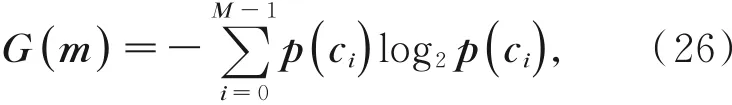
其中：ci表示的是信息源，p(ci)为信息m出现的概率。计算加密后的Lena图像的信息熵，并和其他文献进行对比，本文加密算法的信息熵更加接近于8，表明比所列对比文献加密效果更好。

4.5 相邻像素相关性分析

相邻像素点之间具有密的切关联，所以很容易受到攻击者采用统计分析。而图像的加密，则是把相邻像素之间的这种强关联信息给打破，从而保证了图像信息的安全。因此，相邻像素的相关性对于评价一个加密算法好坏也是至关重要的［19-21］。而相关性，则经常用相关系数来进行表示，相关系数r的范围是[-1，1]，越接近1则表示正向相关性越强，越接近-1则表示负向相关性越强，相关性越强加密效果就越差，一般的相关系数r越接近于0，则代表图像像素的强关联性被打破，具有很好的加密效果。相关系数的公式可以表示为：

表1 密文图像的信息熵Tab.1 Information entropy of ciphertext image

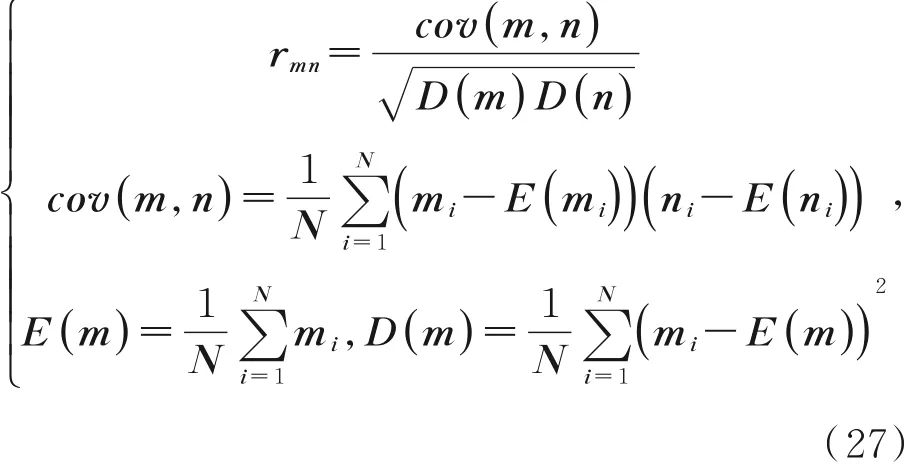
其中：mi和ni表示相邻的两个像素值，N表示选取的像素点对数，rmn表示相关系数，covmn为协方差，E(m)为期望，D(m)为方差。选择Lena图像和加密图像2 000对像素点，按照公式（27）分别进行计算，得到水平、垂直、对角线方向上的相关系数［22-23］。如表2所示，为Lena图像在不同方向上的相关系数的分析。从表中数据可以看到，经过本算法加密后的数据在水平和垂直方向上相关系数更加接近于0，相邻像素的相关关系已经得到破坏，具有良好的加密效果。

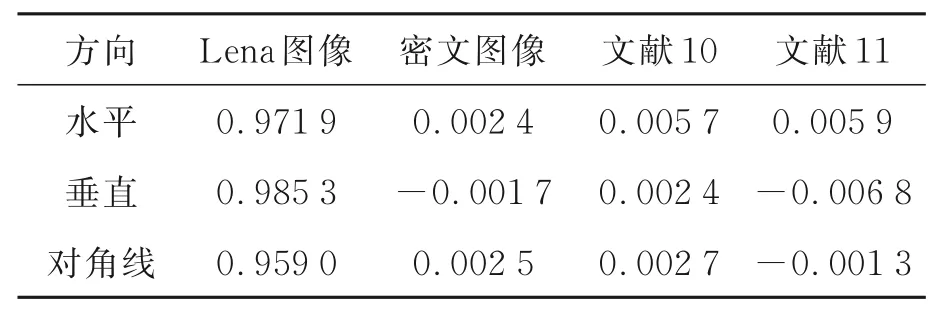
表2 相邻像素的相关性分析Table 2 Correlation analysis of adjacent pixels

5 结 论

本文对传统Zigzag置乱进行了改进，可以利用明文像素确定Zigzag的初始置乱位置，每次初始位置的改变都可以得到不一样的置乱矩阵，极大地增加了系统的随机性。利用哈希函数SHA-512，明文的哈希值可以作为密钥的一部分，增大了密钥空间，将密钥与明文相关联，使混沌序列具有自适应性，具有一定的雪崩效应和抵抗名密文攻击的能力。还利用明文图像通过DCT稀疏化，再通过改进的zigzag置乱与Lorenz混沌构造的测量矩阵进行压缩感知，经过量化，置乱扩散等操作得到的加密算法。实验通过对明密文信息熵和其他文献的对比，本文加密后的信息熵为7.998 6，更加接近于8，密文图像相关系数接近于0，密钥空间为5×1074，表明本算法具有足够大的密钥空间，加密效果更好，具有很强的安全性和实用性。