基于跨尺度字典学习的图像盲解卷积算法

彭天奇，禹 晶，郭乐宁，肖创柏

（北京工业大学信息学部，北京100124）

1 引 言

运动模糊是一种常见的图像降质现象，通常由于相机的抖动或者物体的运动造成。单幅图像去模糊问题研究如何从一幅模糊图像中恢复出原始的清晰图像。根据模糊核是否已知，去模糊方法可分为两类：若模糊核已知，则称为非盲复原方法；若模糊核未知，则称为盲复原方法。

对于均匀模糊图像的形成过程可以表示为如下卷积模型：

其中：y为模糊图像，h为模糊核，*表示卷积操作，x为清晰图像，n为噪声。在卷积模型下，图像盲复原即研究如何从模糊图像y中同时估计出模糊核h和清晰图像x。由于将模糊过程建模为卷积的形式，因此盲复原问题也称为盲解卷积问题。

图像盲解卷积是一个严重的欠定逆问题，基于最大后验概率（Maximum a Posteriori estimation，MAP）估计或变分模型的方法［1-15］通过构建模糊核和图像的先验模型来约束问题的解空间。基于MAP估计的方法在条件概率服从某一种噪声模型，并结合清晰图像和模糊核的先验概率模型的假设条件下，通过最大化后验概率来估计清晰图像和模糊核，而变分模型则是在噪声概率模型服从高斯分布的条件下，通过负对数函数将最大化后验概率问题转换为最小化变分问题。前期，Chan等［4］利用全变分的方法来约束清晰图像的梯度。Levin等［5］提出了一种超拉普拉斯先验建模图像的梯度来估计模糊核。Krishnan等［6］提出了一种归一化的稀疏先验，利用L1/L2范数约束图像梯度，将L2范数对图像梯度的约束作为L1范数的权重。Anger等［7］利用L0范数对图像梯度进行约束，增强图像中的显著边缘，减小细节对模糊核估计的影响。

图像梯度表示邻域内像素之间的关系，由于自然图像包含复杂的结构，仅利用相邻像素之间的关系很难清楚地描述这种复杂的结构，基于图像块的先验可以表示更大更复杂的图像结构。Michaeli等［8］利用不同尺度图像之间图像块的相似性作为先验来估计模糊核。Pan等［9］在模糊核的估计中引入了暗通道先验，但是这种方法不适用于缺乏暗像素以及存在噪声的图像，因为在这些情况下，无法保证暗通道的稀疏性。在Pan等［9］方法的基础上，Yan等［10］结合亮通道先验与暗通道先验作为约束项以提高算法的鲁棒性。Chen等［11］利用L1范数约束局部最大梯度值作为正则项来估计模糊核。

稀疏表示是指利用少量元素的线性组合来表示信号，稀疏表示作为图像先验广泛应用于图像复原领域。Hu等［12］和Zhang等［13］将图像块的稀疏表示作为先验进行模糊估计，并从其他自然图像或模糊图像本身中随机采样图像块作为训练样本，利用K-SVD算法［14］训练字典。Chang等［15］结合图像块的稀疏表示和结构自相似性作为先验进行模糊核估计。

本文提出了一种基于跨尺度字典学习的图像盲解卷积算法，利用图像的跨尺度自相似性，从降采样模糊图像中学习字典，将图像纹理区域在该自适应字典下的稀疏表示作为图像先验。一方面，降采样减弱了图像的模糊程度，与模糊图像相比，其降采样图像与清晰图像具有更强的相似性，采用降采样模糊图像中的图像块训练字典能够更好地对清晰图像进行稀疏表示，另一方面，由于仅在纹理区域清晰图像的稀疏表示误差小于模糊图像的稀疏表示误差，将稀疏表示作为正则化项仅对图像中的纹理块进行约束，迫使重建图像的边缘接近清晰图像的边缘。因此，本文的算法能够准确地估计出模糊核，并具有良好的鲁棒性。

2 基于跨尺度字典学习的稀疏表示先验模型

本文提出了一种基于跨尺度字典学习的稀疏表示先验模型，利用图像的跨尺度自相似性，从模糊图像的降采样图像中抽取图像块作为稀疏表示字典的训练样本，并对图像中的纹理块进行稀疏表示。

2.1 稀疏表示先验模型

在图像中以n×n为图像块尺寸，按照固定步长（每相隔固定个像素）进行有重叠的图像块划分，并对图像块进行列向量表示。设图像中抽取的图像块表示为Qj x1，其中Qj∈Rn×N为抽取矩阵，用于从图像中抽取第j个图像块，n为抽取的图像块尺寸，N为图像的像素数（后文涉及到范数的表示和导数计算，为了方便表达，需要将公式写为矩阵向量的形式，因此，对于空域卷积，本文近似使用列向量的形式表示）。对于图像中的任意图像块Qj x，可以将其表示为字典中少量原子的线性组合，即：

其中：矩阵D∈Rn×t为字典，字典中列向量为原子，若原子的数量大于列向量的维数，即t＞n，则D为过完备字典；αj∈Rt为稀疏表示系数，αj中非零元素的数量越少，Qj x的表示越稀疏表示ℓ0范数，用于统计向量中非零元素的个数。

在字典确定的情况下，对于任意图像块Qj x，求解稀疏表示系数αj可表示为如下所示的ℓ0范数约束最小化问题：

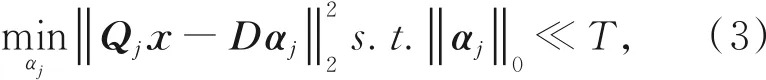
稀疏表示的关键任务是设计字典，使得图像块可以用字典中的原子稀疏表示。当前存在两种字典设计方法，一种是根据图像的基本形态结构，选择合适的基函数构建解析字典，解析字典的生成简单直观，但只能对特定类型的信号进行稀疏表示；另一种是通过对图像内容的学习，自适应地生成可表示信号实际结构特征的训练字典，由于训练字典根据图像内容生成，因而更适合一般性图像的稀疏表示。

利用训练样本进行字典学习，可表示为如下约束最优化问题：

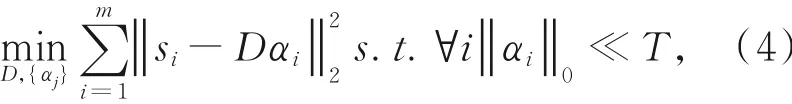
其中：si∈Rn，i=1，...，m为训练样本，m为样本个数。本文利用K-SVD（Singular Value Decomposition）算法生成过完备字典D。式（4）在保证稀疏表示-系数稀疏性的条件下约束表示误差，这是因为K-SVD算法的求解是稀疏表示和字典更新交替迭代过程，需要根据当前更新的字典，利用OMP算法获得式（3）的近似解。

2.2 跨尺度字典学习

字典学习的关键是选择训练字典的样本图像。为了更好地表示清晰图像，理想情况是将清晰图像作为字典的训练样本，然而，在实际情况下，清晰图像是未知的、不可用的。常用的方法是从大量清晰图像组成的数据集中提取训练图像块或者直接将模糊观测图像作为训练样本来学习字典。文献［12］利用数据集作为字典学习的样本，一般数据集的规模较大，字典学习的效率较低、且当数据集中的图像与待复原图像的特征差异较大时，无法保证待复原图像在该字典下的稀疏性。文献［13］利用模糊图像本身训练字典，该字典无法准确提供关于清晰图像的特征，因而，无法保证清晰图像在该字典下具有稀疏性。

多尺度自相似性是指在同一场景中存在着相同尺度以及不同尺度的相似结构。这种多尺度自相似性具体表现为图像中具有相同尺度以及不同尺度的相似图像块，从图像中提取一个图像块，可在原尺度图像及其他尺度的图像中找到相似的图像块。相机的透视投影是图像的多尺度自相似性普遍存在的主要原因。Glasner等［16］通过大量图像的实验验证了相似图像块普遍存在于同一场景的相同尺度以及不同尺度图像中。本文中将不同尺度的图像自相似性简称为跨尺度自相似性，利用跨尺度自相似性为图像复原提供附加信息。

由于降采样降低了图像的模糊程度，与模糊图像本身相比，其降采样图像与清晰图像具有更强的相似性。Michaeli等［8］从理论上证明了模糊图像的降采样图像与清晰图像更相似。由于从降采样模糊图像中提取的图像块与清晰图像块更相似，将降采样模糊图像作为字典的训练样本能够更好地对清晰图像进行稀疏表示。图1比较了不同训练样本字典学习下的清晰图像稀疏表示误差，对于图1（a）所示的清晰图像，以清晰图像本身作为字典的训练样本对清晰图像进行稀疏表示，图1（b）为稀疏表示重建图像与清晰图像的差值图像。采用模糊图像与其降采样图像作为字典学习的训练样本，所得稀疏表示重建图像与清晰图像的差值图像分别如图1（c）和（d）所示。通过比较图1（b），（c）和（d）可以看出，使用清晰图像中的图像块训练字典，稀疏表示误差最小，而与模糊图像本身相比，采用其降采样图像中的图像块训练字典能够有效降低稀疏表示误差，使其更接近清晰图像作为训练样本的稀疏表示误差。图1直观说明了图像降采样对清晰图像稀疏表示字典学习的贡献。

图1 不同训练样本的稀疏表示误差比较Fig.1 Comparison of sparse representation errors from different training samples

另一方面，由图1（b）可以看出，图像中纹理或细节区域不容易稀疏表示，稀疏表示误差较大，而灰度平坦区域的稀疏表示误差较小。本文将灰度值变化较小的图像块称为平坦块，灰度值变化较大的图像块称为纹理块。在图像模糊的过程中，随着图像模糊程度的增大，图像中纹理块逐渐平滑趋于平坦块。

显然，对于整幅图像，模糊图像的稀疏表示误差更小，直接对整幅图像利用稀疏表示先验使目标函数的解偏向于模糊图像而不是清晰图像。图2（a）显示了清晰图像稀疏表示误差小于模糊图像稀疏表示误差的区域，将该区域表示为Rc=由于纹理块是指灰度变化明显的图像块，通常图像块的尺寸很小，图像块的灰度变化基本上等效于邻域内的灰度变化，因此，纹理块实际上与图像边缘的位置基本一致。图2（b）和图2（c）分别为清晰图像和模糊图像的边缘图像，模糊平滑了小尺寸结构，因而在模糊图像中检测不出小尺寸目标的边缘，并且小尺寸结构的边缘也不利于模糊核的估计［17］。然而，模糊使大尺寸结构的边缘变宽，使边缘加宽的部分对应的纹理块的稀疏表示误差更大，通过比较图2（a）和图2（c）可以看出，区域Rc与模糊图像边缘加宽的部分一致，仅在边缘周围清晰图像的稀疏表示误差小于模糊图像的稀疏表示误差。因此，本文仅对图像中的纹理块进行稀疏表示正则化约束，使重建图像偏向于清晰图像。

图2 清晰图像稀疏表示误差小于模糊图像稀疏表示误差的区域以及解释Fig.2 Area where the sparse representation error from the sharp image is less than that from the blurred image and its explanation

由于仅在纹理块上，清晰图像的稀疏表示误差小于模糊图像的稀疏表示误差，且图像降采样过程减弱图像的模糊程度，使图像块中的边缘更清晰。因此，本文提出了一种跨尺度字典学习的稀疏表示先验，该先验模型如下所示：

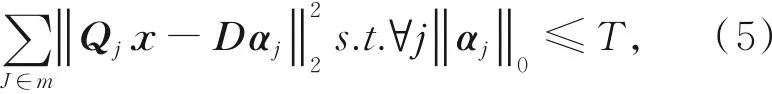
其中：M为二值标记矩阵，用于标记纹理块的位置，j∈M表示将本文提出的基于跨尺度字典学习的稀疏表示先验限制在标记矩阵M中值为1的纹理块。采用模糊图像的降采样图像作为字典学习的训练样本，将跨尺度自相似性引入字典学习中，并且仅作用于图像中的纹理块，使稀疏表示重建图像偏向清晰图像。

3 基于跨尺度字典学习的图像盲解卷积算法

在上一节提出的跨尺度字典学习的稀疏表示先验模型基础上，本节给出了本文提出的盲解卷积算法的数学模型及其求解过程。

3.1 图像盲解卷积数学模型

本文将跨尺度自相似性引入稀疏表示框架中，利用跨尺度字典学习的稀疏表示先验作为正则化约束，提出的单幅图像盲解卷积算法可表示为如下约束最优化问题：

其中：y为模糊图像，x为清晰图像，h为模糊核，∇={∂x，∂y}为图像梯度算子，*表示卷积操作，D为自适应字典为M中非零元素的个数，λc，λg，λh为正则化参数。式（6）中第一项为数据保真项，保证复原结果符合图像的降质模型；第二项为跨尺度字典学习稀疏表示正则项，迫使重建图像接近清晰图像；第三项为梯度约束项，利用L2范数对图像梯度进行约束保证图像边缘的平滑性；第四项为模糊核的正则化约束项，保证了模糊核的平滑性。

3.2 数学模型求解

为了加快算法收敛速度，以及大尺寸模糊核的处理，与目前大部分算法相同，本文通过构建图像金字塔模型由粗到细地估计清晰图像和模糊核。本文在通过图像金字塔逐层估计清晰图像和模糊核的过程中，直接将图像金字塔上一层估计的清晰图像结果作为当前层稀疏表示字典的训练样本，利用K-SVD算法生成过完备字典。由于式（6）所示的目标函数是非凸的，没有闭合解，本文在金字塔的每一层上采用交替迭代求解的方法对式（6）进行求解，即固定清晰图像的估计x^k，求解模糊核h^k+1，再固定模糊核h^k+1，更新清晰图像的估计x^k+1。每一次迭代，利用清晰图像的估计x^k+1更新标记矩阵M，通过对图像块进行筛选，排除平坦块对估计模糊核的影响。

3.2.1 筛选图像块

对当前估计的清晰图像x^k进行边缘检测，本文利用Sun等［18］的边缘检测算法确定当前估计清晰图像x^k中的边缘像素，边缘像素对应的图像块即为纹理块，参与模糊核的估计。引入二值矩阵M用于标记图像中的边缘像素，若当前估计的清晰图像x^k中某一像素为边缘像素，则将M中该位置的元素赋值为1，否则赋值为0。由于本文仅将稀疏表示正则项限制在图像的纹理块，导致当前估计的图像x^k中平坦块受到的约束较少，从而可能导致复原图像的平滑区域含有较多的噪声。为了减小噪声对边缘估计造成的干扰，本文首先对当前估计的图像x^k进行高斯滤波，然后对滤波后的图像进行边缘估计。

3.2.2 估计模糊核

对模糊核进行更新，即固定x^k，更新h^k+1，此时目标函数简化为：

其中：⊙表示逐元素相乘，二值标记矩阵M保证了在估计模糊核时，仅利用纹理块，避免了平坦块对模糊核估计的影响。这是因为图像中并不是所有的图像块都能为图像复原提供有效的附加信息。纹理块对模糊核的估计起着关键的作用，而平坦块对模糊核估计几乎不起作用，例如若某一图像区域的像素值为常数，则该区域经过模糊后的像素值仍为同一常数，在该区域清晰图像与模糊图像完全相同，因此这一区域并不能为模糊核的估计提供有效的信息。

式（7）为关于h的二次函数，因此存在闭合解，令式（7）对h的导数为零，可得式（8），在式（8）中，⊙表示相关运算。根据卷积定理可知，空域中图像的卷积等效于傅里叶变换的频域乘积，本文将式（8）转换到频域求解，如式（9）所示。

由式（9）可得h的闭合解，式（10）给出了闭合解的表达式，在式（10）中，F(·)表示傅里叶变换，表示傅里叶逆变换表示傅里叶变化的复共轭。公式（8）～（10）如下所示：

3.2.3 估计清晰图像

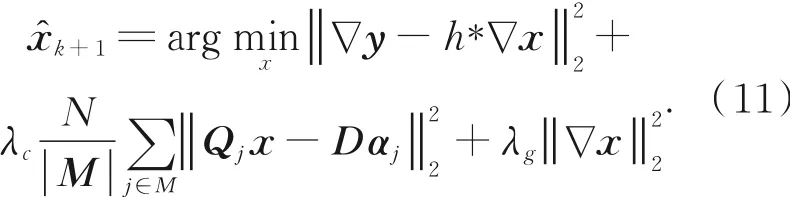
由于式（11）中的稀疏表示系数αj依赖于方程的解x^k+1，因此，该式没有闭合解。本文利用上一次对清晰图像的估计x^k近似x^k+1进行求解，对每一个图像块Qj x^k，利用OMP算法求解稀疏表示系数，即求解如下约束最优化问题：

通过对所有纹理块的重建图像块Dαj进行求和处理可得稀疏表示的重建图像，即：

本文直接使用图像金字塔上一层估计的清晰图像作为当前层稀疏表示字典的训练样本，通过K-SVD算法求解式（4）生成字典D。由于降采样版本的图像块边缘更加清晰，与清晰图像更加相似，将其作为训练样本获得的字典能够更好地对清晰图像进行稀疏表示，在该字典下仅对图像中的纹理块进行稀疏表示重建，能够使重建图像的边缘接近清晰图像的边缘。

将式（11）表示为矩阵向量乘积的形式，则有：

其中：Δx，Δy∈RN×N分别为梯度算子∂x，∂y的矩阵形式，Hk+1为模糊核矩阵。令式（14）对X的导数为零，可得如下方程：

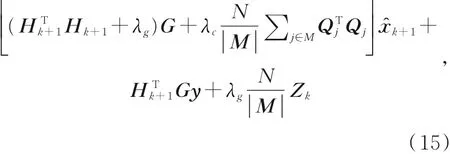
4 实验结果与分析

本文设置图像块的尺寸n=5×5，字典大小t=100，稀疏度约束T=4，由于真实模糊图像的模糊核尺寸一般小于51×51，参照文献［18］和文献［8］，若无特殊说明，本文实验中模糊核的尺寸设置为51×51。降采样因子a越小，降采样模糊图像中的图像块越清晰，但同时图像块的个数也越少，本文参照Michaeli等［8］将图像金字塔之间的降采样因子设置为4/3，在构建金字塔模型时，若当前层对应的模糊核尺寸小于3×3，则停止降采样的过程。

4.1 Kohler数据集实验

在Kohler数据集［19］的实验中，将本文的算法与Krishnan等［6］、Pan等［9］、Chang等［15］和Anger等［7］的算法进行比较。Kohler数据集［19］中的模糊图像是由真实记录的三维空间运动轨迹而合成的，包括4幅图像，12个运动轨迹，共生成48幅模糊图像。该数据集属于非均匀模糊，上述算法均利用线性卷积模型对非均匀模糊进行近似建模。为了公平比较，本文的算法也根据模糊程度的不同，将模糊核尺寸设置为51×51和151×151。Krishnan等［6］、Pan等［9］和Chang等［15］的结果是由作者本人提供，Anger等［7］的结果由作者提供的程序运行得到。

通过比较每一幅图像的去模糊结果与沿着相机运动轨迹捕获的199个未模糊图像的峰值信噪比（Peak Signal to Noise Ratio，PSNR），将PSNR的最大值作为定量评估的指标。复原图像与真值图像之间的PSNR越大，表明复原图像与真值图像越接近。

图3 为各个算法在Kohler数据集［19］上PSNR的均值与标准差，从图中可以看出，本文算法在四幅图像上的平均PSNR均高于Krishnan等［6］、Chang等［15］和Anger等［7］的结果，在后两幅图像上的平均PSNR高于Pan等［9］的结果。即使该数据集中的前3幅图像含有足够多的暗像素，符合Pan等［9］所提出的暗通道先验，本文的算法也达到了与Pan等［9］方法相当的结果。此外，从图中的垂直误差条可以看出，本文的算法在四幅图像上均取得了最小的标准差，从而说明本文的算法具有良好的鲁棒性。

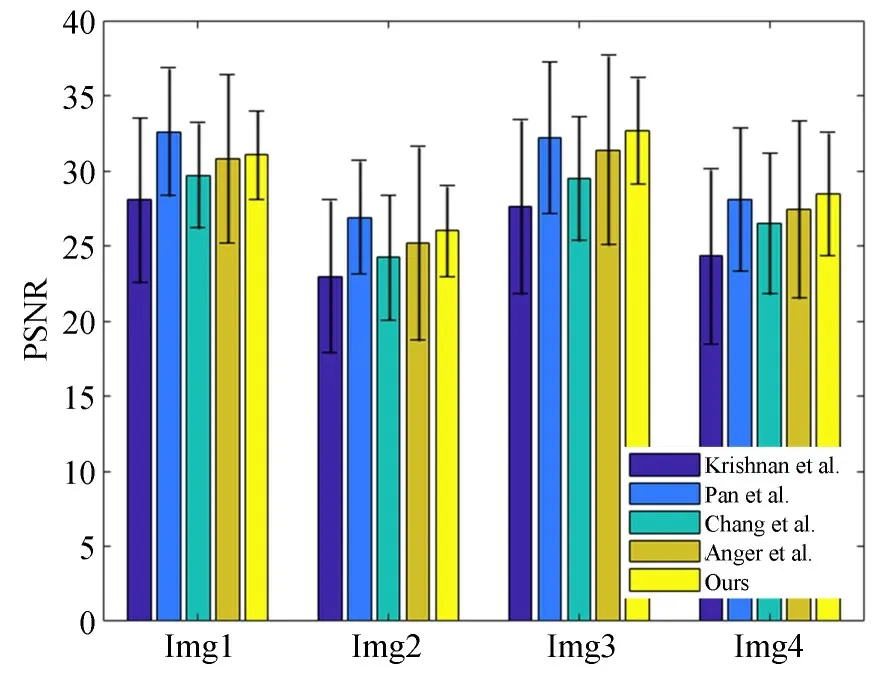
图3 Kohler数据集PSNR的平均值与标准差Fig.3 Mean and standard deviation of PSNR on Kohler et al.′s dataset

在Kohler数据集［19］中编号1～7、12为小幅度运动轨迹（对应小尺寸模糊核），编号8～11为大幅度运动轨迹（对应大尺寸模糊核），分别对于大尺寸模糊和小尺寸模糊这两种情形比较各个算法的复原结果。图4比较了各个算法对大尺寸模糊复原的PSNR均值与标准差，从图中可以看出，本文算法的平均PSNR明显高于Krishnan等［6］、Pan等［9］、Chang等［15］、Anger等［7］的结果。图5为各个算法对小尺寸模糊复原的PSNR均值与标准差，由图中可见，本文的算法在第四幅图像上取得了最高的平均PSNR；在前三幅图像上的平均PSNR高于Krishnan等［6］、Chang等［15］的结果。根据图4和图5给出的结果可见，本文的算法能够更好地解决大尺寸模糊核的复原，并且对于小尺寸模糊核也具有良好的复原效果和鲁棒性。

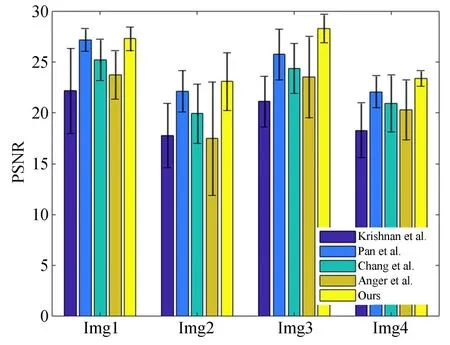
图4 Kohler数据集中编号8～11模糊对应的PSNR平均值与标准差Fig.4 Mean and standard deviation of PSNR on blur numbered 8-11 from Kohler et al.′s dataset

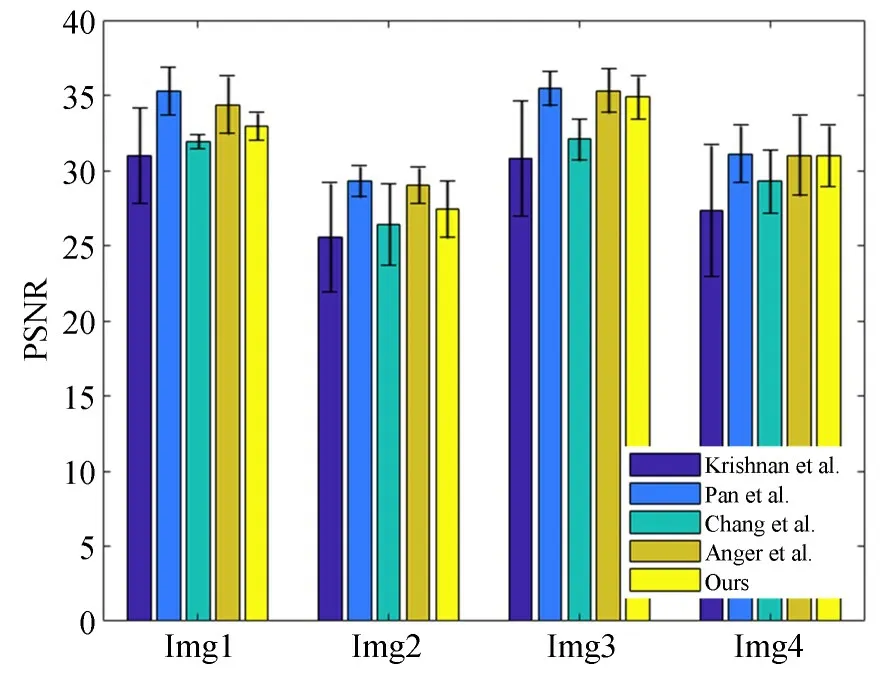
图5 Kohler数据集中编号1～7，12模糊对应的PSNR平均值与标准差Fig.5 Mean and standard deviation of PSNR on blur numbered 1-7 and 12 from Kohler et al.′s dataset

图6 各个算法对Kohler数据集中一幅大模糊图像复原结果的比较Fig.6 Comparison of the results deblurred by various state-of-the-art methods on a severely blurred image from Kohler et al.′s dataset

图6 比较了各个算法对Kohler数据集［19］中一幅大模糊图像的复原结果，在每幅图像的左上角为各个算法估计的模糊核。图6（a）为模糊图像，图6（b）～（f）为Krishnan等［6］、Pan等［9］、Chang等［15］、Anger等［7］以及本文的算法对图6（a）的复原结果，它们与真值图像的PSNR分别为22.75，22.30，22.94，21.57和29.90。本文的算法达到最高的PSNR，估计出更准确的模糊核，从而复原结果更接近真值图像。

4.2 真实模糊图像实验

在真实模糊图像实验中，将本文的算法与Yan等［10］、Chang等［15］、Chen等［11］以及Anger等［7］的算法进行比较。Yan等［10］、Chen等［11］和Anger等［7］的复原结果是由作者提供的程序运行得到，Chang等［12］的复原结果由作者直接提供。由于真实模糊图像一般为非均匀模糊，上述算法均利用线性卷积模型近似建模非均匀模糊。

图7 和图8比较了各个算法对两幅真实模糊图像的复原结果，图（a）为模糊图像，图（b）～（f）为Yan等［10］、Chang等［15］、Chen等［11］、Anger等［7］以及本文算法的复原结果，在每幅图像的左上角为各个算法估计的模糊核，下方为图像中局部区域的细节放大图。从各个算法对图7（a）的复原结果和细节放大图可以看出，本文的算法能够复原出更清晰的边缘和细节，同时减小了振铃效应。图8（a）为低光照环境中获取的真实图像，当光线不充足时图像容易产生噪声，从各个算法的复原结果和细节放大图可以看出，Yan等［10］、Chang等［15］和Anger等［7］的复原结果均放大了噪声并且存在明显的振铃效应，Chen等［11］减小了振铃效应，但仍存在噪声放大的情况，本文的算法能够有效地抑制振铃效应以及噪声，具有良好的鲁棒性。

图7 各个算法对一幅真实模糊图像复原结果的比较Fig.7 Visual comparison with various state-of-the-art methods on one real-world photo

图8 各个算法对另一幅真实模糊图像复原结果的比较Fig.8 Visual comparison with various state-of-the-art methods on another real-world photo

5 结 论

本文提出了一种基于跨尺度字典学习的稀疏表示先验模型，将降采样模糊图像作为字典的训练样本，并在该字典下对图像中的纹理块构造稀疏表示正则化约束项，加入图像盲解卷积的目标函数中，使目标函数的解偏向于清晰图像。同时，在金字塔的逐层迭代中，将上一层估计的清晰图像作为当前层稀疏表示字典的训练样本，在该字典下对图像中的纹理块进行稀疏表示，进一步减小稀疏表示误差，使当前估计的图像更加接近清晰图像。本文算法在Kohler数据集上复原结果的平均峰值信噪比为29.54 dB。大量模糊图像上的实验验证了本文算法的有效性和鲁棒性。