组合曝光的计算成像系统及其复原

吴笑天，吕 博，刘 博，杨 航

（1.长春理工大学光电工程学院，吉林长春130022；2.中国科学院长春光学精密机械及物理研究所，吉林长春130022）

1 引 言

传统的光学成像系统往往采用成像链路各个环节分离化的设计思路，其光学设计、传感器驱动及面向任务的图像处理都在局部范围内优化。这种设计方式能够满足消费类及部分低成像分辨率应用场合的要求，但是无法满足高端工业及军工领域对于高分辨率、高灵敏度、多维信息融合等特种应用需求，传统的成像设计方式不再适用。因此，一种面向任务需求的全成像链路环节定向定制、全局优化的成像方式应运而生，即计算成像。计算成像是几何光学、波动光学、电子学和信息科学等学科的交叉融合，近年来备受学术界和产业界的关注。

计算成像系统在设计理念上强调面向任务背景需求的全局定制化设计。由于任务的多样性，计算成像主要包括孔径编码、全息成像、光场成像、压缩感知、计算鬼成像和散射介质成像等方法［1-2］。其中，单光子成像和计算鬼成像主要应用于远红外成像、深紫外成像和极弱光成像背景下的高空间采样率成像［1］。其主要机理在于光的二阶相干性。最早的单像素成像利用纠缠光子对的空间信息实现目标空间信息的探测［3］，而后发展的计算鬼成像则利用空间光调制器模拟光子的随机性，采用单一像素探测器实现“单像素级”成像［4］。但是，无论单像素成像、计算鬼成像，还是后期进一步发展的对偶摄影［5］，都需要对场景进行多次投影采集（需要上万次甚至更多）。虽然它们可以在极其微弱的成像条件下使用，却难以实现动态目标的成像［1］。张玉叶等［6］提出了一种基于多设备多曝光图像融合的计算成像方式，但是该方式除了增加系统成本之外，成像效果也易受多采集源配准精度的影响。弱光环境下的常规成像可以通过构建深度学习网络模型实现细节的显著增强，Chen等［7］通过对大量场景采集长短曝光图像形成数据库用于神经网络的训练，训练后的神经网络可以将弱光条件下拍摄的低对比图像恢复为细节纹理清晰的正常图像。该方法仅在训练段使用了长短曝光的信息融合以形成训练数据集，而在实施阶段没有用到长积分图像的信息，因此可以理解为低照度条件下的图像去噪及增强问题。

模糊图像复原是计算成像方法的核心问题之一，直接决定并影响着系统最终的成像效果［8］。在传统图像处理领域，图像复原算法虽然与成像链路的其他环节分离化设计［9-10］，但是许多方法依然对计算成像系统的实施具有借鉴和指导意义。近年来，围绕图像复原问题的研究主要包括两类理论实现方式：基于优化框架的复原方法和基于深度学习的复原方法。基于优化框架的复原方法属于一种物理模型驱动的理论方法。由于图像复原问题是一个典型的病态问题，基于优化框架的复原方法通常需要添加先验约束并整合进优化理论框架中，以使病态问题具有可解性。这些优化先验方法主要包括L0梯度［11］、梯度稀疏性［12-13］、暗通道［14］等。所采取的优化框架主要包括边缘化法（Marginalization Approach，MA）和最大后验概率法（Maximum A Posteriori，MAP）。Pan等［14］利用暗通道的稀疏性提出一种求取暗通道的线性化方法以代替原有暗通道的求取，从而规避了原有暗通道非凸非线性对于优化框架的影响，取得了较好的复原效果，并且适用于非均匀一致的盲复原效果。Whyte等［15］建立了相机拍摄随机抖动的数学模型，并利用高速运动去模糊［16］的方法实现了非均匀一致的图像复原。基于深度学习的图像复原方式属于一种数据驱动型的理论方法，不同的数据驱动推断的切入点及实现方式各有不同。Chakrabarti［17］等利用一种深度学习网络实现模糊核傅里叶系数的估算；Li等［18］将神经网络训练用于MAP模型框架下的先验信息，取得了良好的效果；Nah等［19］提出了一种多尺度卷积神经网络，以端到端的方式实现模糊图像的清晰化复原；Zhang等将循环神经网络（Recurrent Neural Network,RNN）的特征提取优势与卷积神经网络（Convolutional Neural Network,CNN）的权重学习特性相结合，实现了一种可用于非均匀运动模糊复原的神经网络［20］。近年来，随着生成对抗网络（GAN）的不断发展，忽略物理模型过程直接端到端生成复原图像的实现方式也被应用在图像去模糊领域［21］。然而，上述论文均为基于单帧图像的去模糊复原方法。Yuan和Lee［22-23］等研究了基于多帧图像的模糊复原方法，利用边缘清晰帧的梯度信息实现了模糊帧的图像复原。

针对低照度环境下高速运动物体的清晰成像问题，传统成像方式难以通过积分时间的配置达到预期的效果，其原因在于低照度环境下，在孔径光阑达到极限设计时，依然需要长积分时间获取足够的光通量以达到高信噪比成像的要求。但是长积分时间会导致高速运动物体模糊，进而影响后续的成像效果。

本文提出一种基于组合曝光的计算成像方式，在成像链路环节上将传感器驱动设计与面向任务的图像处理环节合并优化。为了实现组合曝光图像对的信息互补应用，采用一种基于EFF（Efficient Filter Flow）框架下由粗至精的全局非一致运动模糊核点扩散函数（Point Spread Function，PSF）求解方法，在求解过程中利用短积分时间的梯度信息和长积分时间的像素信息共同辅助模糊核的求解，最后利用全变分（Total Variation，TV）框架下的快速算法复原出高质量的清晰图像。该方法能够满足低照度环境下高速运动物体的清晰成像需求，计算成像结果清晰，具有良好的主观视觉效果。

2 成像原理及图像复原模型

面向低照度微光条件下的高速目标运动成像问题，本文提出的计算成像方式需要将传感器设计和图像处理结合，形成面向任务需求的联合优化。因此，其成像方式的实现主要包括传感器及硬件平台和匹配的图像复原算法两部分的设计。

2.1 传感器及硬件平台的设计

传感器及硬件平台作为组合曝光计算成像的重要组成部分，需要定向定制，以实现特殊的组合曝光时序设计。

为了满足低照度高灵敏成像及后续计算合成的需求，需要在高灵敏度（像元尺寸及量子转化效率）和高帧频（上限帧频范围）之间权衡。经过调研，本文选择长光辰芯公司生产的GSENSE2020作为本系统的主传感器，其主要性能指标如表1所示。相机的后端处理电路主芯片为Xilinx公司的K7系列芯片XC7K325T，输出接口为标准Camlink-Full，相机系统样机如图1所示。

图1 计算成像相机系统Fig.1 Computational imaging camera system

表1 GSENSE2020的主要性能指标Tab.1 Main indicators of GSENSE2020

该芯片在使用时具有正常高帧频模式和长短组合曝光模式两种工作模式，如图2所示。

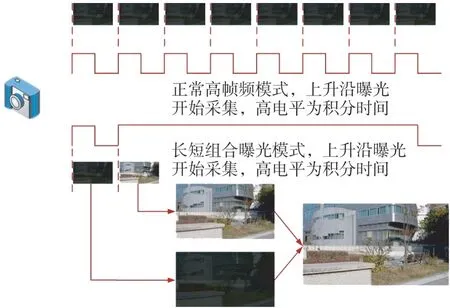
图2 相机工作模式示意图Fig.2 Schematic diagram of camera operation modes

正常高帧频模式下，相机处于标定状态，如图2所示，此模式用于测量摄影高速物体所需的最短积分时间；在低照度环境下，积分时间与信噪比成反比。这里利用一种无参考图像量化函数评价图像的信噪比数值，以确定最低的积分时间配置，如式（1）所示：

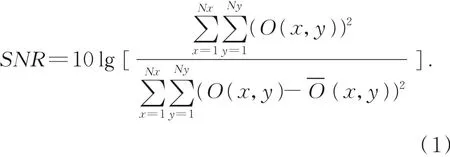
经过试验，下限信噪比数值设置为6 dB，以此确定系统的最低积分时间，上限不可超过高帧频相机可接受的最大积分时间，在500 frame/s的模式下，积分时间最大可设置为2 ms。

长短组合曝光模式是系统正常的工作模式，长积分时间的设置需要综合考虑高速运动物体在物方的空间分辨率、最大运行速度及成像系统焦距等信息，如图3所示。

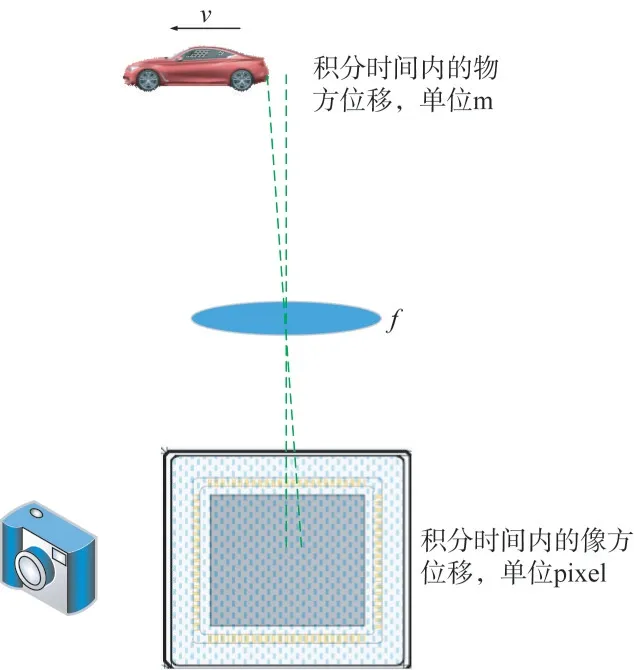
图3 积分时间内的像移产生Fig.3 Image shift in integral time

2.2 图像复原模型

本文的核心目的在于实现长积分时间观测图像的复原，其成像模型表述如下：

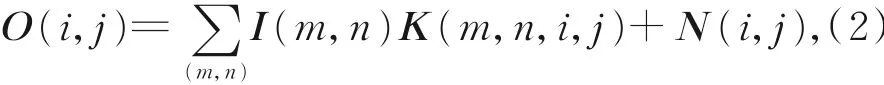
式中：O（i，j）为成像系统采集的长积分时间观测图像，（i，j）为观测图像空间的像素位置；I（m，n）为真值图像，（m，n）为真值图像空间的像素位置；K（m，n，i，j）为运动模糊SPF；N（i，j）为成像噪声。由于高速运动物体的运动速度与背景明显不一致，因此运动模糊SPF既与观测图像的像素空间位置有关，又与真值图像的像素空间位置有关，K（m，n，i，j）表征了该全局非一致性。

虽然长短曝光的图像对存在双输入源，即长积分时间图像O（i，j）和短积分时间图像O^(i，j)，但是图像复原的直接目标仅在于实现长积分时间图像O（i，j）的复原，而短积分时间图像O^(i，j)由于信噪比的原因仅在模糊核估算阶段提供额外的边缘信息，不作为复原目标图像呈现在式（2）中。因此在式（2）中，已知观测的模糊O（i，j），未知真值图像I（m，n），运动模糊SPFK（m，n，i，j）及成像噪声N（i，j）。上述问题在数学上为典型的病态问题，本文采用基于优化框架的复原方法，需要添加先验约束并整合进优化理论框架中，以使病态问题有解。

3 图像复原算法

图像复原是计算成像系统的核心部分，计算复原的输出直接决定并影响着系统成像的最终成像效果。为了适配组合曝光成像采集模式，克服高速运动物体在成像背景中形成的非均匀一致运动模糊，合理利用长短积分时间图像。本文提出了一种改进式EFF框架的全局非一致运动模糊核的估计算法及全变分框架下的快速复原算法。其中，EFF框架的全局非一致运动模糊核的估计算法主体借鉴了Whyte等［15］所使用的方法及文献［16］的部分思路。模糊核迭代方法是在EFF框架下实施的，该框架由Hirsch等［24］提出，用于非一致去模糊的各种场合［15，26］。在EFF框架下实施迭代及复原的过程，能够切合本系统非均匀一致运动模糊的特点。同时，本文对模糊迭代方法进行了一定的改进，使用短积分时间图像和长积分时间图像联合实施模糊求解，以期获得更为精确的模糊核估计。

3.1 模糊核的迭代估计

如图4所示，图像复原过程从整体上划分为两个部分：模糊核的迭代估计和已知估计模糊核的非盲图像复原。模糊核迭代估计的具体实施步骤主要包括由低至高的迭代实施预处理、模糊核和真值图像之间的交替估算。预处理及模糊核估计分别使用了短积分时间图像和长积分时间图像。

在EFF框架下，尺度由粗至精的实施，对于本文1 280×720分辨率的图像，尺度为9级，每一级尺度的PSF的初始估计由上一次尺度的上采样获取。每一个尺度内的迭代实施实质相当于低精度的完整图像复原过程，区别仅在于复原解卷积不需要高质量的图像输出。尺度由低至高的实施意义在于提升运算效率。每一个尺度内的迭代复原不需要较高的精度，本文设置为5次，最高尺度的最后一次为最终的非均匀一致的模糊核估计，非盲图像复原的输入。

3.1.1 预处理

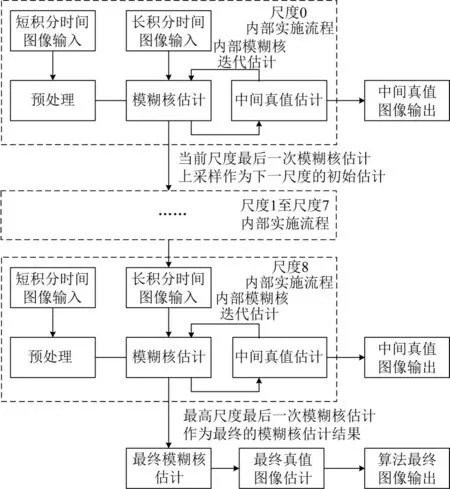
图4 模糊核估计流程Fig.4 Flow chart of kernel iterative estimation

预处理的意义在于获取强边缘图像，而短积分图像包含清晰的强边缘纹理信息，使用该图像作为预处理的输入更为合理。同时，由于短积分时间的信噪比比较低，需要双边滤波、冲击滤波和梯度提取3个子过程串联实施，以便求解保留强边缘的梯度图像

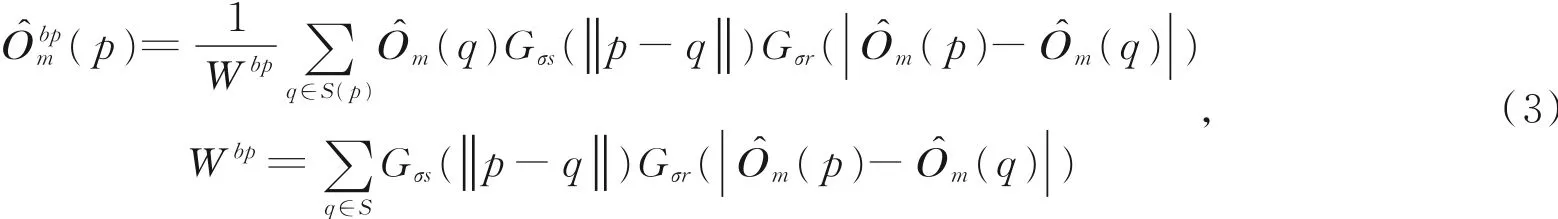
冲击滤波［25］和边缘阈值提取操作用于提炼强梯度图像用FuncShoGrThred来代表这一过程，即有：

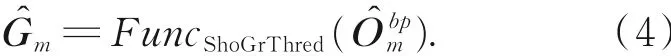
3.1.2 模糊核的交替估算

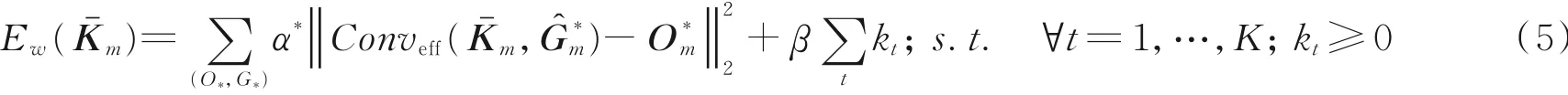
式中Conveff代表着解卷积操作在EFF框架下实施的为L1范数正则化项代表了不同方向的偏微分操作，α*为权系数为当前迭代次数的模糊核估计。该目标函数的意义在于让强梯度图像与模糊核估计卷积后更接近于长积分图像

3.1.3 真值图像的交替估算

在迭代运算中，真值图像的估算主要用于监测反馈模糊核的估计效果。在已知模糊核估计基础上，优化目标函数如下：

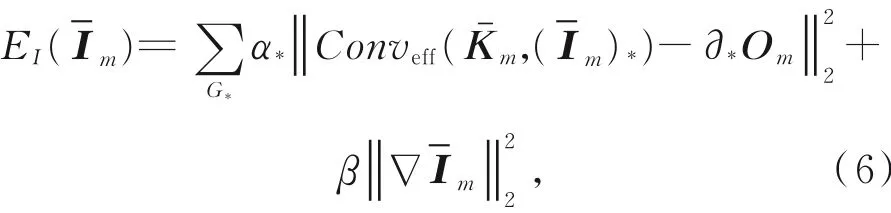
式中∂*∈{∂0，∂x，∂y，∂xx′，∂xy′，∂yy}代表不同方向不同阶次的偏导算子，α*为其系数，β为正则化项的权系数。

上述迭代实施过程的中间结果如图5所示。

图5 模糊核迭代估计中的中间试验结果Fig.5 Intermediate test results in fuzzy kernel iterative estimation

3.2 非盲图像的最终复原

在经过迭代并最终获得非均匀一致的模糊核估计Kˉfinal的基础上，选择常规的非盲图像复原算法来实现这一过程。本文选用全变分框架下的快速算法［27］来完成复原工作，该方法能较好地复原图像的边缘轮廓。

全变差复原模型为：

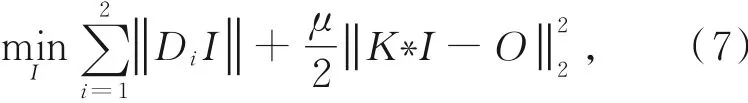
其中D1和D2分别表示对x和y方向的偏导算子。在已知SPFK的情况下，论文［24］采用分离变量法，引入中间变量wi（i=1，2）求解上述最小化问题，如式（8）所示：

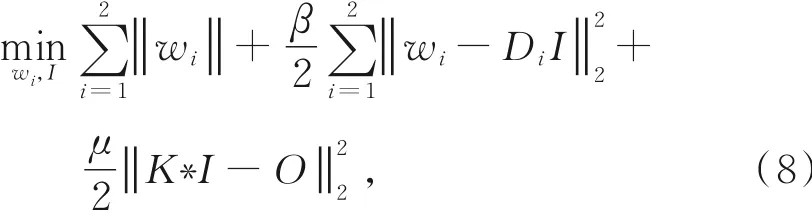
其中β是一个充分大的正数。这一优化问题的优点是，当两个变量I和w中的任何一个是固定值时，相对于另一个变量最优化问题具有低计算复杂度和高数值稳定性的闭式公式。

4 试 验

4.1 系统实现及实测图像复原效果

使用2.1所述的计算成像样机硬件系统，本文方法的复原效果如图6所示。系统测试在10 Lux的光照环境下进行，短积分时间设置为100 us，拍摄效果如图6（a）所示；长积分时间为4 ms，可见运动模糊，如图6（b）所示；使用本文方法获得的复原图像为图6（c）所示；模糊及复原图像细节对比如图6（d）和6（e）所示。

图6 计算成像相机的成像效果Fig.6 Images captured by computational imaging camera

4.2 仿真试验结果

Nah等［19］发布了一个开源数据集，该数据集使用GOPRO4相机以240 frame/s的帧率在自然场景中随机拍摄高速的连续图片序列，并从图片序列中构建配对的真值图像序列和模糊图像序列。其中，模糊图像序列的构建基于真值图像临近7～13帧随机产生。该数据集为非均匀一致运动模糊提供了可供真值参考的依据，后续相关方法［20-21］均基于该数据集实现算法的评估与验证。

本文基于该开源数据库进行算法仿真。模糊图像直接采用该数据集发布的图片，然后将真值图像灰度降低5倍并叠加均值灰度为20的高斯噪声模拟低照度短积分图像。本文方法的试验效果如图7所示。

图7 分步试验效果Fig.7 Step-by-step experimental results

由图7可知，虽然短积分图像的信噪比较低，但是短积分图像仅在PSF的迭代阶段提供边缘信息，且边缘信息使用前采用了式（3）所示的双边滤波和式（4）所示的冲击滤波及梯度提取手段执行预处理，很大程度上抑制了噪声对图像边缘获取的影响。因此，经过该短积分图像的辅助所获取的全局非一致的运动模糊PSF较为精确，主要表现在复原结果清晰可靠，无明显图像振铃现象，具有良好的主观视觉效果。

其他图像的复原效果如图8所示。从图中可以看出，本文所述的图像复原算法能够利用长短积分时间图像的信息获得较好的全局非一致运动模糊PSF估计，进而实现清晰的图像复原效果。

4.3 与其他图像复原方法的对比

同样基于该GOPRO数据库，本文对比了基于优化方法的L0 Sparse［11］方法，Dark Channel［14］方法和基于深度学习的Deep Multi-scale［19］和RNN+CNN［20］方法，客观评价指标选取了图像复原领域常用的峰值信噪比（Peak Signal to Noise Ratio，PSNR）和结构相似指数（Structural Similarity Index Measure，SSIM），指标评价结果如表2所示。图像复原效果对比试验结果如图8所示，截取若干细节图块进行对比，如图9所示。

上述数据及试验结果表明，本文方法能够有效抑制运动模糊，图像纹理细节得到了明显的改善且无明显振铃效果，客观评价指标PSNR、SSIM较比原始降质图像提升10%左右，整体性能指标优于现有的非深度学习方法。对比表2中列举的几种图像复原理论方法，本文方法在客观指标评价及视觉细节的恢复上明显优于L0 Sparse方法；Dark Channel在客观评价指标PSNR上与本文方法接近，但在SSIM指标上本文方法更优。此外，该文所述方法在细节恢复上产生较多的振铃效果，这是由于Dark Channel先验在模糊复原优化框架中，尤其在全局非一致的模糊图像复原使用中并不十分理想，PSF估计并不准确，而这种振铃的复原效果在PSNR评价指标中往往不能体现，而在SSIM指标中能够有所体现；Deep Multi-scale法［19］在客观评价指标及主观复原效果与本文所述方法接近，但也丢失了一些细节信息。RNN+CNN法［20］在客观评价指标及主观视觉效果略优于本文方法，但仔细观察会发现，在局部区域没有完全去除模糊效果。

这里需要指出的是：Deep Multi-scale法和RNN+CNN法属于深度学习理论方法，即基于数据驱动型的图像复原方法，在实际使用中往往需要执行先期的数据预训练才能够部署使用，同时受到深度学习方法泛化能力的限制，往往不能在光照及其他场景环境发生变化时稳定地实现各类场景的清晰化复原。

图8 不同图像复原方法的试验对比Fig.8 Experimental comparison of different image restoration methods

图9 不同图像复原方法的试验对比。第一列为长积分时间模糊图像；第二列为短积分时间低信噪比图像；第三列为L0稀疏表示的复原结果；第四列为暗通道法的复原结果；第五列为深度多尺度变换的复原结果；第六列为RNN与CNN的复原结果；第七列为本文复原结果；第八列为真值图像Fig.9 Experimental comparison of different image restoration methods.The first column is a long integral time blur image；the second column is the image with short integration time and low SNR；The third column is the recovery result of L0 sparse;the fourth column is the recovery result of dark channel;the fifth column is the recovery result of deep multi-scale;the sixth column is the recovery result of RNN+CNN；the seventh column is the recovery result of this paper；and the eighth column is the true value image

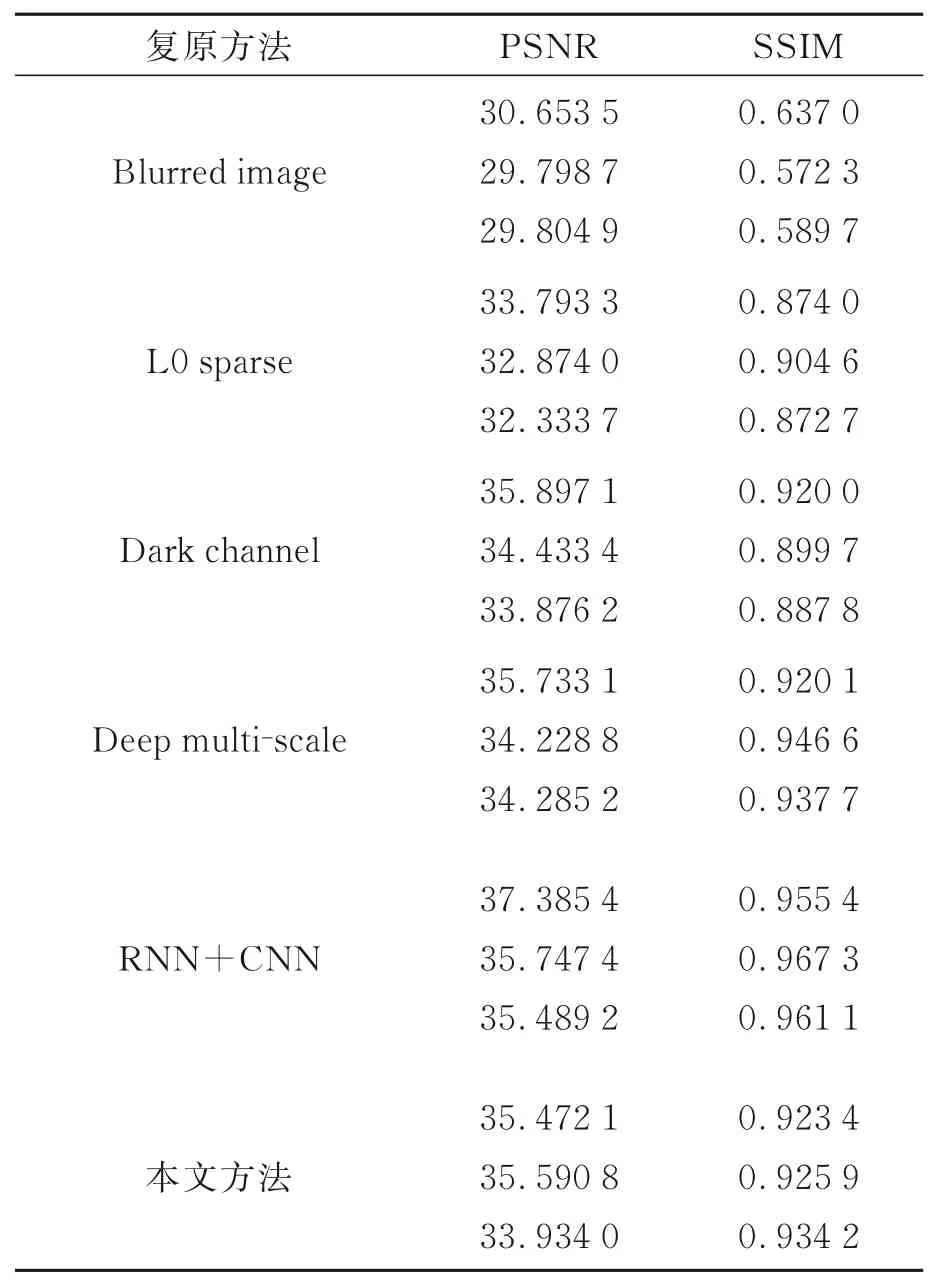
表2 不同图像复原方法的PSNR/SSIM指标对比Tab.2 Comparison of PSNR/SSIM indexes among different restoration methods

5 结 论

本文针对低照度条件下高速运动物体的摄影成像，提出一种基于计算成像的设计思路，在成像链路环节上将传感器设计和图像处理设计两个环节联合设计，提出一种基于长短组合曝光的计算成像方式及图像复原算法。试验结果表明，该计算成像方法能够有效解决传统成像方式下能量获取和高速运动模糊之间的矛盾，所采集的图像复原算法能够有效抑制运动模糊，在图像纹理细节上有明显的改善且无明显振铃，客观评价指标PSNR、SSIM较比原始降质图像提升10%左右，整体性能指标优于现有的非深度学习方法。该方法复原的图像纹理清晰，具有良好的主观视觉效果。

计算成像强调成像链路环节的全局优化，本文在成像链路环节上选取了传感器设计和图像处理两个环节展开联合设计，并获得了较好的复原结果。在光学设计中，孔径光阑和轴外像差是一对矛盾体，但轴外像差校正同样可以结合图像复原处理［26，28］形成另一个思路的优化设计。因此，后续工作是将光学设计环节的优化融合进本计算成像链路框架中，以期进一步扩展低照度条件下高速摄影成像设备的动态范围，实现光学设计、传感器设计和图像处理三者联合的全局优化。