结合天空分割和透射率映射的图像去雾

杨 燕，张浩文，张金龙

（兰州交通大学电子与信息工程学院，甘肃兰州730070）

1 引 言

在雾霾条件的场景下，由成像设备获得的图像存在细节丢失、对比度和能见度下降等问题，尤其在景深区域更加严重，这是由于大气中大量微小颗粒对光线的吸收和散射作用导致的。这对计算机视觉应用造成了困难，例如户外监控系统、目标跟踪以及场景分析等。有效的图像去雾算法对于计算机视觉系统更好地运行具有重要意义。

针对图像去雾提出的众多方法中，目前主要分为两大类：传统的基于图像效果算法和基于深度学习的算法，其中基于图像效果的算法可分为基于图像增强的算法［1-2］和基于图像复原的算法［3-5］。其中基于图像增强算法的基本思想是突出图像的某些信息从而达到图像增强的效果，由于不考虑图像退化的原因，恢复图像往往不太自然。基于图像复原的算法是通过分析图像降质的本质，建立大气散射模型，利用一些先验知识或假设，估计散射模型中的必要参数，再通过散射模型反推出无雾图像。基于图像复原的算法往往可以实现较自然的去雾效果，是图像去雾研究的热点方向。基于深度学习的算法往往需要大量的样本训练，由于目前没有大量真实的有雾图像数据集，用于训练的都是经过合成的有雾图像数据集，所以恢复图像存在缺陷［6-10］。

近年来，基于先验知识或者假设的单幅图像复原去雾算法获得重大突破。这类方法的注意力在于对大气光值和透射率的估计。对于大气光值的估计，应尽可能地依靠天空区域的像素值。He等［11］利用暗通道中0.1%最亮像素点对应原图的像素值对大气光值进行估计，很容易受图像中白色物体的影响，导致大气光值估计不准确。Kim等［1］利用四叉树的方法估计大气光值，可以避免小块白色物体对大气光估计的影响，但是当图像中存在大片白色区域的时候就会失效。Wang等［12］利用灰度投影的方法估计大气光，同样受大片白色区域的影响。对于透射率的估计，基于不同的先验知识和假设，提出了很多估计透射率的方法。Zhu等［13］利用颜色衰减先验，通过景深和亮度、对比度的关系估计透射率，该方法不能自适应地调整参数，导致透射率估计不准确，恢复图像往往留有残雾。Kumar等［14］利用颜色一致性原则估计透射率，该方法虽简单有效，但估计的透射率可能整体偏大或偏小，导致过度去雾或去雾不彻底。He等［11］提出了暗通道先验理论估计透射率，但是在大片天空区域和高亮区域仍失效。

对于含有天空区域的图像，以上方法对天空区域的处理都容易产生失真现象。本文首先对天空区域进行分割，在天空区域进行大气光值的估计，结合超像素分割改进暗通道有效地削弱halo效应，然后对天空和非天空区域进行不同的透射率映射得到最终的透射率。对于不含天空和只含天空图像的图像，本文也可以自适应地处理。相比传统暗通道先验理论，本文算法有效地解决了传统暗通道先验理论在大片天空区域和高亮区域失效的缺陷，相比其他基于天空区域分割的去雾算法，本文算法有效地解决了因分割错误在分割边界处可能出现的问题，通过实验观察发现，本文算法在天空区域和非天空区域均表现出色。

2 背 景

2.1 大气散射模型

根据大气散射模型［15］，获得的有雾图像可以表示为：

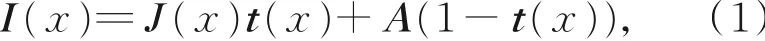
其中：x为像素坐标，I(x)为有雾图像，J(x)为无雾图像，A为大气光值，t(x)为透射率。基于式（1）的有雾图像复原过程其实就是已知有雾图像I(x)，通过估计大气光值A和透射率t(x)，从而还原无雾图像J(x)的过程。当大气中引起图像降质的颗粒介质均匀分布时，透射率t(x)可以表示为：

其中：β为散射系数，d(x)为场景深度。

2.2 暗原色先验

根据暗原色先验理论［11］，在大多数非天空区域内，至少有一个颜色通道在局部区域趋近于0，即：

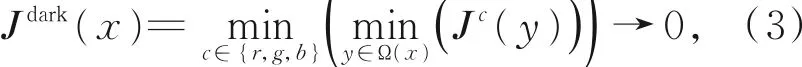
其中：Jc表示J的三个颜色通道，Ω(x)表示窗口尺寸为n×n的以x为坐标中心的局部区域内像素点集合，Jdark为暗通道图像。

对式（1）左右两边同时作暗通道操作，并将式（3）的假设代入，可得透射率为：

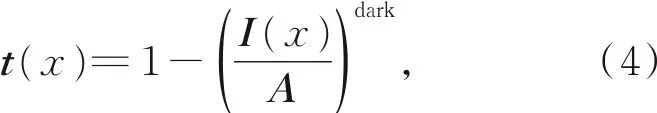
其中dark表示式（3）中类似的暗通道操作。为了保留一定残雾，改善恢复无雾图像的表现效果，文献［11］引入一个调整因子ω=0.95，故式（4）被进一步写为：

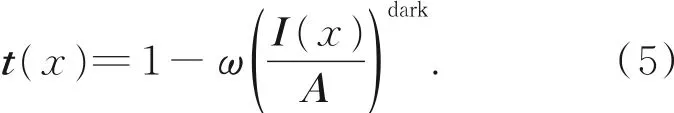
只要得到透射率t(x)和大气光值A的估计，利用式（1）可以推导出复原去雾图像的公式：

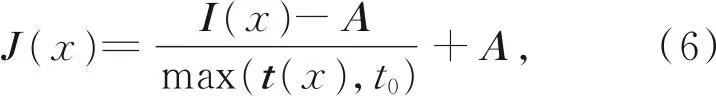
其中t0是人为设置的透射率t(x)的下界，通常取0.1。

3 本文算法

3.1 算法原理

算法原理框图见图1，首先由最小值通道图像粗略分割图像天空区域，在粗略分割后的天空区域对应原图像素值求平均得到大气光值A。再结合超像素分割和最小值通道以及大气光值A得到初始透射率，进行导向滤波操作得到细化透射率。对细化透射率进行直方图自适应分析，若95%的像素值小于0.5，则判断图像只含天空，对细化透射率利用天空透射率映射方法得到最终透射率，并结合大气光值A恢复无雾图像。否则便求得天空区域分割阈值Tt，或者判断图像为不含天空图像。对于含天空图像，利用阈值Tt精细分割天空区域，对不同的区域应用不同的透射率映射关系得最终透射率。对于不含天空图像，将超像素改进暗通道中最亮0.1%像素点对应原图中的像素值求平均作为大气光值，应用非天空区域透射率映射关系求得最终透射率。最后由大气散射模型恢复无雾图像。

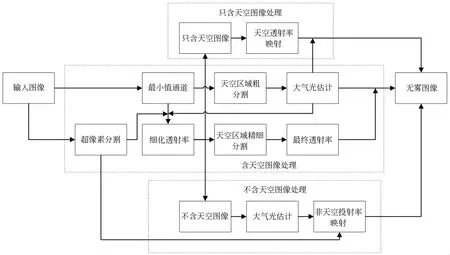
图1 算法原理框图Fig.1 Block diagram of algorithm principle

3.2 粗分割天空区域求大气光值

估计大气光值的区域应该尽可能地选择在天空区域，首先依据图像最小值通道图像，粗略的分割天空区域，为保证选取大气光值的区域处于天空区域，只保留最大连通区域作为分割结果。首先得到图像最小值通道，如图2（a）所示，其表达式为：

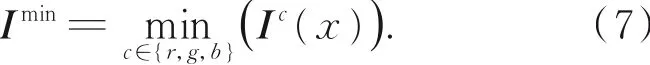
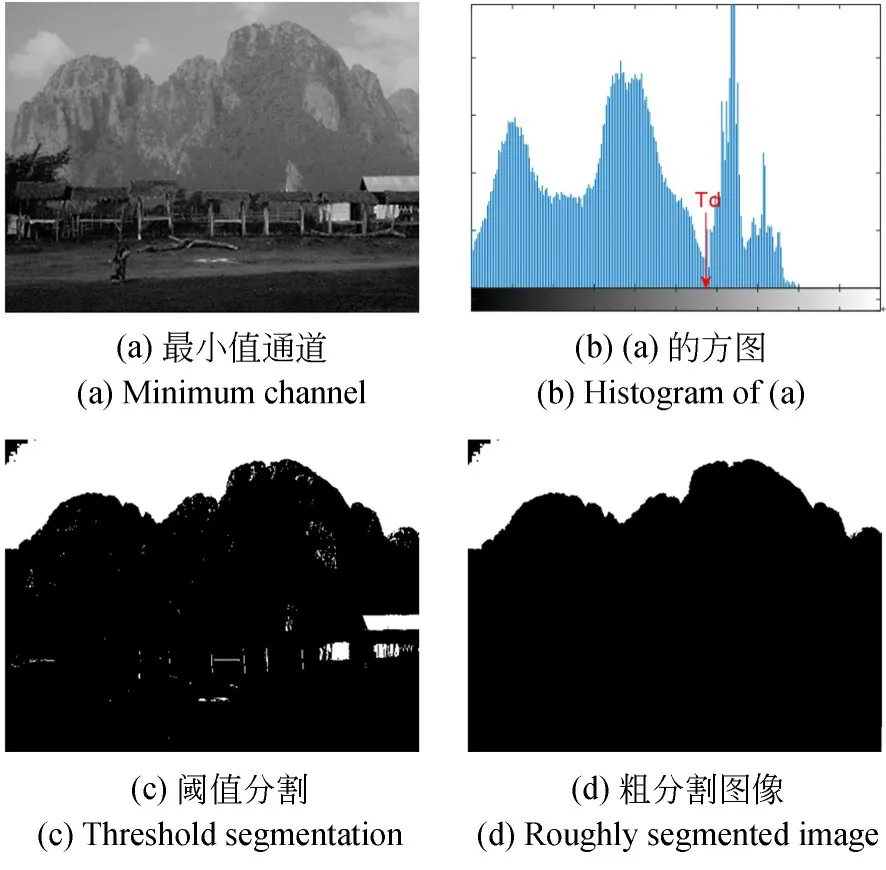
图2 天空区域粗分割Fig.2 Rough segmentation of the sky area

如图2所示为粗分割图像天空区域过程，阈值Td取在最小值通道图像直方图右侧第一个谷底处。为避免白云和白色物体影响，需要对阈值作约束，即阈值要满足右侧像素数大于总像素数的5%，否则将阈值取于下个谷底处，分割图像如图2（c）所示。此时分割的图像会包含图像非天空区域的白色物体，为了估计更准确的大气光值，只保留最大连通区域作为估计大气光值的区域，记为seg1，如图2（d）所示。这种分割将真实天空区域的大部分区域分割出来，虽然不适合作为3.4节透射率映射的区域分割，但对于估计大气光值这个目标是合适的。则大气光值可以表示为：

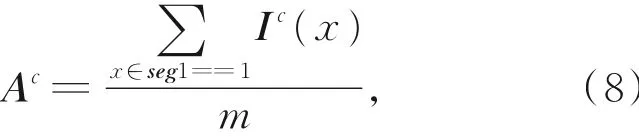
其中：c表示RGB三通道，m是seg1中值为1的像素数。

3.3 超像素分割改进暗通道求解透射率

传统暗通道先验算法计算暗通道时使用最小值滤波，在物体边缘区域计算暗通道时估计过小，如图4（b）中红色方框所示，这就是恢复图像产生halo效应的原因（彩图见期刊电子版）。

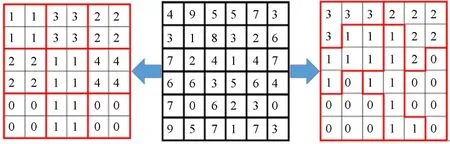
图3 最小值滤波和超像素分割求局部最小值原理图Fig.3 Schematic diagram of minimum filtering and super pixel segmentation for local minimum

图4 最小值滤波和超像素分割求局部最小值对比Fig.4 Comparison of minimum filtering and super pixel segmentation for local minimum

本文利用超像素分割［16］在局部小块区域分别求最小值代替最小值滤波操作，图3为二者的原理图。图4为两种方法分别对图2（a）最小值通道处理后的结果对比，得益于超像素分割的边缘保持特性，图4（c）中含有更多的边缘细节（如图中间的树枝以及房顶）。在图4中红框位置，图4（b）的山峰明显丢失了边缘而且高于原图像中的实际位置，而本文提出的超像素分割求局部最小值的处理结果基本与真实的边缘相似。

如图5（a）所示，超像素分割的小块数为1 000。相对于方形的窗口区域，超像素分割的小块区域内透射率是常数这个假设将更加适用，故使用超像素分割的小区域求局部最小值代替方形的最小值滤波，可以有效地减弱halo效应。

图5 透射率细化过程Fig.5 Process of refining transmission

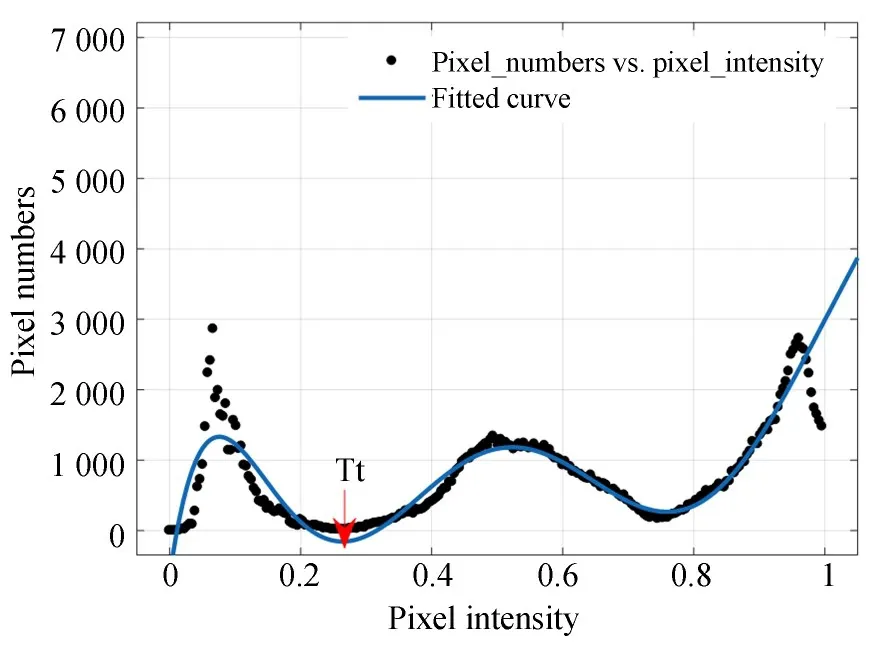
图6 拟合曲线图Fig.6 Fitted curve graph

首先结合3.2节估计的大气光向量值计算超像素改进暗通道，如图5（b）所示，其表达式为：

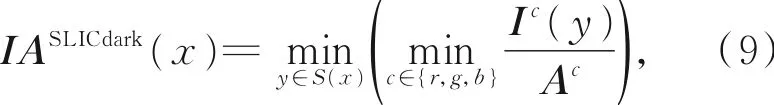
其中：SLICdark表示超像素暗通道，S(x)表示超像素分割的子块区域。本文由于提出的透射率映射方法有效地解决了天空区域和高亮区域存在的问题，故在估计透射率时不需要加入（5）中的调整因子ω，得到初始透射率如图5（c）所示，其表达式为：

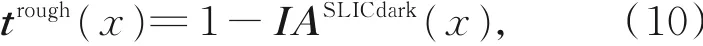
再对（10）得到的初始透射率进行导向滤波操作，得到细化透射率trefined(x)，此时若统计小于0.5的像素点数目大于95%，则判断图像只含天空，直接将trefined(x)利用天空透射率映射关系，获得最终透射率，再结合大气光值恢复无雾图像。否则如图5（d）所示，该图在天空区域和非天空区域有明显的边界，故对细化透射率使用自适应阈值法并保留最大连通区域可以将天空区域精细的分割出来，该分割图像记为seg，如图7（b）所示。

如图7（a）所示，阈值Tt自适应地取于细透射率直方图左侧第一个谷底处。具体操作是首先对直方图中的点进行八次多项式拟合，如图6所示。再以0.01的间隔对拟合曲线进行采样，最后经过逐点扫描确定第一个极小值点所在的位置即为阈值，阈值左侧对应于天空区域应该占整幅图像大小的5%，并且天空区域的透射率值应小于0.5，这可以作为判断图像是否含有天空区域的条件。

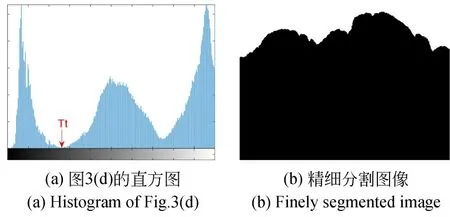
图7 天空区域精细分割Fig.7 Fine segmentation of sky area

若阈值满足上面两个条件，表示图像含有天空区域。当选取的阈值不满足以上条件时，默认该图像不含有天空，那么就需要重新估计大气光值，具体操作就是选取超像素分割暗通道最亮0.1%像素点处对应原图像中的像素值作为大气光值，然后利用超像素暗通道进一步估计透射率，将此透射率按照3.4节中非天空区域透射率映射处理后得到最终透射率，最后依据大气散射模型恢复无雾图像。

3.4 不同区域透射率映射及无雾图像恢复

在天空区域和高亮区域，像素的最小值通道往往趋近于A，观察式（4）可知，在这些区域内透射率趋向于0，暗通道先验理论在天空区域和高亮区域失效的原因就在于这些区域内透射率t(x)是一个很小的值，甚至部分区域内统一的当作定值0.1去处理。观察式（6）可知，当透射率在这些区域内被固定的设置为0.1时，恢复图像像素点间的差异就被放大了10倍，所以暗通道先验理论恢复的无雾图像在天空区域会出现明显的轮廓效应和颜色失真现象，如图11中He的算法［11］所示。

从理想的天空区域恢复效果可知，在天空区域，恢复图像在实现一定去雾效果的同时应尽可能逼近原图像，即：

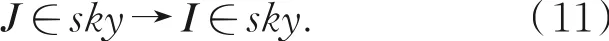
观察（1）可知要想满足上述情况，透射率t(x)将趋近于1。这和暗通道理论得到的天空区域透射率正好是互补的关系，假设映射后的透射率用t′(x)表示，则在天空区域有：

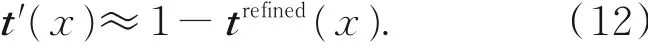
直接在天空区域应用（12）的映射关系会引起由于去雾程度不一致导致的视觉缺陷，所以需要在天空区域和非天空区域交界处透射率平缓地过渡来解决这一问题，由于交界处位于非天空区域一侧的透射率正好是精细分割所用的阈值Tt，故天空区域的透射率映射关系应该满足在靠近阈值处平缓的逼近边界处的阈值Tt。

高斯函数的衰减特性正好满足上述条件，其表达式为：

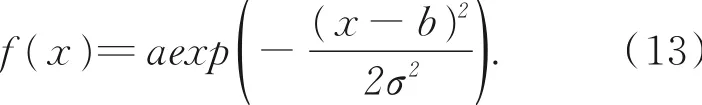
如图8所示，在自变量为3σ时，函数基本衰减为0，本文取自变量为0～4σ的高斯函数图像，并通过伸缩平移变换作为天空区域透射率映射关系，如图9中红色虚线所示。

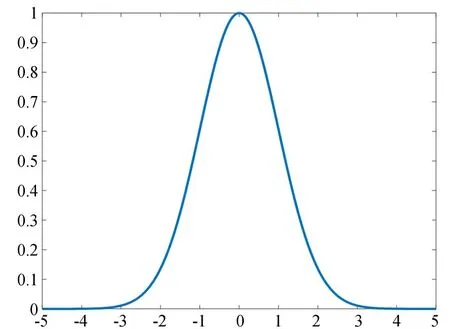
图8 高斯函数（a=1，b=0，σ=1）Fig.8 Gaussian function（a=1，b=0，σ=1）

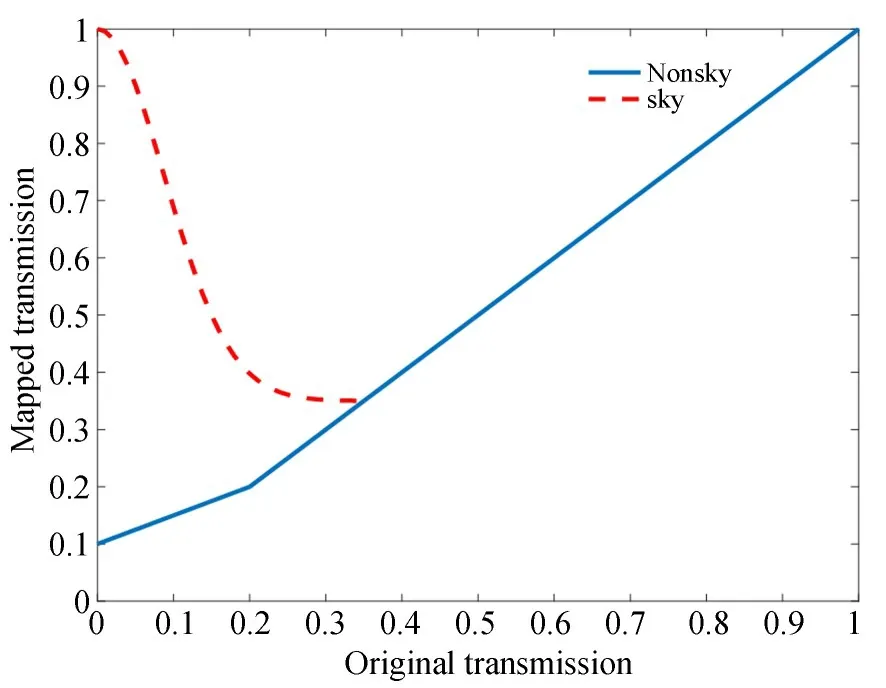
图9 透射率映射Fig.9 Transmission mapping

对于非天空区域，当存在大块白色物体的时候，He等［11］的算法同样由于透射率取为下限定值0.1，会产生颜色失真。本文将非天空区域透射率0～0.2线性的映射到0.1～0.2，由于透射率连续的变化，很大程度减弱了非天空区域在白色物体处产生的颜色失真现象，映射关系如图9中蓝色实线所示（彩图见期刊电子版）。最终映射透射率可以表示为：

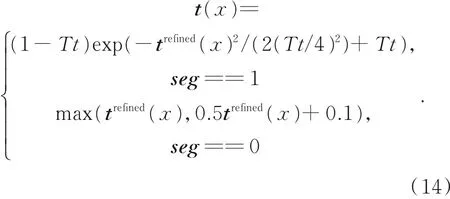
得到透射率和大气光值，便可以由（1）得到无雾图像：

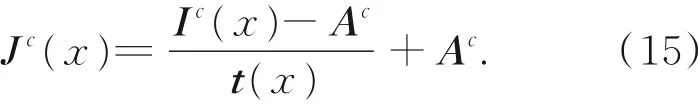
4 实验结果与分析

为了验证本文算法的性能，从主观评价和客观评价两个方面对本文算法和其他几种常用算法得到的结果进行比较。

4.1 主观评价

主观评价是由观察者对恢复图像进行观察，从主观感觉上对图像质量进行评价，主观评价可以最直观的反应去雾效果。本文所选的算法有He等［11］的暗通道先验算法、Meng等［17］的边界约束算法、Cai等［18］的基于端到端系统的算法、Ren等［19］的基于多尺度卷积神经网络算法、Berman等［20］的非局部去雾算法对比结果如图10～图12所示。

图10 为天空区域是蓝色天空场景下的有雾图像去雾效果对比，图10（b）在非天空区域表现良好，但是在天空区域过饱和，尤其在白云区域表现不自然；图10（c）在非天空区域出现颜色失真现象，在天空区域和非天空区域交界处存在偏色现象；图10（d）在天空区域表现出色，在非天空区域远景处去雾不彻底，在近景处颜色偏暗（如第二排图像树林处）；图10（e）在天空区域过饱和，在非天空区域出现颜色失真现象并且去雾不够彻底；图10（f）在天空区域表现良好，但是在非天空区域出现颜色失真现象，远景区域去雾不彻底；图10（g）为本文算法复原图像，在天空区域表现较为自然，没有出现过饱和现象，非天空区域去雾比较彻底且没有出现颜色失真现象，复原图像整体效果比较理想。

图10 蓝色天空图像复原效果对比Fig.10 Comparison of restoration effects of hazy images with blue sky

图11 灰色天空图像复原效果对比Fig.11 Comparison of restoration effects of hazy images with gray sky

图11 为天空区域是灰色天空场景下的有雾图像去雾效果对比。对于天空区域的恢复，He，Meng，Berman等人的算法均出现颜色失真现象以及轮廓效应，Cai，Ren和本文算法在灰色天空区域恢复较为自然。对于非天空区域的恢复，Cai和Ren的算法去雾不够彻底，Meng的算法在细节处颜色失真较为严重，Cai的算法近景区域偏暗，Berman的算法在细节处恢复过暗，丢失图像细节信息，并且存在颜色失真现象，He的算法和本文算法在非天空区域表现良好，本文算法比He的算法去雾更加彻底。综上所述，本文算法不仅在天空区域表现自然，且在非天空区域去雾彻底，在天空区域和非天空区域交界处也处理自然，没有出现因天空区域分割不够细致，将图像中天空区域当作非天空区域处理或者相反的处理，导致的在分割错误区域出现的异常现象。

图12 不含天空图像复原效果对比Fig.12 Comparison of restoration effects of hazy images without sky

图12 为不含天空图像的复原效果对比。Meng的算法在较远的区域出现偏色现象，Cai和Ren的算法在近景区域颜色偏暗，在远景区域留有残雾，Berman的算法在近景区域表现良好，但是在远景区域留有残雾，He的算法和本文算法对于不含天空图像去雾效果比较良好，颜色表现较为自然，相对于He的算法，本文算法去雾更加彻底。

4.2 客观评价

实验选取主观评价的6幅含天空有雾图像，分别采用He［11］，Zhu［13］，Wang［21］，Cai［18］，Ren［19］，Meng［17］，Berman［20］的算法与本文算法进行比较。采用无参考图像质量评估方法，将新增可见边率e，平均梯度r，饱和像素点比例σ以及处理时间t作为评价指标，越大的e和r及越小的σ和t表示图像的复原效果更好。最后求各项指标的平均值，实验对比数据如图13所示，各指标的表达式如式（16）～式（18）所示：

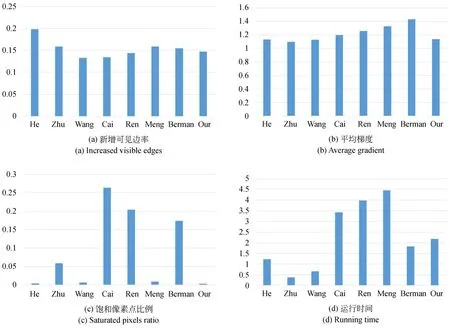
图13 客观评价Fig.13 Objective evaluation

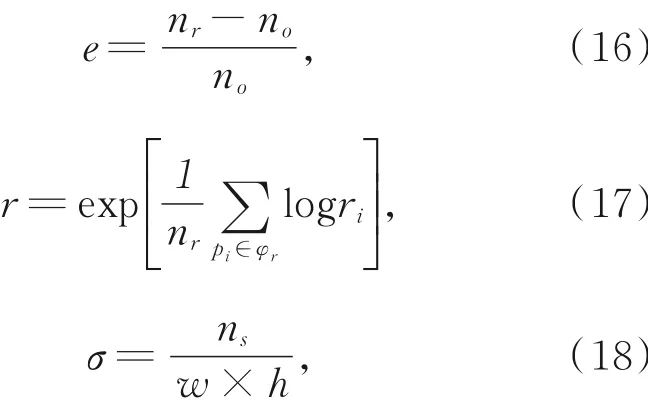
其中：no和nr分别表示有雾图像和去雾图像中可见边缘数量，ri表示去雾图像和有雾图像的梯度比，pi是可见边缘上的像素，φr是去雾图像的可见边集合，w和h是图像的长和宽，ns表示去雾图像中纯白和纯黑像素点的数量。

从对比的结果来看，本文算法在饱和像素点比例σ上取得了不错的表现，在归一化平均梯度r上取得了基本和其他算法持平的表现。对于新增可见边率e，因为选取的都是含天空图像，He，Zhu，Meng和Berman的算法在天空区域出现失真所以导致该指标表现较好，所以本文算法在该指标的表现上表现良好。对于运行时间t，本文算法相对于其他算法有较好的表现，但是不如He，Zhu和Wang的算法。综上所述，虽然运行时间上本文算法不及其他几个算法，但是在其他指标上均表现良好，考虑到本文算法在主观评价的良好表现，本文算法具有一定的优越性。

5 结 论

针对暗通道先验理论在天空区域复原图像时失效的问题，通过对问题产生的原因分析，提出了基于天空区域分割和透射率映射的方法有效地解决了这一问题。通过对天空区域的粗略分割，获得更为准确的大气光值。引入超像素分割的小块区域代替暗通道操作中方形窗口的最小值滤波操作，有效地减弱了块状效应和halo效应。实验结果表明，本文算法复原图像在非天空区域去雾彻底，在天空区域没有出现失真现象，天空恢复比较自然，整体复原图像表现良好。