在“变与不变”中感悟数学模型思想
【摘要】问题的解决离不开模型思想,而模型思想的感悟和形成也必须要经历抽象、归纳、推理等问题解决的过程。教师在教学中可以有意识地设计一题多解、一题多变或多题一解等问题解决环节,引导学生在“变与不变”中经历观察、猜想、类比、分析、归纳、表达、体验的学习过程,把握数学知识的本质,体会模型思想的结构化内涵和一般化思想,从而帮助学生感悟并初步形成模型思想。
【关键词】问题解决;模型思想;数学知识
模型思想是《义务教育数学课程标准(2011年版)》新增加的核心概念。数学模型就是根据特定的研究目的,采用形象化的数学语言,去抽象、概括地表述所研究对象的主要特征、关系所形成的一种数学结构[1]。利用数学方法解决实际问题时,首先需要建立数学模型。可见,问题的解决离不开模型思想,而模型思想的形成也必须要经历抽象、归纳、推理等问题解决的过程。所以对模型思想的感悟是在问题解决的过程中实现的。笔者就如何在问题解决的过程中培养学生的模型思想谈一些体会。
一、在一题多解中感知模型的数学本质
模型思想的建立是学生体会和理解数学与外部世界联系的基本途径,包括用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律。数学是抽象的,只有深入了解数学相关问题的本质特点,才能建立起真正的模型,而模型又能使我们对数学本质获得更全面、更深刻的认识和理解。
例如教师在执教六年级列方程解决问题时,提出“甲、乙两城市间的铁路经过技术改造后,列车在两城市间的运行速度从100 km/h提高到120 km/h,运行时间缩短了2 h。甲、乙两城市之间的路程是多少?”这一问题后,学生列出了两个截然不同的方程:(x/100)-(x/120)=2和100x=120(x-2)。笔者先不作解释,而是请学生思考这两个方程是否都可行。学生在比较、观察后发现,第1个方程是设甲、乙两城市间的路程为x,此方程的等量关系为:原来需要的时间-提速后需要的时间=2 h。而第2个方程对应的等量关系为:提速前甲、乙两城市间的路程=提速后甲、乙两城市间的路程,其中x表示的是提速前所需的时间。通过辨析,教师着重引导学生在对比、沟通中深刻感受两个方程虽然不同,但只要找到等量关系,根据等量关系列出方程就能解决问题。
整个解题过程教师鼓励学生先自主尝试,再组织学生观察、比较,引导学生逐步发现一题多解的共性,让学生充分感受数学问题中等量关系的重要性,深刻感悟方程构建的数学本质。这时学生学到的不仅仅是用方程解决问题,更重要的是懂得从具体的方程中抽象出数学本质,增强学生抽象概括的数学观念和数学意識,并积累建模经验。
二、在一题多变中建立模型的结构化内涵
数学模型是一种结构,要在小学数学课堂中引导学生感悟模型思想,需要教师有意识地呈现隐含某一模型思想的结构性素材,引导学生在问题解决中感悟素材中内隐的、本质的结构。
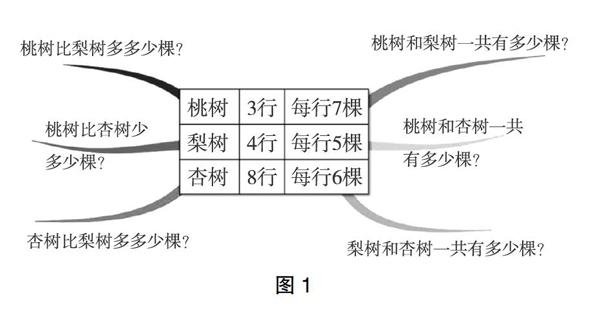
例如教师在执教苏教版数学四年级上册“解决问题的策略”第一课的例题后,请学生根据题中条件(如图1),试着提出其他的数学问题(三步计算的问题)。
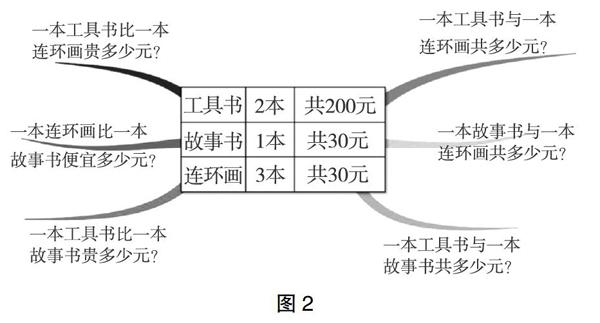
在学生发散思维,提出多个问题之后,教师用课件呈现学生所提出的问题并追问:①图1左侧的这些问题有什么相同之处?图1右侧呢?②图1左右两侧相对应的两个问题有哪些相同之处或存在什么联系?学生在比较思考中感受到不同的问题其实有着相同的内在联系,例如对于图1左侧的问题,在解决的过程中所涉及的数量关系(数学结构)都是“两积之差”,而右侧所有问题的数量关系均为“两积之和”。若是左右两侧联系对比,学生会发现不同问题所对应的树木类型相同,不同的只是运算类型。这个过程学生虽未动笔解题,但能体会到数学模型在解决问题中具有举一反三、触类旁通的效果。接下来,教师引导学生继续往下思考:如果是其他条件,还可能是什么条件?根据这些条件又可以提出哪些数学问题?学生在根据条件提出相应问题的基础上,小组合作自编条件并提出数学问题(如图2)。
学生思维迸发,创编新的条件,自然而然衍生出新的问题。如图2,整个数学模型变成了“两商之和”和“两商之差”的问题。因为有了前面的结构化经验,所以这个问题对于学生而言就不难解决了。通过上述学习,学生在类比、归纳中强化了模型的稳定性和结构性,巩固了基本数学问题的解决方法,提高了数学学习能力,培养了结构化思维,深刻感受到数学建模的价值。
三、在多题一解中凸显模型的一般化思想
《义务教育数学课程标准(2011年版)》指出,数学教学应该让学生亲身经历将实际问题抽象成数学模型并理解运用。从某种意义上来讲,模型思想要求我们将一个问题的解决拓展为一类问题的解决。
例如在苏教版数学六年级下册“工程问题”一课中,教师在引导学生解决问题:“修一段420米长的路,甲队单独修需要10天完成,乙队单独修需要15天完成。如果两队合修,几天能够完成?”后,将总路程改为“200米”“1800米”,学生惊讶地发现不管怎么改变总路程,工作时间都是6天。教师继续引导学生逐步抽象概括,在比较辨析中提炼出工程问题的基本数量关系,并适时删除路程条件,学生交流讨论后得出以下解法:1÷[(1/10)+(1/15)]=6(天)。教师相机指出:像这种问题在数学上叫作工程问题,它的特点是把工作总量看作单位“1”。在教学中,教师首先引导学生通过观察、比较和分析这些题目之间的联系,抽象出“工作总量可以看作单位‘1”这一规律,然后再运用这一规律解决更多相关的问题,这就是模型思想一般化的魅力。最后,教师继续引导学生将习得的方法尝试解决以下问题。
问题1一批货物,大车单独运,10次可以运完,小车单独运,15次可以运完。如果大车和小车合运,几次可以运完?
问题2甲、乙两地相距300千米,快车3小时可以行完全程,慢车6小时可以行完全程。快车和慢车同时从甲、乙两地相对开出,经过几小时可以相遇?
学生在解决问题的过程中发现运货问题、相遇问题与修路问题,都可以归结为同一类问题,且都可以按照工程问题的方法来解决。这一教学环节不仅加深了学生对工程问题的特点与规律的理解,还帮助学生更好地实现了对数学问题的抽象概括,即一般化。
实践证明,教师可以有意识地设计一题多解、一题多变或多题一解等问题解决环节,引导学生在“变与不变”中把握数学知识的本质,学会用数学的眼光观察生活,用数学的思维方式思考问题,经过结构化、一般化等学习过程,不断提高学生学习数学的兴趣和应用意识,同时帮助学生初步形成模型思想。
参考文献:
[1]徐利治.数学方法论选讲[M].武汉:华中工学院出版社,1983.
(责任编辑:陆顺演)
【作者简介】金妤茜,一级教师,苏州市教坛新苗,苏州工业园区学科带头人。

