基于逻辑推理素养下的高中数学立体几何教学策略探析
徐晓华
[摘 要] 逻辑推理是学生发现和解决问题的重要方式,是学生构建数学体系、有逻辑有条理地与其他学生进行交流和讨论过程中所必不可少的能力. 文章以苏教版高中数学“直线与平面垂直的判定”教学为例,探讨了逻辑推理素养视角下高中数学立体几何教学策略.
[关键词] 逻辑推理素养;高中数学;立体几何
作为六大数学核心素养之一的逻辑推理素养,意指从一些命题和事实出发,充分应用归纳、类比等规则推理出其他命题,它能有效发展学生的思维、开发学生的智力、培养学生严谨科学的精神,可以说是学生构建数学体系、有逻辑有条理地与其他学生进行交流和讨论过程中所必不可少的能力[1]. 而当前高中逻辑推理素养的培养并不理想,体现在学生逻辑推理方面主要为阅读题目粗心大意,解题逻辑思维混乱,总结反思、知识梳理常常流于形式,特别是在高中立体几何教学中,所含概念繁多、抽象并且概念与概念之间具有很强的逻辑性. 因此,以高中立体几何教学为载体,探究逻辑推理素养下的高中数学教学策略成了增强学生综合素质、培养学生创新思维、落实课程改革“立德树人”任务的关键.
逻辑推理素养下高中数学立体几何教学策略
1. 注重数学概念,牢固树立逻辑推理基石
基础知识是解决一切问题的根基,是进行逻辑推理的基石. 针对当前部分高中学生证明问题结论时,不能正确应用或没有意识应用所学定理和相关概念的现状,教师可以让学生一开始接触新概念时,就让学生从本质上理解它,深度掌握该概念的内涵、外延以及可能应用之处. 在具体实践中,教师可以从一些趣味问题或故事情境入手,然后通过呈现事物的方式有效加深学生的印象,有效避免学生死记硬背新概念的现象;并在此基础上,适当加强基础知识的变式练习,从而达到举一反三、深度掌握基础知识和基本方法的目的.
2. 聚焦问题情境,有效创造逻辑推理起点
推理源于问题,而问题情境的创设不仅可以引发学生产生认知冲突,而且还可以促使学生之间相互交流和沟通,有效创造出逻辑推理的起点[2]. 在具体教学实践中,教师应源于数学本身,或者从其他学科汲取,或者从学生息息相关的生活出发创设问题情境,设置教学任务,从而达到激发学生学习兴趣、引发学生思维碰撞的目的.
3. 鼓励合情推理,渗透逻辑推理规则
不难发现,在情境创设之后相当数量的学生会出现无从下手的情况,因此教师应一改传统以讲授为主的教学方式,鼓励学生大胆地通过类比、归纳的方式进行猜想,让学生敢于将自己的真实想法表达出来,并根据题目已知条件主动地进行探究性活动,促使学生在活动探究中获得最为深刻的知识. 值得说明的是,在此过程中教师应及时融入类比和归纳等推理方式,并给予学生足够的时间和自主探索、合作学习的空间,有效地促使学生亲身经历合情推理的过程.
4. 演绎推理验证,示范逻辑推理过程
合情推理与演绎推理是相互联系的,只有经过严格数学证明之后的命题才能称为定理. 因此,在学生自主探究猜想得出相关数学命题之后,教师还应依靠演绎推理的严格论证获得定理,并在此过程中不断强化数学逻辑语言的表达[3]. 在具体实践中,为了充分暴露学生的思维推理过程和规范书写等问题,促使学生加深对所学知识的印象,教师可以先让学生尝试自己的证明,然后呈现严格的证明过程,从而帮助学生厘清论证思路,改正自己不良的学习习惯,有效提升学生的逻辑推理能力.
5. 构建知识体系,梳理逻辑关系
归纳总结也是逻辑推理素养下高中数学立体几何教学中不可或缺的环节,因此为了帮助学生厘清知识脉络,教师还应鼓励学生通过构造知识结构图的方式将相关概念、命题以及定理之间的逻辑关系有条理地呈现出来,有效提升学生分析、发现的逻辑推理能力. 值得一提的是,针对学生不会运用概念图的形式进行概括总结的现状,教师应在课堂教学中适当进行示范.
逻辑推理素养下的高中数学立体几何教学实践
仅有相关理论是不够的,并且理论与实践是相互结合的. 因此,基于以上逻辑推理素养下高中数学立体几何教学问题情境创设、知识体系构建等策略,下文以苏教版高中数学“直线与平面垂直的判定”教学过程为例进行深入探究.
1. 创设情境,引出定义
为了激发学生探究的兴趣,培养学生的爱国主义情怀,促使学生直观感知直线与平面垂直的本质,教师应结合教学内容,及时利用多媒体播放并介绍日晷这种我国古代普遍使用的计时仪器以及计时原理,然后要求学生逐一思考以下几个问题:
问题1:古代在制作日晷时,如何能够准确判断晷针与晷盘垂直.
問题2:为了有效解决上述问题,如何将日晷计时过程数学化.
问题3:试着应用自己的语言,归纳总结出直线与平面垂直的定义.
2. 设置问题,得到猜想
为了促使学生掌握逻辑推理规则,有效引发学生的认知冲突,教师应根据线面垂直的定义,推理出若要使得晷针与晷盘垂直,则需要判断出晷针与其在晷盘内形成的每一个影子垂直,显然这是非常困难的,也是不太现实的. 于是,为了降低学生思考的难度,教师应采用类比方式,就地取材,要求学生观察类似教室内暖气供水管与屋顶面、书立侧棱与书立底面之间的特征(如图1、图2所示). 由此引导学生猜想出若想获得一条直线与平面垂直,则需要这条直线与该平面内的两条相交直线垂直即可.
3. 操作确认,规范证明
为了有效验证学生的猜想,帮助学生在课堂上获取基本活动经验,有效强调猜想中“两条”“相交”等关键词语,教师应引导学生通过如图3、图4的方式完成教材中所设计的探究活动,并思考教材所提出的问题.
然后要求学生应用图形语言和符号语言表示直线与平面垂直的判定定理,并要求学生结合日常实际列举生活中直线与平面垂直的实例. 在此基础上,为了进一步帮助学生厘清概念和定理之间的逻辑关系,有效规范相关的证明过程,教师还应及时呈现如下题目,要求学生先行分析思路并进行证明,然后由教师板书示范过程.
4. 变式练习,归纳反思
为了进一步加深学生对直线与平面垂直判定定理的理解,促使学生在反思归纳时有目标、有方向,教师还应及时结合教材例题和相关的练习题目,要求学生独立完成如下的变式题目:
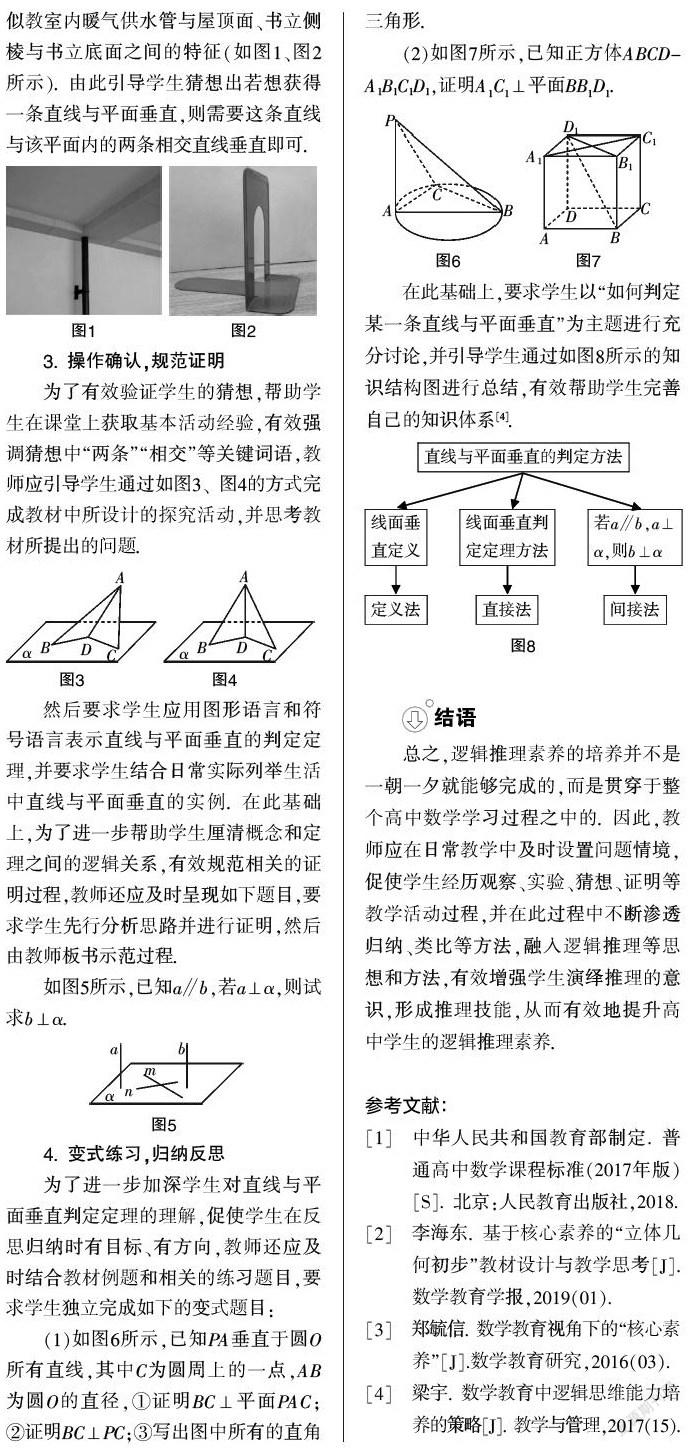
(1)如图6所示,已知PA垂直于圆O所有直线,其中C为圆周上的一点,AB为圆O的直径,①证明BC⊥平面PAC;②证明BC⊥PC;③写出图中所有的直角三角形.
(2)如图7所示,已知正方体ABCD-A1B1C1D1,证明AC⊥平面BBD.
在此基础上,要求学生以“如何判定某一条直线与平面垂直”为主题进行充分讨论,并引导学生通过如图8所示的知识结构图进行总结,有效帮助学生完善自己的知识体系[4].
结语
总之,逻辑推理素养的培养并不是一朝一夕就能够完成的,而是贯穿于整个高中数学学习过程之中的. 因此,教师应在日常教学中及时设置问题情境,促使学生经历观察、实验、猜想、证明等教学活动过程,并在此过程中不断渗透归纳、类比等方法,融入逻辑推理等思想和方法,有效增强学生演绎推理的意识,形成推理技能,从而有效地提升高中学生的逻辑推理素养.
参考文献:
[1] 中华人民共和国教育部制定. 普通高中数学课程标准(2017年版)[S]. 北京:人民教育出版社,2018.
[2] 李海东. 基于核心素养的“立体几何初步”教材设计与教学思考[J]. 数学教育学报,2019(01).
[3] 郑毓信. 数学教育视角下的“核心素养”[J].数学教育研究,2016(03).
[4] 梁宇. 数学教育中逻辑思维能力培养的策略[J]. 教学与管理,2017(15).

