高中数学教学效率的案例研究

[摘 要] 文章通过对2019年高一新生在人教A版必修1函数模块的入门教学的案例研究,发现学生个体和班级整体对数学题型学习与发展的规律及教学效率的影响因素,并根据案例分析和教学经验提出了高效的高中数学教学的基本原则和策略.
[关键词] 高中;数学教学;效率
研究背景
从20世纪80年代以来,我们进行了一系列的数学教学改革,但大多数都销声匿迹了,其中最致命的原因是缺乏效率意识. 这告诉我们,改革者有无效率意识,改革方案能否实施高效的数学教学,乃是一项硬指标,是具有否决权的“一票”[1]. 国内有关数学教学的效率和有效性的研究文献很多,说明对这个问题的关注度高,但纵观国内外关于数学教学效率的研究,尚存在以下问题或不足:(1)脱离具体的教学内容和教学目标而空谈效率;(2)缺乏课堂教学后学生实际学习效果的跟踪调查研究,教学效果如何是由学生的学习成果来决定的. 文章就是对自然教学情境中高中数学教与学案例进行的跟踪调查研究.
研究方法
1. 采取行动研究法,质性和量化分析结合
由于教育的高度复杂性,严格控制的对比实验研究在学校难以进行,所以在自然、真实的教育环境中进行“行动研究”就成了可行和必要的方法. 笼统的教育量化分析可以看到外部的整体特征,但难以洞察到复杂的教学现象的内在本质,所以教育研究要将质性和量化结合. 案例分析对发现教育的问题和本质是不可或缺的,有道是“一个好的案例,胜过一千次说教”.
2. 研究对象和过程
研究对象主要是2019年9月新入学的笔者任教的高一(13)班的学生. 这所福建省一级重点高中每年高考的一本上线率在35%左右,本科上线率在90%左右. 这个普通平行班(共50人)预计能达到一本上线十几人的水平. 重点是调查研究高一上学期期中考试前2个月的教与学的情况,此时正是高一新生的数学入门学习阶段,学习的内容又是比较抽象、难学的人教A版必修一的函数,学生的学习困难很多,易于发现问题. 笔者对(13)班学生使用了自己设计的数学作业和相应的教学方法,用作对比的是采取传统的教学方式和教辅作业的另一笔者任教的(11)班和其他平行班,年段有2~14共13个平行班.
研究结果与分析
1. 案例1:复合函数的单调性问题
(1)课后作业训练的变式进程——分析复合函数的单调性:第一次,f(x)=;第二次,f(x)=;第三次,y=;第四次,y=;第五次,y=;第六次,f(x)=log(1-x2);第七次,f(x)=lg(3-2x-x2).
(2)高一(13)班整体教与学的进程及分析:
第一次(9月12日),课堂上教师讲析一个范例后,学生做了一个匹配练习题(没有板演);教师再讲析,此题作为课后作业的正确率是34%.
教学反思:教师认为这种题型的解法步骤简单明确,讲解也很清晰,出现这么差的教学效果真是出乎意料. 经过深入的访谈等调查分析,发现主要原因是高一新生难以理解这种初中没有学过的形式化的抽象代数推理. 不理解的内容易忘记,也无法自己推求,晚自习做匹配练习时就记忆模糊、混乱,无所适从了.
第二次(9月17日),课堂上对前函数的单调性和奇偶性进行阶段性复习,并匹配相应的课后作业,此题属于作业中的“错题再练”,结果是54%的正确率,进步显著.
第三次(9月21日),此题作为最后的“预习探究”作业,结果只有12%的正确率. 可见高一新生应对较新的变式问题时处理能力很差,在此入门阶段的学习,多数学生还是处于模仿的学习状态.
第四次(9月23日),在上课的最后讲析了此类范例,但因时间不足,没有当堂匹配练习,结果是此题作为课后作业只有26%的正确率,教学效果很差.
第五次(9月24日),此题作为课堂上讲评后的课后作业之“错题再练”,结果是82%的正确率,进步显著.
第六次(9月28日),课堂上讲析了范例,此题作为课后作业是70%的正确率,说明(13)班大多数学生对此类题型的掌握渐入佳境.
第七次(10月30日),作为当天下午第二节的课堂测试,此题的结果居然是只有34%的正确率. 进一步对学生的访谈发现,不会做或做错的主要原因是淡忘了教師教的此类题型的解法. 经过教师的提示,学生回想起来之后,多数学生又能解答出来了.
(3)代表性的学生个案学习进程与分析.
①数学成绩是班级的后10名,悟性较差,但学习认真的女生吴:第一次的作业正确,第二次的作业错误,第三次、第四次、第五次的作业都正确,第六次、第七次的作业又错误了. 调查和访谈发现,此女生因学习认真,课堂笔记做得较清楚,即使不怎么理解,也可以通过逐步模仿正确解答,但间隔时间一长就容易因为淡忘而不会做或做错.
②数学成绩在班级10名至20名之间,悟性较好,但作业马虎的男生林:第一次、第二次、第三次、第四次、第五次、第六次的作业都错了,第七次测试过程虽不规范,但结论正确. 错因主要是其不按照教师示例的三步去推求,订正也不认真,总是习惯于随心乱写,思维不严谨.
③数学成绩在班级前10名的优秀男生黄:除了在第四次的作业因“跳步”、太匆忙而发生了错误外,其他几次作业全部正确. 这样多次的重复训练对此水平的优秀学生有些不必要了.
教学反思:对比女生吴和男生林的学习过程发现,严格落实学生规范解答的要求对促进学生掌握数学和提高教学效率具有必要性. 因为数学是研究模式的科学,大多数常规题型的基本解题过程都可以“算法化”分步操作,这样易于学生先学会模仿操作和减少错误,然后在操作中逐步理解,而且规范化操作有利于促进学生快速准确地解答基本题型.
案例分析后发现,虽然学生的最后答案是在正确与错误之间摆动,但在总体上其理解和掌握是对错误的反思纠正而前进的.
2. 案例2:分段的奇函数问题
(1)课后作业训练的变式进程:第一次,作业为“设f(x)是定义在R上的奇函数,已知当x≤0时,f(x)=2x2-x,求f(x)的解析式”;后继的变式作业只是对“已知”做了诸如“当x>0时,f(x)=lgx+x-1”等方式的改变,其他不变(详略).
(2)高一(13)班整体教与学的进程及分析:
第一次(9月14日),课堂上讲析了此类范例,但没有时间做匹配练习,课后此题作为作业只有34%的正确率.
第二次(9月16日),在前14日“讲练评”一轮后,课后此题作为作业仍然只有38%的正确率.
教学反思:就一步如“当x>0时,-x<0,则f(x)=-f(-x)…”的推理就可以解答的问题,学生居然会学得如此困难,出乎教师的预料. 对学生解答的分析和访谈发现,根源是学生难以理解这种形式化推理的必要性和合理性. 教师自觉此题的解法简单明了,认为只要示范讲明,学生模仿着做就可以掌握了. 岂料学生总是倾向于用自己的理解(即学习过程中形成的思维表象)来解题,因为学生头脑中的“表象”是思考时最先跳出来的、最活跃的心理因素[2]. 案例一和案例二都表明了对数学的理解是学生自主建构的,把学生当作知识的容器,一味地讲授灌输式的数学教学效果是很差的.课堂上要注意通过学生独立尝试练习后的师生互动,通过正例与反例的对比分析及独立练习等用来丰富和完善学生的“基本活动经验”和认知表象,这样才能真正提高学生的理解水平和解题应变能力,这样才是真正高效率的数学教学.
第三次(9月17日),在前“错误”课堂讲评后,此题作为“错题再练”,结果是68%的正确率,进步显著.
第四次(9月19日),课堂的单元考试,此题是72%的正确率.
第五次(9月23日),此题是79%的正确率.
第六次(10月30日),当天下午第二节的课堂测试,此题居然只有26%的正确率. 绝大多数学生因为淡忘、没有思路或思路不清而错.
(3)代表性的学生个案学习进程与分析:
①同上,后进生吴:第一次、第二次属于思路不清的错误,第三次正确,第四次考试错误,第五次正确,第六次属于思路不清的错误.
②同上,中等生林:第一次、第二次、第三次、第四次都是属于思路不清、逻辑混乱的错误,虽有订正,但总是不按照教师示例的步骤推理,习惯于自己乱写而错. 第五次正确,第六次测试没有思路,显示空白.
③同上,优秀生黄:每次都正确.
3. 案例3:分段函数的单调性问题
(1)课后作业训练的变式进程:第一次,作业为“已知f(x)=x2-2x-3a,x≥2,(a+2)x-1,x<2 是(-∞,+∞)上的单调递增函数,求实数a的取值范围”;后继的变式作业只是对区间划分和函数稍作了改变,比如加入了后面学习的指数函数或对数函数,形式和难度基本不变(详略).
(2)高一(13)班整体教与学的进程及分析:
第一次(9月12日),当天只在课堂上讲析了一个范例,没有匹配练习,结果是此题作为课后作业只有34%的正确率. 课堂范例分析能使学生对解决此类题目有一个大致的思路,但从作业效果来看,对这类较复杂的问题,没有当堂的独立练习和讲评,大多数学生难以掌握思路.
第二次(9月17日),这是阶段复习后的“错题再练”作业,此题的结果还是34%的正确率.
第三次(9月19日),在课堂的单元考试中,此题作为填空题的第12题,只有38%的正确率.
第四次(9月21日),试卷讲评后的“错题再练”,此题是40%的正确率.
第五次(9月24日),又是“错题再练”,此题是70%的正确率,终于取得了显著的进步.
第六次(10月30日),课堂测试,此题居然只有18%的正确率,可怕的遗忘!
教学反思:通过作业分析和访谈发现,虽然课堂上学生听懂了大致思路,但具体操作仍是生疏易错,有些学生对含参数的函数画示意图感到困惑. 教师反思后再次讲析此类题型时,把解法进行了“算法化”的分步操作处理,并且是讲析一步让学生做好一步的笔记,这样易于学生模仿. 经过反复变式训练后,终于取得了显著的进步;但进步还是太慢,效率低下,如果早点改进教法,并集中、强化变式训练,效率会更高.
(3)代表性的学生个案学习进程与分析(详略).
4. 案例4:班级整体的对比分析
第一次是在10月8日的高一年段月考中(考试内容是第一章到第二章的对数的运算,满分120),(13)班的數学平均分是69.2分,比(11)班高6.6分,比其余12个平行班的总平均分高6.5分. 第二次是在11月16日的高一年段期中数学考试中(考试内容出自必修一,满分150),(13)班的数学平均分是117.4分,比(11)班高6.4分,比其余12个平行班的总平均分高8.4分. 可见(13)班的数学平均分显著高于其他对比班,进一步的各试题所得平均分的对比分析都表明了短期内造成如此显著差距的一个主要原因就是(13)班的数学教学采取了教师自己设计的预设与生成结合的作业,实现了对核心重点的内容或题型的循环巩固,以及变式递进的训练.
研究结论与建议
1. 研究结论
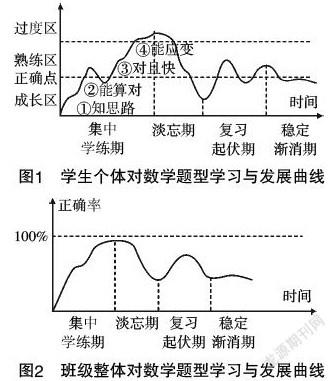
对基本题型的掌握是学生数学理解和能力发展的基础,是数学教学的重要内容.结合上述案例分析和教学经验,从一般性来看,学生个体或班级整体对数学相对较难题型的学习发展具有以下曲线显示的阶段和特征:
从数学题型学习与发展曲线可知,要提高教学效率,一是开始的学习要趁热打铁,集中连续地学练到位(以“讲练纠”或“练纠”的方式变式递进),并达到一定的熟练度,为后继的变式提升奠定基础;二是要科学设计练习让知识循环巩固,提升“长作业”练习体系. 而下列的数学教学方式是低效的:(1)课堂上一味地讲授,缺乏师生互动和学生独立的尝试练习;(2)传统的知识本位的线性前进的教与练,缺乏对前面所学知识的循环巩固,这样会导致学生学了后忘了前的“漏勺”式的低效教学现象的出现;(3)没有系统的“长作业”式的巩固提升变式训练,这样会导致学生的学练不到位,加之遗忘而功败垂成;(4)训练到位后的再重复训练可能就是过度低效了;(5)学生缺乏新知识学习所必要的基础,这是高一数学入门教学困难的首要原因.
2. 教学建议
结合研究结果和长期的教学经验,笔者提出以下高效的高中数学教学的基本原则和策略:
(1)“以学为本,教服务于学”是保证教学效率的基本理念和前提. 教师头脑中存在的潜意识的知识本位和教师本位的观念使得教师认为教学就像“扔包袱”一样把知识讲清楚教给学生就行了,不关心学生实际的接受情况,结果是教学低效到不如自知. 所以保证教学效率首先是要树立“以学为本,教服务于学”的理念,教师始终要有意识地“稚化”自己的思维,想学生之想,预学生之困,并跟踪调查学情,这是发现学习问题和获得适合学生的高效教学的前提.
(2)一条主线——螺旋上升,分层前进式的学生学练活动. 数学教学的落脚点不是教师“教完”,而是学生“练会”. 从前面“对数学题型学习与发展曲线”可知,适合学生数学认知发展规律的循环巩固,螺旋上升式的数学学练活动对保持和提高数学教学效率是不可或缺的. 从案例研究中也会发现分层教学,尽量使每个学生获得与之相适应的教与练,对提高教学效率,特别是防止和转化学差生是不可或缺的.
(3)一个依托——教练一体系统优化的课后作业[3]. 传统的线性前进的数学作业,无法满足螺旋上升、分层递进的数学教学要求,所以设计出一套高质量的教练一体系统优化的课后作业是高效数学教學的依托,也是破除低效的“题海战术”的关键. 循环往复变式递进的训练是必需的,但要把握好“度”,这就是要根据作业中学生反馈的信息来看学练是否到位,还存在哪些问题,并据此及时调整后继的教与练,所以课后数学作业要将预设和生成结合才能最好地适合学生,避免盲目低效的“题海”训练,从而获得高效的教学成果.
(4)一个保障——激励与督促结合的教学管理. 从案例分析中可知,教师的严格管理,努力使每个环节的教学要求落实到位,是学生个体和班级整体有效学习进步的保障.
参考文献:
[1] 于新华,王新兵,杨之. 对“数学教学效率”研究的几点思考[J]. 数学教育学报,2006(15).
[2] 李士锜. PME:数学教育心理[M]. 上海:华东师范大学出版社,2001.
[3] 钟志敏. 教练一体系统优化的三角函数教学[J]. 数学通报,2016,55(06).

