在结构化中深度理解算理

钱建兵

摘 要 计算教学需要理解算理，而算理的理解需要以直觀去构建运算的意义，将计算的意义与数的意义统一起来，形成结构化的理解。在抽象算法的过程中，需要回到直观，寻找意义，提升直观，形成形式化、符号化的表达与理解，最终概括为算法，达到算理直观与算法抽象的统一。

关键词 结构化 算法 算理

计算教学需要理解算理。对算理的理解，从学生已有知识结构的角度讲，在于学生对数的表征与理解，以及对运算意义的理解，在于发挥数学知识整体的功能去促进算理的理解，注重算理生成的全过程与算法抽象的全过程。动手操作、直观模型等是理解算理的重要方式，但更要注重对直观进行有层次的抽象，最终促进算法的形成。

一、理解意义：知识结构中寻求深刻

对计算意义的理解是理解算理与习得算法的前提与基础。小数、分数四则运算与整数四则运算意义是一致的，理解运算意义的基本原理，生成计算的知识结构，需要基于学生对数的知识与经验。运算是对数的运作，对运算意义的表征离不开对数的表征。而学生对数的表征是丰富的、有层次性的。以直观图形呈现学生对数的理解，如整数乘法中的格点图，分数运算中的线段图、矩形图，在此基础上可以直观地让数的意义、数的组成等算理理解的重要因素呈现出来，从而有利于理解运算的意义，形成整体的数的意义、数的运算的知识结构。

如分数运算的教学。分数的表征是丰富多样与多层次的。在分数加减法的教学中，学生会以线段图或饼形、矩形等来呈现运算的意义，这些方式源于他们对分数意义的理解。在教学分数乘整数时，可以用情境让学生表示出 米，激活对分数的相关理解，3个米就是米，用算式表示是 ×3。这样，对运算意义的理解就与对数的理解的经验相结合，学生初步了解分数单位乘整数，就是算含有分数单位的个数。然后在此基础上表示 ×3，结果里面一共有几个分数单位？通过直观图，有学生用加法算，也有学生用乘法3×3算，从而理解分数乘整数与之前学习的乘法意义一样，是单位的累加，在数的意义的基础上理解运算的意义。

学生的知识背景不同，对运算的内部表征是不一样的，然而并不是所有的直观表征形式都有利于学生发现算理。在教学中，重点把握利于意义生根的、反映本质化的因素——计数单位，实现运算意义与数的认识两个知识结构的联结，从而形成一个大的结构。同时，随着学习的深入，运算意义的内部结构也在不断更新。如分数乘分数，就是对整数乘法、整数乘法意义的拓展。真分数乘真分数，为什么积小了？通过直观图进行比较：分数与分数相乘，实际上是把原来的分数单位又平均分了一次，所以分数单位变小了，其本质与分数意义有相同的过程，分母相乘是先“平均分”;分子相乘，是再“数”，也是单位的累加。后续运算意义的理解，通过反思贯通，又反哺促进了对前期经验中运算意义的深刻理解。在教学中，理解意义，以图的直观呈现运算的意义，既需要与学生原有的认知结构对接，建构更大的知识结构，同时也要与学生的认知经验沟通联系，积极强化认知结构。

二、理解过程：经验结构中追寻意义

算法是一个程式化的操作过程，教学中，如果将这个操作过程的结果直接呈现给学生，学生将难以获取动态的操作过程，这样，即使有直观图，学生也无法将意义与算法直接关联起来。因此，在教学中，需要做好过程性理解，丰富学生的经验。教材呈现的都是算式的结果，对学生而言，看出结果是比较容易的，而静态图与动态计算过程如何联系起来，对学生而言，是有困难的。因为图并不是根据他们对算式意义的理解创造的，由于学生的经验结构不连续、不完善，如何看图，画图表征，如何看出画图背后的意义（思考过程）对学生是一个困难。因此，在教学中，需要做好“分解动作”，让学生经历算式表征的形成过程，理解每个“动作”表示的意义。

如分数乘分数的教学，由于其意义是求一个数的几分之几是多少，跟学生熟悉的整数、小数乘法的意义不一样，不是求几个相同加数和的简便运算，同时学生经验中并没有表示一个分数的几分之几是多少的经验。所以在教学中，需要在理解意义的基础上，逐步丰富学生的经验结构，引导学生经历算式图形表达的过程。先出示情境：一台收割机每小时收小麦  公顷，这台收割机  小时收割多少公顷？学生根据分数意义的理解，把1公顷平均分成两份，  公顷表示其中的1份，然后把  公顷平均分成了两份，就是  小时收割的。在学生表示出  小时收割多少公顷的基础上，根据图的直观总结理解分母相乘的算理，分数乘分数就是两次平均分，是对分数单位的再次均分，“单位1”平均分成的份数是两个分母的乘积，同时积累了用图形表征分数乘分数的经验。然后表示出 × 、  × 两个算式的意义，虽然学生理解意义，但是如何操作表示却存在困难，因为前面两个算式的表示，都是对一个分数单位再次平均分，而这里是把两个分数单位看作一个整体平均分，第二次平均分学生会出现困难，思维上的惯性使学生两次均分都是从同一个方向平均分的，如用图1表示×，这是学生结构中的断点。

可以引导学生思考：第二次平均分，需要能看出“单位1”平均分成了多少份。结合前面两次平均分的经验，可以知道一共是平均分成了15份，思考如何看出是15份，从而想到需要从另一个维度去分，如图2。这样，对分母相乘表示的意义又加深了理解，然后去思考，结果表示多少份，如何计算，分子相乘的意义就出来了。

直观操作的过程，为算理的直观表征与解释提供了经验。当然，教学中既要充分了解学生的内部表征，又要丰富学生进行表征的经验，提供各种表征工具，以各种教学手段，充分激发，使其外显，为教学提供充分的依据。

三、理解算法：思维结构中逐步内化

计算法则的推导，通常借助于具体的问题情境，以图形的直观，建立算理。在这个过程中，由算理直观到抽象为算法，是跳跃性的。如果抽象过程中的跨度高于学生思维的最近发展区，算法的理解就成为一种机械的过程，失去其意义。所以，在这里需要有效连接，要防止算理与算法的脱节，打通算理与算法的联系，引导学生的思维层级抽象。表征既是沟通工具，又是思维的材料。

1.在反思中寻找意義

算法的抽象需要算理的直观表征，当学生初步了解形成算法的直观表征后，为了强化对算法的理解，在抽象算法时能有效运用直观表征这一心理工具，还应该经历一个重新寻找意义的过程，以获得对算理的稳固的认识，为作为过程的算理凝聚为作为对象的算法进行过渡。

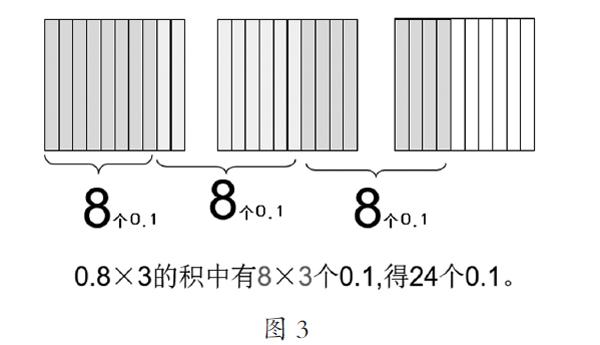
以小数乘整数为例。对数位如何对齐，可以从规定的角度进行说明，但数学规定是可以有意义的。在学生在正方形图中表示出0.8乘3后，追问，怎么让人一下子就看出表示的是3个0.8？学生加大括号将图进行改进（图3）。然后引导学生将意义与竖式过程进行联系：这个过程表示了竖式中的哪一步？看着图，你能不能说说先算8乘3表示什么意思？

通过过程之间建立联系、寻找意义，促进儿童头脑中图形表征的稳定性与进一步的概括性，此时的直观表征，已不完全是直观化、具体化了，而应促进其成为学生的一种抽象的心理工具。

2.在表达中内化算理

布鲁纳认为，儿童获得一个数学概念的过程是以线性方式从动作表征过渡到图像表征，最后到抽象思考。在算法的形成过程中，当具体的图像表征消失后，在儿童的头脑中能依据图形的影像，自己制作心像而进行内在的思维活动。在形成了直观的表征之后，要引导学生形成形式化的、符号化的表征。让学生在语言表述、符号表达等活动中将思维内化，将操作过程进一步凝聚、抽象，最终提炼为算法。

在整数乘小数的教学中，当建立起过程之间的联系后，进一步引导学生将表征抽象化、形式化，脱离具体操作与图形，想一想：0.15×3的结果中有（ ）×（ ）个0.01？计算结果的小数点点哪儿？为什么？小数点点哪儿跟什么有关？原来，小数点点哪儿是看它的计数单位。通过操作活动中的经验，学生理解小数点的位置跟一个因数的小数位置有关，其本质在于这个因数的计数单位。再如分数乘整数中，在结合操作理解算理之后，结合图形，让学生对算理的理解上升为一般化、概括化，可进行如下教学：×n（a≠0），可以怎么计算？说一说为什么这样计算？结合图形表征的理解，有了形式化的理解：学生用“表示b个乘n，结果有（ ）个”的语言，内化了算理，为抽象思考的算法概括阶段打下了基础。

总之，算理的理解需要建立在学生的知识结构中，从数的意义、运算的意义的结构中寻根，充分展示算理直观的过程，完善学生的经验结构，把握好算法与算理之间的联结，形成完善的运算结构系统，这个过程是一个整体，是通过过程直观、意义直观走向算法抽象的过程，因而也是学生思维发展的过程。

[责任编辑：陈国庆]