专题型微课在初中数学几何推理能力培养中的应用

南宁市第三十七中学 李明哲

微课是运用信息技术呈现数学片段教学的一类教学资源，具有主题突出、问题聚焦、时间简短、制作简便等优点，更有利于初中生数学核心素养的培养。课堂教学更多的是基于对全班学生整体水平的预估而进行的，进度基本统一，很难关注到所有学生的个性化需求。而且每个学生的认知基础、理解能力、接受能力、课堂专注度和学习习惯各不相同，同样的学习内容，不同层次的学生在课堂上的掌握情况各不相同。因此，课后可以针对不同学生的认知现状，设计专题型微课，实施更具针对性的教学。专题型微课既要考虑内容上的补充性，又要考虑学习对象的针对性。我校开发了一系列专题型微课，包括资源弥补型、拓展提升型、重难点解析型等系列微课，以“问题解决”为核心，注重数学思想方法的渗透，培养学生数学核心素养。同时，以年级为单位，组建基础群和提高群两种层次的学习群，不同层次的学生根据自己的学习情况选择学习群，教师在不同学习群推送难度不同的微课，同时辅以微课变式练习，让学生根据自己的情况选择微课学习和完成同步练习，自主完善知识体系，形成数学思维，提高数学学习能力。依据学生认知特点、学习特点，把几何推理能力培养分为萌发期、发展期、提高期三个阶段。专题型微课可以在几何推理能力培养的三个阶段进行应用，帮助学生提高逻辑推理能力，拓展数学思维。

一、专题型微课在几何推理萌发期中的作用

1.培养直观实验动手操作能力

低年级学生的年龄较小，几何推理能力较低，数学认知结构水平有限，所获得的知识系统性弱、结构性差。因此，在几何推理能力萌发期，重视学生动手实验操作，通过看一看、量一量、做一做的直观实验来进行推理和判断，通过引导，不断培养学生的直观感知，从而提高对图形的直观推理能力。

教师在课堂上组织学生进行实验、尝试、观察、类比等合情推理的实验活动时，由于课堂时间有限，每个学生的认知基础、动手能力、观察能力和理解能力不同，在同一实验活动中获得的数学体验及对知识的理解也不尽相同。专题型微课可以在课后补偿性学习中弥补这个不足，微课可再现实验操作过程，学生可通过微课视频学习同时进行动手操作。微课具有暂停、快进、重复等功能，不同学生可以根据自己的实际情况重复使用，加深对知识的理解。同时，微课还可以作为课堂内容的延伸，针对课堂学习内容设计不同难度的问题，供不同层次的学生学习。例如，在七年级上册学习“长方体展开图”时，微课可以通过动画演示十一种侧面展开图的情况，学生可以跟着学习视频把一个盒子同步拆解，在动手实验过程中领悟由立体图形到平面图形的转化，各种展开图之间的区别以及其中蕴含的规律。微课可以开展拓展性学习，对学习能力比较强的学生，可让其根据微课学习收获设计制作长方体形状的包装纸盒，以提高学生动手能力，培养几何直观思维，对数学知识进行深度探究。

2.培养严谨的数学语言表述能力

在几何学习中，文字语言、图形语言、符号语言这三种语言是培养学生几何推理的基础。课堂上通过教师的引导，让学生明确如何将文字语言转化为几何符号语言，训练学生看图识图的能力，“图形+文字”转换为“几何符号”进行严谨的推理过程的证明。在教学中，教师注重几何语言规范和板书规范，促使学生养成良好的几何文字语言的严谨性，为培养几何推理打下扎实的基础。

学生学习能力不同，在课堂上对几何推理过程的掌握情况也不尽相同。专题型微课每节课针对一个小知识点展开学习，包括设置问题情境提出问题、引导分析问题、解决本微课的问题、方法与规律的归纳、迁移应用等五个环节。学生可以通过微课学习补上自己知识上的缺漏，规范书写格式，学会分析问题的方法，总结解题经验，然后通过微课同步变式练习进行迁移应用，形成数学学习能力。几何推理要求言之有据，每一步证明过程都有公理、定理、性质作为依据，学生在几何推理的萌发期对此不是很重视。微课可以通过在视频中设置动画提示、填空、小游戏等形式，让学生重视推理过程要有理有据，理解几何推理的严谨性。

二、专题型微课在几何推理发展期的作用

在几何推理的发展期，学生随着年龄的增长，其逻辑推理能力和理解能力进一步增强，教材的内容由研究点、线、角等基本图形向三角形、四边形、多边形等较复杂的图形发展，同时，此阶段出现添加辅助线解决问题等高阶思维，对学生的空间想象能力、逻辑推理能力、模型意识等数学能力提出了进一步要求，增强了对综合能力的考查。

1.培养几何模型意识

《义务教育数学课程标准》（2011 年版）提出“应当注重发展学生的模型思想”，数学模型思想的培养有助于学生应用能力、创新能力的提高。在教学中，基本概念、定理、性质等都是基本几何模型，在学生的认知基础上，为了便捷研究相关问题，在基本模型基础上提炼出更复杂且具有某种结构特征的模型，例如“一线三等角”模型、正方形“十字架”模型、“将军饮马问题”等。初中数学的教学一定程度上就是模型教学，一个个有序、完备的模型体系构成了数学的知识网。每一个模型的建立都对应着一个知识模块，而模型内部建立了知识模块之间的联系，从而让数学知识成为一个有机整体。专题型微课把基本模型设计成系列微课，让基本模型系统化、有序化、整体化。学生根据自己的学习情况自由选择，强化模型意识，提高解题能力。

3.发展中国家应对BEPS的弱征管能力寻求中国的帮助。BEPS是全球化深入发展的产物，AP-BEPS是多边框架，实施AP-BEPS，需要发展中国家参与共同协力合作，才能形成全球税收征管合力，维护发达经济体和发展中经济体的税收利益。发展中国家征管基础薄弱，应对BEPS的征管能力相对较弱，AP-BEPS的实施成本较高，迫切需要中国等新兴市场经济体帮助其征管能力建设，切实提高其应对BEPS的征管能力。

例如，“将军饮马问题”系列微课做出了如下设计（如图1）：

图1

学生通过系列微课的学习，掌握求最短路径的各种情况，对于符合基本模型的图形求线段和、三角形、四边形周长都有深入学习，在完成基本模型学习后进行综合应用，完成数学能力的迁移和应用。

2.变式教学拓宽思维的深度和广度

在专题型微课中使用变式教学，以三维目标为导向，有目的、有计划地对数学命题进行合理转化，不断更换命题中的非本质特征，促使学生掌握数学对象的本质属性，最终使学生透过现象看到数学知识的本质，同时，通过对数学问题的多角度、多方位、多层次讨论和思考，培养学生的数学思维品质。变式教学中使用一题多解、一题多变、一法多用和一题多用等变式，拓宽学生思维的深度和广度，促进学生的深度学习。专题型微课把综合性较强的题目进行分解，对题目涉及的重要知识点进行分课时讲解，同时对题目进行改编，通过变式展示知识发生、发展、形成的过程，从而让学生理解知识的来龙去脉，形成知识网络，使学生抓住问题的本质，加深对问题的理解。

例题：如图2，已知在等边三角形ABC 中，点O 为BC 边上任意一点，点D 在AC 的延长线上，且OA=OD,求证：AD=AB+OB。

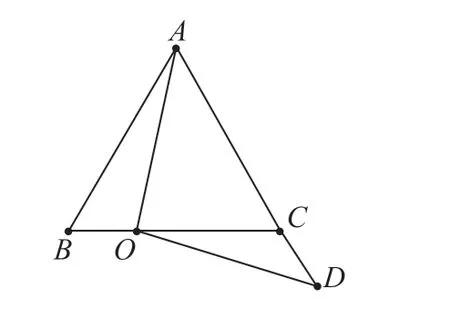
图2

这道题综合性比较强，需要添加平行线构造等边三角形或者用截长补短法来解决问题。我们把这道题设计三个课时的微课，让学生从这道题中更深刻地理解平行线构造等边三角形和截长补短法的应用。

第一课时：平行线构造等边三角形，共九种方法（如图3）。

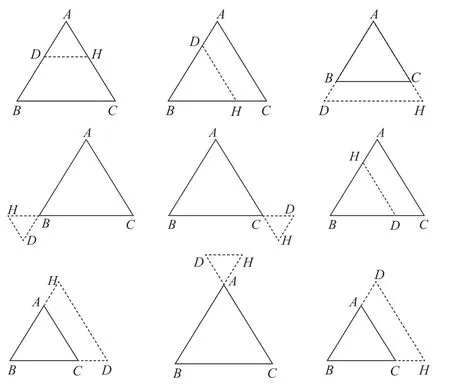
图3

第二课时：截长补短法构造等边三角形，共六种方法，如图4。

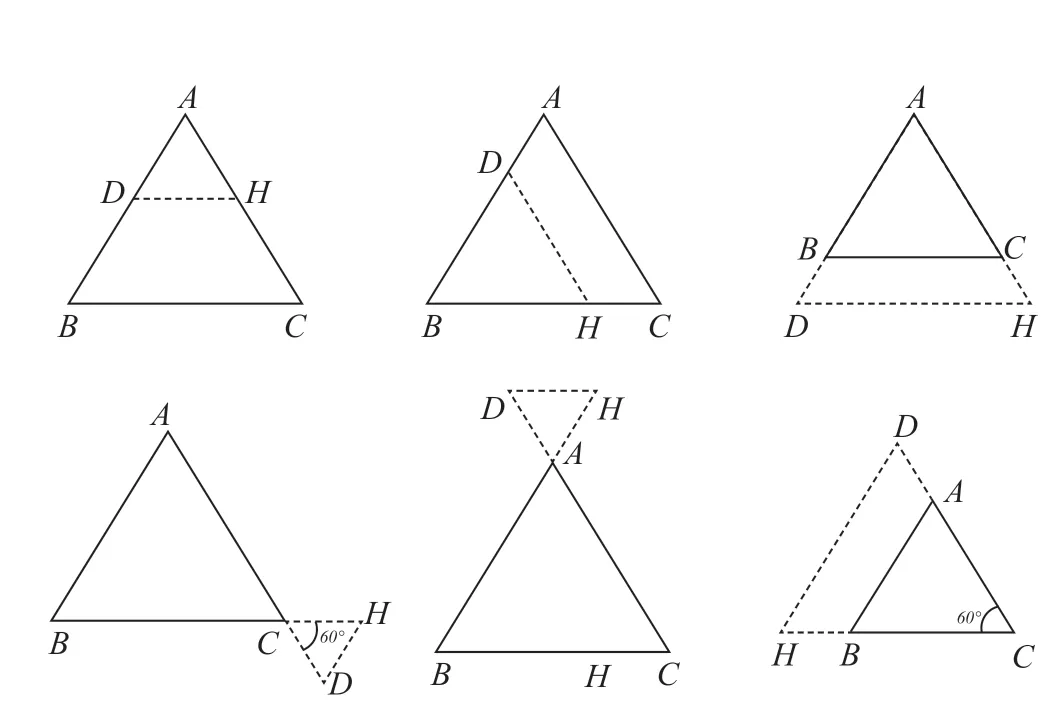
图4

第三课时：构造等边三角形综合应用。

由于有前两个课时的铺垫，这道题用构造平行线或截长补短法就有八种不同的解法，如图5。

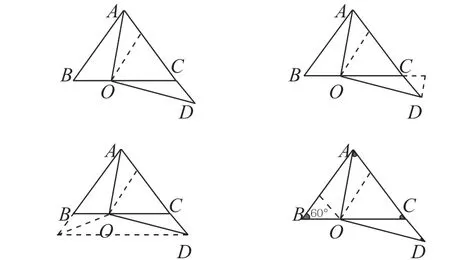
图5

同步变式：

已知△ABC 为等边三角形，AD=DE。

（1）如图6，当点D 为线段BC 上任意一点，点E 在AC 的延长线上时，线段BD、AB、AE 有何关系？请证明你的猜想。

（2）如图7，当点D 在线段CB 的延长线上，点E 在线段AC 上时，线段BD、AB、AE 有何关系？请证明你的猜想。

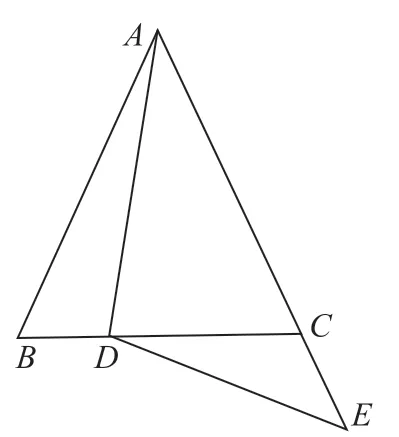
图6

图7

三、专题型微课在几何推理提高期的作用

在几何推理的提高期，专题型微课注重培养学生的几何结构关联推理和形式逻辑推理，能识别不同图形的特征和相关图形间的关系，能从复杂图形中找到基本图形和基本模型，接受其内在隐含的关系。专题型微课注重引导学生通过几何结构关联推理，寻找出整个推理方向和推理思路，熟练地运用形式逻辑进行表达，完成几何证明的全部过程。在初三的总复习中，通常一道综合性较强的压轴题涉及的知识点较多，图形较复杂，常常是基本模型的叠加，专题型微课注重引导学生识别其中的基本图形和模型，同时把题目中涉及的知识点设计成系列微课，搭建知识框架，完善知识体系，最后设计同步变式，完成知识应用和迁移。

例如：（2017 年南宁市中考题第25 题）如图8，AB 是⊙O 直径，弦CD ⊥AB，垂足为H，连接AC，过 上一点E 作EG ∥AC 交CD 的延长线于点G，连接AE 交CD 于点F,且EG=FG，连接CE。

（1）求证：△ECF ∽△GCE；

（2）求证：EG 是⊙O 的切线；

此题涉及知识点包括：垂径定理、三角形相似、平行线的性质、圆的切线、锐角三角函数的应用。

专题型微课设计如下：

（1）就这道题涉及的知识点，设计5 个系列微课，每一个知识点可以设计一节微课，搭建知识框架，完善知识体系，培养学生的应用意识，加深对知识的理解。

（2）设计系列同步变式训练：

在学生几何推理能力的培养中，专题型微课遵循学生心理、智力的发展特点，循序渐进地强化几何知识的学习，让学生在学习中获得成就感，激发他们的探究欲望，促使全体学生几何推理能力的提高。在系列微课设计中注重以“问题解决”为核心及数学思想方法的渗透，培养学生数学核心素养。