基于数学核心素养的高中教学实践研究

陈婉玲

[摘  要] 以“三角函数”的教学为例，探究如何寻找数学课堂教学中培养核心素养的“生长点”.文章对课程标准的要求进行了分析，在此基础上提出以“合理情境”来培养抽象思维素养;以“探究性活动”来培养直观想象素养;以“变式训练”来培养创新能力;以“归纳提炼”来培养归纳概括素养.

[关键词] 数学核心素养;三角函数;培养;新课程理念

在不断呼唤新课程改革的当下，课堂教学需摆脱传统教学中的“知识本位”和“教师本位”，让数学核心素养在教学实践的过程中自然落地. 由于数学核心素养具有“隐性”的特质，从而其发展需要内化在课堂教学之中自然渗透，这就需要我们在教学实践中时时刻刻关注到核心素养的落实，真正意义上寻找能培养核心素养的“生长点”. 本文以“三角函数”一节的部分教学片段为例，探究如何寻找数学课堂教学中培养核心素养的“生长点”.

以“合理情境”来培养抽象思维素养

在传统教学中，教师常常直接抛出定义，并以例题分析与讲解加以巩固而了事，从而使得教学效果不佳. 新课改风向标下，如何创设情境促使学生自主建构？如何培养学生的数学抽象素养？这些都需要教师独具匠心地进行教学设计，让课堂引入具有自身的特色和亮点，让探究活动顺理成章地自然展开，达到培养抽象素养的目的[1].

【教学片段1】

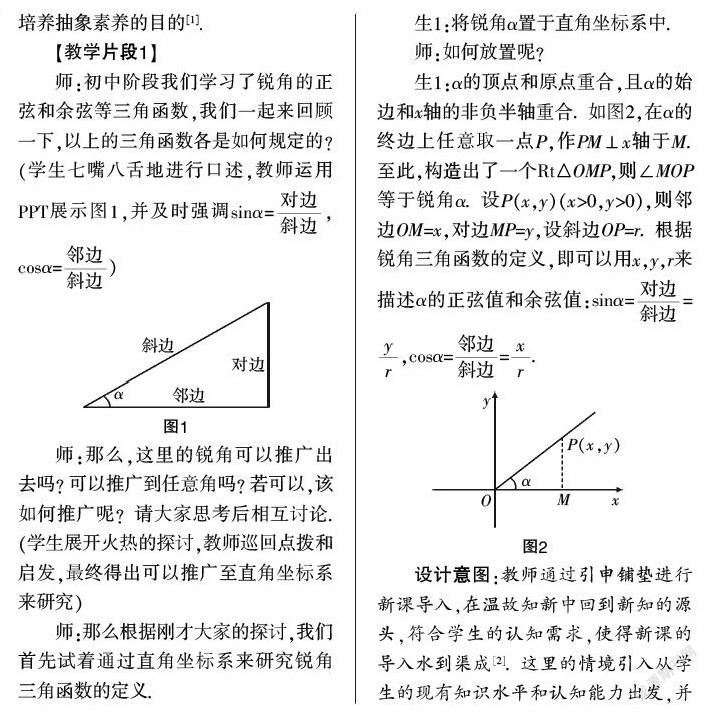
师：初中阶段我们学习了锐角的正弦和余弦等三角函数，我们一起来回顾一下，以上的三角函数各是如何规定的？（学生七嘴八舌地进行口述，教师运用PPT展示图1，并及时强调sinα=，cosα=）

师：那么，这里的锐角可以推广出去吗？可以推广到任意角吗？若可以，该如何推广呢？请大家思考后相互讨论.（学生展开火热的探讨，教师巡回点拨和启发，最终得出可以推广至直角坐标系来研究）

师：那么根据刚才大家的探讨，我们首先试着通过直角坐标系来研究锐角三角函数的定义.

生1：将锐角α置于直角坐标系中.

师：如何放置呢？

生1：α的顶点和原点重合，且α的始边和x轴的非负半轴重合. 如图2，在α的终边上任意取一点P，作PM⊥x轴于M. 至此，构造出了一个Rt△OMP，则∠MOP等于锐角α. 设P（x，y）（x>0，y>0），则邻边OM=x，对边MP=y，设斜边OP=r. 根据锐角三角函数的定义，即可以用x，y，r来描述α的正弦值和余弦值：sinα==，cosα==.

设计意图：教师通过引申铺垫进行新课导入，在温故知新中回到新知的源头，符合学生的认知需求，使得新课的导入水到渠成[2]. 这里的情境引入从学生的现有知识水平和认知能力出發，并及时进行必要的启发，引领学生进行自主探究和合作交流，实现了学生思维的“再创造”，有利于学生抽象思维的塑造.在整个过程中，以教师的提问为导向，通过观察、思考、分析、讨论，有效锻炼了学生的数学思维，学生共同体会运用坐标系进行研究的策略，实现认识的飞跃. 此处探究而得到的结论不仅包含了锐角三角函数的定义，同时也满足了任意角的情形，为后期更加深刻地理解和认识“任意角三角函数”的定义奠定了良好的基础. 当然，对于以上的课堂导入，倘若教师在细节处多一些雕琢，让提问更加富有创意，就更容易激起学生的探究兴趣，相信也能创造出更多的精彩生成.

以“探究性活动”来培养直观想象素养

直观想象素养是一种重要的数学思想和方法，利于学生运用空间想象能力思考问题的习惯的养成，利于学生更好地构建数学体系，利于学生论证数学概念能力的形成. 因此，教师不妨通过开展探究性活动，辅以动机诱导，将想象和探究的主动权交给学生，并对学生的大胆联想予以充分的肯定，对想象中合理的成分适时给予鼓励，进一步激发学生自发自觉地运用直觉思维去发现、提出、分析和解决问题，运用已有的知识与经验，插上“直观想象”的翅膀，使其放飞思维，自主构建新知.

【教学片段2】

问题1：既然角的概念已经推广开了，那么任意角的三角函数该如何定义呢？

师生活动：先让学生去想象和思考，使其得出主观性判断，再辅以几何画板演示，同时让学生通过观察图形，形成一定的认识.

问题2：大家一起思考，如何能让探究所得的定义式更加简洁？

师生活动：呈现问题的同时，以多个问题的铺开来引导学生进行讨论，最终引入单位圆.

问题3：现在该如何完善其定义呢？

师生活动：在学生提炼得出定义之后，教师及时整理和提炼.

问题4：从定义出发，探求任意角α的3个三角函数值的本质是什么.

师生活动：从问题中获得感悟，同时凸显三角函数概念的本质.

设计意图：探究活动是否能取得实实在在的成果已然成为探究性教学的主要追求.上述过程中，教师牢牢把握学生的知识水平，以发展学生的直观想象素养为核心出发，创设彼此关联和螺旋上升的“问题串”，激活学生的思维，使其在探究的过程中积极思考、大胆想象，获得新知，形成感悟. 以上活动是学生自己的活动吗？学生都经历了探究和思考的历程吗？显然，在以上探究中，教师给予了学生独立思考的机会，为学生创造了自主探究和合作交流的过程，使其获得了一种良好的学习能力，有助于实现自我突破，同时实现直观想象素养的发展.

以“变式训练”来培养创新能力

思维的创造性是一种重要的思维形式，将激励学生思维的发散性、求异性和创造性贯穿于教学活动，不仅是新课程标准的要求，也是孕育核心素养的前提.数学教学中孕育着丰富的创新素材，教师需从数学学科本身的特点和数学规律出发，积极探索训练学生创新能力的方法. 因此，教师可通过变式训练来强化对核心概念的系统认识，来培养学生的创新精神.

【教学片段3】

例题：已知角α的终边经过点P，-，试求出角α的正弦值、余弦值和正切值.

变式1：试求出的正弦值、余弦值和正切值.

变式2：已知角α的终边经过点P（-3，-4），试求出角α的正弦值、余弦值和正切值.

设计意图：“一题多变”是沟通学生与素养之間的一座桥梁. 教师从简单问题入手，运用好变式训练让学生从定义出发探究不同情况下的三角函数值，在深化定义理解的同时强化定义应用与几何的关联，使学生进入创新思维的佳境.

以“归纳提炼”来培养归纳概括素养

从教学的终极目标来看，教师的教需要以促进学生主动地学来实现核心素养的培育和学生自主发展的目标.教学过程中，教师不可包办或代替学生的学，教师需要为落实学生数学思维的发展而教. 从而，探究学习的过程应该让学生来完成，归纳提炼的任务更应该让学生来完成. 只有这样，才能获得具有价值的数学结论，形成清晰而系统的知识体系，培养归纳概括素养.

【教学片段4】

问题1：请试着阐述如何利用单位圆得出任意角三角函数的定义.

问题2：请试着归纳一下在今天的学习中，我们利用定义解决了哪些问题.

设计意图：从认知的角度来看，学生自己总结和归纳得出的结论才是最富有价值的，也是知识生长的最佳方式. 从而在这个教学环节中，教师不能包办学生的学习，应该让学生去总结、归纳和提炼，更好地培养归纳概括素养.

总之，新课程理念下，教师的教需要落实在学生的学之上，需要学生积极主动地去掌握数学基本知识技能，发展数学思维，培养数学核心素养，使得各种关键能力得以充分发展[3]. 因此，教师需从传统教学中的错误教学理念中走出来，以学生的需要开展教学活动，积极寻找核心素养的“生长点”，与时俱进地改进数学课堂，让学生的思维更好地发展，让数学核心素养落到实处，让课堂教学更加有效，这样才能真正符合新课程理念的要求.

参考文献：

[1]  黄晓学，李艳利. 论数学教学设计的创意生成点[J]. 数学教育学报，2010，19（06）.

[2]  柯跃海. 高考数学试题情境的创设实践[J]. 中国考试，2020（06）.

[3]  卢娟，孙道斌. 在深度对话中让数学概念课教学走向本真——“§5.1定义与命题”教学实录与点评[J]. 中学数学杂志，2017（10）.

2466501186274