立足“以生为本”，丰富基本活动经验

杨争艳

[摘  要] 文章以“梯形（第一课时）”为例，通过对课例的分析，指出生本理念下的数学课堂应立足经验、以生为本、以学定题，增强学生对学习过程的体验，积累丰富的基本活动经验，促进“四基”和“四能”的真正发展.

[关键词] 以生为本;基本活动经验;教学新思考;梯形

智慧是浩瀚的大海，经验则是大海中无尽的浪花. 数学活动经验是学习的基础和目标，是激活直觉、孕育创新的源泉，对学生知识、方法、思想的同化意义重大. 由此，足以见得数学活动经验的重要价值，但遗憾的是大部分教师在数学课堂中更多的是关注知识的传授和方法的掌握，却没有关注到活动经验的积累，没有想方设法借力去唤醒和激活学生的已有经验，增强学生的学习体验，使得学生丧失了丰富数学活动经验的方法与途径. 显然，丰富数学活动经验的前提是教师智慧的教学. 基于此，笔者以“梯形（第一课时）”为载体，做一些分析与探讨.

立足经验：植入知识的“根”

从梯形概念的核心本质来看，对梯形本质的理解是本课教学的重点. 因此，让学生充分地回忆并感知梯形是新知学习的关键所在. 为此，笔者以“导学单”为引，引导学生自学. 笔者认为，无论是哪个图形的学习，在概念生成过程中，我们都应该让学生自主自发地类比其他图形，确立定义的标尺.

片段1：预学阶段，自主学习

问题1：梯形普遍存在于我们的生活中，请列举实例进行说明.

问题2：类比平行四边形的定义，借助已有学习经验，试着给梯形下定义.

问题3：请试着分类图1中的梯形.

问题4：请尝试将一个三角形变成一个梯形.

课始，教师开门见山地提出交流预学效果的要求，通过引导、鼓励、追问，学生得出以下解答：

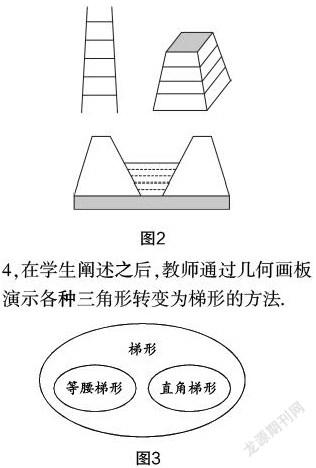
对于问题1，学生展示了图2所示的多种实例;对于问题2，师生共同类比归纳得出其定义、类型，更重要的是整理出图3所示的包含关系;对于问题3，学生分类如下：①⑥为等腰梯形，②④为直角梯形，③⑤为一般梯形;对于问题4，在学生阐述之后，教师通过几何画板演示各种三角形转变为梯形的方法.

设计意图  学生在小学阶段已经接触梯形的相关知识，教师设计导学单的主要目的在于唤醒学生的已有学习经验和知识经验，很好地类比平行四边形的学习过程，使得梯形概念、性质的理解和掌握相对流畅与自然. 问题1到问题3主要以问题的形式，让学生通过感知生活中的梯形及平行四边形的定义去认识梯形. 问题4通过动态演示梯形的形成过程，建构三角形与梯形间的桥梁，使其获得丰富的学习经验，从而为后续更好地抽象提供素材的助力.

思考  从实际效果来看，这样的教学设计从“数学源于生活”入手，再到类比表征梯形的概念和图形的演变，借助學生的已有生活经验和学习经验，帮助其建立清晰的梯形表象. 可以说，本环节已经达到笔者预期的效果，并为后续的学习确立了较为清晰的方向.

以生为本：深入知识之“本”

以学定教，自然需要首先考虑到“学”，只有充分把握“学”，才能让教师的“教”真正高效、流畅、自然. 于是，笔者基于研学的角度，以学生的生活经验为切入点，从动手操作这种接地气的探究方式出发，让学生自由表达对“梯形”的认识和理解.

片段2：动手研学，转化图形

请试着动手进行梯形的割补：

1. 经过梯形ABCD的一个顶点，将其切割为已学的特殊几何图形.

学生在动手操作之后，得出：如图4，过顶点A作DC的平行线与BC相交于点E，这样一来，梯形则被切割为平行四边形ADCE和三角形ABE.

2. 经过梯形ABCD的两个顶点，将其切割为已学的特殊几何图形.

操作之后，学生得出：如图5，分别过顶点A，D作AE，DF垂直BC于点E，F，这样一来，梯形则被切割为矩形ADFE、直角三角形ABE和直角三角形DFC.

3. 请试着用你喜欢的方法将梯形ABCD割补为已学的特殊几何图形.

一番操作之后，学生得出：如图6，连接AC或分别延长BA和CD相交于点E，这样一来，即可将梯形分割为两个三角形或补为一个三角形.

设计意图  本环节设计的主要目的是很好地融通三角形、平行四边形和梯形的相关知识，助力学生更好地理解梯形知识的本质. 这里教师通过引导学生动手操作，去作辅助线来转化梯形问题，达到感悟转化思想之效. 而这里转化思想的渗透相对来说十分重要，所以适时展开“梯形割补”的活动，不仅可以省去细究教材的麻烦，尽量避免了“简单的事情复杂化”，又可以借助于多感官的协同参与，让学生将课堂宝贵时间更好地用于获得活动经验之上. 教学中，笔者很好地渗透了转化思想，为后续“证明等腰梯形的性质”指明了思考的方向. 学生通过体验数学活动，进一步积累学习经验，最终完善和深化对“梯形”的认知.

思考  从这一环节的教学效果来看，学生参与的积极性十分高. 开展的探究活动不仅为学生的进一步学习提供了鲜活的生本资源，同时为其理性认识梯形提供了多元支持. 尤其是当完成这里的第3个问题时，学生水到渠成地感悟到转化的思想，从而为课堂鲜活的生成提供了更多可能.

片段3：猜想研学，合作提升

问题1：借助已有经验，并类比平行四边形的性质，你认为该从哪些方面探究等腰梯形的性质？

问题2：请试着从边、角、对角线、对称性这4个方面，类比猜想等腰梯形的性质，并填表.

问题3：通过小组合作学习的方式，验证以上猜想.

设计意图  通过数学活动设计，引导学生立足于数学角度进行深度思考，并借助以往的学习经验直观、理性地进行猜想，更进一步地通过几何画板验证猜想的正确性，最终获得简洁生动却又准确深刻的认知.

思考  由于在活动探究环节，学生充分感知了转化的数学思想，故在本环节中可以借助转化思想用于猜想和证明，以获得解决梯形问题的有效策略，从而让四边形的相关知识和研究方法具有全面性和系统性. 这里给了学生足够“宽”的时空，鼓励他们自主摸索，让他们充分体验新知的摸索之路，因此使得每个学生都能获得属于自己的数学活动经验.

以学定题：延伸知识之“里”

拓展阶段的学生对梯形已经有了一定的认识，基于此，笔者以类比探究为抓手，以学生的已有经验为落脚点，对课堂教学的延伸进行层层递进式的处理，努力延伸知识之“里”，使得学生在增长知识的同时实现思维能力的稳步发展.

片段4：探究验学，类比到底

问题：任意画出一个梯形ABCD，并连接其两腰中点E和F，则线段EF为该梯形的中位线.

（1）测量EF及AB，CD的长度，你发现它们之间有何关系？请说出你的猜想，并证明.

（2）根据猜想，你认为梯形面积计算公式可能简化吗？

（3）如果点E和F分别为梯形的两条对角线的中点，那么EF与AB，CD的长度又有何关系？

设计意图  设计循序渐进的探究活动，为学生营造一个主动运用新知解决新问题的情境，让学生在观察、猜想、证明、运用的过程中拓展知识、放飞自我，最终在领悟数学思想的同时，培养其推理能力，使得直观想象、归纳推理、演绎推理素养在这一系列的探究活动中得以发展，更重要的是积累了新的活动经验.

思考  从上述环节的教学不难看出，笔者以一个完整的探究活动为线索，展开了深度探讨，同时借助想象、推理等学习方式，实现了学生思维认识由“表面”走向“深刻”.

结论与思考

当然，“以生为本”理念下的数学课堂，除去促使学生获得丰富活动经验之外，教师还须重点关注对学生思维能力的培养. 总体来说，教师只有基于学生思维发展，从学生的已有学习经验、生活经验和知识经验出发，借助于丰富资源的支持，以探究性问题为引领，才能丰富学生的基本活动经验，真正意义上促进“四基”和“四能”的发展.

3479501908224