群智感知中基于时空关联性的用户激励机制
周 强,李 鹏,聂 雷
(1.武汉科技大学计算机科学与技术学院,武汉 430065;2.智能信息处理与实时工业系统湖北省重点实验室,武汉 430065)
0 概述
群智感知是结合众包思想和移动设备感知能力的一种新的数据获取模式[1],其通过移动设备形成交互式和参与式的感知网络,并将感知任务发布给网络中的个体或群体来完成,从而帮助专业人员或公众收集数据、分析信息和共享知识。相比传统固定基站的数据收集方式,一方面群智感知模式由于GPS、罗盘、加速计等大量传感器嵌入手机移动设备,用户可方便快捷地参与任务,另一方面在收集大规模和大容量数据时其在质量、速度和效率方面更具优势。本文以群智感知技术为研究背景,提出基于显性时空关联和隐性时空关联的用户激励算法。
1 相关工作
在用户激励机制方面,文献[2]主要从技术层面入手,分析激励机制中的影响因素。文献[3]研究跨空间领域中有关群智感知的用户激励机制、任务请求者以及最终执行任务的用户三者之间的关系和多元互动来激励效率高、质量好的用户参与群智感知任务。文献[4]在移动数据收集过程中设计一种基于时间敏感的用户激励机制,将用户激励问题转化为用户博弈问题,并证明了该博弈满足纳什均衡理论。
在用户招募方面,文献[5]从用户社交性以及用户和感知目标的距离角度进行群智感知用户招募。文献[6]对具有最低花费且用户轨迹覆盖相关兴趣点的用户进行招募,且将招募问题转化为集合覆盖问题。文献[7]建立用户质量模型、估算用户信誉模型来选择高质量用户,且利用沙普利值计算用户酬劳。
在用户时空性方面,文献[8]不仅考虑用户当前位置,而且考虑用户未来轨迹,将用户选择问题转化为NP-Hard 问题并提出贪婪算法进行求解。文献[9]结合感知任务的空间性和移动用户的时间性提出LRBA 算法,从而将整个任务分配问题划分成若干个子问题。文献[10]研究基于感知任务截止时间的用户选择问题,并证明该问题是NP-Hard 问题。文献[11]将感知任务分成时间敏感和延时容忍任务,对于时间敏感任务,招募用户的准则是最小化用户移动的总距离,而对于延时容忍任务,尽可能减少招募的用户数量。文献[12]提出一种依赖时间窗口和对数据完整性有较高要求的激励机制,使用反向拍卖的框架来建立系统模型。
在预测用户时空性方面,文献[13]通过半马尔科夫模型[14]预测兴趣点轨迹,并充分考虑时间和空间的因素对用户进行选择。文献[15]分析用户完成任务的数量,根据用户上传数据的方式不同(蜂窝网络和WiFi网络),通过马尔科夫模型对用户轨迹进行预测,设计相应的贪婪算法进行满足预算限制和最佳用户的招募。文献[16]针对确定轨迹和不确定轨迹分别提出基于线性规划的遗传算法和贪婪算法,并且保证了算法有效性。文献[17]建立基于兴趣点的轨迹预测模型得到所有任务的完成概率,并提出离线贪婪算法和在线用户招募算法。文献[18]基于群智感知提出实时轨迹追踪系统,实现最大化实时追踪轨迹和真实轨迹的覆盖,并且最小化参与实时轨迹追踪系统的用户数量。
上述传统激励机制未同时考虑时空及时空关联性因素,因此造成很多感知任务难以执行。基于时空因素,文献[19]采用深度学习模型,提出基于时空相关性的短时交通流量预测法,但该方法更多关注显性关联性。文献[20]研究时空因素下的用户招募和激励机制,但未考虑时空重叠和关联性问题,而对比传统激励机制发现,很多任务和用户具有时空重叠和关联特性。为解决感知任务完成率低且花费高的问题,本文提出基于时空关联性的用户激励机制STIM。
2 时空关联模型及问题定义
2.1 系统模型
假设系统中发布一系列群智感知任务S={S1,S2,…,Sm},对于任意任务Sj∈S均存在时间范围和空间范围Pj={l1,l2,…,lm},其中表示感知任务的开始时间表示感知任务的结束时间,lm表示感知任务需要感知的路段。结合时间和空间范围,通过二元组,{l1,l2,…,lm} }来表示任务时空要求,即在时间范围内经过的路段,例如θ1={[7:11],{l1,l2}}表示任务1 需要用户从07:00 到11:00 经过l1、l2两个路段。
假设系统有一系列用户U={U1,U2,…,Un},对于任意用户Ui∈U均存在用户三元组ωi=,{l1,l2,…,lm},ci},其中表示用户能参与任务的开始时间表示用户能参与感知任务的结束时间,ci表示用户花费,例如ω1={[7:11],{l1},10}表示用户1 从07:00 到10:00 经过l1路段,花费为10。
2.2 显性时空关联模型
显性时空关联表示感知任务与感知任务、用户与用户间存在相同时空特性,因此分别定义基于感知任务和用户的显性时空关联。
定义1(基于感知任务的显性时空关联)对于任意两个任务Sj1,Sj2∈S,满足时空重叠(见式(1)),则称该感知任务集合是基于感知任务的显性时空关联。
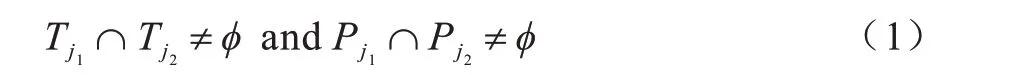
对于任意两个任务Sj1,Sj2∈S,满足时空重叠和时空覆盖(见式(2)),则称该感知任务集合是基于感知任务的覆盖显性时空关联。可见,时空覆盖任务一定是时空重叠任务,但是时空重叠任务不一定是时空覆盖任务,即时空重叠包含时空覆盖。
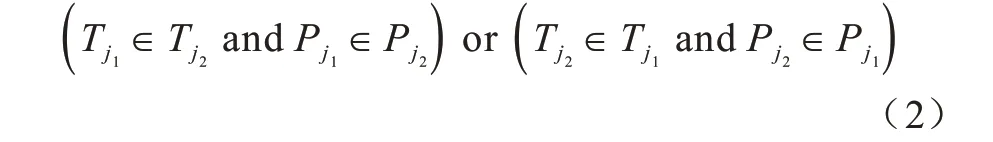
将所有基于显性时空关联的感知任务集合视为一个感知任务,用户的时空集合可以同时满足多个任务的时空需求,大幅提高运算效率。
定义2(基于用户的显性时空关联)对于任意两个招募用户Ui1,Ui2∈U,可能存在部分相同的时空集合(满足式(3)),则称有相同时空的用户集为基于用户的显性时空关联。

通过式(4)得到相同时空集合{[t′,p′]},并将用户集中有相同时空集合视为同一时空集合,这样模型只要支付一次该时空集合的花费,就能节省总花费。

图1 表示显性时空关联状态。已知感知任务1~感知任务4,感知任务1的感知时间间隔为08:00—10:00、感知任务2 的感知时间间隔为09:00—11:00、感知任务3的感知时间间隔为01:00—03:00、感知任务4的感知时间间隔为01:30—02:30;感知任务1和感知任务2的感知区域有重叠部分,感知任务3 的感知区域完全覆盖感知任务4 的感知区域。用户A 在时间间隔08:00—09:00 内停留在感知任务1 的感知区域、在时间间隔09:00—11:00 内停留在感知任务2 的感知区域。用户B 在时间间隔08:00—10:00 内停留在感知任务1 的感知区域、在时间间隔10:00—11:00 内停留在感知任务2 的感知区域。

图1 显性时空关联状态Fig.1 Dominant spatial-temporal association status
感知任务1 和感知任务2 是基于感知任务的显性时空关联,因为感知任务1 和感知任务2 有重叠时间,重叠时间间隔为09:00—10:00。另外,空间重叠为阴影部分,在任务发布后用户只需满足该部分的时空要求。感知任务3 和感知任务4 是基于感知任务的覆盖显性时空关联,因为感知任务3 覆盖感知任务4,所以发布任务后只需满足感知任务3 的时空要求。
用户A 和用户B 是基于用户的显性时空关联,如果只招募用户A,感知任务1 无法完成,如果只招募用户B,感知任务2 无法完成,为保证感知任务1、感知任务2 都被完成,任务发布者和参与用户所在的群智感知平台会同时招募用户A 和用户B。此时,在用户A 和用户B 的时空状态中存在重复的时空状态,即在时间间隔08:00—09:00 内用户A 和用户B 均停留在感知任务1 的感知区域、在时间间隔10:00—11:00 内均停留在感知任务2 的感知区域。
2.3 隐性时空关联模型
基于用户当前的时间和空间因素,用户仅参与其中某些任务,但是随着用户移动,用户的时间和空间因素会发生改变,此时用户可以参与一些额外任务。对于这种情况的用户,可以称为该用户存在隐性时空关联。在实际情况中无法知道用户未来移动方向,但是可基于用户之前移动情况进行预测,因此考虑马尔科夫模型得到用户在某一时间间隔内从一个路段l1移动到另一个路段l2的概率。
本文假设用户i的时空状态为Li={1,2,…,l},其表示用户当前所在的路段位置;表示用户i在第n个状态时的路段位置表示用户i在第n个时空状态时的开始时间,即用户i进入第n个路段的时间;表示用户i在路段的停留时间。
用户i在时间间隔t内从路段l1到路段l2的概率为:

如图2 所示,通过马尔科夫模型预测用户从路段l1移动到路段l2的概率,显示用户1 的历史时空状态信息,用户1在08:00到达路段,在10:00到达路段,……,在14:00 到达路段,在路段l1停留时间分别为{2,4,6,3,6}。因为从l1离开的路段总数为,从l1移动到l2的总数为,所以从空间上得到,时间间隔设置为4 h,10:00 和12:00 到达l2的时空状态满足该时间间隔,因此从时间上得到:
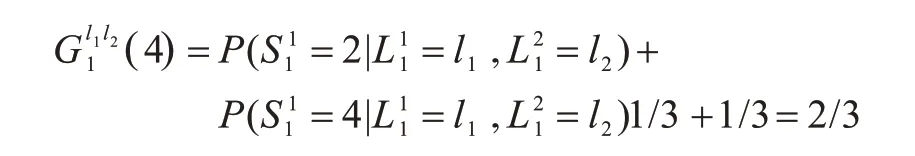
综合时间和空间因素,用户1 在4 h 内从l1到l2的概率为

图2 马尔科夫模型的预测过程Fig.2 Prediction process of Markov model

式(9)表示两个感知任务不存在任何显性时空关联,即两个完全独立的感知任务。式(10)表示用户i的第1 个时空信息三元组ωi可以参与任务j1,即满足第1 个感知任务的时空要求。式(11)表示ωi不满足第2 个感知任务ω′i的时空要求。式(12)表示用户i的第2 个信息三元组可以参与任务j2,即满足第2 个感知任务的时空要求。式(13)表示用户i在时间间隔内(第2 个感知任务开始时间与第1 个感知任务结束时间的差值),从路段Pj1移动到路段Pj2的概率需要大于设定的阈值α,只有满足该条件,马尔科夫模型预测用户i的时空状态才能被认为是相对准确的。
隐性时空关联状态如图3 所示。目前已知感知任务1 和感知任务2,感知任务1 的感知时间间隔为01:00—03:00、感知任务2 的感知时间间隔为04:00—06:00;用户A 在感知时间间隔01:00—03:00 内停留在感知任务1 的感知区域,通过预测1 h 后的时空状态得到用户A 在感知时间间隔04:00—06:00 内停留在任务2 的感知区域。
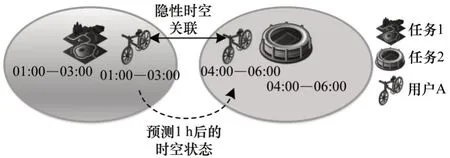
图3 隐性时空关联状态Fig.3 Recessive spatial-temporal association state
由于用户A 为隐性时空关联,因此用户A 的时空状态满足感知任务1 的时空要求,通过预测1 h后用户A 的时空状态,用户A 还可以完成感知任务2的时空要求,存在有效预测的时空状态,即在感知时间间隔04:00—6:00 内停留在感知任务2 的感知区域。
2.4 最大化社会收益问题模型
定义4(用户收益)群智感知平台给用户的报酬与用户参与任务的花费之间的差值即为用户收益ui,即:

对于所有感知任务,如果用户一个感知任务都没有完成,则表示用户没有参与任何感知任务,收益为0,xij=0 表示用户i没有参加感知任务j,xij=1 表示用户i参加感知任务j。如果用户完成任务,则有相应收益,pi表示平台给用户的报酬,cij表示用户i参与任务j的总花费。
定义5(社会收益)社会收益包含平台收益和用户收益,即:

其中,vj表示平台收益。可以发现平台给用户的报酬被抵消,因此得出社会收益由平台收益和用户参与任务的花费之间的差值所决定。社会收益越大,平台和用户会获得更多的收益,双方会更加有动力去完成群智感知任务,有利于平台对于优质用户的激励。
建立如式(16)所示的目标函数,考虑时空关联的情况下实现最大化社会收益并完成用户激励。
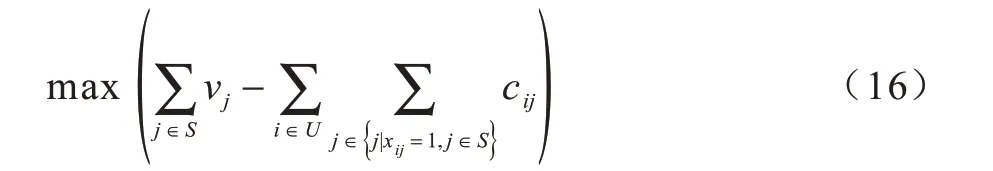
在所有感知任务发布确定的情况下,由于平台收益固定,即vj为固定值,因此为最大化社会收益,则需要最小化用户总花费。目标函数转化为时空关联情况下最小化用户总花费并完成用户激励:
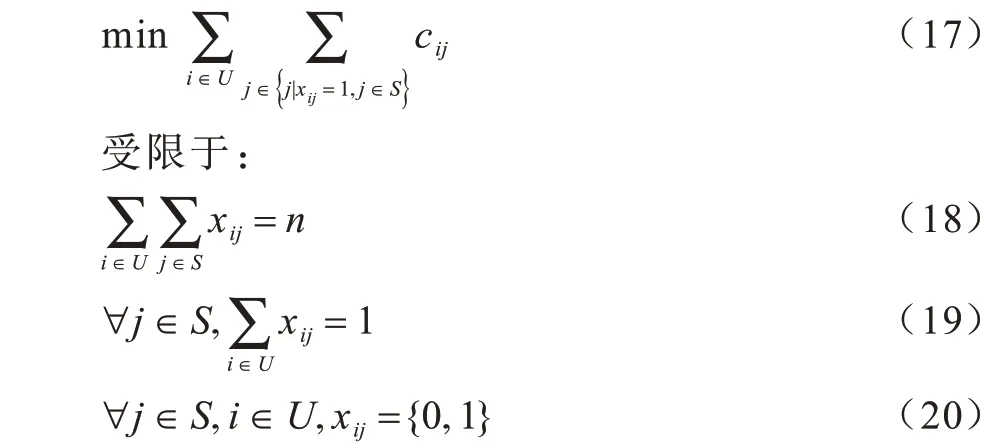
式(18)表示所有感知任务由用户完成;式(19)表示所有任务只能分配给一个用户完成;式(20)表示xij为0 或1,1 表示用户i完成任务j,反之用户无法完成该任务。如果是显性时空关联问题,则需满足式(1)~式(4);如果是隐性时空关联问题,则需满足式(9)~式(13)。
3 用户激励机制设计
定理1基于时空关联性的用户激励问题为NP-Hard 问题。
证明为证明STIM 问题是NP-Hard 问题,将该问题转化为传统最小化集合覆盖问题。因为最小化集合覆盖问题是NP-Hard 问题,所以STIM 问题是NP-Hard 问题。给定包含n个元素的总集合U和一系列集合U的子集S1,S2,…,Sk,并且每一个子集Sk都有花费Ck,为保证总集合U被全部覆盖,传统最小化集合覆盖算法最终选择总花费最小且集合覆盖个数多的子集,即。STIM 问题的给定情况为多个包含2 个元素(时间和空间)的感知任务总集合θ和一系列用户的时空集合ω1,ω2,…,ωk,其中用户集合包含3 个元素(时间、空间和花费),需要确保感知任务总集合θ被完全覆盖。为最小化用户花费,STIM 问题可转化为传统最小化集合覆盖问题,因此STIM 问题即为NP-Hard 问题得以证明。
3.1 基于显性时空关联的用户激励算法
由于STIM 问题是NP-Hard 问题,因此利用贪婪算法求解该问题。基于显性时空关联的用户激励算法DTS 如算法1 所示,贪婪策略的核心是最小化用户总花费和集合覆盖个数的比值,即
算法1基于显性时空关联的用户激励算法

以DTS 算法为例,已知感知任务的时空要求θ={{[1:2 ],{A} },{[2:3 ],{B}},{[3:4 ],{C}}},用户 1的时空集合为ω1={[1:2],{B},3},用户2 的时空集合为ω2={[2:3],{B},4},用户3 的时空集合为ω3={{[1:2],[2:3]},{A,B},5},用户4 的时空集合为ω4={{[2:3],[3:4]},{B,C},9}。DTS 算法得到结果为招募用户3 和用户4,最终总花费为9+5-4=10。因为用户3 和用户4 具有相同的时空状态,即用户2 的时空状态为ω′={[2:3],{B},4}。
3.2 基于隐性时空关联的用户激励算法
在解决隐性时空关联的用户激励问题时,考虑用户的历史时空状态以及用户当前提交的时空状态,利用马尔科夫模型预测用户的未来时空状态,再结合显性时空关联的用户激励算法得到最终结果。基于隐性时空关联的用户激励算法RTS 如算法2 所示。
算法2基于隐性时空关联的用户激励算法


以RTS 算法为例,已知感知任务的时空要求:θ={{[1:2],{A}},{[2:3],{B}},{[3:4],{C}}},用户1的时空集合为ω1={{[1:2 ],[2:3],[3:4]},{A,B,C},10},用户2 的时空集合为ω2={{[1:2 ],[2:3]},{A,B},5}。经过马尔科夫模型预测后得到最终结果为ω2={{[1:2],[2:3],[3:4]},{A,B,C},7}。因为预测的时空状态ω′={[3:4],{C},6},花费要比用户本身直接提供的时空集合花费低,所以RTS 算法得到的结果为招募用户2,总花费为7。
4 实验与结果分析
4.1 仿真数据设置
仿真数据实验时间序列列举24 h,即24 个点,空间序列列举26 个点。单一感知任务的时空要求分别从时间序列和空间序列中随机各取一个点构成,需要注意多个感知任务的时空要求不能重复,在此实验环境下最多产生24×26=624 个感知任务,因此选择400 个感知任务作为基数。单一用户的时空集合分别从时间序列和空间序列中各取一个点构成,时间序列先随机选中一个开始时间点,然后按照顺序选取1→2 →…→24 →1→2 →…→24;空间序列随机选取,为完成所有感知任务,最终选择10 000 个用户作为基数。设置一天工作时间为8 h,因此默认单一用户提供的时空集合数为8。预测概率阈值默认设置为0.80。本文实验采用单一变量法控制思想,在改变某一参数值的情况下,其他参数值皆为默认参数值。
本文提出的显性时空关联算法DTS 为执行MCO 算法后去掉重复的时空集合并减去相应的花费,隐性时空关联算法RTS 为经过预测得到预测时空集合后执行DTS 算法,其实验对比算法具体如下:1)最小化花费(Minimum Cost,MC)算法,每次选择花费低的用户;2)最大化覆盖(Maximum Overlap,MO)算法,每次选择时空集合覆盖最多的用户;3)最小化花费覆盖数比值(Minimum Cost Overlap,MCO)算法,每次选择花费和集合覆盖个数比值小的用户。本文实验对比参数为总花费、用户选择数和迭代次数,可变参数为感知任务数、用户数、单一用户提供的时空集合数和预测概率阈值。
4.2 仿真数据的实验结果分析
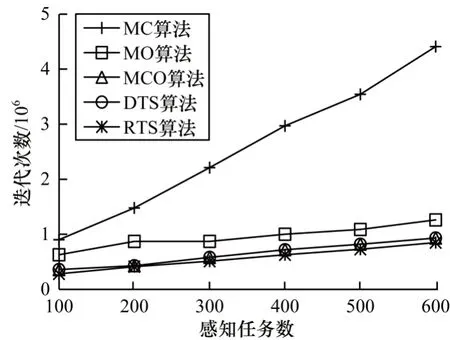
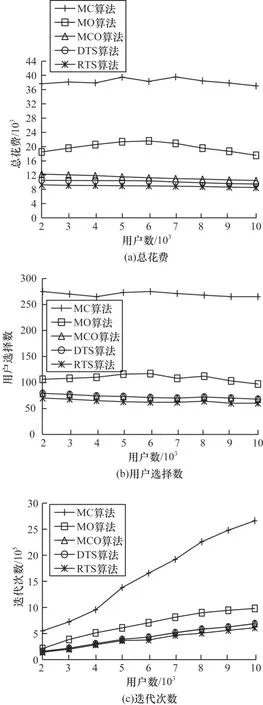
图4 表示感知任务数对总花费的影响。随着感知任务数的增加,5 种算法的总花费都增加,主要原因为平台需要招募更多的用户来完成更多的感知任务,所以总花费增加。对于总花费而言,算法顺序依次为RTS 图4 感知任务数对总花费的影响Fig.4 Impact of the number of sensing tasks on the total cost 图5 表示感知任务数对用户选择数的影响。随着感知任务数的增加,5 种算法的用户选择数随之增加,主要原因为平台需要招募更多的用户来完成更多的感知任务。对于用户选择数而言,算法顺序依次为RTS 图5 感知任务数对用户选择数的影响Fig.5 Impact of the number of sensing tasks on the number of user choices 图6 表示感知任务数对迭代次数的影响。随着感知任务数的增加,5 种算法的迭代次数随之增加,主要原因是为完成所有感知任务,平台需要招募更多的用户来完成更多的感知任务,所以相应算法的迭代次数会增加。对于迭代次数而言,算法顺序依次为RTS 图6 感知任务数对迭代次数的影响Fig.6 Impact of the number of sensing tasks on the number of iterations 图7 表示用户数对总花费、用户选择数和迭代次数的影响。总体而言,随着用户数的增加,5 种算法得到的总花费、用户选择数和迭代次数基本没有太大变化,大致呈现小幅度减少趋势,甚至有时出现总花费高、用户选择数多和迭代次数多的情况。其主要原因为平台发布的感知任务数已经固定,虽然用户数增加,但符合感知任务时空要求的用户数不一定再增大,反而会出现更多时空集合覆盖少、花费高的用户。因此,对于总花费和迭代次数而言,算法顺序依次为RTS 图7 用户数对总花费、用户选择数和迭代次数的影响Fig.7 Impact of the number of users on the total cost,the number of user choices and the number of iterations 图8 表示用户时空集合数对于总花费、用户选择数和迭代次数的影响。随着单用户时空集合数增加,用户选择数以及迭代次数持续减少,但是总花费持续增加,对于MC 而言,增大幅度最大,其主要原因为相对于单用户时空集合个数少的情况,MC 每次选择的用户是花费较高的用户(时空集合多且花费高),而且这些用户的时空集合中只有少部分符合感知任务的时空要求,因此MC 涨幅最大;DTS 和RTS基本保持不变,用户的时空集合多,总花费高。因此,对于总花费和迭代次数而言,算法顺序依次为RTS 图8 用户时空集合数对总花费、用户选择数和迭代次数的影响Fig.8 Impact of the number of user spatial-temporal sets on the total cost,the number of user choices and the number of iterations 图9 表示预测概率阈值增大对于总花费、用户选择数和迭代次数的影响。预测概率阈值的增大主要影响RTS 算法,可以看出其他4 种算法的预测概率阈值增大对于总花费、用户选择数和迭代次数的影响较小。随着预测概率阈值的增大,预测得到的用户时空状态集合越来越少,RTS 得到的结果越来越趋近DTS。因此,对于算法的总花费和迭代次数顺序依次为RTS 图9 预测概率阈值对总花费、用户选择数和迭代次数的影响1Fig.9 Impact of the predicted probability threshold on the total cost,the number of user choices and the number of iterations 1 真实数据集实验采用意大利罗马30 天内320 辆出租车的轨迹数据集[21],采集时间为2014 年2 月1 日至2014 年3 月2 日,约7 s 更新一次经纬度,数据格式为出租车ID、日期时间、经纬度。为更加契合仿真实验的参数设置,将罗马地区分为大小为100×100的网格,每辆出租车的轨迹经纬度转化为网格序号,表示出租车所在的空间范围;将每辆出租车进入和离开网格的时间表示出租车的时间范围。实验中用户数及单一用户提供的时空集合数为固定,因此改变感知任务数和预测概率阈值来验证算法的有效性,其他参数设置和仿真数据实验参数设置保持一致。 图10 表示感知任务数对总花费、用户选择数和迭代次数的影响。对比仿真数据实验结果,对于总花费而言,算法顺序依次为RTS 图10 感知任务数对总花费、用户选择数和迭代次数的影响Fig.10 Impact of the number of sensing tasks on the total cost,the number of user choices and the number of iterations 图11 表示预测概率阈值对总花费、用户选择数和迭代次数的影响。对比仿真数据实验的结果,除了总花费的影响外,其他没有太大变化,规律和逻辑都与仿真数据实验一致,随着预测概率阈值的增加,RTS 越来越趋近DTS。因此,对于总花费而言,算法顺序依次为RTS 图11 预测概率阈值对总花费、用户选择数和迭代次数的影响2Fig.11 Impact of the predicted probability threshold on the total cost,the number of user choices and the number of iterations 2 本文将时空关联的用户激励问题分为显性时空关联和隐性时空关联的用户激励问题,并提出RTS 算法和DTS 算法对其进行求解。通过仿真数据实验和真实数据集实验可以得出,RTS 算法和DTS 算法相比MC算法、MO 算法、MCO 算法具有更低的总花费、用户选择数和迭代次数,从而验证基于时空关联性的用户激励机制的有效性。然而本文在考虑隐性时空关联性时对于用户任务执行情况的预测存在不确定性,后续将对此做进一步研究,实现更高效的用户激励机制。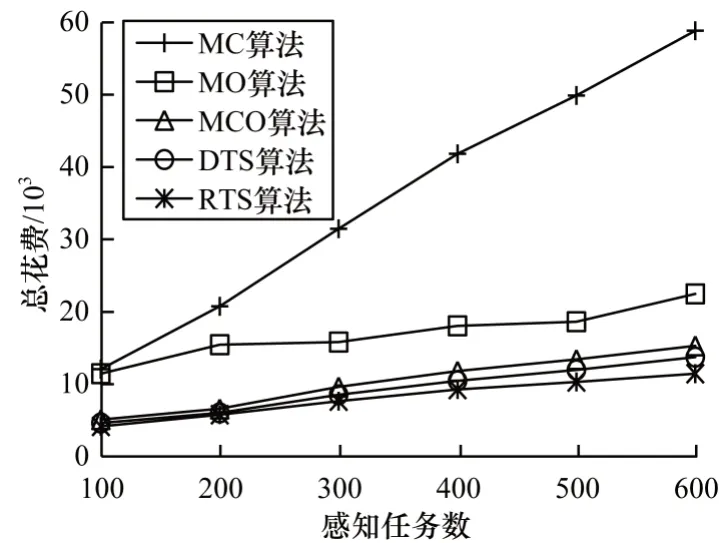



4.3 真实数据集设置
4.4 真实数据集的实验结果分析


5 结束语

