结合协方差与变异系数的密码芯片能量泄漏评估模型

蔡爵嵩，严迎建，朱春生

（战略支援部队信息工程大学密码工程学院，郑州 450002）

0 概述

侧信道分析技术［1］的提出为密码分析学开辟了一个新的研究领域［2-4］，但同时对密码算法的设计和实现提出了更高要求，使密码芯片安全性准则面临挑战。不同的算法设计使用的不同实现方式会使密码芯片在工作时泄漏不同程度的能量，这决定了整个密码系统安全性的强弱。因此，在利用侧信道分析技术对密码芯片进行安全性检测时，必须评估芯片工作时的能量泄漏情况。

在目前国际认可的信息技术安全性评估通用准则（Common Criteria，CC）［5］中，对芯片安全性的评定主要是利用所有已知的侧信道分析方法分析待测芯片，在此基础上对耗费时间、所用侧信道分析技术、芯片工作情况、特定有效时间以及所需要的软硬件等项目进行评分［6］。然而，该过程依赖于具体的侧信道分析方法评估芯片工作时的能量消耗及泄漏情况，不具备普遍性。现有关于侧信道能量泄漏检测的研究多使用t 检验［7-9］、连续互信息（Continuous Mutual Information，CMI）［10］和离散互信息（Discrete Mutual Information，DMI）［11］等方式进行，但都必须掌握芯片所使用的算法和实现方式。

本文对能量迹进行研究，通过结合协方差矩阵与变异系数，提出一种密码芯片能量泄漏评估模型。利用协方差矩阵［12］判断能量迹上各点的能量泄漏情况，在此基础上，通过引入变异系数［13］衡量矩阵内各元素的差异程度，从而评估能量泄漏程度。

1 基础知识

1.1 相关能量分析

相关能量分析（Correlation Power Analysis，CPA）［4］因简单有效成为侧信道分析中的一种常用方法，其基于芯片能量消耗和中间值模型之间的线性关系，通过计算两者的相关系数评估中间值模型与实际能量消耗的匹配程度。如果密钥猜测正确，则相关系数达到最大。

设W为芯片真实能量消耗值，H为猜测密钥对应的中间值，则两者的相关系数表示为：

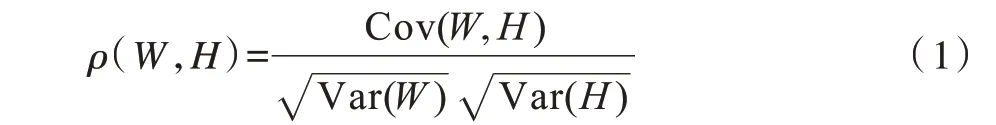
一般地，研究者采用的中间值模型为汉明重量（Hamming Weight，HW）模型或汉明距离（Hamming Distance，HD）模型。可通过式（1）计算猜测密钥对应的中间值与芯片实际能量消耗之间的相关系数，对应相关系数最大的密钥值即被认为是正确密钥。

1.2 协方差

在概率论和统计学中，协方差常用于描述两个变量之间的总体误差。假设X和Y为两个样本，则它们的协方差表示为：

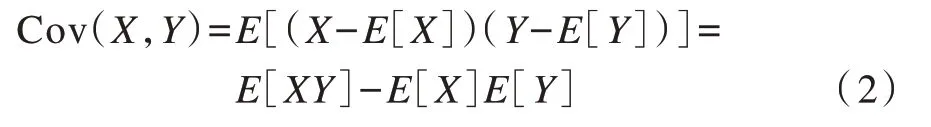
由式（2）可以看出，X和Y的协方差表示两个样本总体误差的期望，即X和Y偏离各自均值的程度。当Cov（X，Y）=0 时，说明X和Y不相关；当Cov（X，Y）＞0时，说明X和Y正相关；当Cov（X，Y）＜0 时，说明X和Y负相关。对于服从正态分布的X和Y，反之也成立，即：当X和Y不相关时，Cov（X，Y）=0；当X和Y正相关时，Cov（X，Y）＞0；当X和Y负相关时，Cov（X，Y）＜0。

在实际应用中，服从正态分布的X和Y对彼此的影响越大，表明X和Y的相关性越大，则Cov（X，Y）的绝对值越大。

1.3 变异系数

变异系数是概率论和统计学中评估总体中各样本差异程度或离散程度的指标，用于反映数据分布状况。当两组数据测量方式不同导致数据量纲不同时，研究者常用变异系数评估数据离散情况。对于一组样本数据，也可以用标准差来表示其数据离散情况，但当需要比较两组样本数据或多组样本数据的离散程度时，应当首先消除因测量方式导致的量纲不同所带来的影响，而通过变异系数即可达到此目的。变异系数定义为总体中各样本的标准差与其均值的相对数，计算公式如下：

其中，σ表示数据的标准差，μ表示数据的平均值。变异系数可消除因量纲不同而带来的影响，客观公正地对两组数据进行比较。

2 结合协方差与变异系数的能量泄漏评估模型

2.1 协方差在侧信道分析中的应用

一般地，研究者主要利用侧信道分析技术对芯片工作时的能量消耗进行分析。采集到芯片工作时的能量消耗，将所形成的曲线称为能量迹。一条能量迹上某点的能量泄漏定义为：

其中，Pop为与密码算法操作相关的能量消耗，Pdata为与数据相关的能量消耗，Pnoise为与噪声相关的能量消耗，Pconst为常量。

在一条能量迹中，各点的能量消耗是具有相关性的，对于此类关系可以进行可视化分析［14］。分别针对具有强相关性两点和具有弱相关性两点进行能量消耗关系的可视化分析，结果如图1 和图2 所示。可以看出，具有强相关性的两点能量消耗所形成的图形呈椭圆分布且数据点集中，具有弱相关性的两点能量消耗所形成的图形更接近于圆形且数据点分散。

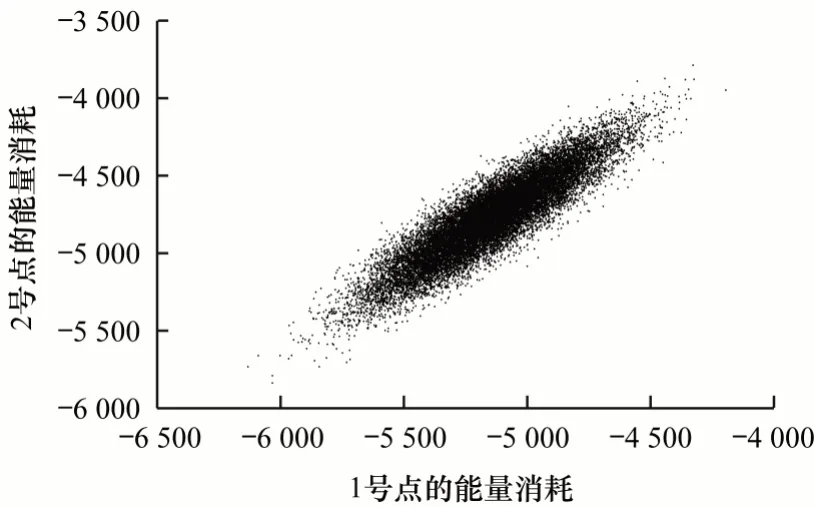
图1 具有强相关性两点的能耗散点图Fig.1 Scatter diagram of energy consumption for two points with strong correlation

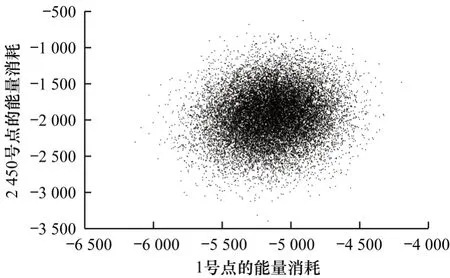
图2 具有弱相关性两点的能耗散点图Fig.2 Scatter diagram of energy consumption for two points with weak correlation

由1.2 节分析可知，可使用协方差来刻画能量迹上各点之间的相关性。因为在密码算法实现过程中，与密钥值相关的操作通常需要多个时钟周期，所以侧信道能量泄漏的点通常包含多个与目标中间值对应的样本点。一般将这些与中间值相关的点称为特征点PPOI。此外，根据Nyquist-Shannon 采样定律，信号采集设备的采样频率需要设置为芯片工作频率的数倍［15］。因此，每一个时钟周期即对应多个测量点。将测量点内除特征点PPOI以外的点称为非特征点Pelse。PPOI为能量迹上包含泄漏信息最多的点，Pelse为冗余无用的点［14］。

因为Pelse是信号采集设备为采集PPOI而出现的点，其各点间的相关性小于Pelse和PPOI之间的相关性，所以在计算特征点PPOI与非特征点Pelse的协方差时，表现为PPOI与Pelse的协方差远大于Pelse之间的协方差，即：

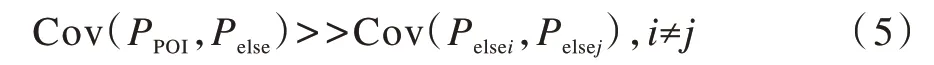
从侧信道分析角度来看，对协方差大的点进行分析，容易对芯片实施攻击，得到芯片密钥；而从评估芯片抗侧信道分析角度来看，如果从芯片泄漏的能量中能够明显找到协方差大的点，则表明该芯片抗侧信道分析的能力较弱，易于被攻击。因此，在对能量迹上各点进行能量泄漏分析时，可以关注是否有明显较大的协方差出现。

2.2 基于变异系数的能量泄漏评估原理

由式（5）可知特征点PPOI与非特征点Pelse的协方差和非特征点Pelse之间协方差的关系，据此得到如下推论：

推论特征点PPOI与能量迹上各点P（POI+else）的协方差之和远大于非特征点Pelse与能量迹上各点P（POI+else）的协方差之和，即：

证明：已知特征点PPOI包含最多能量泄漏［14］，以信息论中信号的方差表示信号的能量消耗，可得Cov（PPOI，PPOI）＞＞Cov（Pelse，Pelse）。由于特征点PPOI自身相关性必定远大于特征点PPOI与非特征点Pelse之间的相关性，即Cov（PPOI，PPOI）＞＞Cov（PPOI，Pelse），因此可得：

证毕。

在分析能量迹上各点的能量泄漏情况时，可以关注是否有明显较大的协方差出现。结合上述推论给出的关系，本文引入概率论和统计学中的变异系数，将求得的所有协方差组合成为协方差矩阵，通过计算变异系数得到各个协方差在矩阵中的分布情况，从而判断是否有明显较大的协方差出现。

在评估能量迹上各点的能耗泄漏程度时，将各点的协方差组成一个能量迹的协方差矩阵，通过计算该矩阵的变异系数判断能量迹的能量泄漏情况。若变异系数较大，则有明显的能量泄漏；若变异系数较小，则没有明显的能量泄漏。

2.3 能量泄漏评估模型

本文提出的能量泄漏评估模型，通过计算能量迹某点与能量迹各点的协方差之和，同时量化各点协方差的偏离情况来评估整条能量迹的能量泄漏情况。具体步骤如下：

1）采集大量能量迹，将能量迹集合表示为T=｛t1，t2，…，tn｝。其中，T为N×n的矩阵（N代表能量迹条数，n代表采样点个数），ti（i=1，2，…，n）为一个N×1的向量，表示这N条能量迹在相同位置i处采样点的值。

2）为减少协方差矩阵的计算量，对ti（i=1，2，…，n）进行均值化处理：

3）计算ti′和tj′之间的协方差：

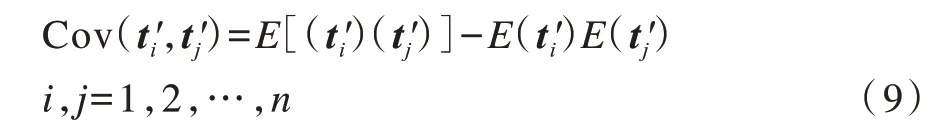
4）构建采样点协方差矩阵：

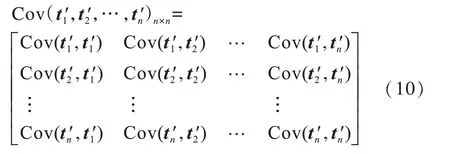
5）对协方差矩阵进行变换，得到S矩阵，本文将其定义为协方差行和矩阵，即：

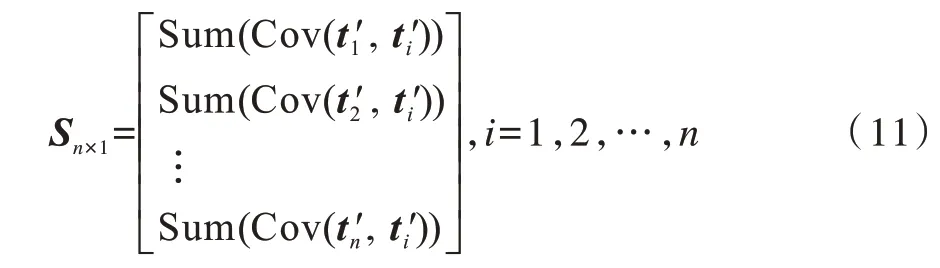
其中，Sum（Cov（tj′，ti′））表示N条能量迹中第j个采样点与能量迹各点之间的相关性。根据式（6）可知，若S矩阵中各个变量的值分布均匀，即无特别大的波动，则表示能量迹中各采样点的能量近似，没有特征点的存在，即没有明显的能量泄漏；若S矩阵中存在波动较大的值，则表示能量迹中各采样点的能量会集中于波动较大的点，即存在明显的能量泄漏。

6）计算协方差和矩阵S的变异系数，即：

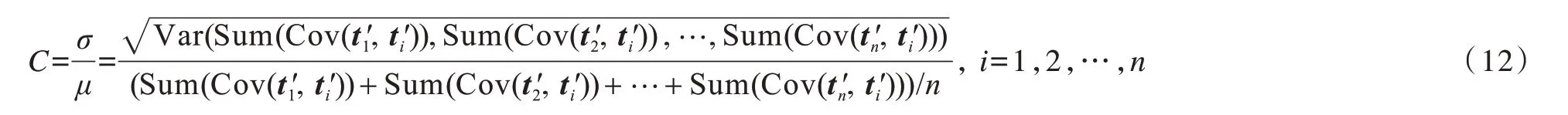
3 模型分析与攻击验证

本节利用2.3 节提出的能量泄漏评估模型对4 个数据集进行评估，具体步骤如下：

1）对协方差行和矩阵S进行可视化分析，验证使用S分析得到能量泄漏情况的合理性。

2）对变异系数进行分析，验证使用变异系数评估能量泄漏的有效性，即本文模型的有效性。

3）对数据集进行侧信道攻击实验，从攻击角度验证本文模型的有效性。

本文将第1 步和第2 步设置为实验1，将第3 步设置为实验2。

3.1 实验设置与数据集

3.1.1 实验设置

本文使用4 个数据集并设置两个实验对泄漏评估模型的有效性进行分析，将DPA contest v2［16］官方给出的能量迹作为数据集data1，将SAKURA-G 开发板［17］上采集的能量迹作为数据集data2，将DPA contest v4［18］的能量迹作为数据集data3，将基于ATMEGA2560 芯片开发板采集的能量迹作为数据集data4。

实验1对4 个数据集分别构建协方差行和矩阵S，并按2.2 节所述的可视化分析方法验证其合理性。在此基础上，分别求出变异系数Cdata1、Cdata2、Cdata3和Cdata4并加以分析，得到能量泄漏关系。本文在data1 和data2 上分析基于FPGA 不同实现方式的芯片能量泄漏情况，在data1、data2 和data4 上分析芯片串/并行的能量泄漏情况，在data1～data4 上分析芯片加入防护和未加防护的能量泄漏情况。

实验2对实验1 结果进行攻击验证。采用1.1 节所述的相关能量分析技术对data1、data2 和data4 分别进行攻击，以验证本文模型的正确性。

3.1.2 实验数据集

DPA contest v2 是2010 年由巴黎高科电信学院举办的侧信道竞赛，其提供了基于SASEBO-GII 开发板的能量迹，并分为1 个1 000 000 条的template 能量迹集和32 个20 000 条的public 能量迹集。其中，template 能量迹集，为随机明文和随机密钥，public 能量迹集为同一密钥下20 000 个随机明文。由于相关能量分析技术只能针对同一密钥、不同明文的情况，因此本文模型分析和攻击验证均使用public 能量迹集。与基于SAKURA-G 开发板的能量迹相比，两个数据集均为硬件实现的并行AES 算法的能量泄漏曲线，其不同在于DPA contest v2 中的S 盒实现为布尔函数法［19］，而SAKURA-G 中的S 盒实现为查表法［20］。

DPA contest v4 是2013 年由巴黎高科电信学院举办的侧信道竞赛，其提供了基于ATMega-163 的SASEBO-W 开发板的能量迹，并加入掩码，对一阶侧信道分析进行防护。基于ATMEGA2560 芯片开发板实现的AES 与DPA contest v4 相比，未加入任何侧信道防护措施，而与DPA contest v2 和SAKURA-G相比，使用串行实现方式。

3.2 泄漏评估模型验证实验

3.2.1 协方差行和矩阵的合理性验证

本节选取data1，计算该数据集的协方差行和矩阵Sdata1，并将其可视化，利用2.1 节中的相关性可视化分析方法，验证是否能够使用行和矩阵Sdata1来描述能量迹上某点与整条能量迹所有点之间的相关性。此处任意选取两个协方差行和矩阵中不同的两个点进行分析。data1 协方差行和曲线如图3 所示。

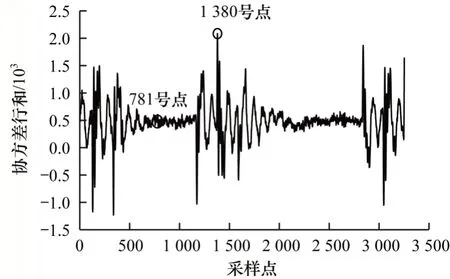
图3 data1 协方差行和曲线Fig.3 Covariance row curve of data1

从图3 可以看出，在data1 中，781 号点的协方差行和远小于1 380 号点的协方差行和。通过上文分析可知，1 380 号点与整条能量迹所有点的相关性大于781 号点与整条能量迹所有点的相关性。根据2.1节所述，选择3个点（1号点、700号点和1 300号点）对781号点和1 380号点分别进行相关性可视化分析。选点依据是选择两个分别为781 号点和1 300 号点附近的点，以及1 个离781 号点和1 300 号点距离都较远的点。

通过图4 和图5 可以看出，1 380 号点与能量迹上各点的能量消耗均呈椭圆分布，而781 号点与能量迹上各点的能量消耗更接近于圆形。根据1.3 节的描述可知，1 380 号点与能量迹上各点的相关性强于781 号点与能量迹上各点的相关性，与图3 描述一致，这说明通过协方差行和矩阵描述能量迹上某点与整条能量迹所有点的相关性是合理的。

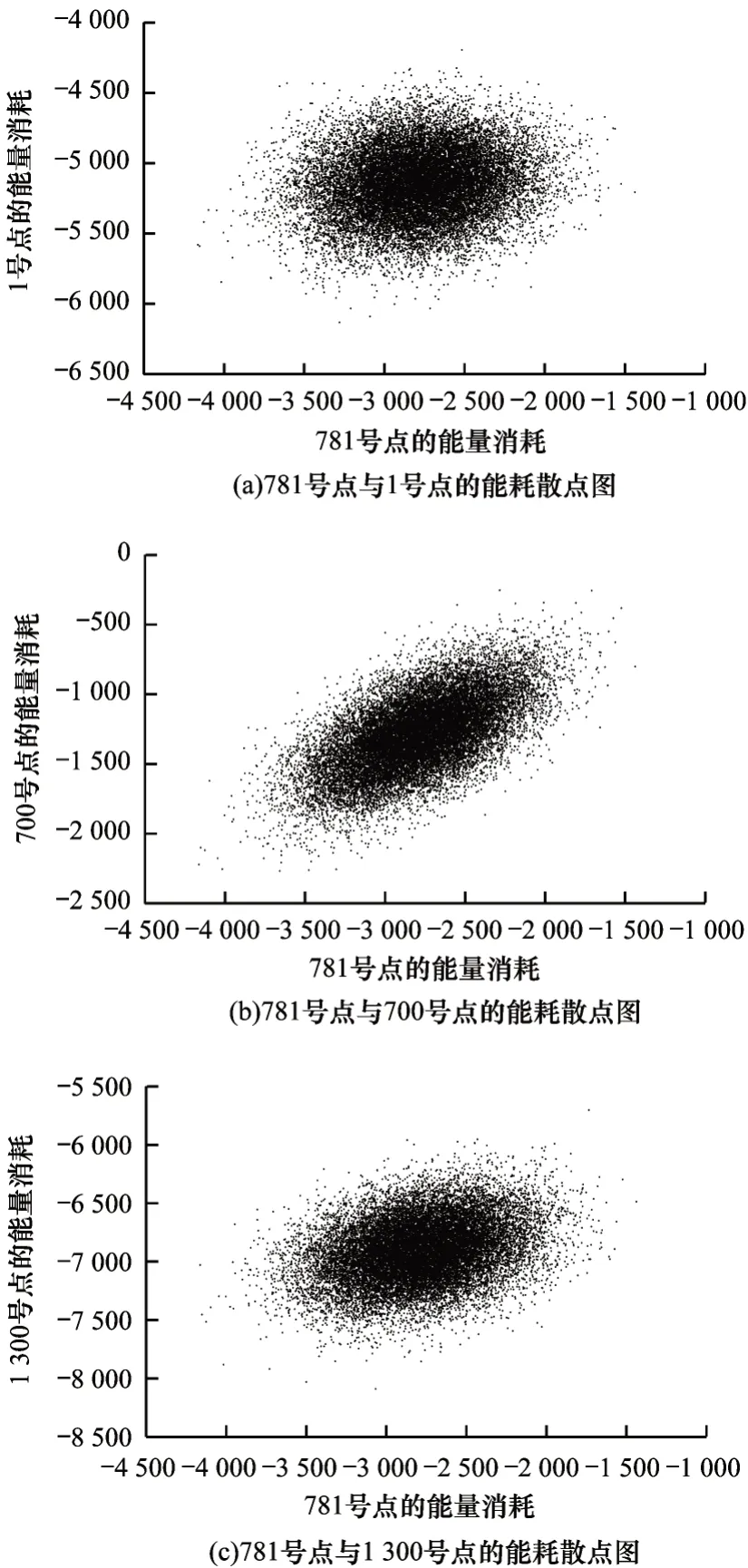
图4 781 号点与1 号、700 号、1 300 号点的能耗散点图Fig.4 Scatter diagrams of energy consumption for point 781 with point 1,point 700 and point 1 300

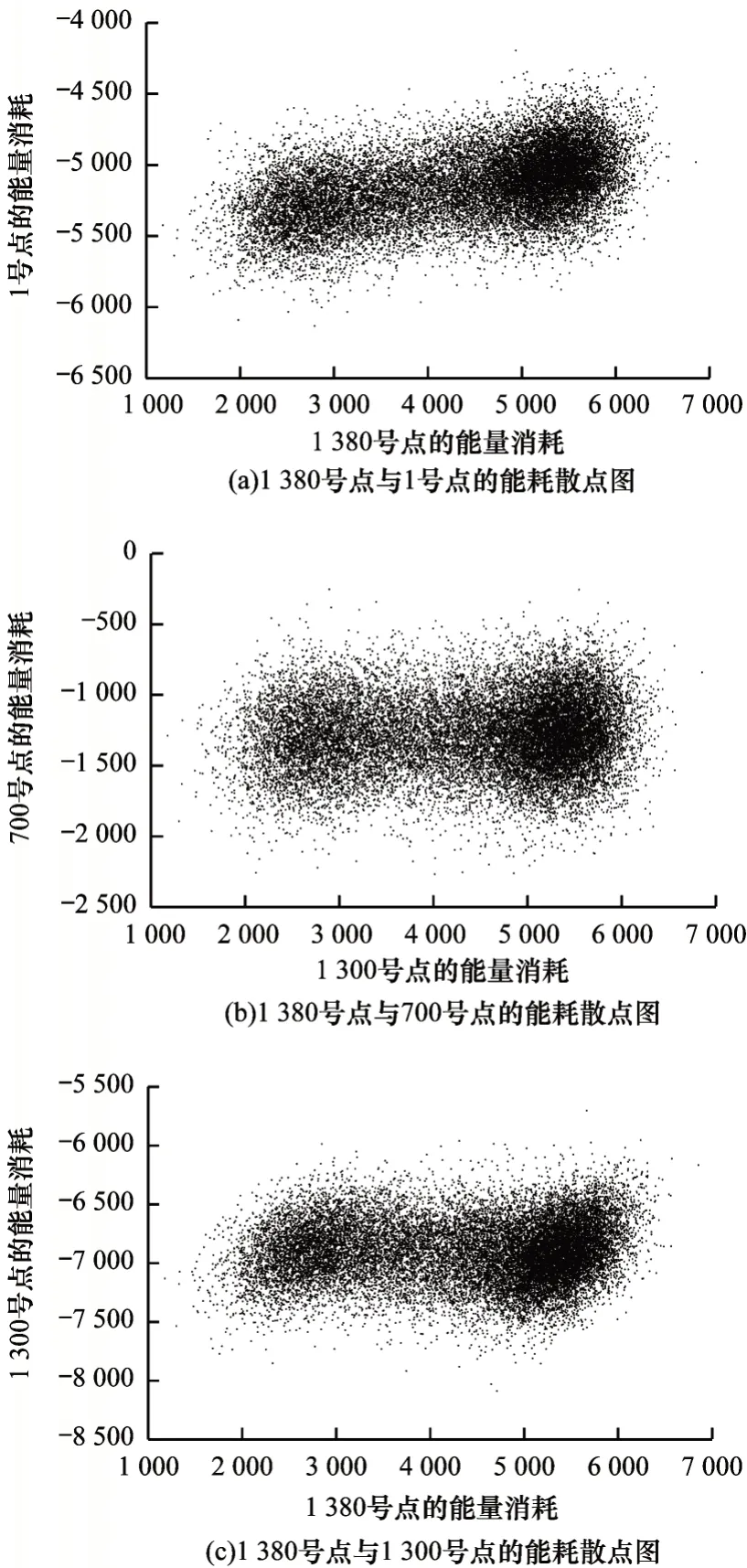
图5 1 380 号点与1 号、700 号、1 300 号点的能耗散点图Fig.5 Scatter diagrams of energy consumption for point 1 380 with point 1,point 700 and point 1 300

3.2.2 数据集变异系数分析

本文通过Matlab 实现2.3 节中的模型，分别输入data1～data4 得到变异系数Cdata1～Cdata4，如表1 所示。

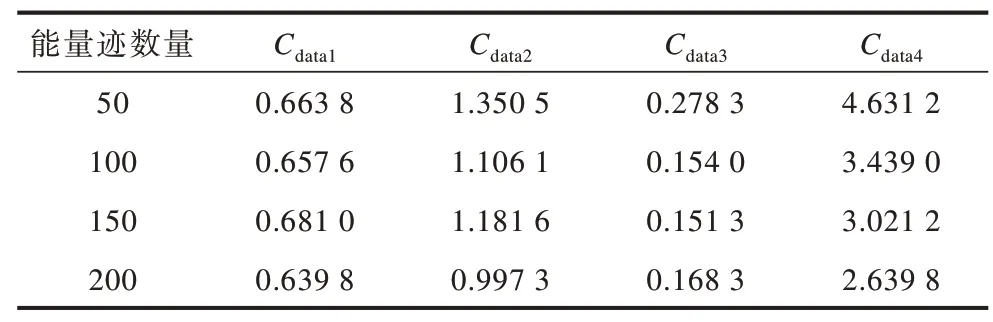
表1 4 个数据集在不同能量迹数量下的变异系数Table 1 Variation coefficients of four datasets under different energy trace numbers

从表1 可以看出，4 个数据集协方差行和的变异系数大小排序为Cdata4＞Cdata2＞Cdata1＞Cdata3。由2.2 节的原理分析可知：data1 中能量迹的能量泄漏小于data2中能量迹的能量泄漏，data1 和data2 的能量泄漏小于data4 的能量泄漏，data3 的能量泄漏为4 个数据集中最小的。下面对这一结论进行详细分析：

对基于FPGA 硬件实现的密码芯片而言，能量消耗分为动态功耗和静态功耗。芯片工作时，能量消耗以动态功耗为主，寄存器的变化是引起能量泄漏的主要因素。对AES 算法实现而言，寄存器的输入端都是一系列布尔函数的输出。data1 的S 盒为布尔函数实现，与其他操作的实现方式相同。当芯片工作时，所有操作引起的变化相同，所以就不存在明显的能量泄漏。data2 的S 盒为查表实现，并不会导致寄存器的变化，而算法的其他操作是基于布尔函数实现的，所以就会存在明显的能量泄漏。因此，data1 的能量泄漏小于data2 的能量泄漏。

对于芯片串/并行实现方式而言，串行实现的AES 算法每轮中的每个S 盒均有能量泄漏，则至少有16×10=160 个泄漏点存在，而并行实现的AES 算法每轮中的16 个S 盒均在同一个位置，即只存在16 个泄漏点。因此，data1 和data2 的能量泄漏小于data4 的能量泄漏。

对加入防护的芯片进行分析可知，加入防护的目的就是为了增强芯片的安全性，通过无效操作掩盖有效信息，减少芯片工作时能量泄漏包含的有效信息，因此，显然data3 的能量泄漏应该是最小的。

3.3 攻击验证

利用相关能量分析技术对data1～data4 数据集分别进行攻击来验证本文模型的有效性。攻击前对数据集中的能量迹进行对齐处理。

由于data1 和data2 数据集均为基于FPGA 硬件实现的AES 算法的能量泄漏曲线，因此模型选择为能够刻画寄存器值变化的汉明距离模型。初步选择能量迹数量为2 000 条，无法攻击获得正确密钥时，则增加能量迹条数，最多增加至20 000 条。

对data1 的最后一轮S 盒进行攻击，计算最后一轮S 盒的输入与密文之间的汉明距离同能量迹之间的相关系数。当能量迹数量为2 000 条时，无法攻击获得该轮子密钥；直到14 000 条时，攻击获得4 Byte 的子密钥。当能量迹条数达到最多20 000 条时，使用经典的CPA 攻击依然只能攻击获得4 Byte的子密钥。

对data2的第1轮S盒的输入进行攻击，计算第1轮S 盒的输入与上一轮密文之间的汉明距离同能量迹之间的相关系数。当能量迹数量为2 000 条时，使用经典的CPA 攻击便能攻击获得完整的密钥值。

对data4的攻击，中间值模型选择为汉明重量模型，计算第1 轮S 盒输出的汉明重量同能量迹之间的相关系数，只需要48 条能量迹便能攻击获得完整的密钥值。

由于data3 加入掩码防护，因此使用与data1、data2 和data4 相同的攻击方法无法对其进行攻击。

攻击实验结果表明，能量迹的能量泄漏从大到小依次为data4、data2、data1 和data3，与3.2.2 节分析结果一致，验证了本文模型的有效性。

4 结束语

现有芯片安全性评估标准依赖于具体的侧信道分析方法，并且能量泄漏检测需要掌握芯片使用的算法和实现方式。为避免这些前提条件，本文提出一种基于协方差矩阵变异系数的能量泄漏评估模型。该模型在评估能量迹的能量泄漏情况时无需对芯片实施具体的侧信道分析，也不需要使用芯片所用算法和实现方式，大幅降低了芯片设计者、攻击者和测评者对侧信道分析方法的使用要求，可以在芯片设计完成时、侧信道攻击前和安全测评初期对芯片安全性进行准确评估。下一步将利用本文模型对现有密码芯片进行评估分析，研究评判实际产品能否通过侧信道安全性评估的标准。