5G 超密集异构网络带内无线回传资源分配方案

余钊贤，易辉跃，裴 俊

（1.中国科学院上海微系统与信息技术研究所中科院无线传感网与通信重点实验室，上海 200050；2.中国科学院大学，北京 100049；3.上海无线通信研究中心，上海 201210）

0 概述

在5G 时代背景下，智能物联网设备数量的指数级增长使人们对于数据日常业务的需求迅速增加，从而对无线蜂窝网络中的容量也提出了更高的要求［1］。对此，新一代无线通信系统中涌现出很多候选的解决方案［2-3］，如大规模MIMO 技术、超密集网络技术、毫米波通信技术、全双工技术等。大规模MIMO 技术在基站端安装大规模天线阵列，进而可以为大量用户提供服务，能够满足现有的用户需求并且具备更为突出的能量效率和频谱效率［4］。超密集网络技术［5］在小区内部署大量的小功率基站，同样可以满足小区的大规模业务需求，同时也提高了频谱效率以及服务质量。因此，结合上述两种技术优点的超密集异构网络［6］近年来受到了行业人士的广泛关注，并且将是5G 时代无线通信的关键技术之一。

超密集异构网络能够极大程度地提高系统容量，具有较高的频谱效率和服务质量，能够满足5G时代eMBB 和mMTC 两大典型场景的业务需求［6］，但同时也存在一些迫切需要解决的问题。超密集小区和大业务小区通过回传链路连接核心网，因而信道容量、延时性、能量效率以及部署成本都是必须要考虑的。超密集网络部署中若采用现有基于光纤链路的有线回传方案，需要将光纤连接到各个小基站，部署成本十分昂贵，显然不具备可行性，而低成本且便捷的无线回传方案可以很好地解决此类场景下的网络部署问题。此外，相较于目前低于6 GHz 的毫米波频段可用频谱资源少且波长较长的缺点，高于6 GHz 的毫米波频段有很多可利用的频谱资源，且毫米波通信的视距传播特性有利于系统的干扰控制，可用于5G 网络的基站带内无线回传。

文献［7-8］从频谱效率角度、文献［9-10］从能量效率角度、文献［11-12］从频谱效率和能量效率结合的角度分别对5G 超密集异构网络的无线回传方案进行了研究，但仍不能很好地满足5G 网络对于回传的要求，小区间干扰、回传链路的动态变化和用户调度等问题未得到有效解决。小基站的回传问题仍然制约着5G 网络部署的发展。

本文研究双层异构网络模型，在队列稳定和无线回传资源有限的情况下，综合考虑超密集小区和大业务小区内的用户调度、功率分配、干扰控制和动态变化等因素，对带内无线回传的最优资源分配问题进行数学建模并求解，提出基于李雅普诺夫优化理论［13］的联合用户调度和功率分配的优化算法。利用复杂度较低的MOSEK 求解器得到调度向量的连续解，并通过二分类算法将求得的连续解恢复为具有0-1 限制的调度向量。在此基础上，采用拉格朗日乘子法分别对宏基站和小基站的功率分配问题进行求解，通过队列的时间迭代更新给出最优资源分配方案。

1 系统模型

1.1 网络模型

本文研究5G 超密集异构场景下带内无线回传链路与接入链路的资源分配问题，使用的双层异构网络系统模型如图1 所示。其中，以宏基站（MBS）为中心的矩形区域内均匀部署S个全双工小基站（FD-SC），宏基站通过回传链路向小基站传输数据，各基站通过接入链路服务其小区内的用户。宏基站包含数量为N的天线，并且服务M个单天线的宏用户和S个小基站，宏基站直接调度的用户总数K=M+S，天线数量N=2K。

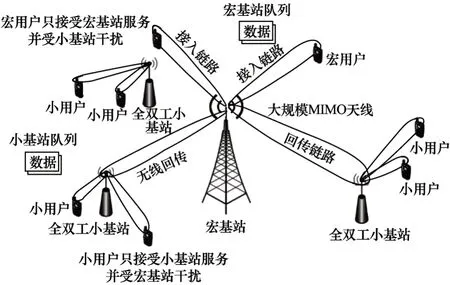
图1 双层超密集异构网络系统模型Fig.1 System model of two-tier ultra-dense heterogeneous network

每个小基站服务其小区内的Ns个小用户，各基站的天线数为Nt=Ns+1，小基站用户总数可表示为L=S×Ns，因此，整个系统中的用户总数Ks=M+S×Ns，其中，s表示第s个小基站（s=0，1，…，S）。分别以各个小基站作为中心对区域进行划分，即得到S个小小区，每个小基站的1 根天线用于与宏基站之间的无线回传，另外Ns根天线用于服务其小小区内的单天线小用户（SUE），并假设不考虑小基站自身引起的自干扰。在该模型中，以共信道时分双工（Co-channel TDD）作为通信协议，宏基站与小基站共享整个通信带宽，可以同时进行下行链路的数据传输，且Ks，K，M，N，S，L，Ns＞＞1。

1.2 信道模型

信道模型描述以宏基站和宏用户为例。宏基站与所有M个宏用户之间的信道矩阵可由式（1）表示：

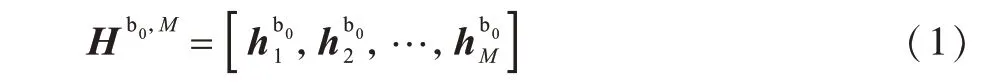
用户终端的移动性所带来的误差使得信道状态信息出现偏差，式（1）中信道矩阵Hb0，M的估计值表示为：

第m个宏用户与宏基站之间的信道矩阵即非理想信道状态信息，可由式（3）建模［14］：

考虑路径损耗和阴影衰落引起的大尺度衰落，且用户随机分布在基站周围，具有不同的信道增益，信道相关矩阵可以建模为。其中：增益与基站和用户之间的距离、通信频段、基站天线增益有关为小尺度衰落的信道矩阵估计值，分别为实际信道和噪声，可以建模为均值为零、方差为1/N的高斯随机矩阵；τm为宏基站与第m个宏用户之间的信道估计误差，当信道状态处于理想状态时，τm=0。

2 优化问题建模

2.1 调度向量和功率向量

宏基站的下行链路通过接入链路为宏用户提供数据传输，通过回传链路为小基站提供数据传输，小基站则通过接入链路服务其小区内的小用户。分别定义宏基站调度向量和小基站调度向量来表示当前t时刻接受服务的用户集：

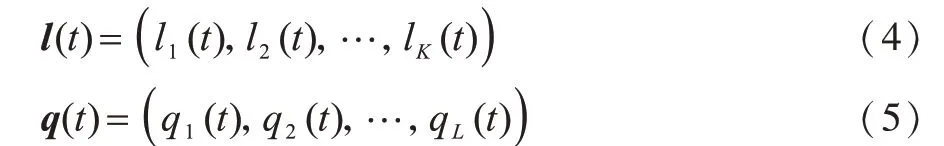
其中，lk(t)=1 或qi(t)=1 表示用户在t时刻接受服务，lk(t)=0 或qi(t)=0 表示用户在t时刻不接受服务。

2.2 预编码器设计

理论上，工作在全双工模式下的基站通信可以达到两倍的信道容量，能够减小反馈延迟以及端对端的传输时延，但同时也会带来干扰。干扰可以分为跨层干扰和同层干扰，其中，跨层干扰指相邻宏用户或者其他小基站所带来的干扰，同层干扰指相同小区的其他小用户或者其他小区内的小用户带来的干扰［16-17］。在宏基站端设计预编码器［18］可以将干扰信道转化为MISO 信道来控制全双工带来的干扰，从而将接收机中总的全双工干扰处理为噪声。宏基站的天线一部分被用来服务其宏用户以及小基站，另一部分则被用来消除其对小用户的干扰。宏基站端的预编码器设计如式（6）所示：

其中，U和T分别用于控制跨层干扰和同层干扰。本文考虑信道慢变的情况，根据式（3）的信道估计值计算基站与小用户之间信道的相关矩阵，然后在相关矩阵的零空间中进行传输，从而消除宏基站与小用户之间的干扰。因此，预编码器U可由式（7）表示：

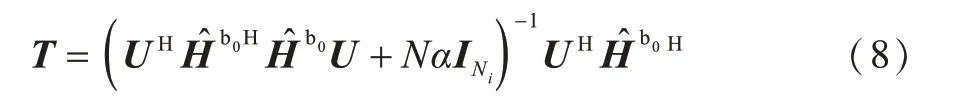
其中，参数α为正则化系数。

假设全双工干噪比门限为ε0，由式（9）定义从第s个小基站到任一接受调度的接收用户i的全双工干扰噪声比，即干噪比：

其中，ηi为接受者i处的热噪声。

工作在全双工模式下的基站会带来全双工干扰，从而影响基站用户之间的通信。因此，需要对全双工干扰进行限制，即应使全双工干噪比满足式（10）所示的约束条件：

类似地，小基站下行传输时小用户也会受到来自同小区其他用户所带来的同层干扰。因此，在小基站端也需要采取类似的预编码方案。

2.3 下行传输信号模型

结合用户调度向量、功率向量、信道以及预编码器表示t时刻下宏用户、小基站和小用户处的接收信号。由于基站工作在全双工模式，因此会对各接收信号带来跨层干扰及同层干扰，同时为了表示方便，本文不考虑时间依赖性。

t时刻第m个宏用户处的接收信号如式（11）所示，t时刻第s个小基站处的接收信号和第s个小基站下第i个小用户cs，i处的接收信号分别如式（12）和式（13）所示：

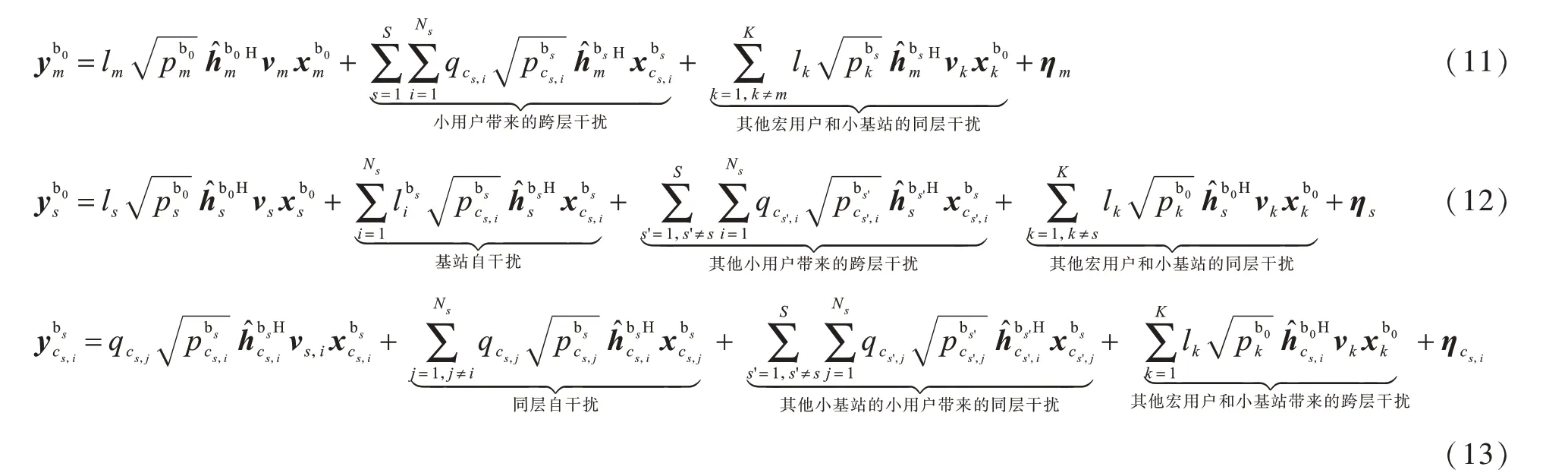
根据式（11）～式（13）可得宏用户、小基站和小用户处的信干噪比，分别如式（14）～式（16）所示：

对于给定的调度向量l、q，以及干扰抑制矩阵U和发射功率分配向量p，定义一个组合控制变量Λ={l，q，U，p}，显然，Λ与空间信道相关矩阵有关。对于给定的组合控制变量Λ，宏用户、小基站和小用户处的遍历数据速率分别如式（17）～式（19）所示：

综上所述，平均数据速率区域即用户平均数据速率的凸包，可由式（20）表示：

总功率约束且无自干扰条件下的速率域边界点是帕累托最优的［19］。如果干噪比协方差矩阵接近恒等矩阵，则该系统的帕累托速率域是凸的［20］。因此，在上述约束条件下，该速率域是帕累托最优的且满足凸条件。

2.4 下行最优资源分配问题的数学建模

上述通信网络在离散时间t∈{0，1，…}内可以建模为排队网络模型。假设第i个用户的泊松到达数据为ai(t)，到达数据流之间独立同分布并且都满足泊松分布，则宏基站处的数据队列可定义为：

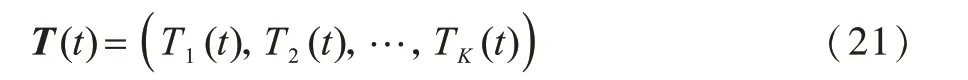
为便于优化问题求解，本文对宏基站数据队列T(t)进行扩展，引入宏基站虚拟队列对应小基站的无线回传队列：

其中，前M项与T(t)的前M项对应，后L项与无线回传队列对应。

宏基站端发送队列缓存的时间更新过程如式（23）所示：

t时刻小基站的无线回传队列如式（24）所示：

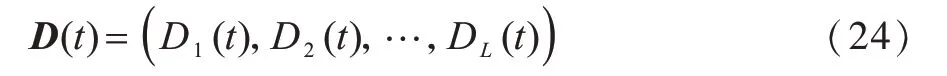
小基站端无线回传队列缓存的时间更新过程如式（25）所示：

定义第k个用户的突发到达数据的上界为0 ＜

在给定空间信道相关矩阵Θ的条件下，可用f（·）来定义凸包R内的网络效用函数，此时带内无线回传的资源最优分配问题的目标即在非理想信道状态信息和无线回传队列有限的条件下最大化网络效用函数。因此，资源最优分配问题可以建模为：

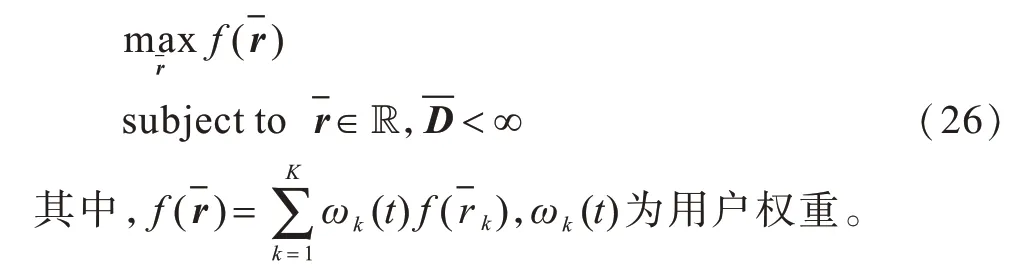
为解决上述复杂的优化问题，根据随机矩阵理论对数据速率以及平均发射功率进行处理，从而得到确定性等价形式的闭式表达式［20］。式（14）～式（16）的确定性等价形式如式（27）～式（29）所示：

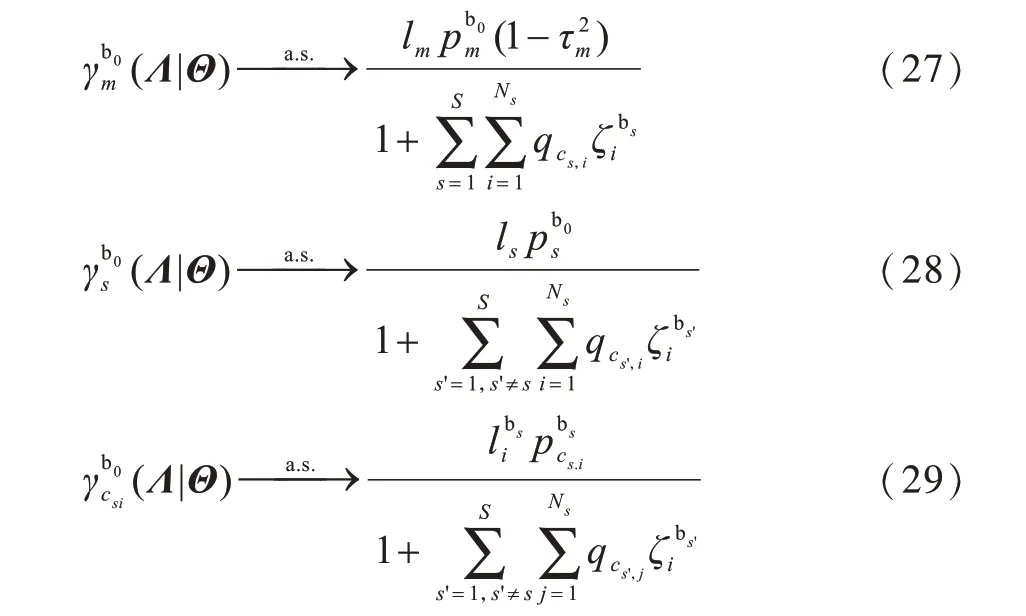
进一步地，通过引入辅助变量φ(t)=(φ1(t)，φ2(t)，…，φk(t))来代替优化问题约束条件，该辅助变量满足：

此时，无线回传队列的更新过程可以表示为：

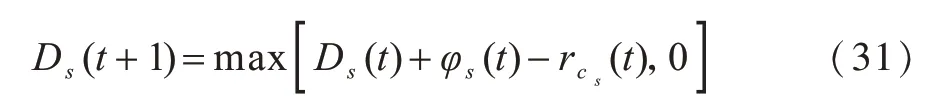
因此，网络稳定性约束下式（26）所示的优化问题可以表示为：

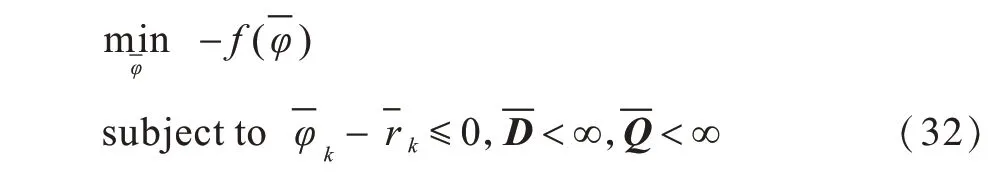
此时，系统队列缓存向量可以表示为Σ(t)=[Q(t)，Y(t)，D(t)]。

3 基于李雅普诺夫优化算法的优化问题求解

3.1 李雅普诺夫优化算法

结合2.4 节的分析，对于给定的组合控制变量Λ，最优资源分配问题即为在凸区域上联合复合控制变量和动态网络传输负载变化的时间平均优化问题，目标是在队列稳定条件下最大化网络效用函数。式（32）所示的优化问题可通过李雅普诺夫优化算法来求解［13］。

根据t时刻的队列缓存向量，t时刻的李雅普诺夫算法函数可由式（34）表示：

此时，李雅普诺夫漂移如式（35）所示：

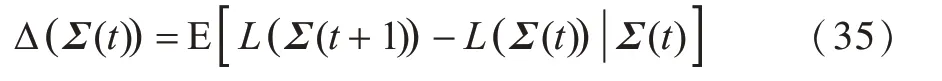
根据基本不等式max[a，0]2≤a2和(a±b)2≤a2±2ab+b2，不考虑时间依赖性可得：

由于数据到达速率、数据传输速率和辅助变量具有上界，因此整理上述结论可得：

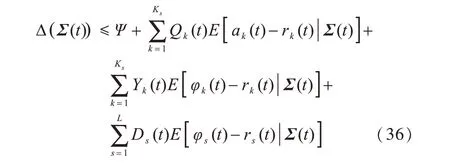
为便于表示，用Π表示式（36）等号右边部分，即Δ(Σ(t)) ≤Π。Ψ为满足下式的有限常数：

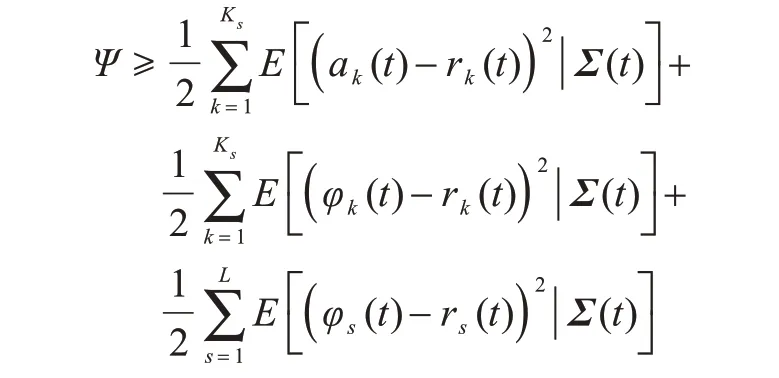
此时，根据李雅普诺夫漂移加惩罚算法，式（32）所示的优化问题可转化为最小化李雅普诺夫漂移，即：

其中，v为非负的李雅普诺夫优化参数。由于Ψ是有限常数，因此根据推导得出的式（36），式（37）所示优化问题的求解即最小化式（38）。式（38）可分解为调度向量求解（1△）、辅助变量求解（2△）以及宏基站和小基站的功率分配求解（3△、4△）4 个部分。在同一时刻，分别最小化上述4 个部分的解，即可求得当前时刻的最优调度向量、辅助变量和功率分配向量。

结合系统队列和预编码器设计并且通过整理式（38）中的子问题，得到联合用户调度和功率分配的算法框架，如图2 所示。

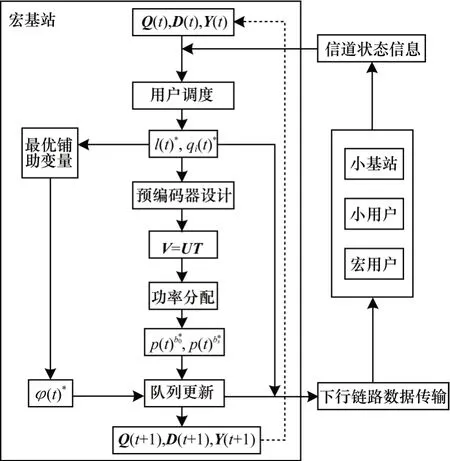
图2 联合用户调度和功率分配的优化算法框架Fig.2 Framework of optimization algorithm combining user scheduling and power allocation

3.2 用户调度向量求解

调度向量的优化问题1△是含有混合整数变量的非凸优化问题。首先将调度向量的整数约束lk(t)，qcs，i(t)∈{ 0，1}松弛到具有连续值的线形约束，即lk(t)，qcs，i(t)∈[0，1]；然后根据全双工干噪比约束式（10），以最大界限1+ε0替换目标函数中的分母，从而将求解优化问题转化为最小化其上界的问题，即求解式（39）所示的优化问题。为描述方便，令Ak(t)=Qk(t)+Yk(t)。

为确保所有用户都能接受服务，在调度问题的优化求解中，假设每个用户具有相同的基站发射功率，确保得到最优调度向量。在每个时刻t，利用复杂度更低的MOSEK 求解器求解问题式（39）来得到调度向量的近似最优解。根据仿真结果，调度向量的近似最优解接近于二元分布。

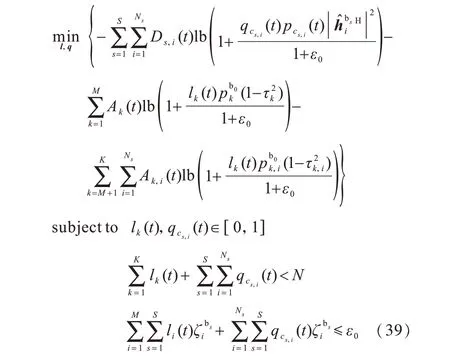
为获得更精确的调度向量的整数解，本文利用复杂度较低的二分类算法将连续松弛解转化为整数解。首先根据设置的阈值ζ将用户集分为U1=和U0=≤ζ，然后根据目标函数中不确定用户集的最大权值进行降序排列，依次检验用户是否满足约束条件，若满足，将该不确定用户归入用户集U1；若不满足，则归入用户集Uo，直到对所有不确定用户进行归类或者超出上述两个约束条件，二分过程结束，保留用户集U1为当前时刻的调度用户，舍去用户集Ux和Uo即可得到最优调度向量。

3.3 辅助变量求解

对于最优辅助变量2△的求解，即求解式（40）所示的优化问题：

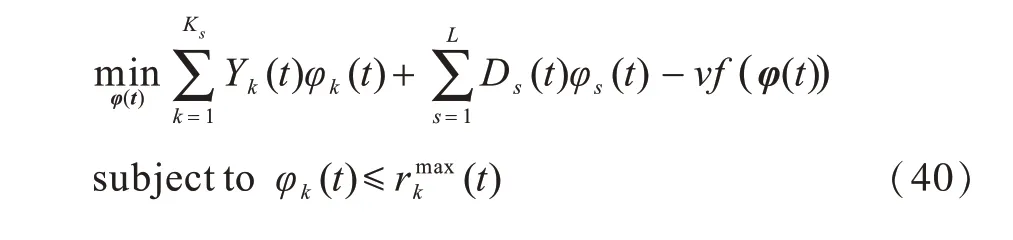
由于上述问题是严格凸的，因此通过一阶微分即可解得：

3.4 功率分配

在解得最优调度向量的基础上，结合式（7）可解得预编码器U，此时需要对接受服务的用户进行功率分配。

3.4.1 宏基站功率分配

宏基站的功率分配可通过求解3△得到，如式（42）所示的优化问题：

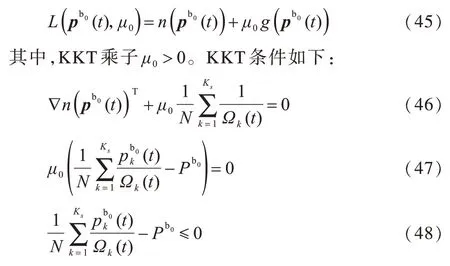
3.4.2 小基站功率分配

与宏基站功率分配类似，对于第s个小基站的功率分配，可以由式（52）所示的优化问题得到其功率分配情况。

由于目标函数在pcs，i(t)≥0 情况下是严格凸的，约束条件是紧的，因此存在最优解。此处可用拉格朗日乘子法来求解上述优化问题。拉格朗日函数可写为：

根据每个时刻t的最优调度向量以及功率分配向量，由式（23）、式（25）和式（33）对队列进行更新，并重复上述步骤。

4 仿真结果及分析

4.1 复杂度分析

在多用户场景下，本文提出的优化算法主要分为预编码器设计、优化问题求解和队列更新3 个部分。

2）优化问题求解的复杂度为5L4+5KL3+(2S+7)K+(2S+8)L+3S+M+O((M+S+L)3.5W2)+(2S+2)O(L3)，其中，L×L矩阵求逆的复杂度为O(L3)。MOSEK 求解器使用内点法解决优化问题，复杂度为O(n3.5W2)，其中，n为变量维数，W为求解器内置参数。

3）队列更新复杂度为2L2+11L+9M+6S。

由上述分析可以看出：在单用户场景下，本文算法复杂度随着基站数和用户数增多而增加；在多用户场景下，多个小小区用户会导致算法各部分复杂度增加，各个小基站需要做用户调度和功率分配，这会在一定程度上增加算法复杂度。

4.2 仿真结果

分别在28 GHz、10 GHz 和2.4 GHz 频段下对本文系统模型进行仿真实验，并对单用户场景（Ns=1）和多用户场景（Ns=4）的仿真结果进行比较。将信道模型建模为3 个频段下城市环境中以距离为基础的视距路径损耗模型，具体参数如表1 所示［21］。此外，到达数据在28 GHz、10 GHz 和2.4 GHz 频段下分别服从均值为1 Gb/s、100 Mb/s 和20 Mb/s 的泊松分布，网络效用函数选用速率的对数函数，即f()=lb。仿真参数设置如表2 所示。

表1 视距路径损耗模型参数Table 1 Parameters of LOS path loss models

表2 仿真参数设置Table 2 Parameters setting of simulation

图3～图5 分别体现了28 GHz、10 GHz 和2.4 GHz 3 个频段下用户总吞吐量、边缘用户总吞吐量和网络效用函数值相对小区密集程度的关系。其中：小基站数量从16 增加到100，与此对应，基站之间的距离从250 m 缩短到100 m；在多用户场景下，宏小区即每平方千米的用户总数从80 增加到500，与此对应，单用户场景下宏小区用户密度从32 增加到200。

仿真结果表明：在同一频段、基站数相同的情况下，由于用户数量的大幅增加，基站服务多用户场景的总用户吞吐量约为单用户场景的2 倍，平均用户吞吐量略低于单用户场景，整体网络效用得到了有效提升；在2.4 GHz、10 GHz 和28 GHz 这3 个频段下，根据本文给出的带内无线回传方案，基站数的增加会导致平均用户吞吐量和平均边缘用户吞吐量逐渐下降，但整体网络效用函数值逐渐增加，达到网络队列稳定前提下最大化网络效用的目标，且单用户场景下的性能明显优于多用户场景；在多用户场景下，由于28 GHz 频段带宽为2.4 GHz 频段带宽的50 倍，因此平均用户吞吐量大幅提升。由此可以看出：当基站间距离为250 m 时，28 GHz 频段通信的平均用户吞吐量约为2.4 GHz 频段通信的79 倍；当基站间距离为100 m 时，28 GHz 频段通信的平均用户吞吐量约为2.4 GHz 频段通信的47 倍。

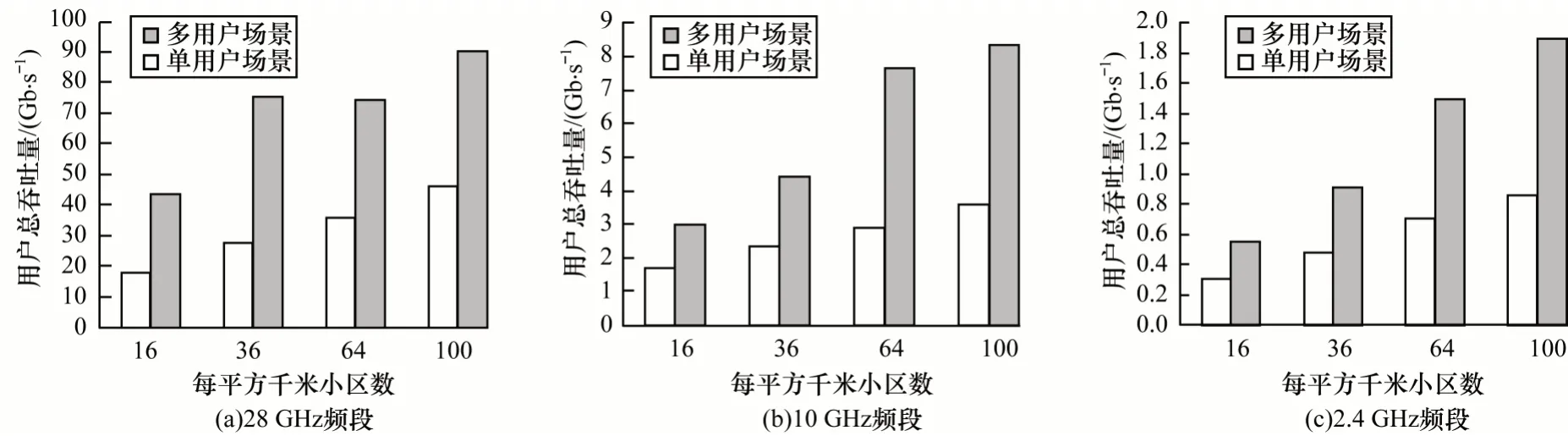
图3 28 GHz、10 GHz 和2.4 GHz 频段下用户总吞吐量与小区密度的关系Fig.3 Total user throughput versus number of small cells at 28 GHz，10 GHz and 2.4 GHz bands

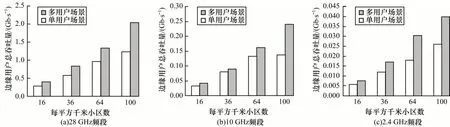
图4 28 GHz、10 GHz 和2.4 GHz 频段下边缘用户总吞吐量与小区密度的关系Fig.4 Total cell-edge user throughput versus number of small cells at 28 GHz，10 GHz and 2.4 GHz bands

图5 28 GHz、10 GHz 和2.4 GHz 频段下网络效用与小区密度的关系Fig.5 Network utility versus cell density at 28 GHz，10 GHz and 2.4 GHz bands

5 结束语

本文研究多用户场景下5G 超密集异构网络的带内无线回传方案，提出基于李雅普诺夫优化的用户调度和功率分配算法，并利用MOSEK 求解器和二分类算法获得精确的用户调度向量，在无线回传资源有限、信道状态信息不理想的情况下给出合理的带内无线回传方案。仿真结果表明，在多用户场景下，本文方案的用户总吞吐量、边缘用户总吞吐量和网络效用性能优于单用户场景，并且利用毫米波频段进行通信可以得到优于传统蜂窝网络频段的平均用户吞吐量。在本文考虑的系统模型中，用户以就近原则接入基站，下一步将从用户随机接入的角度出发，通过引入非高斯信道模型和基站自干扰消除技术对本文方案做进一步优化。