基于SVD 和ARIMA 的时空序列分解与预测

杨立宁，李艳婷

（上海交通大学机械与动力工程学院，上海 200240）

0 概述

时空数据是指同时具有时间和空间维度的数据［1］，传感器、移动电话、射频识别（RFID）和智能电网等智能设备的发展促进了实时时空数据流的采集。考虑一个时空随机过程，时空建模的目标是基于时空数据构建时空模型以对给定时刻所有位置的行为进行预测［2］。若不考虑时间因素，可以采用单纯的空间模型进行建模，如kriging 方法［3］，但是其准确性较低，添加时间维度可以提高预测的准确性。随着时空数据流采集难度的降低，时空序列建模逐渐成为学者们的研究热点之一。

目前，关于时空序列预测主要分为基于物理模型、基于统计模型和基于机器学习的3 种方法。基于物理模型的方法首先对时空序列的机理进行研究，寻找其内在的系统动力学规律并构建系统动力学模型，然后对时空序列进行表达进而预测。其中，JONES 等人［4］提出随机偏微分方程以描述连续型时空随机过程。基于统计模型的方法主要分为描述型时空模型和动态时空模型两类。前者利用统计学中的描述型统计量表达时空模型的性质，并对统计量进行建模以消除随机误差；后者考虑时间和空间的自相关性并利用过去和其他地区的数据对当前数据进行建模，然后实现迭代更新预测。近年来，随着机器学习和深度学习的不断发展，人工智能技术被广泛应用于时空序列建模和预测任务。通过机器学习模型能够提取时空序列中复杂的特征模式，也可以对高维时空序列进行降维和聚类从而使得分析更简便。

本文提出一种分离时空数据中的时间模式和空间模式并分别建模的方法。对原始数据进行平稳性检验并中心化，利用奇异值分解（SVD）分解中心化的数据集，通过时间序列模型中经典的ARIMA 模型对时间模式建模并检验其有效性，然后利用ARIMA 模型预测时间序列，将预测结果与空间模式相结合并对真实时空序列进行重建，以得到各个地理观测点的预测值。

1 相关工作

描述型时空模型较早以时空协方差为研究对象，通过对样本协方差值进行曲面拟合获得协方差函数，然后利用协方差函数分析时空模式的演变。时空kriging 方法［5-7］基于时空过程的协方差函数给出未知地区给定时刻的最优线性无偏估计。但是，由于时空协方差是一种描述型统计量，很难解释时空模式的内在动态变化。描述型时空模型在数学上更通用，但是动态时空模型在科学上有更强的解释性［8］。动态时空模型基于条件概率分布进行建模，其中最主要的动态时空模型为层次时空模型。层次时空模型可分为2 个主要类别：一类是经验层次模型，其认为观测到的时空过程是真实时空过程的演变以及真实过程通过某种函数作用产生观测过程，其机制类似于隐马尔可夫过程；另一类是贝叶斯层次模型，和经验层次模型的主要区别在于，贝叶斯层次模型认为真实过程中的参数也是动态变化的，其在经验层次模型的基础上增加了底层的参数过程，因此，贝叶斯层次时空模型将时空序列过程分解为参数过程、真实过程和数据过程3 个层次并分别建模［8-10］。

无论经验层次模型还是贝叶斯层次模型，真实过程都是最重要的，其对理解时空动态变化模式具有重要意义。因此，时空模型的一个研究重点在于真实过程的模型构建。统计时空模型的构建主要来源于时间模型和空间模型的结合。CLIFF 和ORD 较早将时间序列模型应用于空间分析中，提出空间自回归模型（SAR）、空间移动平均模型（SMA）和空间回归模型（SR）等［11］。MARTIN 和OEPPEN 将空间信息整合到传统的ARIMA 模型［12］中，提出STARMA模型［12］。STARMA 定义了空间阶次的概念并在真实应用中产生了良好效果［13-15］。但是，随着时空数据的概念外延，STARMA 模型中关于欧式距离越小则空间阶次越低的假设越来越难以满足，使得其在一些未知空间相关性结构的数据集中表现较差。BESSA等人结合其他地区的历史数据和待预测地区的数据，构建向量自回归模型VAR［16］以对时空序列进行建模描述。但是，VAR 模型中的待估计参数空间较大，一方面需要消耗极大的计算资源，另一方面可能由于样本量不足而引起过拟合问题。因此，基于Lasso 的VAR（Lasso-VAR）模型被广泛应用［17］，尽管Lasso-VAR 在一定程度上解决了模型过拟合问题，但是其优化模型变得更难求解，计算成本过高。

BAHADORI 等人［18］通过将时空数据作为张量进行处理，提出一种低秩张量学习框架以进行多元时空序列分析。BAROCIO 等人［19］通过动态模式分解的方式对时空数据进行降维并提取时空特征。LI［20］利用梯度提升回归树（Gradient Boosting Regression Tree，GBRT）算法对城市共享单车的时空数据进行建模并预测数量。在深度学习方法中，递归神经网络（Recurrent Neutral Network，RNN）和深度神经网络（Deep Neutral Network，DNN）被广泛应用于时空序列模型构建任务。SHI［21］利用RNN 模型的一个变体，即长短时记忆（Long and Short Term Memory，LSTM）网络对地区的降雨量进行预测。CHE 等人［22］将传统的RNN 拓展到时空领域，提出时空递归神经网络（Spatio-Temporal Recurrent Neural Network，ST-RNN），以对时空序列进行建模预测。类似地，在深度学习方面，ZHANG 等人［23］将深度残差网络拓展到时空领域，提出时空深度残差模型（ST-ResNet）以对人流量进行预测。

2 算法描述

2.1 时空数据的奇异值分解

SVD 是一种矩阵分解技术，其在信号处理和统计学中有很多应用［24］。给定一个秩为l的时空数据矩阵YD×T，其中，D表示空间中观测点的个数，T表示采样时间点的个数。时空数据矩阵YD×T的奇异值分解如下：

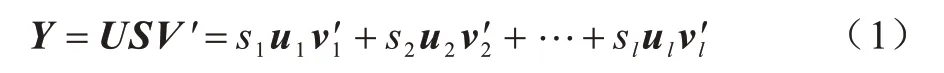
其中，U=(u1，u2，…，ul)，V=(v1，v2，…，vl)，S=diag{s1，s2，…，sl}，且s1≥s2≥…≥sl≻0。向量是左奇异矩阵的列向量，向量vi′（i=1，2，…，l）是右奇异矩阵的行向量，标量si称为奇异值。

假设{cm：m=1，2，…，T}是矩阵YD×T的列向量，cm代表给定的m时刻D中所有空间单元的观测值，YY′表达了D空间单元之间的相关性，这里假定YD×T已经去中心化为零均值矩阵。矩阵YD×T的ui事实上是相关矩阵YY′的特征向量，u1表示相关矩阵YY′对应特征值最大的特征向量，包含了空间相关性最多的信息量，或被称为“空间模态”，表征了空间相关性的模式。ui的第j个分量uij表示第j地区对第i空间模态的“贡献”。类似地，假定{r′n：n=1，2，…，D} 是矩阵YD×T的行向量，r′n代表n位置在整个时间段的观测值向量，Y′Y表达了不同时刻之间的相关性，矩阵YD×T的vi′事实上是相关矩阵Y′Y的特征向量，r1表示相关矩阵Y′Y对应特征值最大的特征向量，包含了时间相关性最多的信息量，或被称为“时间模态”，表征了时间相关性的模式。r′i的第j个分量r′ij表示第j时刻对第i时间模态的“贡献”。时空矩阵YD×T分解后的S是奇异值矩阵，si表示模式i的重要程度，例如，若s1是最大的奇异值，则s1对应的模式1 具有表征空间模式的最重要的特征。

2.2 基于SVD 的时空序列模型

给定历史时空数据矩阵YD×(t-1)，对当前时刻t的各个地理观测点进行预测的具体步骤如下：

步骤1通过SVD 对中心化后的时空矩阵进行分解。

假定历史时空数据矩阵YD×(t-1)的秩为l，可利用式（1）得到如下分解：

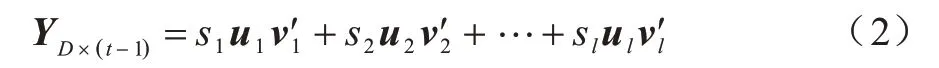
SVD 有一个重要的性质，定义奇异值占比Er=，则当r＜＜l时，Er可达到85%以上的水平，剩余的可认为是噪声。因此，通过选取前几个奇异值与对应的左奇异向量和右奇异向量进行重建，可以对矩阵实现降噪，如下：

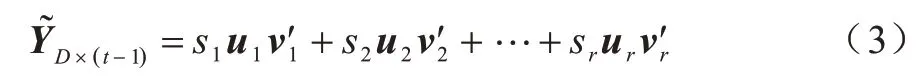
步骤2通过ARIMA［25］对时间模式进行建模预测。

由于分解之后得到的右奇异向量vi′可以看作时间序列，因此本文利用时间序列中应用最广泛、效果最好的ARIMA 模型进行建模。ARIMA 的标准模型如下：

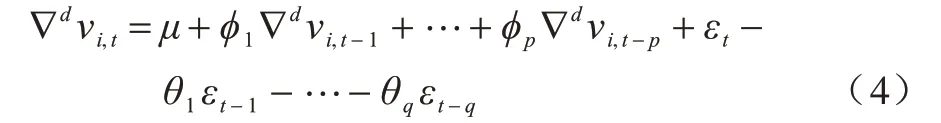
其中，∇dvi，t代表t时刻第i个向量的d阶差分，εt是t时刻均值为0 的随机误差，μ、φi（i=1，2，…，p）、θi（i=1，2，…，q）为待估计参数。利用AIC、BIC 信息准则和最大似然法进行模型选择和估计，当得到估计好的模型后，利用该模型进行h步向前预测，如下：

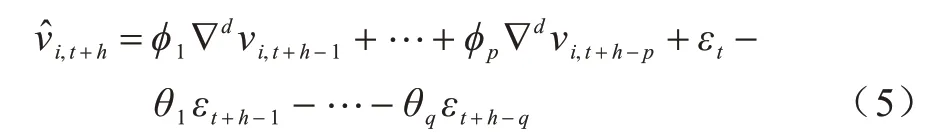
步骤3利用SVD 进行重建得到h步向前预测结果。

当得到时间模式的估计值后，利用已经存储的奇异值和对应的左奇异向量重建时空矩阵，得到最终预测结果：

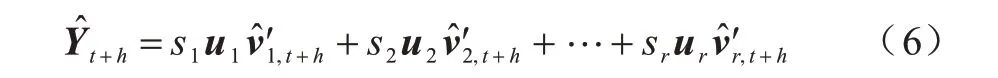
2.3 模型优化

模型优化包括奇异值选择和ARIMA 模型参数选择过程。针对奇异值选择，不同的奇异值个数重建的矩阵精度不同，通常情况下，利用前几个较大奇异值即可基本重构原始时空矩阵，剩余奇异值可理解为由数据波动形成的噪音。本文通过遍历的方式验证了不同的奇异值个数对最后效果的影响，最终设定对前2 个奇异值对应的时间模式进行建模。针对时间模式ARIMA 模型的构建，首先需要对时间模式的平稳性进行检验，若不平稳，需要将其转化为平稳模式并在后续模型中逆推回真实预测结果；当数据平稳性检验通过后，利用ARIMA 模型对平稳时间模式进行建模，并利用ACF 和PACF 图［25］确定ARIMA 模型中的p、d和q参数取值；最后通过交叉验证以及信息准则AIC、BIC［26］对模型有效性进行检验并选择最优模型，在检验通过后，利用得到的ARIMA 模型完成预测。本文所提STSVD 算法描述如算法1 所示，算法流程如图1 所示。

算法1ST-SVD 算法

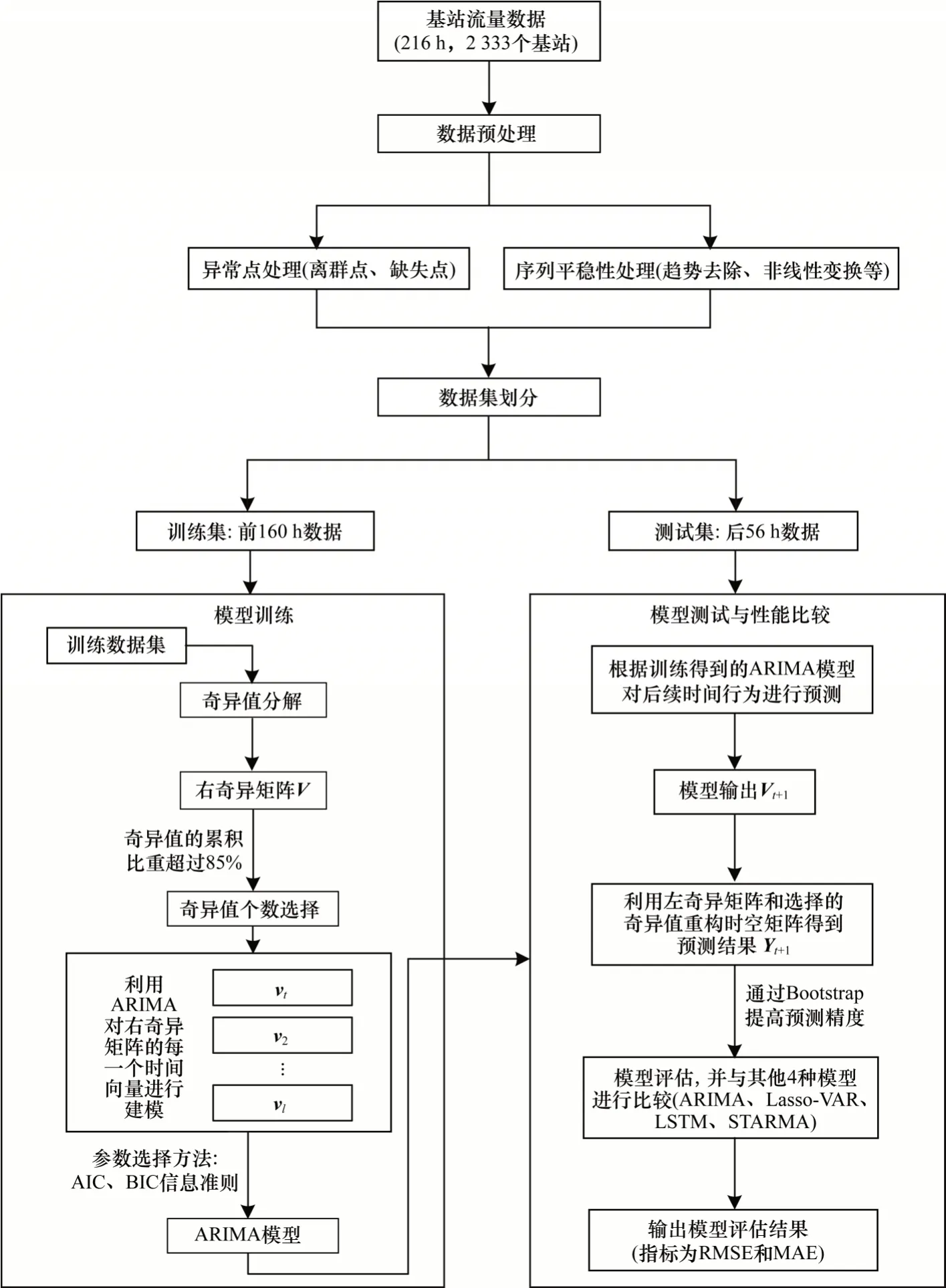
图1 ST-SVD 算法流程Fig.1 Procedure of the ST-SVD algorithm

3 案例分析

3.1 数据集描述

本文利用中国某大型城市的2 333 个基站在216 h（共9 天）内的流量数据对所提ST-SVD 算法进行验证，数据的采集频率为1 次/h。图2 所示为2 333 个基站的相对位置布局，经纬度已经过处理，表1 所示为其中5 个基站在13 h 内的流量数据示例。图3 所示为3 个基站在216 h 内的流量变化情况，从图3 可以看出，基站3 具有较明显的9 个峰，表明基站流量的变化基本以一天为周期，虽然另外2 个基站中基站1 也存在较类似的峰值，但是两者的整体变化有较大差异。本文将216 h 内的流量数据拆分成训练集和测试集，训练集包含前160 h 的数据，测试集包含剩余56 h 的数据。

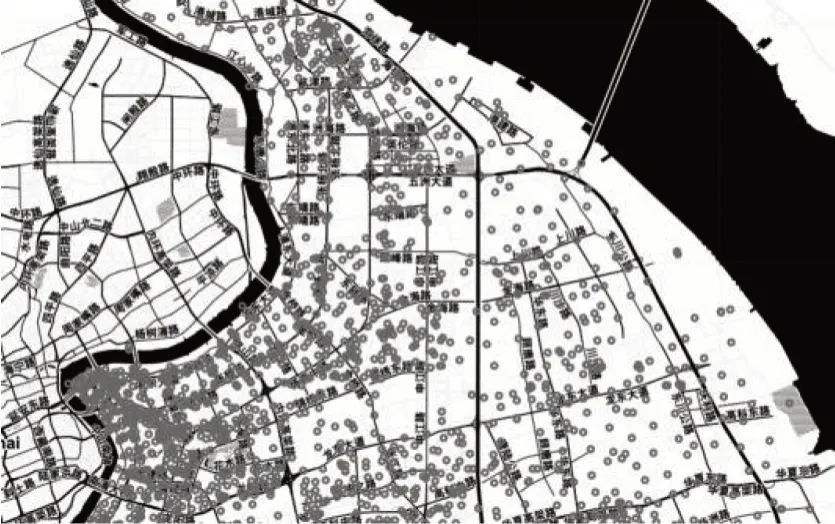
图2 2 333 个基站的布局Fig.2 Layout of 2 333 base stations

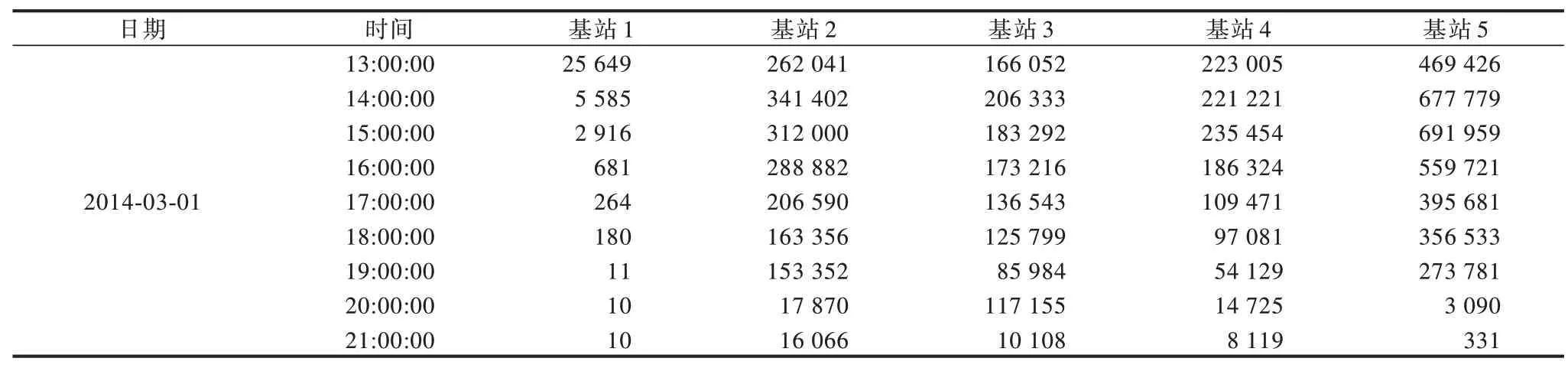
表1 5 个基站的部分历史流量数据片段Table 1 Partial historical traffic data fragments of five base stationsKb

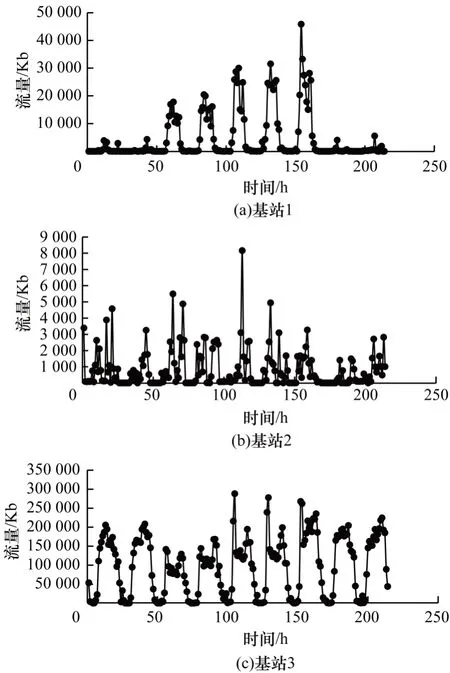
图3 3 个基站在9 天内的流量情况Fig.3 Traffic situation of three base stations in nine days

3.2 ST-SVD 模型构建

ST-SVD 模型构建步骤如下：

步骤1通过奇异值分解对中心化后的时空矩阵进行分解。在本案例中，时空矩阵Y的大小是2 333×160，在进行数据预处理（异常值处理、平稳性处理）之后，通过对处理后的Y进行奇异值分解，得到左奇异矩阵、右奇异矩阵和奇异值。图4 所示为截取的时空矩阵Y的右奇异矩阵，即时空序列的时间模式，此处截取了一天内每个小时之间的相关性情况，黄色区域表明相关性较强（彩色效果见《计算机工程》官网HTML 版），从图4 可以看出，时间相关性具有较明显的周期模式，并且可预测性较强。图5所示为时空矩阵Y中不同地点的皮尔逊相关系数与距离之间的关系，从图5 可以看出，针对该区域基站流量的时空数据，距离越近相关性越大的假设并不成立。

图4 时间相关性矩阵Fig.4 Time correlation matrix

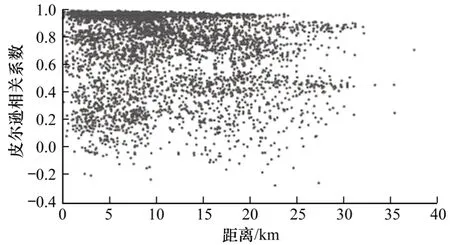
图5 相关性与空间距离的散点图Fig.5 Scatter plot of correlation and spatial distance

图6 所示为排序后的奇异值，一般而言，前几个奇异值即可涵盖大部分信息。从图6 可以看出，前2 个奇异值占据了奇异值之和的89%，因此，本文分别构建一个奇异值的重建算法ST-SVD（1）和两个奇异值的重建算法ST-SVD（2）。

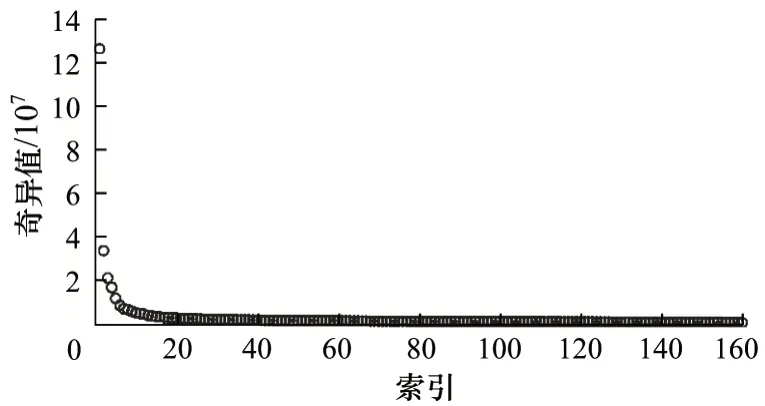
图6 降序排列的奇异值Fig.6 Singular values of descending order

图7、图8 分别对应前2 个奇异值的左奇异矩阵（空间模式）和右奇异矩阵（时间模式）。从中可以看出，空间模式较为复杂，没有明显规律，但是时间模式显示出明显的周期性和可预测性。因此，本文利用ARIMA 模型分别对2 个时间序列进行建模并预测。

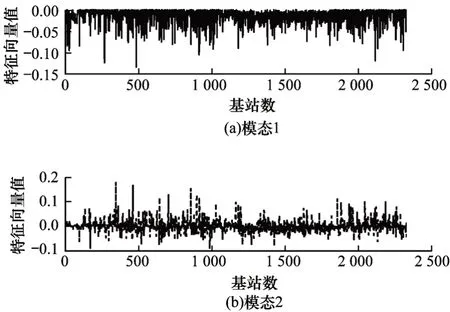
图7 左奇异矩阵Fig.7 Left singular matrix

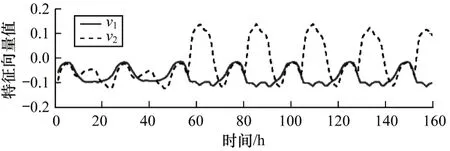
图8 右奇异矩阵Fig.8 Right singular matrix

步骤2通过AIC 和BIC 信息准则（表2）选择ARIMA 模型中的p、q、d参数并得到下述结果：

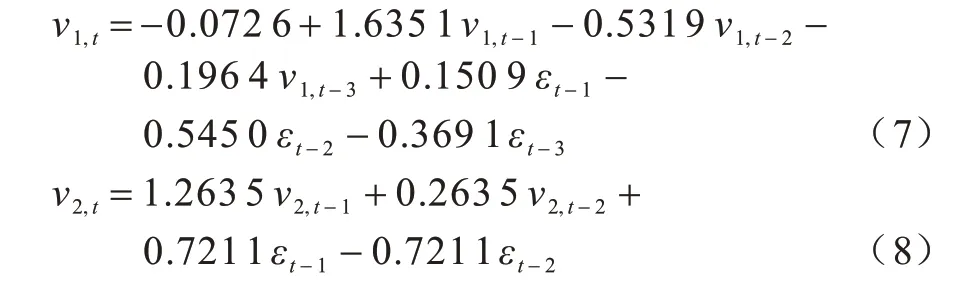
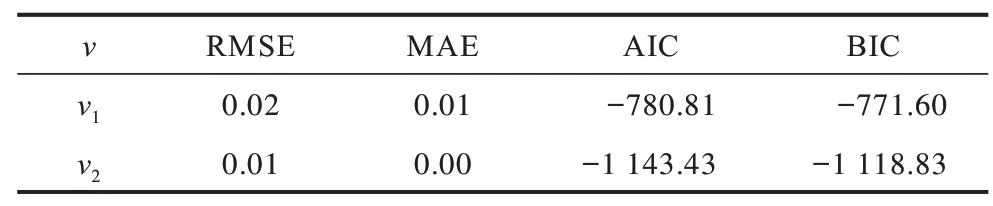
表2 模型拟合程度指标Table 2 Index of model fitting degree

RMSE 和MAE［27］的计算公式分别如下：

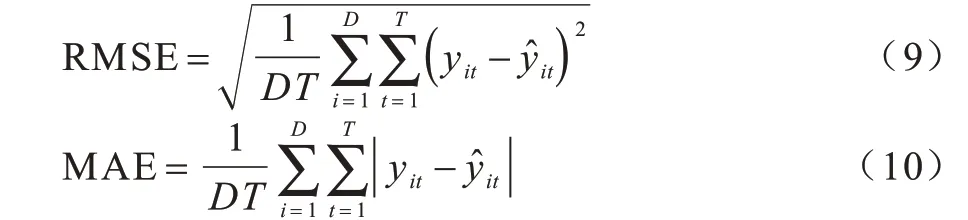
步骤3利用奇异值分解进行重建得到h步向前预测结果。在得到t时刻时间模式的预测值v1，t和v2，t后，即可利用式（1）结合左奇异矩阵和奇异值重建时空矩阵，得到t时刻空间各个位置的预测值。考虑到流量的周期性一般为一天，因此，本文利用ARIMA 模型分别向前1 步、向前6 步、向前12 步和向前24 步进行预测，并利用Bootstrap［28］从2 333 个基站中抽取不同的样本量，从100 次实验中取均值作为最终结果，以评估算法在整个周期内不同预测长度下的准确度和预测性能。

3.3 模型性能比较

本文将ST-SVD（1）、ST-SVD（2）与现有常用的ARIMA、Lasso-VAR、LSTM 和STARMA 4 种模型进行对比。其中，ARIMA 模型并不是时空序列模型，但是在不考虑空间观测点的相关性时时空序列变成独立的多个时间序列，可以分别利用ARIMA 进行建模预测。ARIMA 模型时间成本极高，但是可作为一种基线模型进行对比。Lasso-VAR 是带有Lasso 正则化约束的VAR 模型，其认为时空模型是时间序列模型加空间维度，即增加一维，然后通过传统的VAR模型并添加Lasso 正则化来降低过拟合风险。LSTM是递归神经网络的变体，适用于时间序列，其与VAR类似，将时空数据集的空间维度叠加到时间序列中进行训练预测。STARMA 模型是经典的时空分析模型，本文采用欧氏距离定义模型中的空间权重矩阵。实验过程中使用的软件、软件依赖包信息以及模型关键参数如表3 所示。

表3 实验过程中的软件、软件依赖包以及模型关键参数信息Table 3 The software，software dependency packages and key parameters information of the model during the experiment

利用10 个、20 个、50 个和100 个基站160 h 内的数据分别对上述6 种模型进行训练，并给出向前1 步、6 步、12 步和24 步的预测结果，利用常见的预测精度指标——均方根误差RMSE 和绝对值误差MAE 对预测性能进行评估。由于本文案例中共有2 333 个基站，为了提高性能评估的准确性并降低方差，通过Bootstrap 在2 333 个基站中随机选取上述10 个、20 个、50 个和100 个基站100 次，并对100 次的实验结果取平均值以作为最终的性能评估结果。

表4 所示为上述6 种模型向前1 步的部分预测结果，加粗数字为最优预测结果，括号中的百分数表示预测百分比误差，计算公式如式（11）所示表示预测值，y表示真实值。

从表4 可以看出：LSTM 模型的预测精度最差，原因是其数据量过少，模型欠拟合，这表明神经网络模型需要足够多的样本来提高精度；STARMA 模型优于不添加空间信息的ARIMA 模型；ST-SVD 的2 种模型相较于其他4 种模型预测准确率更优。具体地，利用2 个奇异值的ST-SVD（2）模型的预测误差约为0.13，ARIMA、Lasso-VAR、LSTM 和STARMA 的误差分别约为0.22、0.21、0.92 和0.19。ST-SVD（1）和ST-SVD（2）明显优于其他4 种对比模型且ST-SVD（2）优于STSVD（1）。

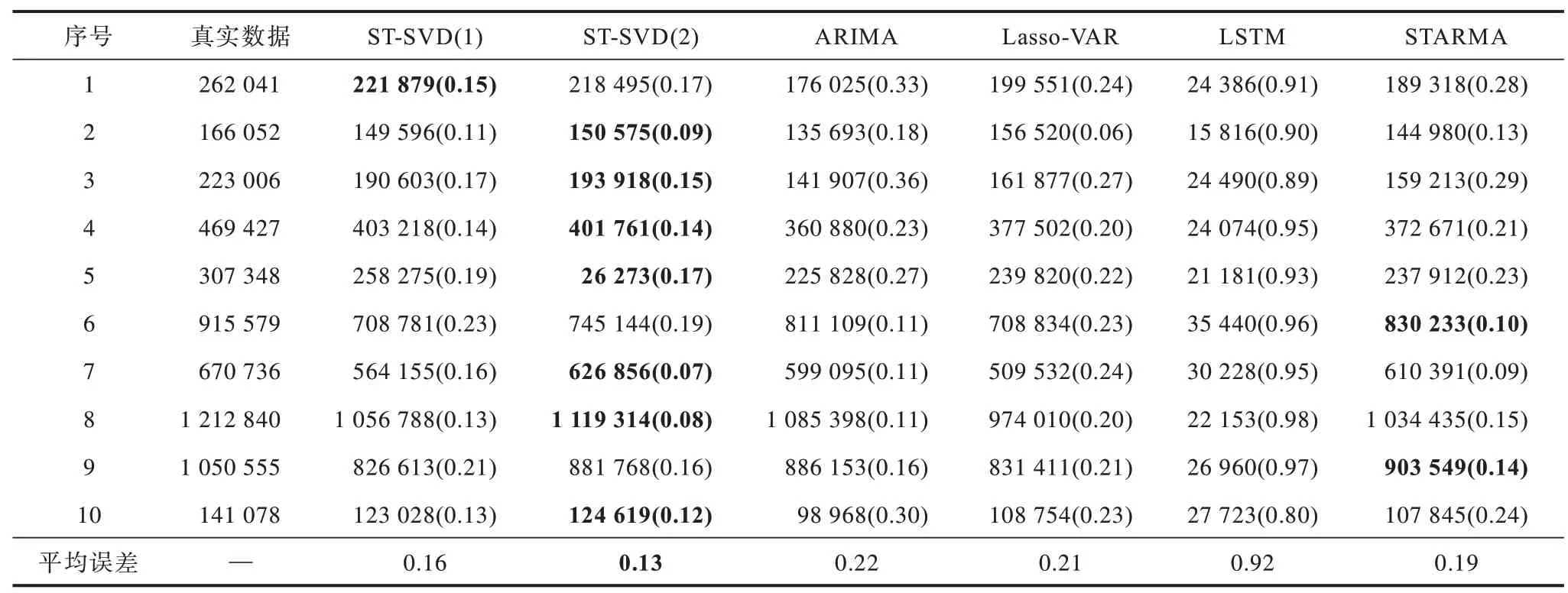
表4 6 种模型的1 步预测结果Table 4 One-step prediction results of six models

表5 所示为上述6 种模型在4 种不同基站个数以及4种不同预测步长情况下的RMSE，括号中为MAE。从表5可以看出，ST-SVD模型的性能明显优于其余4种对比模型，而且ST-SVD（2）的重构结果稍优于ST-SVD（1）的重构结果。从图9、图10可以直观地看出，2种ST-SVD模型的误差低于其余4 种对比模型。

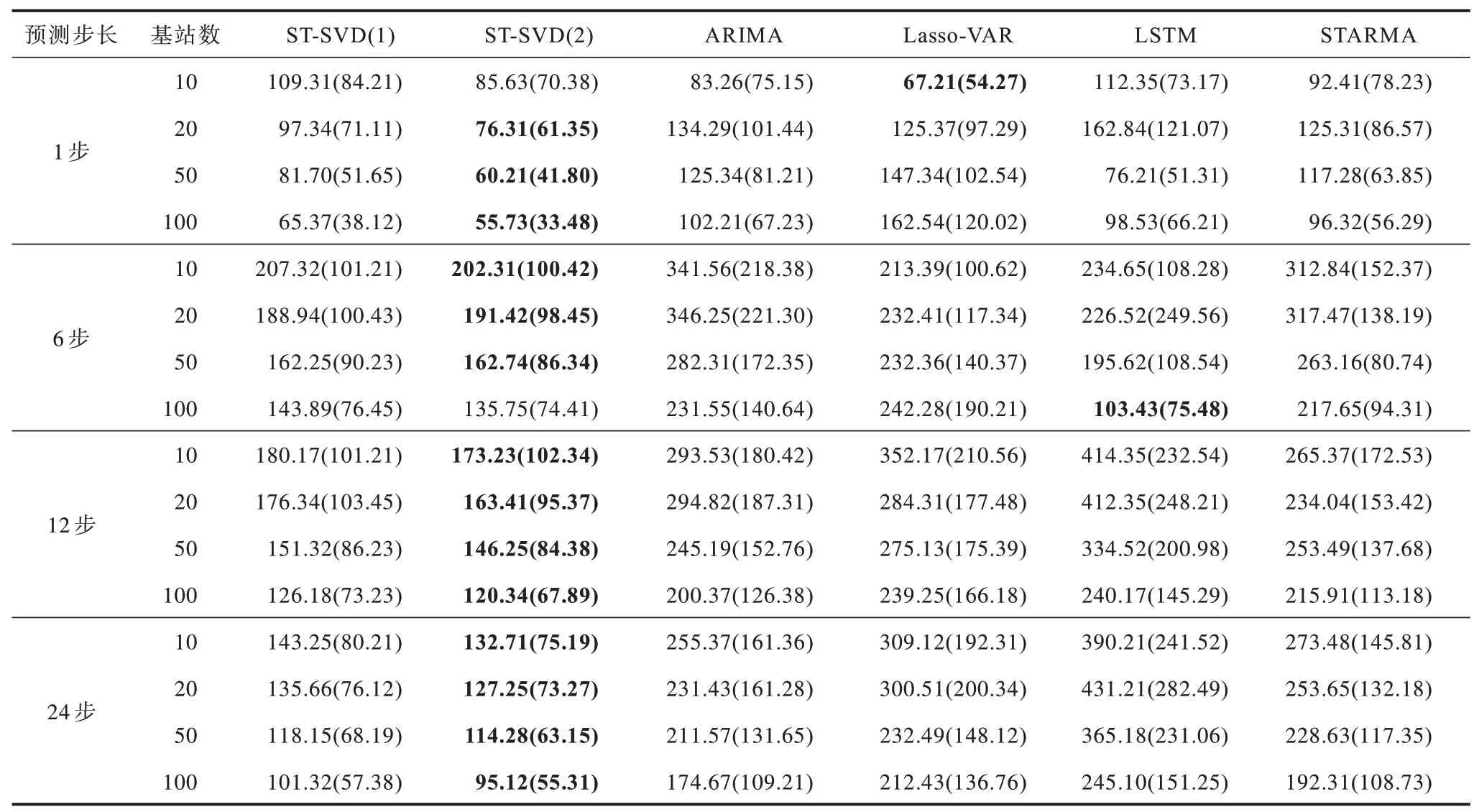
表5 6 种模型在不同基站个数与预测步长情况下的实验结果Table 5 Experimental results of six models under different number of base stations and different prediction step size

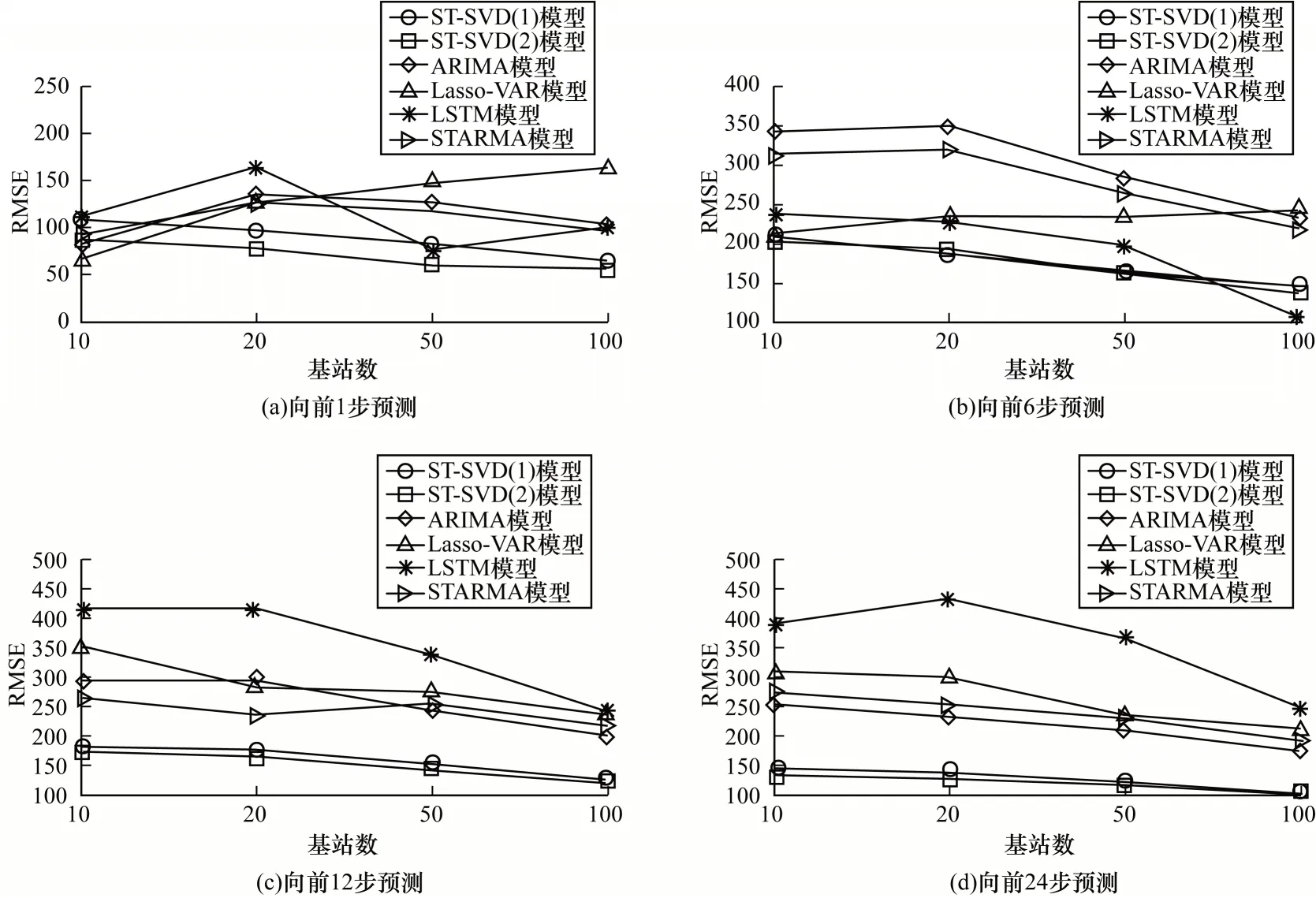
图9 6 种模型在不同基站个数与预测步长下的RMSEFig.9 RMSE of six models under different number of base stations and different prediction step size

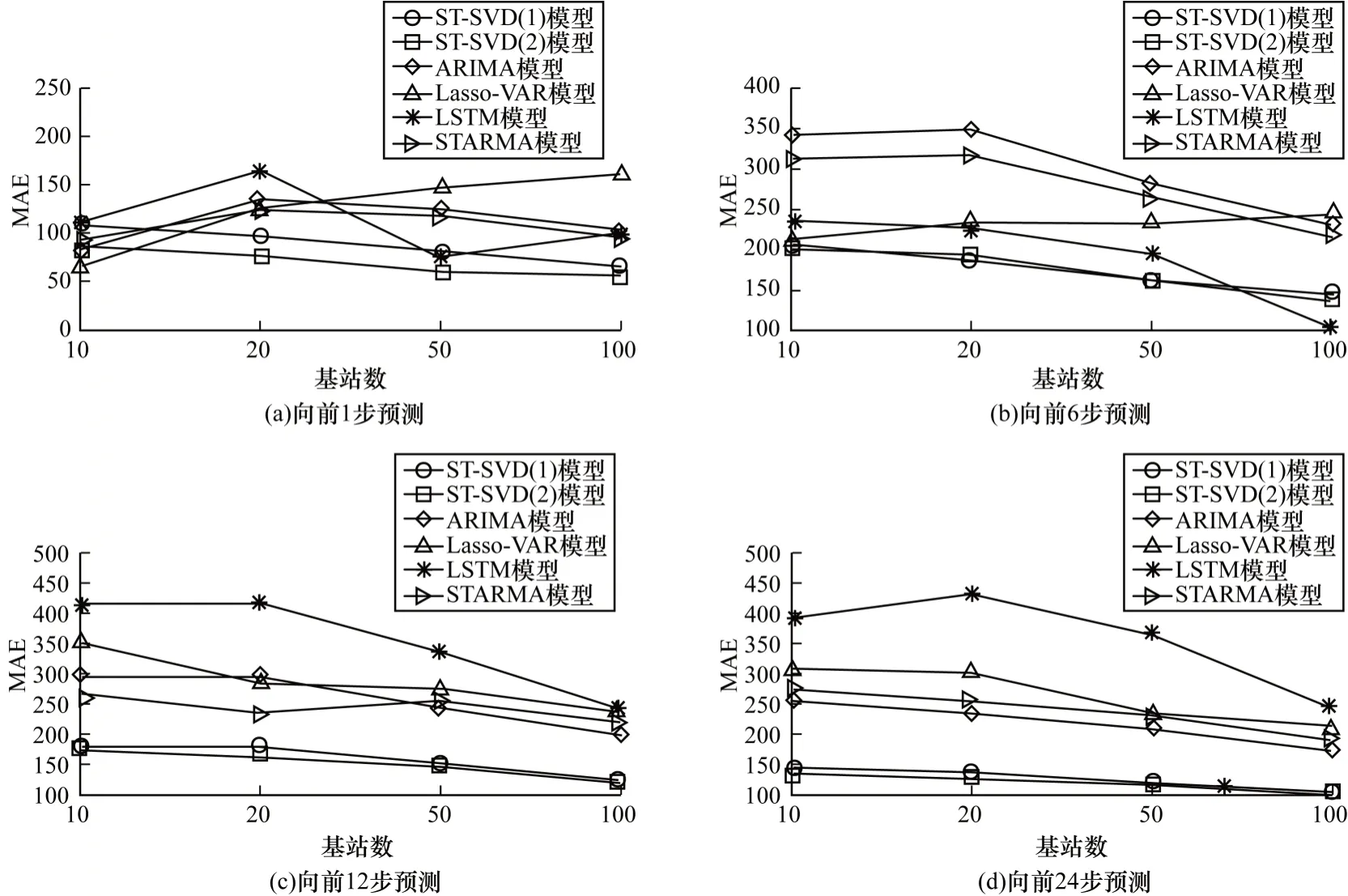
图10 6 种模型在不同基站个数与预测步长情况下的MAEFig.10 MAE of six models under different number of base stations and different prediction step size

4 结束语

时空序列模型STARMA 通过构建空间权重矩阵来表征数据的空间相关模式，但是空间权重的构建大多依赖距离等主观性因素，导致STARMA 难以适用于多数数据集。本文建立一种新的时空序列模型ST-SVD，其利用SVD 技术对时空数据集的时间模式和空间模式进行自动分解，通过ARIMA 模型拟合时间模式并建模预测，最终重建出时空预测结果。ST-SVD 模型不需要对数据集的空间结构进行假设，只需对时间序列实现建模，大幅降低了问题复杂度和模型训练成本。实验结果表明，ST-SVD 模型的预测效果优于LSTM、STARMA 等时空序列模型。但是，本文研究尚存在一定不足，一是ST-SVD 认为空间模式是时不变的，即空间作用和时间作用相互独立，二是在奇异值分解后的时间序列建模中利用了较为传统的ARIMA 模型，该模型是一种线性模型，无法捕捉到时间序列中的非线性模式。下一步将利用机器学习、深度学习等技术对时间模式进行建模，然后通过奇异值分解重建时空序列，以解决上述问题。