移动边缘计算中基于Lyapunov 的任务卸载与资源分配算法

唐 伦，胡彦娟，刘 通，陈前斌

（重庆邮电大学通信与信息工程学院移动通信技术重点实验室，重庆 400065）

0 概述

随着移动通信技术和互联网的快速发展，虚拟现实、增强现实和人脸识别等具有计算密集、时延敏感等特性的应用不断出现［1-2］。然而，由于终端设备在计算能力和电池寿命方面存在一定的局限性，导致它们难以支持上述应用［3］。受软件定义网络（Software Defined Network，SDN）和网络功能虚拟化（Network Function Virtualization，NFV）的驱动，移动云计算（Mobile Cloud Computing，MCC）技术应运而生，其允许用户将计算密集型任务卸载到资源丰富的远端云服务器执行，以缓解终端设备资源受限与高性能任务处理需求之间的冲突［4-5］。但是，在实际情况中，云服务器一般距离用户较远，云计算方案难以适用一些时延敏感的应用。为了解决这一问题，移动边缘计算（Mobile Edge Computing，MEC）技术被提出［6］，它能够在靠近移动设备的网络边缘提供云资源，不仅可以满足时延敏感型应用的QoS 需求，而且还在一定程度上降低了计算密集型应用所带来的网络负载和设备终端能耗［7-8］。

目前，已有学者针对MEC 任务卸载与资源分配问题进行研究。文献［9］考虑信道状态和任务到达的随机性，研究MEC 系统中能量效率与时延的权衡问题。文献［10］针对正交频分多址的移动边缘网络，设计一种基于计算能效的资源分配方案。文献［11］以最小化移动设备和MEC 服务器的平均总功耗为目标，提出一种在线无线资源和计算资源管理算法。文献［12］引入能量和时延加权因子，提出一种能量感知的卸载方案。虽然上述研究在一定程度上降低了任务时延和系统能耗，但考虑的均是单MEC 服务器场景下的资源分配问题，存在一定的局限性。在多服务器的MEC 系统场景下，文献［13］提出一种以最小化服务成本、最大化服务终端数量为目标的任务卸载和资源分配算法，文献［14］以最小化设备能耗和任务时延为目标，提出一种两层博弈论的贪婪卸载方案，文献［15］研究任务卸载和资源分配的联合优化问题，以降低设备能耗为目标，分别设计基于分支界定算法的最优方案以及基于组合算法的次优方案，这些方案更适用于实际边缘计算网络场景。此外，文献［16-17］将MEC 与能量收集技术相结合，研究卸载策略与资源分配问题。然而，上述基于平均值设计的MEC 系统难以满足低时延、高可靠的业务需求。文献［18］虽然保证了用户低时延、高可靠的需求，但是其忽略了对MEC 服务器计算资源的优化，从而提高了执行任务所消耗的功率成本并最终影响MEC 的系统收益。

考虑到任务到达的随机性，本文建立一种任务队列动态调度模型。为了满足用户对时延和可靠性的需求，对任务队列施加概率约束并建立最大化MEC 系统平均收益的资源优化模型。在此基础上，利用马尔科夫不等式［19］将概率混合优化问题转化为非概率优化问题，通过Lyapunov 优化理论将不同时隙下的耦合优化问题转化为3 个子问题并分别进行求解，以得到最优任务卸载与资源分配方案。

1 系统模型与问题建模

1.1 系统场景

MEC 系统场景如图1 所示，其由M个用户、S个基站和多个MEC 服务器组成。其中，每个用户通过无线链路关联到距离其最近的基站，每个基站通过有线链路连接一个配备多CPU 内核的MEC 服务器［11，18］。为了方便分析，本文假定用户计算任务由一个MEC 服务器处理，不考虑任务在服务器之间转发。本文将网络运行时间划分为若干个时隙，用Γ={0，1，…}表示网络运行的时隙集合，其中，定义每个时隙t的时间长度为τ。考虑到任务到达的随机性，本文建立两级任务队列模型，即用户任务队列模型和MEC 服务器任务队列模型，以对计算任务的状态进行刻画。

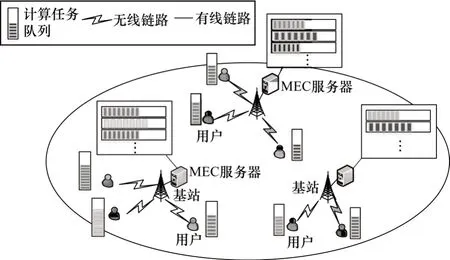
图1 移动边缘计算系统场景Fig.1 The system scenarios of mobile edge computing

1.2 用户任务队列模型

假设每个用户都有一个队列缓冲区，存储到达但未处理的计算任务。在每个时隙内，用户计算任务的到达过程是独立同分布的，且平均到达率为λi=E[Ai(t)]。同时，对于每个计算任务都可以选择在用户本地或者卸载到MEC 服务器进行处理。因此，本文定义时隙t时用户任务队列长度向量为Q(t)=[Q1(t)，Q2(t)，…，QM(t)]，Qi(t)的更新过程为：

其中，DΣ，i(t)为t时刻用户i所处理的总计算任务量，其具体表达式为：

式（2）等号右侧的第一部分为用户本地处理的计算任务量，fi(t)是用户i处理计算任务所分配的计算资源，即CPU 周期频率，Li表示执行每比特计算任务所需的CPU 周期；第二部分为卸载到MEC 服务器处理的计算任务量，R ij(t)是t时刻用户i卸载计算任务到MEC 服务器j时的传输速率，其表达式为：

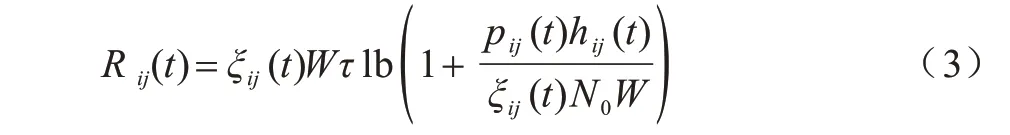
其中，W为MEC 服务器的带宽，ξij(t)表示MEC 服务器j为用户i分配的带宽比例，pij(t)和hij(t)分别表示从用户i到MEC 服务器j的传输功率和信道增益，N0为高斯白噪声的功率谱密度。另外，由于每个基站都连接一个MEC 服务器，因此在本文中j∈S同时表示MEC 服务器。

任务请求具有动态性，可能出现任务队列长度超出用户缓存空间的情况，从而导致数据包的丢失。因此，为了满足低时延、高可靠的任务需求，本文对用户队列长度添加概率约束［20］，即：

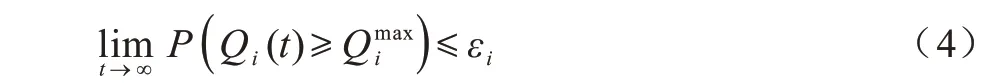
1.3 MEC 服务器任务队列模型

每个MEC 服务器中有多个队列缓冲区，可以同时存储多个用户卸载但尚未由MEC 服务器处理的计算任务。本文定义MEC 服务器j中用户i的任务队列为Xji(t)，其更新过程为：

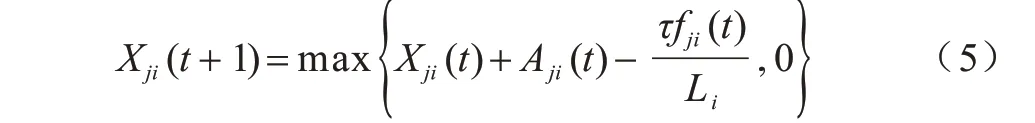
本文同样对MEC 服务器任务队列长度添加概率约束，即：

1.4 问题建模

1.4.1 时间平均吞吐量

由式（1）可得t时刻用户i所处理的计算任务量为DΣ，i(t)，将其记为t时刻系统用户i的吞吐量，相应的用户i时间平均吞吐量定义为Di，其表达式为：

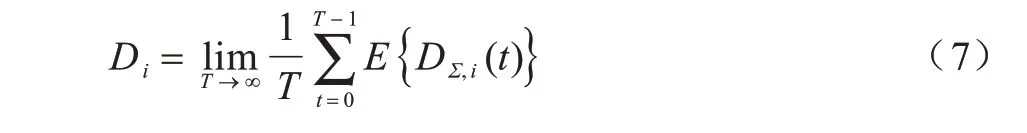
进一步定义MEC 系统的时间平均收入为：

其中，αi表示处理用户i任务的单位收入。

1.4.2 时间平均功耗

由式（2）、式（3）可知，用户i在t时刻的处理功耗和传输功耗分别为：

其中，κ是与芯片结构相关的有效系数［17］。用户i的时间平均功耗可表示为：

由式（5）可知，MEC服务器j在t时刻的处理功耗为：

则MEC 服务器j的时间平均功耗可表示为：

基于上述用户和MEC 服务器的时间平均功耗，可定义用户和MEC 服务器的时间平均功率消耗成本分别为：

其中，β和γ分别表示用户和MEC 服务器的功率单位成本。

1.4.3 优化模型

本文设计一种联合功率、带宽以及计算资源的分配算法，以在满足低时延、高可靠业务需求的同时最大化MEC 系统的时间平均收益。时间平均收益指系统中所有用户任务的时间平均收入与用户和MEC 服务器时间功率消耗成本的差值，其优化模型如下：

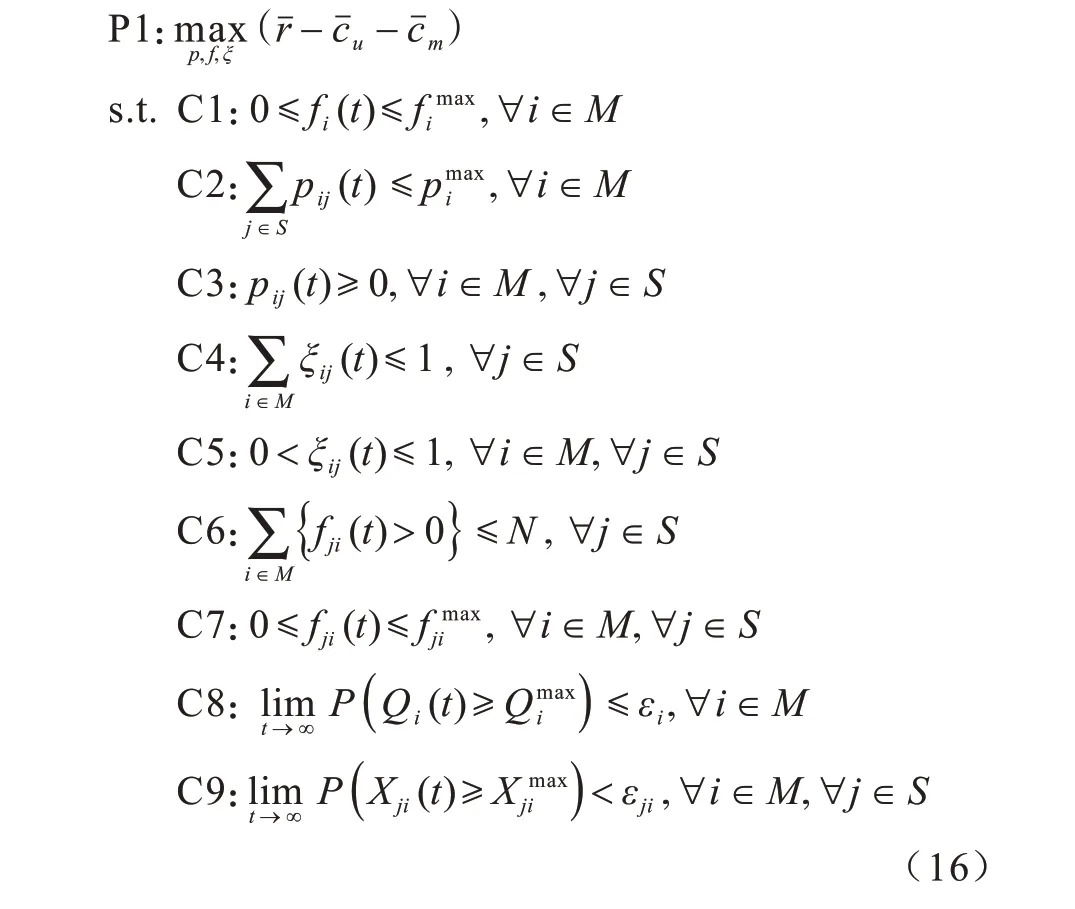
约束条件说明：C1 表示为用户分配的计算资源不能超过总的计算资源C2 和C3 表示用户的传输功率约束；C4 和C5 表示MEC 服务器j分配给用户i的带宽比例约束；C6 表示在MEC 服务器中并行处理用户任务队列的数量不能超过CPU 总核数N；C7 表示MEC 服务器j分配给用户i的计算资源不能超过单个CPU 核的最大资源值；C8 和C9 分别表示用户任务队列上溢概率和MEC 服务器任务队列上溢概率。

2 资源优化问题转化

2.1 概率混合问题转化

由上述优化模型可得问题P1 是一个概率混合优化问题，其分析处理具有一定难度。因此，本文引入马尔科夫不等式，对概率约束进行转化［20］。

定义1（马尔科夫不等式）若X是一个非负随机变量，a＞0，则

利用定义1 可将约束C8 和C9 转化为：

其中，C8′和C9′为连续时隙的平均约束，而C1～C7 是单时隙的瞬时约束。传统方法难以处理不同时隙下的耦合问题，因此，本文利用Lyapunov 优化理论设计一种基于单时隙状态的资源分配方案。

2.2 基于Lyapunov 的优化理论分析

本文引入虚拟队列Yi(t)和Zji(t)对时间平均约束进行转化，虚拟队列更新方程分别为：

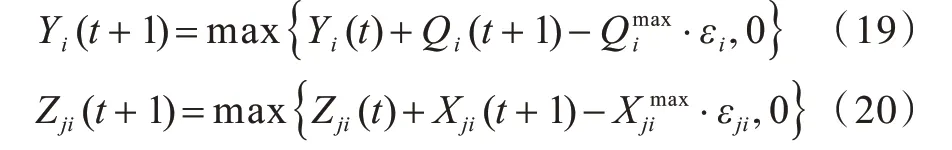
在t时刻系统的队列状态向量可表示为Θ(t)=[Yi(t)，Zji(t)]，进而定义Lyapunov 函数为：

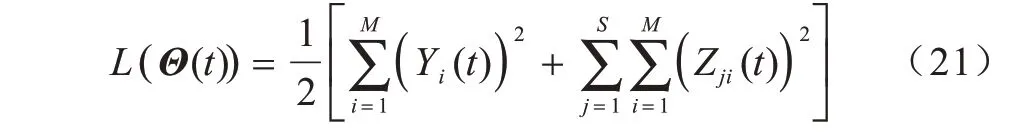
式（21）表征了系统中的队列拥塞程度，函数值越大，队列越长，相应的用户任务处理等待时间就越长。因此，为了缩短用户的等待时延，保持系统的稳定性，本文定义单时隙Lyapunov 偏移为：

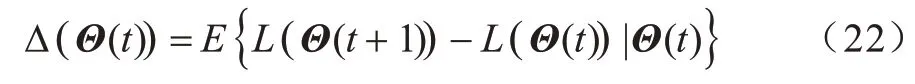
在优化理论中，Lyapunov 偏移通常用来进行资源分配策略选择，为其添加一个加权代价函数，从而得到Lyapunov 偏移加罚。本文的Lyapunov 偏移加罚定义为单时隙Lyapunov 偏移与该时隙MEC 系统时间平均收益期望的加权差，即：

其中，V为权衡偏移函数与代价函数的非负控制参数，ζ为一个有限正常数，Dji(t)大小为

进一步将问题P1 转化为最小化Lyapunov 偏移加罚上界的问题，即最小化式（23）的右侧，得到：

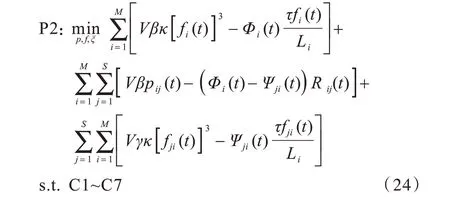
在优化问题P2中，Φi(t)=Vαi+Qi(t)+Yi(t)，Ψji(t)=Xji(t)+Zji(t)。

3 计算资源与无线资源联合分配方案

由文献［11，21］可知，问题P2 可以转化成3 个子问题，即用户本地计算资源分配问题P2.1、功率与带宽资源分配优化问题P2.2 以及MEC 服务器的计算资源分配问题P2.3。

3.1 用户本地计算资源分配问题

根据式（24）可得用户本地计算资源分配问题如下：

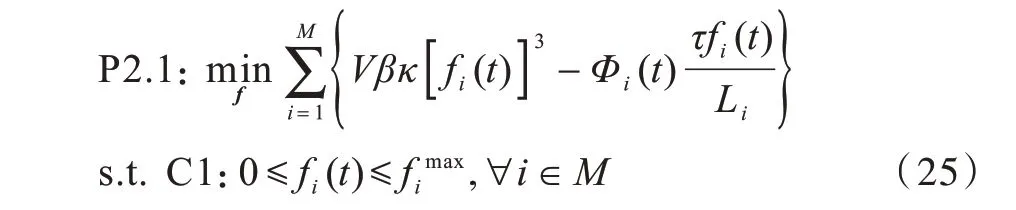
从式（25）可以看出，问题P2.1 是一个凸优化问题，而且其目标函数和约束条件都可以对fi(t)进行分解，因此，可对每个fi(t)进行优化。本地计算资源最优解(t)可表示为：

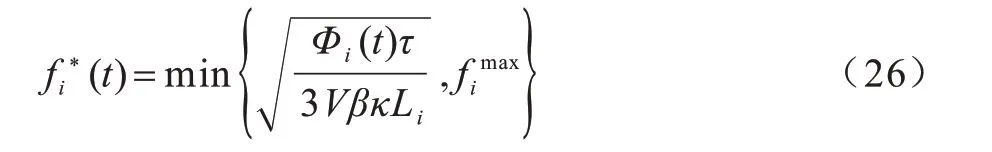
3.2 功率与带宽资源分配优化问题

与无线资源相关的系统决策包括任务卸载的发射功率分配和带宽分配，因为两者为常数，所以难以适应时变的系统状态［11］，因此，本文对问题P2 中的带宽约束C5 进行修改，如下：

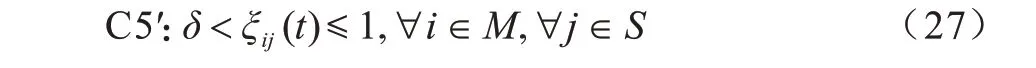
其中，δ为带宽分配的最小比例，其取值范围为Mj表示接入基站j的用户数量。根据式（24）、式（27）可将P2.2 优化问题转化为：

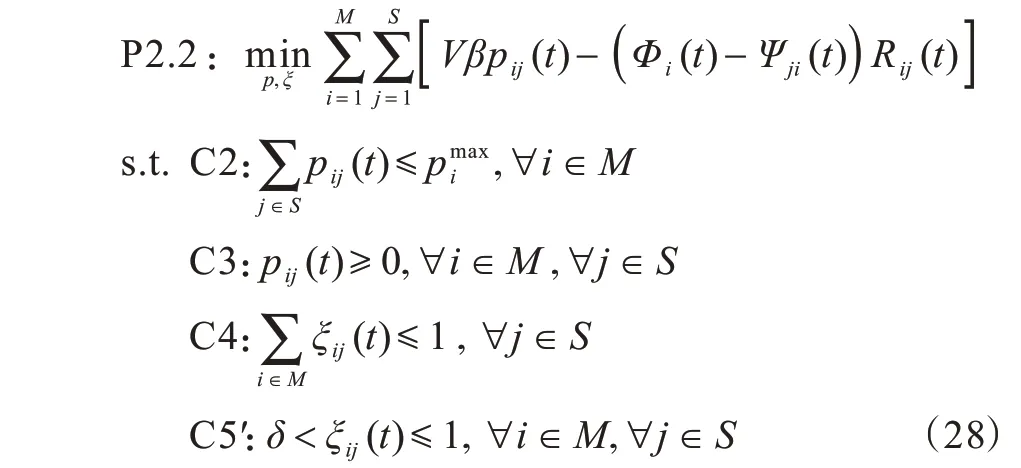
当Φi(t)-Ψji(t)≤0 时，问题P2.2 的目标函数随pij(t)的增大而增大。当pij(t)=0 时，问题P2.2 取最小值。令M′(t)表示Φi(t)≤Ψji(t)的用户集合，最优功率为(t)=0，最优带宽比例为(t)=δ。

当Φi(t)-Ψji(t)＞0 时，优化问题变成一个凸优化问题。令(t)表示Φi(t)＞Ψji(t)的用户集合，因此，子问题P2.2 可简化为：

子问题P2.2′的目标函数中含有2 个变量，若利用一般的凸优化方法，算法有较高的复杂性。因此，本文将子问题P2.2′解耦为功率分配与带宽分配2 个子问题，通过多次迭代得到最优资源分配方案。

3.2.1 功率分配子问题

给定带宽分配比例，用户的功率资源分配问题可表示为：

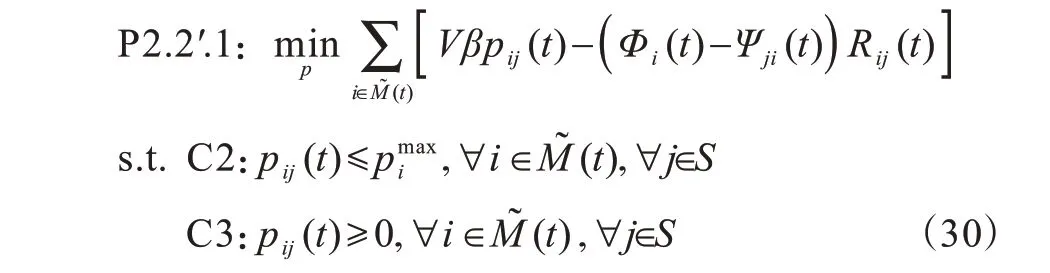
类似于问题P2.1，本文对每个用户的功率进行优化，得到：

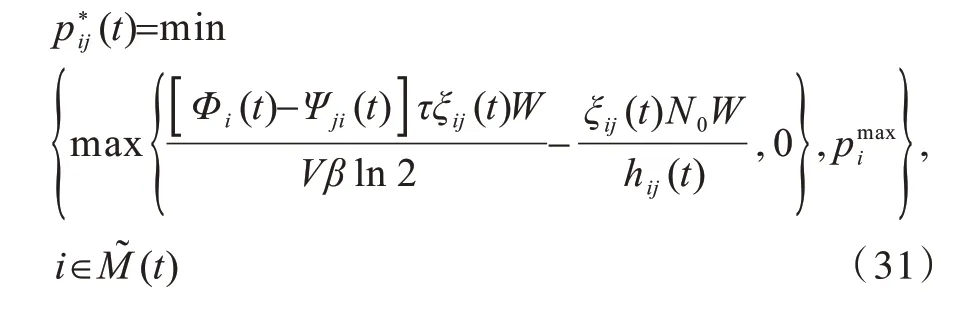
3.2.2 带宽分配子问题

给定功率分配方案，用户的带宽资源分配问题可表示为：

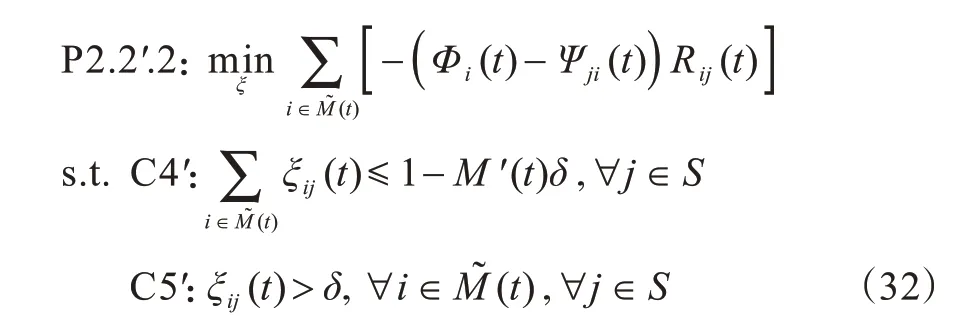
子问题P2.2′.2 是一个凸优化问题，联合目标函数和约束条件可得到对应的拉格朗日函数，表示为：

其中，μ为约束条件对应的非负拉格朗日乘子。进一步，通过L(ξ，μ)对ξ求偏导数得到：

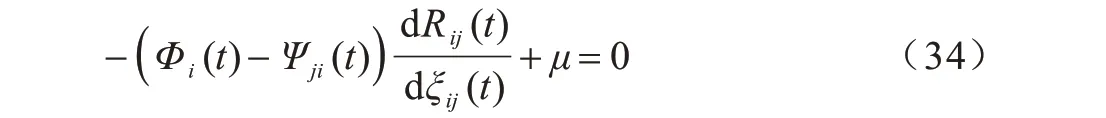
定义Gi(μ)为式（34）的解，因此，可以利用KKT条件得出最优解，其中，最优带宽分配ξ*和最优拉格朗日乘子μ*满足：

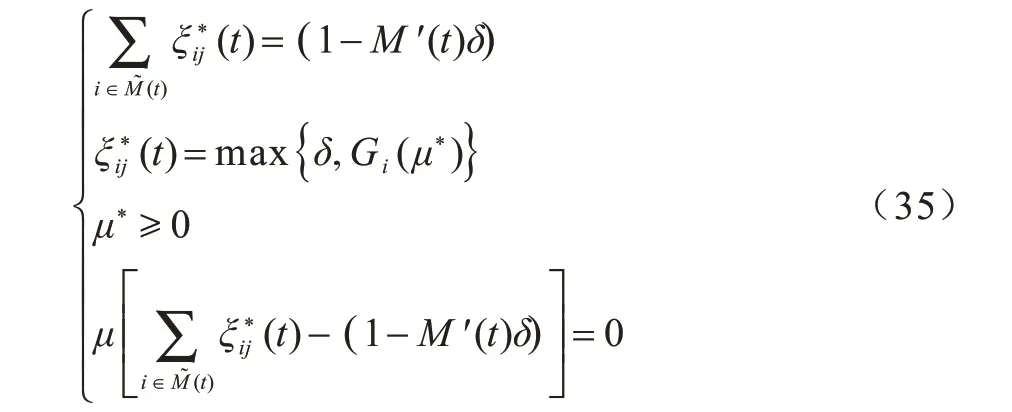
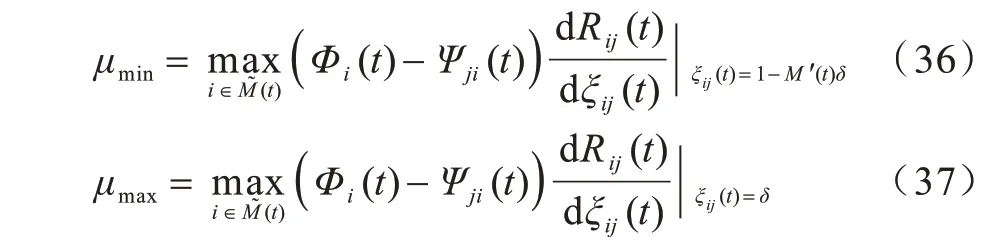
进一步利用二分搜索法得到μ的最优解并代入式（35）中，从而得到带宽分配方案。

3.3 MEC 服务器计算资源分配问题

根据式（24）可以得到MEC 服务器的计算资源分配问题，如下：

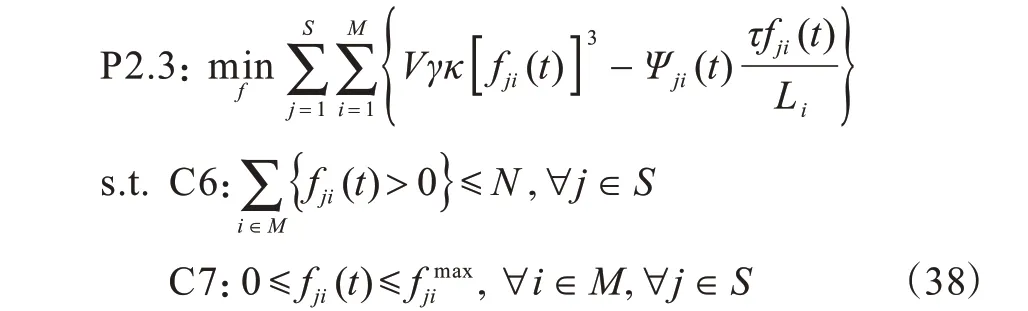
由于约束条件C6 是一个离散约束，导致P2.3 问题是一个非凸优化问题，但是，当忽略约束条件C6时，该问题是一个线性问题且目标函数和约束条件都可以对fji(t)进行分解。因此，本文首先对fji(t)进行优化，得到初始计算资源分配方案，然后将得到的资源分配方案代入约束C6 中，判断是否满足约束，若满足即得到最终解；否则，在初始解中依次选择对目标函数贡献最小的用户，收回计算资源，即将fji(t)设置为0，直到满足约束C6。MEC 服务器计算资源分配算法描述如算法1 所示。

算法1MEC 服务器计算资源分配算法

3.4 本文算法描述

结合3.1 节～3.3 节的分析，基于Lyapunov 的任务卸载与资源分配算法描述如算法2 所示。该算法是一个2 层迭代算法：外层循环是移动边缘计算系统内的用户队列、MEC 服务器队列以及虚拟队列的更新；内层循环是对任务卸载与资源分配的3 个子问题求解。

算法2基于Lyapunov 的任务卸载与资源分配算法

4 仿真结果与分析

为了验证本文所提算法的有效性，在一个400 m×400 m 的区域内均匀部署4 个基站和N个用户，其中，每个基站都配备一个CPU 核数为8 的MEC 服务器。将本文算法与基于Lyapunov 优化的在线联合任务卸载与资源分配（OJ-TORA）算法［13］、基于时延与可靠性感知的任务卸载与资源分配（LRA-TORA）算法［18］以及任务全部本地执行（Non-MEC）算法和任务全部卸载到MEC 服务器执行（Fully-MEC）算法2 个基线算法进行比较。参考文献［22］，本文的路径损耗模型定义为h=127+30 logad，d的单位为km。考虑到用户所到达的任务与用户所消耗功率以及MEC 所消耗功率的量级不同，因此，在文献［21］收益和成本参数的基础上对本文参数进行设置，单位任务收入为1×10-3unit/bit，单位功率成本为0.2 unit/W。本文其他仿真参数设置如表1 所示。

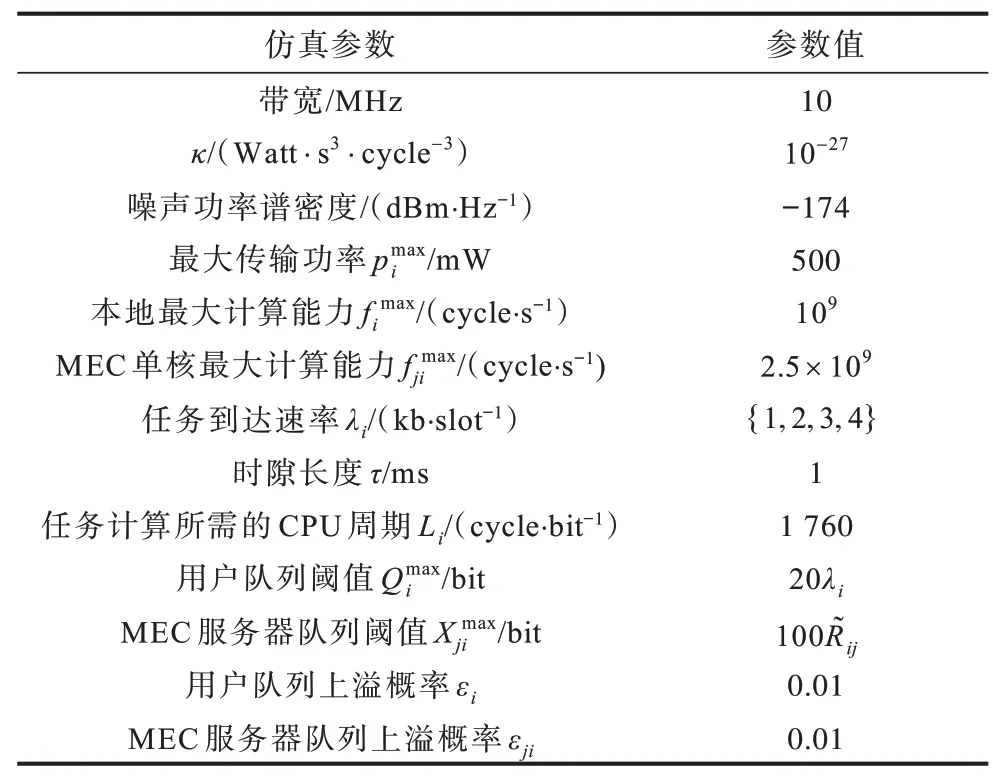
表1 仿真参数设置Table 1 Simulation parameters setting

图2 所示为用户数为40 时MEC 系统时间平均收益随控制参数V的变化情况。从图2 可以看出，时间平均收益随控制参数V的增加而逐渐增大并趋于平稳，这是因为在Lyapunov 优化过程中，控制参数V越大，则系统越倾向于优化罚函数，即系统时间平均收益，该结果验证了本文所提算法的有效性。

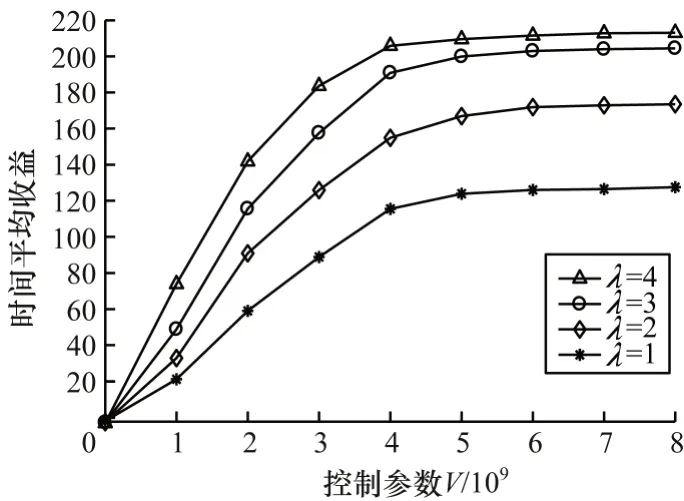
图2 系统时间平均收益和控制参数V 的关系Fig.2 The relationship between system time average profit and control parameter V

图3 所示为不同算法下任务到达率与系统时间平均收益的关系。从图3 可以看出，系统时间平均收益随着任务到达率的增大而增大，而且对于任意任务到达率，本文算法在所有算法中收益最高。这是因为本文综合考虑功率、带宽资源以及计算资源并进行优化，能在满足用户QoS 需求的同时合理地分配任务资源。

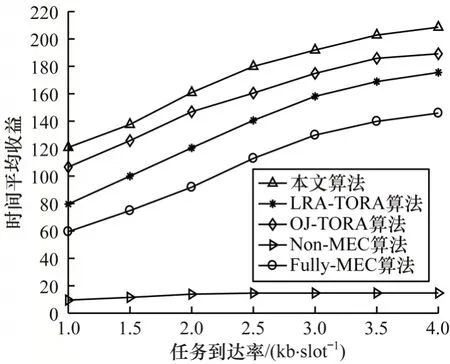
图3 系统时间平均收益和任务到达率的关系Fig.3 The relationship between system time average profit and task arrival rate

从图4 可以看出，本文算法相比其他3 种算法平均端到端时延更短，说明本文算法在当前业务激增的网络环境下具有较好的时延性能。此外，Fully-MEC 算法相比其他算法平均端到端时延最长，这是因为其他3 种算法考虑了用户本地执行，在一定程度上缩短了时延。

图4 平均端到端时延和任务到达率的关系Fig.4 The relationship between average end-to-end delay and task arrival rate

图5 所示为不同算法下系统时间平均收益与用户数的关系，从图5 可以看出，4 种算法的系统时间平均收益都随用户数的增加而增加，但是当用户数大于40后，收益的增长速率变缓。由于本文算法在分配带宽资源时根据用户实际需求动态分配而非均等划分，提高了系统任务的收入，另一方面，该算法根据任务队列状态对MEC 服务器的计算资源进行分配，提高了资源利用率，节约了系统成本。因此，本文算法在系统时间平均收益上明显优于其他3 种算法。

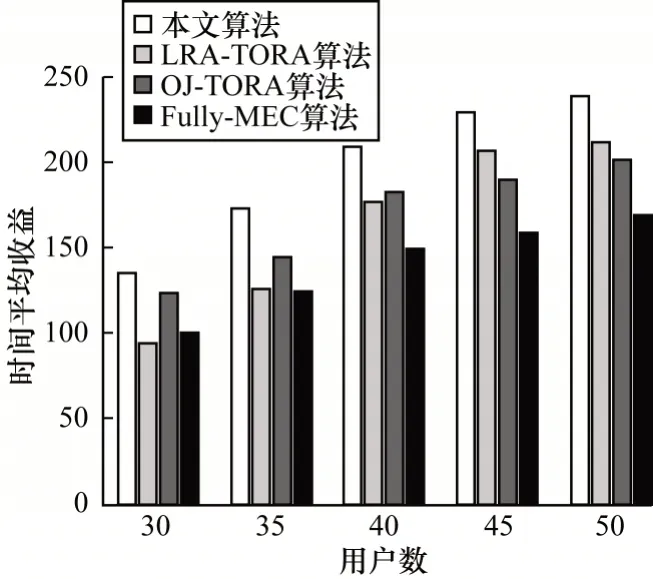
图5 系统时间平均收益与用户数的关系Fig.5 The relationship between system time average profit and the number of users

由于队列长度是评估用户时延和数据可靠性的关键因素，因此本文对任务队列长度的互补累积分布函数（CCDF）进行仿真，并将本文算法与LRATORA 和OJ-TORA 算法进行对比。当任务到达率为3 kb/slot 时，定义用户队列阈值和MEC 服务器队列阈值分别为6×104bit 和5×105bit，平均队列长度CCDF 如图6 所示。从图6 可以看出，OJ-TORA 算法用户队列和MEC 服务器任务队列长度CCDF 都高于本文算法和LRA-TORA 算法，其可靠性最差。本文算法用户任务队列长度CCDF 均小于其他2 种算法，而MEC 服务器任务队列长度CCDF 略高于LRA-TORA 算法，但并未超过队列阈值，因此，本文算法仍具有较好的可靠性。

图6 3 种算法的任务队列长度CCDF 对比Fig.6 Comparison of task queue length CCDF of three algorithms

5 结束语

本文基于Lyapunov 优化理论，提出一种最大化MEC 系统时间平均收益的任务卸载与资源分配算法。该算法在多MEC 服务器多用户系统模型下，建立任务队列动态调度模型并为队列施加概率约束，在保证用户时延和可靠性需求的同时对无线资源和计算资源实现联合分配。同时，利用马尔科夫不等式以及Lyapunov 优化理论将优化问题转化为3 个子问题并进行求解。仿真结果表明，该算法在时延、可靠性以及系统收益方面均具有较好的性能表现。下一步将对动态场景下的任务卸载与资源分配问题进行研究。