发动机环形混流装配线多目标排序方法

张家骅，李爱平

（1.同济大学机械与能源工程学院，上海201804；2.无锡工艺职业技术学院机电与信息工程学院，江苏宜兴214206）

随着社会对产品个性化、多样化需求的不断提高，企业采用混流装配线在同一条装配线上生产多种产品。混流装配线可以降低库存，满足顾客的多样化与个性化需求，缩短产品的上市时间，提高企业的竞争力。近年来，汽车企业开始采用混流装配线生产发动机，以应对激烈的市场竞争［1-3］。

随行托盘作为装配线辅助机具，被许多发动机企业所采用来起到输送、定位和辅助自动装配发动机的作用。为了降低投入成本，便于托盘在生产过程中循环使用，需要布置环形装配线，让托盘能回流到装配线起始工位。在发动机环形装配线上，托盘数量是固定的。面对动态、激烈的市场，企业通过开发多款发动机共用托盘，实现了发动机环形装配线的混流生产。

要使混流装配线有效运行，混流装配线排序是需要解决的关键问题之一，该问题一直是学术界和企业界的研究重点［4-5］。针对直线型、双边型和U型等混流装配线，目前已有大量研究结果［6-8］。但这些研究均没有考虑发动机装配线的实际特点，无法直接应用到实际生产中。王炳刚［1］虽然开展了发动机混流装配线排序问题的研究，但只考虑缓冲区容量约束，没有考虑托盘数量约束。由于托盘数量对闭环制造系统有重要影响［9］，因此该方法不能直接应用到发动机环形混流装配线排序上。

为了保证发动机环形混流配线的有效运行，本文针对该类装配线的排序问题开展研究，提出了一种自适应多目标遗传算法和离散事件仿真相结合的多目标排序方法。采用本方法，可以得到一组可行的产品投产排序方案，指导企业安排生产。

1 环形混流装配线解析-仿真模型

图1 为典型的汽车发动机总装配线。该线有1条环形主装线和1条部件分装线组成，主装线上有1个并行设备工位，发动机托盘在环形主装线上进行循环。现有的混流装配线排序方法，通过建立精确的解析模型求解可行的排序方案，但解析模型往往简化了研究对象的复杂生产特点。对于具有固定数量托盘的环形装配线，现有研究表明，只有离散事件仿真是该类装配线最有效和最精确的研究方法［9-10］。因此，为了得到发动机环形混流装配线排序方案，本文通过结合离散仿真方法，建立了解析-仿真混合模型。

图1 典型的汽车发动机装配线Fig.1 Classic engine assemble line

1.1 问题描述

发动机环形混流装配线由多个工作站和线上缓冲区组成，通过线上缓冲区将装配线布置成环形（见图1），装配线上的托盘数量固定。装配线上混合装配P种产品，在一个计划期内，对第p（p=1，2，…，P）种产品的需求量为Dp，则对所有产品的总需求量为生产采用最小生产循环（Minimal Production Set，MPS）策略：h表示各种产品需求量Dp（p=1，2，…，P）的最大公约数；dp=Dp/h表示一个MPS内生产产品p的数量为一个MPS内个P种产品的总生产量。当p种产品按照一定顺序以最小生产循环投入装配线时，循环次数h，即完成最终的生产需求。

1.2 最小化零部件消耗速率波动

汽车行业中，为了降低库存和减少在制品数量，关键零部件使用速率均匀化是准时化（Just in Time，JIT）生产方式的基本要求［12］。最小化零部件消耗速率波动的解析模型如下：

式中：k为第k个生产阶段，k=1，2，…，d；r为零件的种类，r=1，2，…，R；xp，k为k个生产阶段中产品p的累积量；cr，p为产品p需要零件r的数量；dp为第p种产品的需求量；sp，k为p在第k个阶段生产sp，k=1，否则为为在前第k个产品零部件实际消耗率是k阶段理论零部件消耗率。式（2）表示xp，k等于k个位置中产品p的累积量，式（3）表示在投产的顺序中每个位置只能有一个产品，式（4）保证到k个阶段共生产k个不同产品。

1.3 最大化生产率

生产率是评价环形生产线的一个重要指标［4，14］，该目标可以表示为

本文采用仿真模型来获得环形混流装配线的生产率，图2为所研究的可同时生产三款发动机的环形混流装配线仿真模型。生产率采用的是每天的生产量（台/d）。

图2 发动机环形混装线仿真模型Fig.2 The model of the engine closed-loop line

仿真模型在离散事件软件Plant Simulation 14.0中建立，其中有两个Source对象：一个Source对象生成待装配产品，一个Source对象生成安放产品的托盘。

2 自适应多目标遗传算法

遗传算法被认为是求解混流装配线排序问题的一个有效的方法［14］。为了求解上文提出的解析-仿真混合模型，本文设计了一种内嵌离散事件仿真的自适应多目标遗传算法。图3为算法的具体流程图。

在该算法中，染色体按照产品投产顺序编码；将生成的染色体作为离散事件仿真模型的输入参数；离散事件仿真运行仿真模型后，返回生产量结果，与零部件消耗速率波动量一起进行适应度评估。算法的具体环节如下所述。

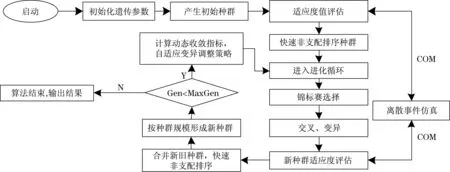
图3 自适应多目标遗传算法流程图Fig.3 Flow chart of the algorithm

2.1 编码方案和初始种群

采用整数或字母排列编码，每一种染色体编码方案对应一种排序方案。将一个最小循环生产循环（MPS）中的产品品种序号用有序整数进行标号，每一个产品种类对应一个实数，染色体中每一个基因值表示产品品种序号，染色体长度等于一个MPS的产品的总的需求量d。

例如，一个MPS中有8个3种不同品种的产品分别为3个品种1，3个品种2，2个品种3。品种1、品种2和品种3分别在染色体中用整数1、2、3表示，该排序方案可用图4所示染色体表示。初始种群按照设定的种群规模，采取随机方式生成。

图4 染色体编码示意图Fig.4 Encoding scheme of a chromosome

2.2 适应度值评估

本文共有两个优化目标：一个是最小化零部件消耗速率波动f1；一个是最大化生产量f2。算法采用保留最小适应度值方法，因此，f1和f2的适应度评估函数如下：

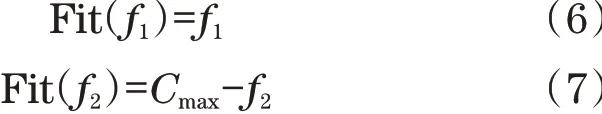
式中：Cmax为f2估计的最大值，经过多次模拟获得，本文为1 500台/d；Fit（f1）通过适应度函数计算获得，Fit（f2）由离散仿真软件获得。

2.3 组件对象模型（COM）技术

组件对象模型（Component Object Model，COM）提供了使多个影响程序或组件对象协同工作并互相通讯的能力。通过COM技术，可以实现离散仿真软件内嵌入混合遗传算法程序内，进行数据交换。

2.4 快速非支配排序

采用Pareto分层和拥挤距离机制对非支配解集进行排序，从而确定各个解之间的支配关系与优先关系。

2.5 竞标赛选择

从种群中随机选择2个个体，按照竞标赛规则进行适应值比较，适应值较大的个体被选择进入下一代。

2.6 交叉与变异算子

交叉算子采用双点交叉，对于第一个父代染色体P1，随机产生两个交叉点位置，交叉点内的基因位置和内容复制给子代S1。在父代P2中从前到后删去两个交叉点内相同内容，然后从前到后，将P2中的基因内复制给S1。调换P1和P2的操作，生成第二个子代S2。图5为双点交叉示意图。

图5 双点交叉示意图Fig.5 Scheme of two-point crossover

变异算子采用换位变异。任意选取染色体中的一个位置，将该位置的内容与染色体内其他位置进行互换，完成换位变异。如图6所示，选中的基因可以和染色中其他任意位置的基因互换。

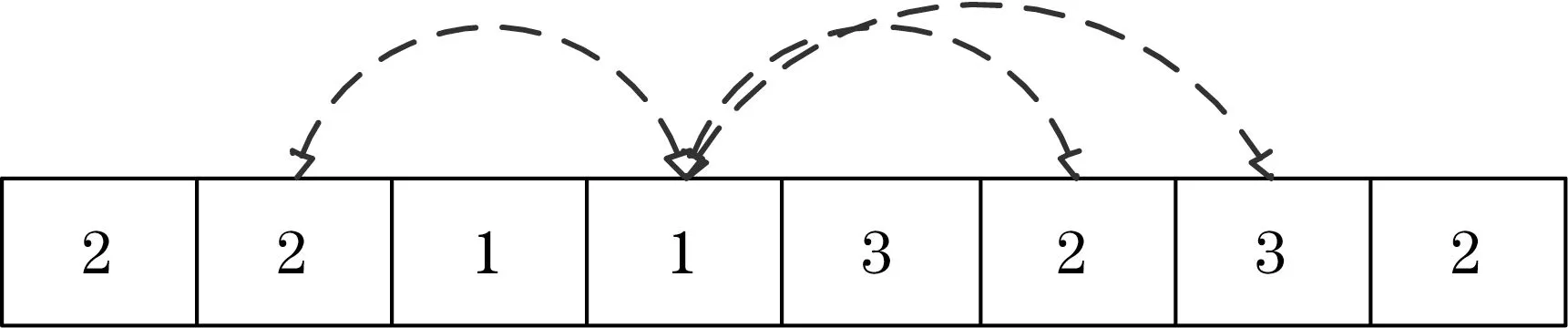
图6 换位变异示意图Fig.6 Scheme of swap mutation

2.7 自适应变异调整策略

遗传算法容易陷入局部收敛，为了提高算法的寻优能力，引入自适应变异调整策略。该策略通过判断算法的收敛程度，自动调整变异系数。

多目标解集S的收敛性可以用动态收敛性指标（CP）表示［15］：

式中：dti为解集S中的第i个解与上一代非支配解集中解T的最小Euclidean距离；CP∈［0，1］，如果CP接近0，说明算法逐渐收敛，通过增大变异概率，提高种群多样性。本文所用自适应变异策略如表1所示。

表1 自适应变异策略Tab.1 Scheme of the adaptive mutation

3 实例研究

3.1 实例描述

某厂发动机装配车间在一条环形混装线上混合生产三款分别是排量为1.0 T的3缸，和排量1.4 T、1.5 T的4缸发动机，产品型号用字母A、B、C表示。装配线由36个工位组成，采用端面摩擦积放式辊道传送托盘；工作站间的输送辊道还起到线上缓冲区作用；装配线上现有托盘数目100个，各种发动机在各个工作站的操作时间如表2所示，各发动机所需要的5C件（指凸轮轴、曲轴、连杆、缸体和缸盖）如表3所示，装配线布局图如图2所示。

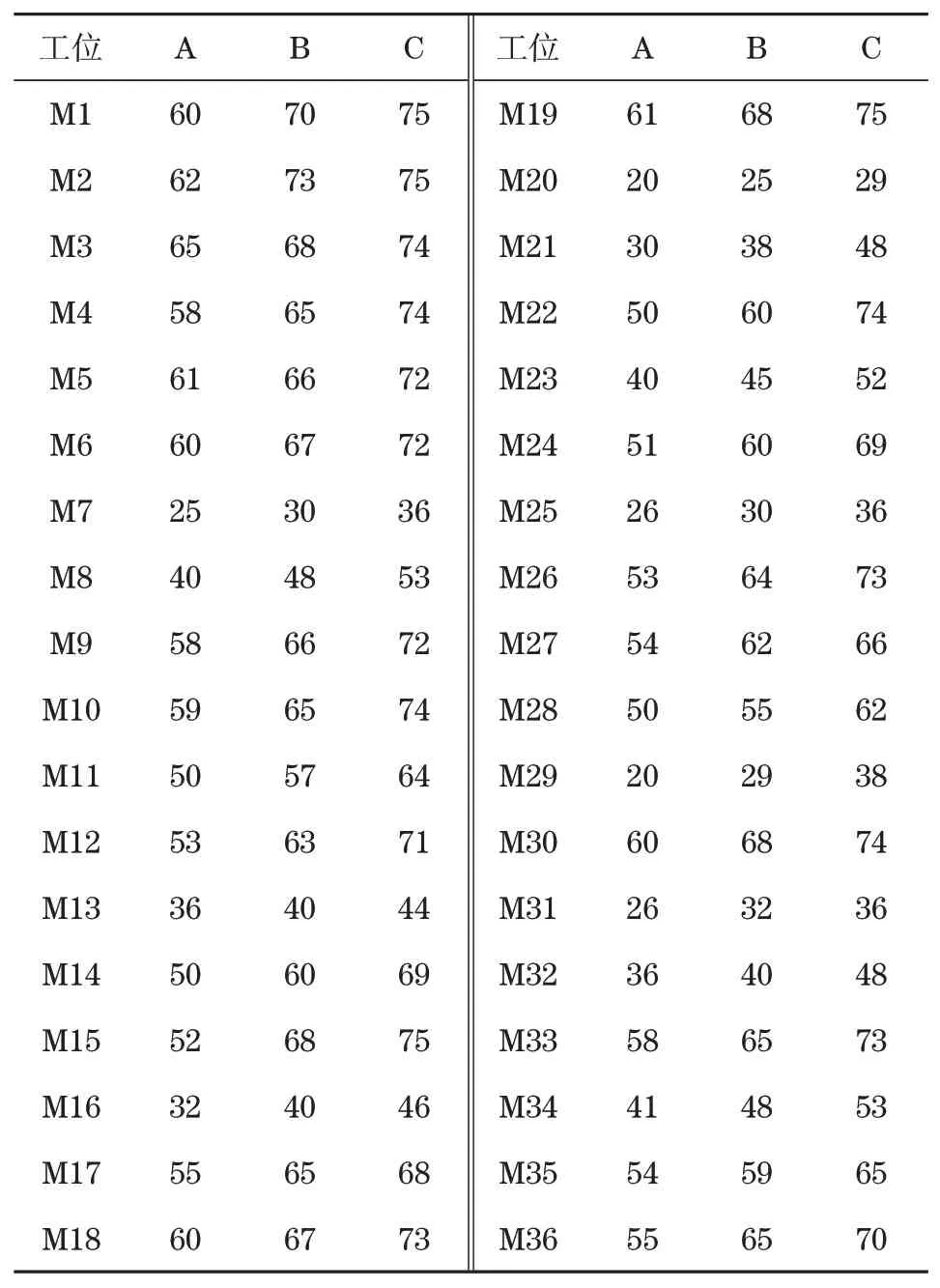
表2 产品操作时间Tab.2 Operation time of tasks s

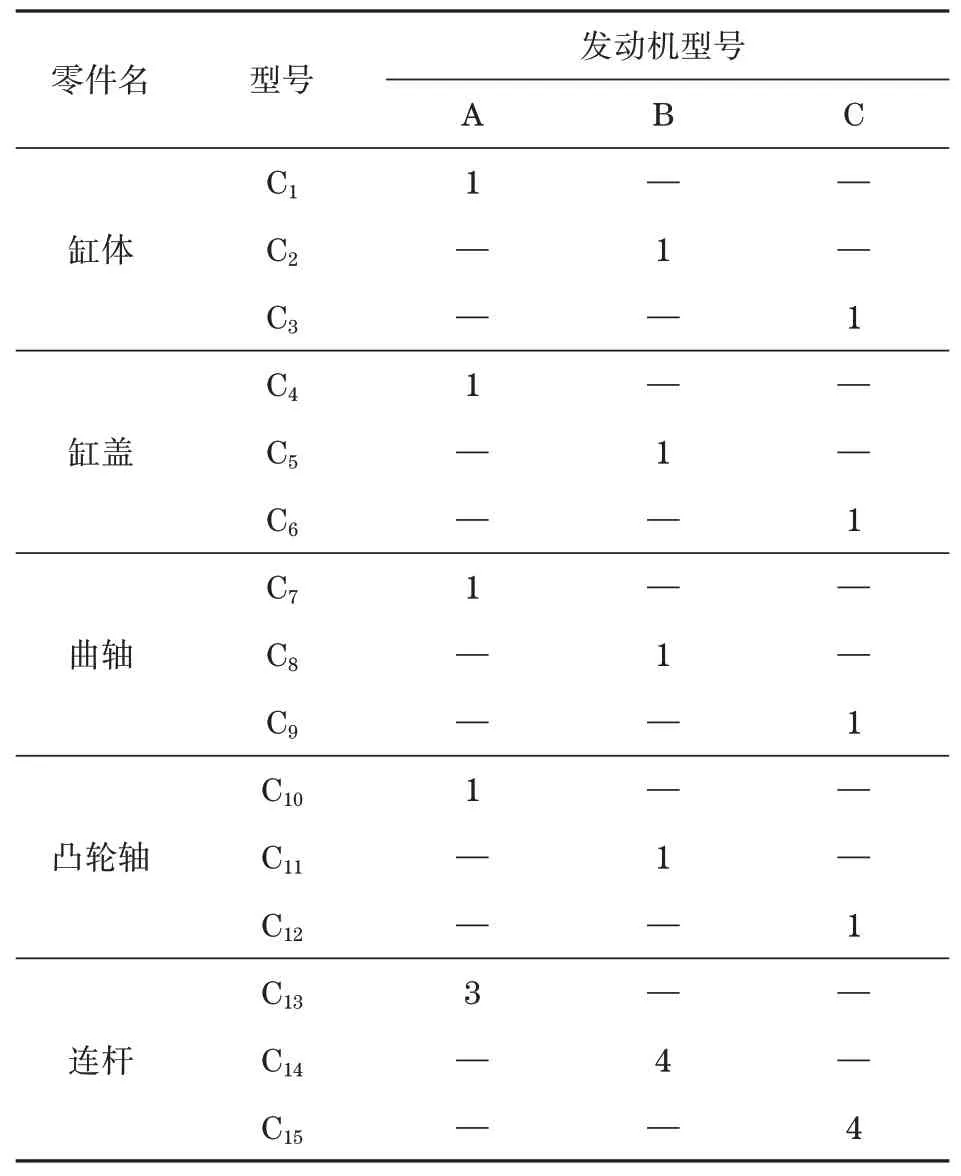
表3 产品5C件需求量Tab.3 The requirement of 5C

企业下达的某次计划MPS中A∶B∶C产品比例7∶5∶5，可得到该比例下车间每日装配产品可能的投产排序方案有(7+5+5)！(7！×5！×5！)=4 900 896种。装配车间需要在这些序列中，确定装配线上产品的投产顺序。

3.2 算法性能分析

程序采用Matlab进行编写，离散时间仿真软件采用Plant Simulation 14.0。经前期调试后，算法的参数设置如下：初始种群规模Pop=20，锦标赛选择竞赛规模Tour=2，交叉概率Pc=0.8，初始变异概率Pm=0.2，迭代次数Mg=100，离散事件仿真模拟时间24 h。

首先分析本文提出的自适应多目标遗传算法（AMOGA）的性能。图7为随着迭代所展现出的解的变化。进化开始时，解分布在零散区域内。随着进化代数的增加，解开始向前端聚集，从第10代可以看到，解已经在前端聚集；在第90代时，解基本已经到达前沿。从解的进化可以看到，这两个目标值是相互冲突的，不能同时优化两个目标。图8将AMGOA算法的两个适应度值与经典多目标算法NSGA-II计算的两个适应度值的收敛曲线进行了对比，其中NSGA-II采用了与本文相同的参数设置。图中可见，尽管适应度值2在两个算法中都收敛到相同的最优值，但是适应度值1采用本文的算法可以收敛到最小值100，而NSGA-II智能收敛到105，这是由于本文算法通过自适应变异策略，避开了局部最优，提高了算法的搜索性能。

图7 不同算法的Pareto结果比较Fig.7 Comparison of Pareto results of different algorithms

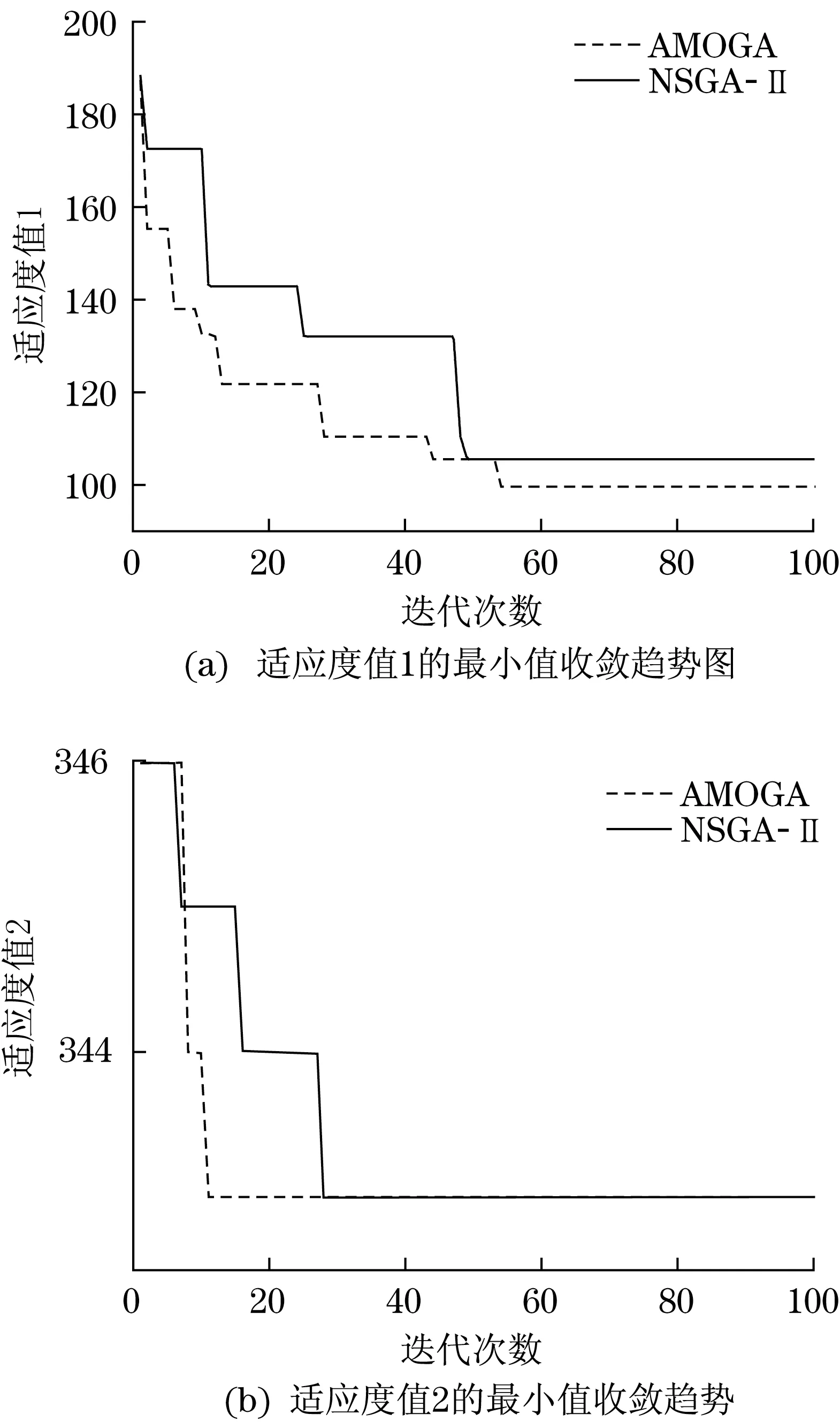
图8 不同算法的适应度值的收敛趋势Fig.8 Convergence of fitness of algorithms

3.3 结果分析

从表4中可以看到，零部件消耗速率波动量最小的是方案1，生产量最大的是方案9，两个目标是互相冲突的，为了提高生产率，需要牺牲零部件消耗速率的波动量。但在表中可发现，如果生产量低于1 151台/d，零部件消耗速率波动量会下降到150以下。即，如果生产率下降0.8%，零部件消耗速率波动会降低56.05%。这个结论对安排生产有指导作用。

表4 托盘数目100个约束下的排序方案Tab.4 Sequencing results under pallet=100

4 结语

本文针对具有固定托盘数量的发动机环形混流装配线排序问题，提出了一种自适应多目标遗传算法和离散事件仿真相结合的多目标排序方法。通过对算法引入自适应变异调整策略，克服了传统算法结果容易陷入局部最优的问题，提高了算法的寻优能力，改善了解的质量。该方法克服了纯解析模型不能考虑固定托盘数目约束的建模难点，能指导企业更好制定环形混流生产线的投产排序问题。