基于自适应控制器的电动汽车电机驱动速度控制研究

王婧婧，陈 清

（1.吉林铁道职业技术学院机械工程学院，吉林吉林132200；2.四川交通职业技术学院汽车工程系，四川成都611130）

近年来，由于环境问题和能源需求的日益增长，电动汽车在解决与环境、能源和健康有关的问题上，逐渐受到消费者和各制造商的关注［1-2］。电机作为电动汽车的驱动元件，其直接影响电动汽车的调速范围和扭矩输出范围。与直流电动机或同步电动机相比，感应电动机驱动器由于其更坚固、紧凑、廉价和可靠的特点，成为电动汽车驱动元件的首选［3］。对于电动汽车的控制通常采用矢量控制或磁场定向控制，一般采用数字轴位编码器和轴上安装的轨迹发生器来检测转子转速［4］。磁通和速度传感器导致驱动系统的尺寸增加，增加了传感器的成本，同时降低了机械鲁棒性及系统的可靠性。无传感器矢量控制［5］作为一种新的技术，可降低驱动系统的成本、体积、硬件复杂度，提高可靠性和噪声抗干扰能力，是一种理想的电动汽车电机控制策略。近年来，研究人员提出了许多改进的速度估计技术［6-8］，如滑模观测器［8］、扩展卡尔曼滤波器、速度自适应磁链观测器和模型参考自适应控制器。在所有的策略中，基于模型参考自适应控制的技术被证明是研究人员提出的最好的方法之一，因为它的公式简单，计算复杂度低，易于实现［9］。

提高电机工作效率可显著提升电动汽车的行驶里程，感应电机磁通损耗对其效率有显著影响，对于恒速运行，若转矩可变，则必须改变磁通，以提高驱动效率。简单状态控制［10］、搜索控制［11］和基于损失模型控制［12］的电机能量优化策略被广泛研究。其中，搜索控制器与其他控制策略相比具有明显的优势，它通过试验和误差方法优化一个重要参数，不依赖于电机或变流器的参数。然而，该方法存在转矩脉动和收敛速度慢的问题，且需要知道最小搜索过程中的评估数。在本文中，采用黄金分割算法可非常快速地收敛算法搜索转子磁链参考值的最优值，将驱动损耗降到最小，完全消除了搜索算法的缺点，提高电机的工作效率。

针对上述分析，本文提出了一种新的基于电阻模型参考自适应速度控制（R-MRAC），利用参考模型自动估计电机转速，为提高电机效率，提出一种基于驱动功率损耗和转速误差信号的能量优化算法。对R-MRAC进行了稳定性分析，证明了所提出控制器在低速和再生制动运行下的稳定性。最后，对不同运动模式进行了仿真，并开展了试验验证。结果表明：采用本文所提出的控制器可实现无速度传感器下电动汽车转速的精确控制，且能够降低系统的功率损耗，提高工作效率。

1 数学模型建立

1.1 基于电阻模型参考自适应控制（R-MRAC）模型

为获得电动汽车转速的控制，采用电阻误差作为参考模型。首先，建立同步旋转坐标系中的定子电压公式：

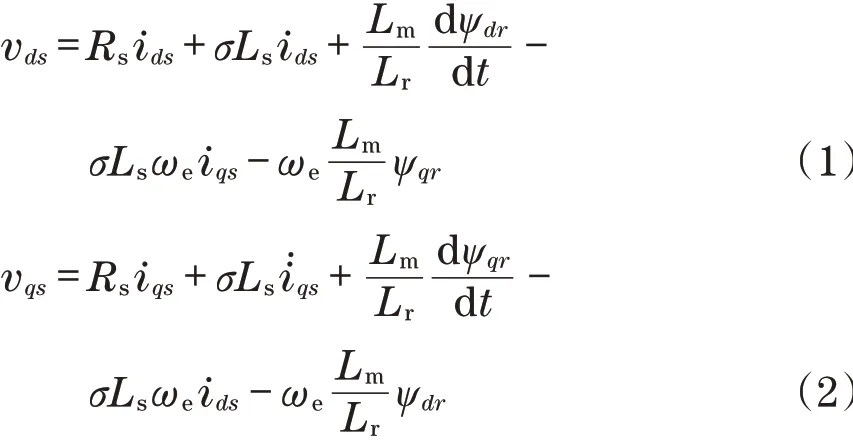
式中：vds、vqs分别为定子电压d轴和q轴分量；ids、iqs分别为定子电流d轴和q轴分量；Ls、Lr和Lm分别为定子绕组、转子绕组和定转子间的互感系数；Rs为定子电阻；σ=1-L2m/(LrLs)为总泄漏系数；ψdr和ψqr分别为转子磁链d轴和q轴分量；ωe为同步速度。

将式（1）除以ids，式（2）除以iqs后，得到RMRAC参考模型方程：

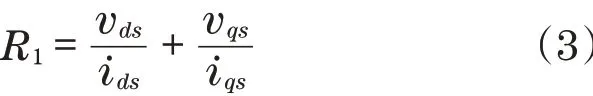
式中：R1为电阻，被定义为虚构的阻抗，可看作为d轴和q轴电阻之间的差。由于R1与转子转速无关，因此被应用于参考模型中。

联立式（1）～式（3），可以获得自适应模型中电阻R1瞬时值的新表达式：

式中：p为求导。

在稳态过程中，当导数项消失时，表达式变为

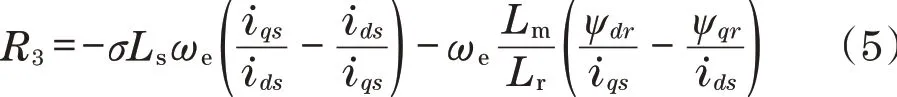
此外，对于矢量控制有ψdr=Lmids和ψqr=0。因此，可以将式（5）简化为与转子磁链无关的表达式：

用式（6）中的σ值代替R-MRAC的自适应模型，可以得到修正的R-MRAC模型表达式：

基于上述公式，可获得用于转速估计的RMRAC结构，如图1所示。包含参考模型和自适应模型，其中分母中的d-q电流分量中添加了一个较小值λ=0.000 01，可确保模型参考自适应控制在空载条件下依然能正常工作。

图1 用于转子转速估计的R-MRAC结构Fig.1 R-MRAC structure for rotor speed estimation

1.2 感应电机矢量控制能量优化模型

为了获得电机良好的动态特性和提高电机效率，将黄金分割算法的效率优化方案引入到感应电机控制的外环中。通过d轴（产生磁链）、q轴（产生转矩）电流控制实现转矩和磁通的解耦控制，简化能量优化算法，所建立的基于R-MRAC的感应电机矢量控制能量优化模型如图2所示。

图2 基于R-MRAC的感应电机矢量控制能量优化模型Fig.2 Energy optimization model of induction motor vector control based on R-MRAC

采用黄金分割效率优化算法生成参考磁通电流i*ds，电流转矩分量则由速度控制回路获得。在瞬态状态下，当速度命令或负载转矩发生变化时，i*ds的标称值发挥作用。当速度误差信号（Δωe）达到最大值0.5 rad/s时，黄金分割能量优化算法确定i*ds为所需的最优电流值，i*ds的最优值在不影响输出功率的情况下生成所需的最佳磁通。磁通的最优值降低了驱动系统的功率损耗，提高了感应电机效率。

1.3 感应电机模型

结合R-MRAC和能量优化模型，以感应电机为控制对象，在d-q坐标框架下，建立其数学模型：

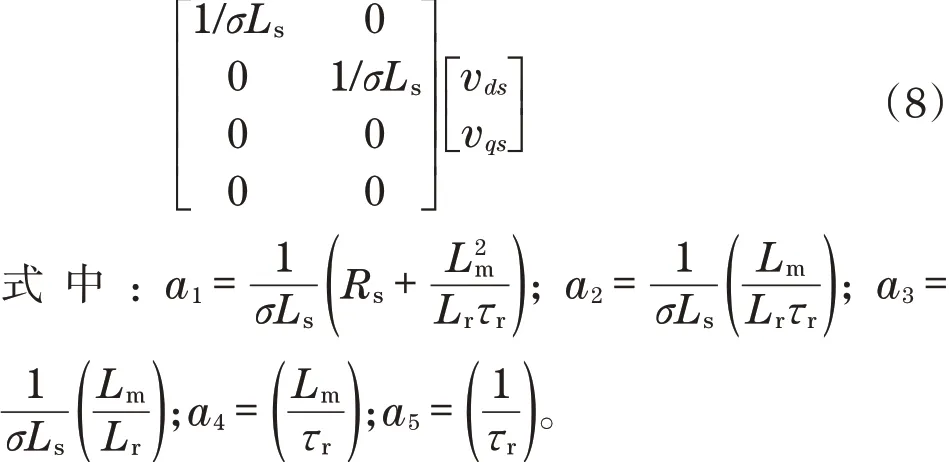
为便于分析，将电机控制矩阵在状态空间中表示如下：

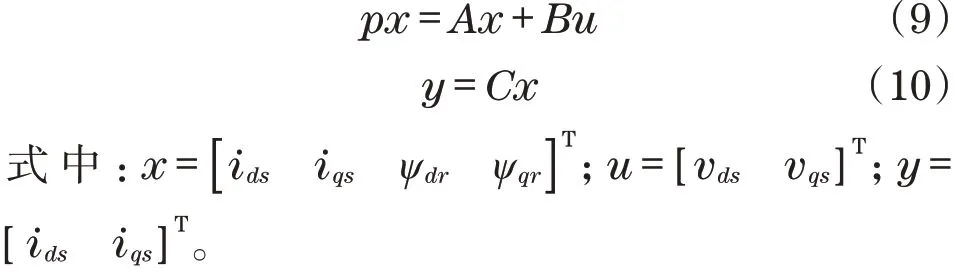
2 系统稳定性分析

针对所提出的电动汽车控制模型，需要对系统进行稳定性分析，以保证系统能够正常运行。本文采用矩阵特征值的方法，分析系统在低速运动和再生制动模式下的稳定性，所研究的感应电机参数如表1所示。

表1 感应电机和控制器参数Tab.1 Induction motor and controller parameters

由于感应电机控制系统矩阵特征值对扰动很敏感，矩阵元素的微小变化可导致特征值发生较大变化。

设矩阵A受到的扰动为P（P=eB，e＞0，B为任意矩阵），特征值λi、右特征向量φi受到的扰动分别用Δλi和Δφi表示，则受扰动下的矩阵A可表示为

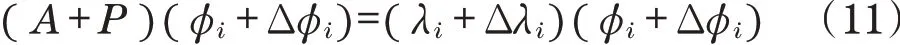
右特征向量φi受到的扰动Δφi可看作是除自身以外的其他右特征向量的线性组合，表示为

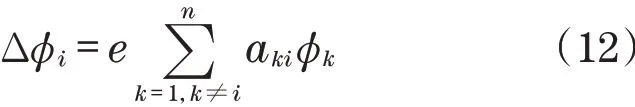
扰动φi中的一阶项可表示为

从状态转移矩阵（2）计算特征值，当ωr=10 rad/s、负载扭矩TL=10 N·m时，在不同定子和转子电阻下，使用R-MRAC控制，用状态矩阵观测两个任意扰动矩阵的特征值，获得复频率平面内特征值分布，如图3所示。

图3 低速运行下系统特征值复平面图Fig.3 Complex plane diagram of system eigenvalues under low speed operation

从图3可以看出，在任意扰动作用下，随着定子电阻和转子电阻的增加，感应电机所有的特征值均位于S平面左侧，证明了所提出的控制系统在低速运行下的稳定性。

同样，当ωr=10 rad/s、负载扭矩TL=-10 N·m时，在不同定子和转子电阻下，使用R-MRAC控制，用状态矩阵观测两个任意扰动矩阵的特征值，获得复频率平面内再生制动模式下特征值分布，如图4所示。

从图4可以看出，在再生制动过程中，任意扰动作用下，随着定子电阻和转子电阻的增加，感应电机所有的特征值均位于S平面左侧，证明了所提出的控制系统在再生制动运动下的稳定性。

因此，可知对于任意的工作模式，所提出R-MRAC感应电机控制均是稳定的。

图4 再生制动运行下系统特征值复平面图Fig.4 Complex plan of system characteristic value under regenerative braking operation

3 实验结果分析

为了验证了所提出的R-MRAC无速度传感器矢量控制系统的性能，在Matlab/Simulink环境下对感应电机进行了不同速度运行和再生制动运行轨迹的跟踪仿真，并开展了加速和减速过程的试验研究。

3.1 不同速度运行

通过参考速度的阶跃变化来研究R-MRAC驱动效果的性能。设定负载扭矩为10 N·m，每10 s施加一次递增的阶跃速度信号，其中，前5 s内不启动能量优化算法，获得整个速度范围内的感应电机速度变化、速度误差和总磁通泄漏变化，如图5所示。

从图5（a）可以看出，随着速度的增加，估计速度始终很好地跟踪参考速度，在0 rad/s上下波动，证明所提出的无速度传感器估计算法能很好地估计参考速度。实际速度与估计速度存在一定偏差，但误差大小始终控制在1 rad/s内，且随着转速的提高，估计速度误差逐渐减小。这是因为在较低的转速下，反电动势较小，但角度误差相对较小，对电机性能影响较小。

图5 不同速度下仿真结果Fig.5 Simulation results at different speeds

此外，可以看出在阶跃变化后5 s内，加入能量优化算法，实际速度误差进一步减小，这是因为黄金分割能量优化算法能快速地将ids调整到最优值。

从图5（b）可以看出，随着速度的增加，电动汽车的总磁通泄漏逐渐减小，与速度变化成反比，在加入能量优化算法后，总磁通泄漏明显减小，进一步证明了所提出能量优化算法的有效性。

3.2 不同转矩影响

为研究转矩的影响，以恒定最低转速10 rad/s和最高转速160 rad/s为参考转速，在5 s时，使负载转矩由10 N·m增加到15 N·m，在15 s时，使负载转矩由15 N·m增加到20 N·m，获得不同转矩下速度变化，如图6所示。

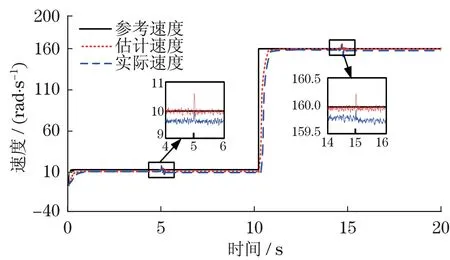
图6 不同转矩下仿真结果Fig.6 Simulation results under different torques

从图中可以看出，无论在较低转速10 rad/s还是较高转速160 rad/s下，转矩突变过程中，电机转速在短时间内发生较大变化，之后迅速减小。整个运行过程中，转速误差均控制在1 rad/s内，表明所提出的矢量控制具有良好的性能。

3.3 再生制动运行

在再生制动模式下，系统参考速度为10 rad/s，恒定负载扭矩为10 N·m。在5 s时刻，给定参考速度阶跃降低到-10 rad/s，获得电机速度变化和扭矩变化如图8所示。

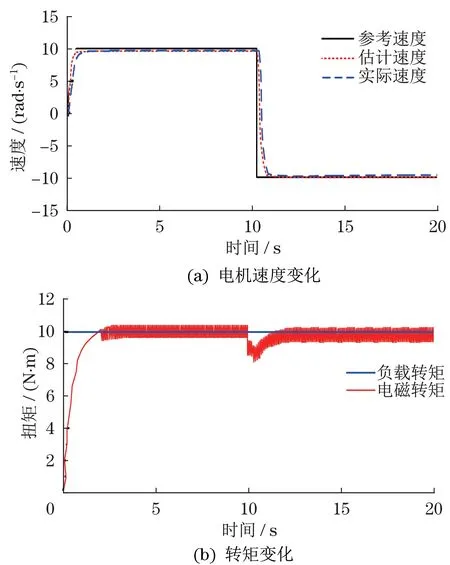
图7 再生制动模式下仿真结果Fig.7 Simulation results under regenerative braking mode

从图7（a）可以看出，在再生制动运行模式下，估计速度始终跟踪参考速度，且实际速度始终跟踪估计速度，施加的负载扭矩和电磁转矩变化如图7（b）所示。在速度突变时刻（10 s），电磁转矩迅速响应，保证了速度跟踪的快速性和精确性。

3.4 试验验证

为验证仿真过程正确性，采用相同的参数，对加速、匀速和减速过程进行了试验研究，并与仿真结果进行对比分析，如图8所示。

可以看出，采用相同的仿真和试验参数，试验结果与仿真结果基本一致，电机速度很好地跟踪参考速度的变化，仿真与试验结果误差不超过5%，表明了本文提出的控制方法的正确性。

图8 不同转速下试验结果Fig.8 Test results at different speeds

4 结论

针对电动汽车速度控制需要安装传感器，以及精度低、成本高的问题，提出了一种基于d-q轴电阻误差的模型参考自适应模型（R-MRAC），主要结论如下：

（1）引入黄金分割能量优化算法，可根据负载变化自动生成最优i*ds值，保证磁通损耗最小。

（2）通过一阶特征值灵敏度分析证明了系统的闭环稳定性，该方案不受定子电阻变化的影响。MRAC的独特形式完全消除了速度估计过程中对任何流量估计的要求。

（3）研究了不同速度、不同转矩和再生制动下的性能，仿真和试验结果表明，采用本文所提出的控制器，可实现无速度传感器下电动汽车转速的精确控制，且能够降低系统的功率损耗，提高工作效率。