起重机设计规范中双向压弯构件验算公式的对比研究

张宏生，陆念力

（哈尔滨工业大学机电工程学院，黑龙江哈尔滨150001）

双向压弯构件是钢结构稳定理论中的一个具有普遍意义的问题，而起重机钢结构主要承受动载荷，结构受力和变形都控制在弹性范围内，理论上不做塑性分析。文献［1］在国内较早开展起重机钢结构双向构件稳定性计算研究，其研究成果被应用于我国首部起重机设计规范［2］（GB 3811—83）和塔式起重机设计规范［3］（GB/T 13752—92）。对于空间双向压弯构件的非线性强度计算，其本质上是构件截面边缘纤维发生屈服。为了验算双向压弯构件的非线性强度，起重机设计规范（GB 3811—83）中非线性强度计算公式（25）考虑轴向压力、空间双向弯矩、初始缺陷、弯矩放大系数等因素的影响，其表达形式为

式中：φψ为主要考虑初始缺陷的影响并利用当量初挠度进行表达的放大系数；Cmy为绕强轴的端部弯矩对绕弱轴端部弯矩的影响系数；Mox、Moy为绕x轴和绕y轴的端部最大弯矩；MHx、MHy为绕x轴和绕y轴的跨中最大弯矩；Cox、Coy为端部弯矩不等的折减系数；CHx、CHy为横向载荷弯矩系数；Wy、Wx分别为绕x轴和绕y轴的抗弯模量；N为轴向压力；A为横截面积；NEx、NEy分别为x轴和y轴的欧拉临界力。

而在塔式起重机中多采用格构式构件，因此塔式起重机设计规范（GB/T 13752—92）中式（31）去掉了Cmy系数，其表达形式为

起重机设计规范（GB 3811—83）和塔式起重机设计规范（GB/T 13752—92）为我国起重机行业的发展作出了重要的贡献。为了引入国内外科学计算发展过程中涌现出来的新技术和新的设计理念，我国分别与2008和2017年发布这两部规范的修订版，分别是起重机设计规范［4］（GB 3811—2008）和塔式起重机设计规范［5］（GB/T 13752—2017）。起重机设计规范（GB 3811—2008）附录M中公式（M.1）的表达形式为

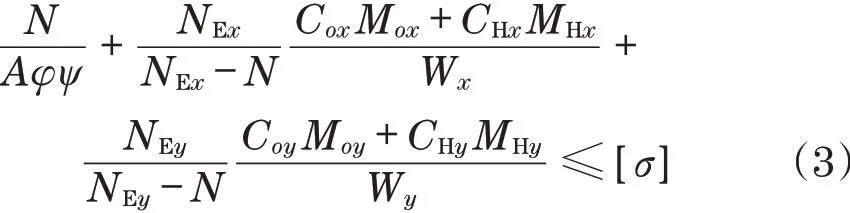
并且附录M中明确提出式（3）是在两个互相垂直的平面内约束条件相同、在弹性工作阶段的等截面构件的前提下推导的。式（3）和式（2）的主要区别是取消了欧拉临界力前的载荷系数0.9，相对而言，式（2）计算得到的复合应力更大，计算结果偏保守。

塔式起重机设计规范（GB/T 13752—2017）中式（54）对以上公式进行了修正，其表达形式为

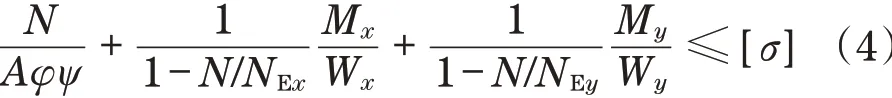
式中：Mx、My为构件计算截面上绕x轴和绕y轴的弯矩。

式（1）～式（3）的推导前提是两个互相垂直的平面内约束条件相同，而且这3个公式对1个构件只验算1次，就是简单将最大的端弯矩和最大的跨中弯矩乘以相应的载荷系数进行简单迭加，公式计算较为简单；式（4）放弃了载荷系数，需要对多个危险截面进行验算，但是规范中并未给出最危险截面位置。

动臂式起重机在国民经济建设中得到广泛应用，其动臂的力学模型如图1所示。起重机动臂在起升平面内可等效为简支梁模型，在起升平面外可等效为悬臂梁模型。本文首先将研究起重机动臂利用式（4）进行验算时的最危险截面位置，然后比较利用式（3）和式（4）进行验算的差异性，最后通过算例进行验证。

图1 典型起重机动臂的力学模型Fig.1 Mechanical model of a typical crane boom

1 起重机动臂载荷分析

假定所研究的起重机动臂为等截面直杆，无初弯曲或初挠度等缺陷，即ψ=1。杆长为l，各截面参数为Ix、Iy、Wx、Wy、A。吊臂与水平面夹角θ，钢丝绳与吊臂根部铰点水平距离为a，垂直距离为b，钢丝绳与吊臂夹角为α。在吊臂根部铰点建立坐标系，z轴沿吊臂轴线方向，x轴垂直起升平面，y轴位于起升平面。可将图1模型等效为悬臂梁模型和简支梁模型。

图2 （a）为悬臂梁模型，图2（b）为简支梁模型。设吊重为P，水平偏摆力为Q，钢丝绳所受拉力为F，吊臂由钢丝绳拉力和吊重P产生的轴力为Na。

由几何关系可以建立α和θ之间的关系，得到

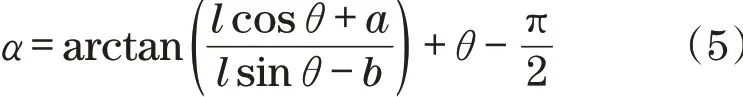
图2 典型起重机动臂的平面内和平面外力学模型Fig.2 In-plane and out-of-plane mechanical model of a typical crane boom

对臂根铰点o点取矩，得到钢丝绳拉力F为

钢丝绳拉力F和吊重P产生轴向压力Na为

塔式起重机设计规范（GB/T 13752—2017）中附录F推荐了受有均布载荷的结构件的折算轴向等效方法，将起重机动臂轴向均布载荷qsinθ等效为杆端集中载荷。同时考虑到起升平面内为简支梁模型，起升平面外为悬臂梁模型，由此得到

起重机动臂平面内和平面外的任意一点弯矩可表示为

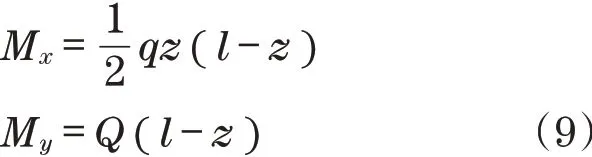
起重机动臂平面内为简支梁模型，平面外为简支梁模型，其欧拉临界力NEx和NEy分别为

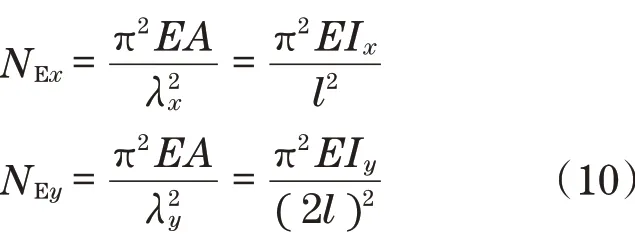
2 非线性强度验算公式

2.1 《起重机设计规范GB/T 3811—2008》验算公式

在本文所研究的起重机动臂模型中（见图1），将载荷Mox=0，Moy=Ql，MHx=ql/4，MHy=0，以及相关的系数分别为Coy=0.6，CHx=1，将各项系数代入式（3），得到常量的应力σ1为

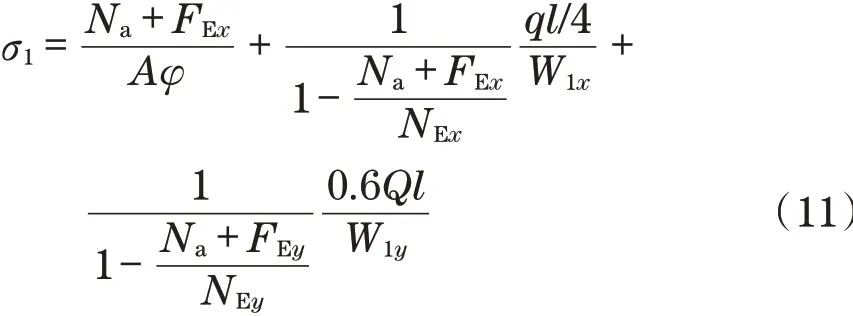
2.2 《塔式起重机设计规范GB/T 13752—2017》验算公式

将各项系数代入式（4），得到跟位置z有关的应力函数σ2(z)为

对式（12）取一阶导数为0，得到应力函数σ2(z)取极大值的最危险截面位置zM为

需要注意的是，在式（13）中，水平偏摆力Q通常为吊重P的函数，由偏摆角β描述，

当偏摆角过大，式（13）中最危险截面位置ZM可能为负值，这时应该取最危险截面位置ZM=0。由式（13）可知，最危险截面位置ZM是吊臂各参数的函数，特别是结构设计完成后，两个重要影响参数为吊臂倾角θ和偏摆角β。

将最危险截面位置ZM代入到应力函数σ2(z)，即可求出构件截面最大应力为

3 算例验证

某动臂式起重机的动臂参数如表1所示，分析该吊臂的危险截面位置，重点研究其与吊臂倾角θ和偏摆角β之间的关系。为了进行无量纲化处理，图3的纵坐标为zM/l，并利用式（11）和式（15）进行校核。

由图3可知：偏摆角β对危险截面位置影响较大，特别是当偏摆角β很小接近于0时，最危险截面接近跨中；而偏摆角β大于某一个角度（本例是2.2°）时，最危险截面位于臂根处。而吊臂倾角θ对吊臂危险截面位置影响很小。

表1 某起重机动臂参数Tab.1 Parameters of a typical crane boom

由图4和图5可知：随着吊臂倾角θ的增大，最大计算应力σ1和σ2都将减小，但是σ1减小的幅度更大；而偏摆角β大于某一个角度（本例是1.1°）时，σ2计算结果比σ1大，σ2计算结果偏保守；而偏摆角β小于某一个角度（本例是1.1°）时，σ1计算结果比σ2大，σ1计算结果偏保守。因此，利用式（11）和式（15）进行双向压弯构件的非线性强度验算，需要根据偏摆角不同进行适当选择。

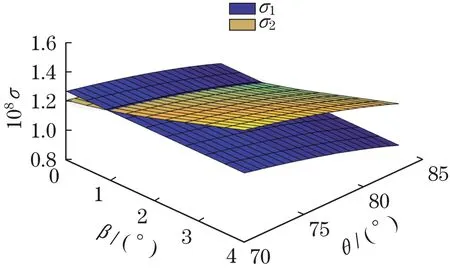
图4 不同规范应力结果和吊臂倾角θ和偏摆角β关系Fig.4 Design rules results with different boom angle θand hoisting skew angleβ

图5 σ1/σ2和吊臂倾角θ和偏摆角β关系Fig.5σ1/σ2 with different boom angleθand hoisting skew angleβ

4 结论

本文回顾了起重机设计规范和塔式起重机设计规范中关于双向压弯构件非线性强度验算公式的发展历程，通过理论分析并结合数值模拟，利用算例展示了双向压弯构件校核问题，得到以下结论：

（1）给出了塔式起重机设计规范（GB/T 13752—2017）进行非线性强度验算的构件危险截面位置公式，当偏摆载荷过大时，危险截面位于吊臂根部。

（2）吊臂倾角θ对吊臂危险截面位置影响很小，偏摆角β对危险截面位置影响较大。

（3）随着吊臂倾角θ的增大，利用起重机设计规范（GB/T 3811—2008）和塔式起重机设计规范（GB/T 13752—2017）得到的非线性强度σ1和σ2都将减小。

（4）偏摆角β的不同，需合理选择起重机设计规范（GB/T 3811—2008）和塔式起重机设计规范（GB/T 13752—2017）中非线性强度验算公式。