三角形周长为定值的内切圆半径最值问题探究*

江苏省南通市天星湖中学(226010) 钱 鹏

在高三数学迎考复习教学中编制微主题式研究性学习单或微专题导学单,从数学杂志或者各地模考题中挖掘题源,进一步整合,从而达到解一题而通一类,是解题教学的目标之一.

题目(2019年12月武汉市模考试题填空压轴题)已知∆ABC的周长为9,若求∆ABC的内切圆半径r的最大值.

探求结论往往明确解题方向.注意到的对称性, 猜想A=B时内切圆半径最大, 此时A=B=C=如图1所示, 有r=ID=

图1

解法1记∆ABC的内角A,B,C的对边为a,b,c,

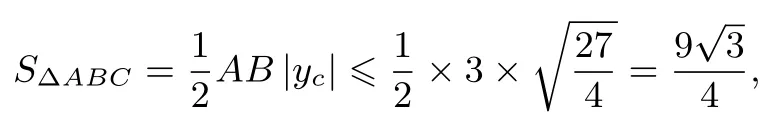
又S∆ABC=(a+b+c)r=故所以∆ABC的内切圆半径的最大值为

解法2由

记∆ABC的内切圆I切边AB,BC,CA于点D,E,F,记AD=DF=x,BD=BE=y,CE=CF=z.

图2

如图2 所示,则x+y+则依题意可知S∆ABC=(a+b+c)r=(x+y+z)r,由海伦公式得S∆ABC=所以r2=结合可得x+y+z= 3z, 又因为x+y+z=所以

注对于还有另一种转化方式.借助于半角公式

以及正弦定理、余弦定理可得

由a+b+c=9,得a+b=6,c=3.

推 广若 ∆ABC的周长为l,=则∆ABC的内切圆半径r的最大值为面积S∆ABC的最大值为

证明由

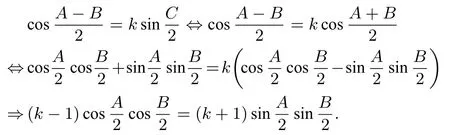
由题意得a+b+c=l,S∆ABC=因为即

在∆ABC中,有三角恒等式所以所以

所以S∆ABC=所以当A=B,∆ABC的内切圆半径r的最大值为面积S∆ABC的最大值为