基于奇异摄动理论的机器人关节控制研究

夏 杭，段现银，闵华松，黄文晖，吴修玉

(1. 武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2.武汉科技大学机器人与智能系统研究院，湖北 武汉，430081；3.武昌首义学院机电与自动化学院,湖北 武汉，430064)

传统工业机器人由于体积大、自重载荷比低和工作环境单一等缺点，越来越不能满足人机共融环境下的要求，而柔性机械臂在工作时表现出良好的顺应性受到行业广泛关注[1]。但柔性关节内部存在具有弹性属性的元器件、谐波减速机等零部件，这些具有弹性属性的零部件让关节控制变得更加困难,且谐波减速机内的非线性摩擦会导致机械臂在运动过程中产生抖动[2]。关节弹性容易导致关节在控制过程中产生残余振动、收敛速度慢，且超调量大[3]，给关节的控制系统设计带来了很大的挑战。研究人员对提高柔性关节控制精度所采取的研究方法主要有奇异摄动法[4]、反馈线性化法[5]、结合关节扭矩反馈的级联系统方法[6]。反馈线性化法是将柔性关节的非线性系统转化为线性系统，但运用该方法需要引入状态观测器，才能保证转化为线性系统时的准确性，因此也增加了控制系统的复杂性；结合关节扭矩反馈的级联系统方法是将机器人系统分为柔性和刚性两个部分，然后直接对刚性部分的动力学进行控制，最后将反馈力矩补偿到柔性部分，但该方法依赖准确采集系统输出力矩和精准的关节动力学模型；奇异摄动法是将柔性关节系统解耦成两个子系统，首先补偿关节柔性部分，再对关节进行控制[7]。

为了抑制关节振动，国内外研究人员展开了系列研究，Petit等[8]提出了基于模型的状态反馈控制器，通过将关节输出信号进行处理后反馈到输入端，从而有效抑制关节振动，但该方法在建模时忽略了关节内部摩擦和外界干扰的影响；Petit等[9]还提出了一种无模型的阻尼控制方法，该方法利用联合弹性将动能转换为弹性能来实现振动抑制；Sun等[10]提出了一种基于在线重力补偿的抑振位置控制方法来有效地减小柔性关节输出角度的超调量；韩吉霞等[11]提出了在控制策略中引入干扰观测器来减小关节振动和保证关节控制的鲁棒性。

由于关节内部摩擦力矩形式复杂且难以估算，目前在对柔性关节控制研究中大多忽略了摩擦力矩对位置控制的影响，但在实际应用中，弹性元器件和谐波减速机的使用带来了关节内部不可忽略的柔性和摩擦以及关节弹性振动等问题。为此，本文针对机器人柔性关节存在位置控制精度低的问题,在考虑关节内部非线性摩擦和外界扰动等因素的情况下，建立柔性关节动力学模型，提出基于奇异摄动理论的干扰观测器滑模控制方法，利用该控制方法对关节控制系统进行Lyapunov稳定性分析和MATLAB仿真，以期为机器人关节控制研究提供参考。

1 柔性关节动力学建模

1.1 柔性关节的构成及控制系统

柔性关节的构成及控制系统如图1所示。从图1(a)中可以看出，柔性关节将无框力矩电机、谐波减速机、霍尔传感器、磁环编码器、弹性元器件、制动器、驱动器等多种零部件集成于一体，该关节具有体积小、输出扭矩大、便于维修等优点，并且具有标准的机械接口和电气接口。在图1(b)中，无框力矩电机为关节提供动力；谐波减速机由于质量轻、减速比大，能进一步提高关节输出扭矩；弹性元器件具有抗冲击性强的特点，将动力传递到关节的法兰；霍尔传感器和磁环编码器采集电机端和关节输出端的位置和速度信息；制动器提供位置保持和电源保护。

(a)关节机械结构图

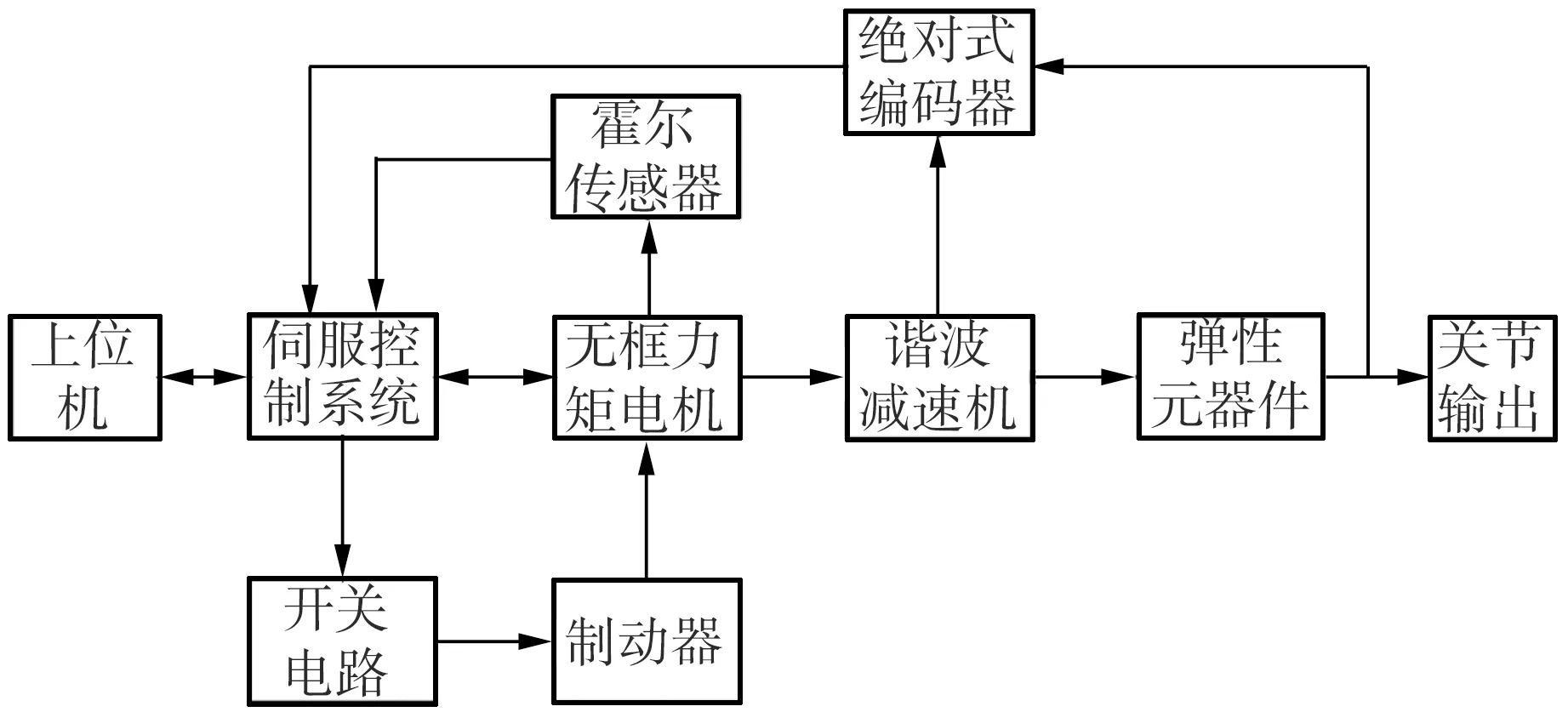
(b)关节控制系统框图

1.2 柔性关节动力学模型

Spong[12]建立了一种最初的柔性关节简化模型，将关节中具有弹性属性的元器件和谐波减速机等零部件等效为弹性系数不变的扭簧，但该模型忽略了关节内部非线性摩擦和外界干扰等因素的影响，不能完整地表示关节内部的物理特性。良好的动力学模型不仅能真实反映关节内部的物理特性，而且是实现关节准确控制的前提。本文在考虑关节内部摩擦和关节外部干扰因素的情况下，对摩擦力进行辨识，并对柔性关节进行动力学建模，其简化模型如图2所示。柔性关节动力学方程为：

(1)

式中，Tm、T、Ta、Tf、Te分别为电机电磁转矩、关节力矩、关节内部摩擦与外界扰动产生的力矩之和、关节内部摩擦力矩、外界扰动力矩，N·m；Jm、Jl分别为电机转动惯量和负载转动惯量，kg·m2；K为柔性扭转弹性系数，N·m/rad；Bl为负载阻尼系数，N·m·s/rad；θm、θl分别为电机转角、关节转角，rad。

图2 柔性关节简化模型

1.3 摩擦力模型与参数辨识

柔性关节内部摩擦属于混合摩擦，单一的摩擦形式无法准确描述柔性关节内部的摩擦情况。Stribeck摩擦模型[13]包含有库伦摩擦和最大静摩擦，能比较全面地描述关节内摩擦特性，其模型为：

(2)

式中,fc、fs分别为关节内部库伦摩擦力矩、最大静摩擦力矩，N·m；ω、ωs分别为关节旋转角速度和Stribeck速度，rad/s；Bv为关节内部黏性摩擦系数，N·m·s/rad。

对于单关节Stribeck摩擦模型的参数辨识，首先设计三阶傅里叶级数作为激励轨迹，激励频率为100 Hz，采样周期为10 s；其次采集关节角度与力矩值，对关节角度差分求取关节角速度，对关节角度二次差分获取关节角加速度，并采用低通滤波对所采集的关节力矩值以及关节角度信号进行滤波；最后用最小二乘法辨识求得关节内部摩擦力模型参数如表1所示。

表1 Stribeck 摩擦模型参数

2 控制器的设计与稳定性分析

由于柔性关节在转动过程中容易产生振动，因此需要设计能同时实现位置跟踪和抑制关节振动的控制器。依据奇异摄动理论，将柔性关节系统解耦为不同时间尺度并且相互独立的两个低阶子系统，然后分别针对两个独立的子系统设计控制器[14]。令:

Tm=us+uf

(3)

式中，uf为快变子系统控制量，N·m；us为慢变子系统控制量，N·m。

(4)

快变子系统控制律为：

(5)

式中，Kv为力矩反馈微分增益系数。

关节力矩方程可表示为：

(6)

令ε=0，得慢变子系统方程为：

(7)

2.1 基于干扰观测器的慢变子系统滑模控制

将式(7)化为标准形式得：

(8)

所设计的滑模面函数(s)为：

(9)

式中，关节位置误差e=θd-θl，其中θd为关节期望位置。

针对慢变子变系统，设计滑模控制律为：

(10)

式中，fd为通过干扰观测器对f项的估计值，N·m；kf为切换增益系数，将其设计为：kf>|fe|，其中，fe为f项的估计误差，N·m,fe=f-fd。

定义李雅普诺夫函数为：

(11)

=-[fd+kfsgn(s)]+f

=fe-kfsgn(s)

(12)

由式(11)和式(12)得：

(13)

由于对f项的估计误差fe足够小，则需要将切换增益系数kf设计成很小的值，从而有效地抑制关节振动。

干扰观测器的设计为：

(14)

2.2 稳定性分析

定义李雅普诺夫函数为：

(15)

对式(15)求导得：

(16)

=-fex1+x1(fe-k2x1)

(17)

3 仿真

关节系统控制框图如图3所示。计算得到关节转动惯量为0.405×10-2kg·m2，负载端转动惯量为0.605×10-2kg·m2，柔性关节刚度为450 N·m/rad，阻尼系数为0.05 N·m·s/rad，外界扰动力矩Te取2sintN·m，干扰观测器中的极点增益参数k1=2300、k2=320，切换增益系数kf=3。分别对柔性关节进行定位和位置跟踪仿真试验，关节转动的期望位置分别为5 rad和5sin(2πt)。关节输入为阶跃信号下的响应如图4所示，关节输入为正弦信号下的响应如图5所示。从图4中可以看出，在进行关节位置保持仿真时，关节系统上升时间为0.107 s，在经过0.217 s后进入稳定状态，关节转动5 rad后速度快速降低到0，并且稳态误差趋近于0，由此表明，该关节系统调节时间短、稳态误差小、定位精度高。从图5中可以看出，在进行关节位置跟踪仿真时，关节位置跟踪响应时间为0.109 s，经过0.109 s后，关节输出角度与关节期望角度(5sin(2πt))接近，关节位置误差在-0.176～0.152 rad范围内波动，表明关节位置跟踪误差较小，且跟踪响应速度较快。由此可见，本文提出的基于奇异摄动理论的干扰观测器滑模控制方法能够有效减小关节内部摩擦和外界干扰对关节控制精度的影响。

图3 关节系统控制框图

(a)关节输出角度

(b)关节输出角速度

(a)关节输出角度

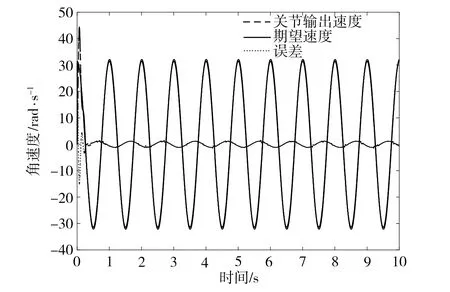
(b)关节输出角速度

PD控制下关节定位仿真结果、无干扰观测器关节定位仿真结果分别如图6和图7所示，关节定位误差量化对比如表2所示。对比图4、图6、图7以及表2可以看出，在PD控制和无干扰观测器控制下，关节系统超调量和稳态误差过大，采用干扰观测器滑模控制方法后，关节系统超调量降低至15.78%，关节系统稳态误差降低至0.028 rad。由此可得，在有摩擦和外界干扰的影响下，PD控制方法无法实现关节输出保持稳定，超调量大，有明显的振动；在引入干扰观测器后，基于奇异摄动理论的干扰观测器滑模控制方法能够使关节输出响应速度加快，系统在经过0.217 s调节后达到稳定状态，稳态误差减小到0.028 rad,系统的控制精度明显提高。

图6 PD控制下关节定位仿真结果

图7 无干扰观测器关节定位仿真结果

表2 不同控制方法下关节定位误差量化对比

PD控制关节位置跟踪仿真结果、无干扰观测器关节位置跟踪仿真结果分别如图8和图9所示，关节位置跟踪误差对比如图10所示，不同控制方法下关节位置跟踪误差量化对比如表3所示。由图8、图9和图10以及表3可以看出，在PD控制和无干扰观测器控制下，关节位置跟踪误差范围比较大，跟踪响应时间也较长；在引入干扰观测器后，跟踪误差范围缩小为-0.176～0.152 rad，跟踪响应时间缩短至0.109s。由此可见，基于奇异摄动理论的干扰观测器滑模控制方法可以减小关节由内部摩擦和外界干扰引起的位置跟踪误差，跟踪响应速度更快，跟踪性能更好。

图8 PD控制关节位置跟踪仿真结果

图9 无干扰观测器关节位置跟踪仿真结果

图10 关节位置跟踪误差对比

表3 不同控制方法下关节位置跟踪误差量化对比

4 结语

(1)针对机器人柔性关节控制精度低的问题，提出了一种基于奇异摄动理论的干扰观测器滑模控制方法,该方法在引入干扰观测器后，可以减小关节内部非线性摩擦和外界干扰对关节控制精度的影响。

(2)与PD控制方法和无干扰观测器控制方法相比，所提出的基于奇异摄动理论的干扰观测器滑模控制方法能够缩短关节控制系统调节时间，且超调量低，能有效抑制关节振动和提高系统的控制精度。