基于摩擦轮反馈的数字液压缸系统

赵明安，詹江正，刘 忠，霍佳波，石世杰

(1.桂林航天工业学院 机械工程学院，广西 桂林 541004；2.深圳光启高等理工研究院，广东 深圳 518057)

引言

液压技术广泛应用于工业中，但传统液压技术逐渐不能满足工业需求，仅能通过多种控制阀来控制液压缸的载荷与速度，却无法满足准确的载荷要求，过大载荷造成零件损坏，过小载荷无法满足要求[1-2]。根据工程实际需求，数字液压更加具备竞争力，成为当前发展趋势，在航天、汽车和冶金等方面得到广泛应用[3-5]。

由于对称阀控非对称缸的工作性能不相同，因此在建模分析非对称缸时，需区别于对称缸[6-7]。李洪人[8]和马立峰[9]分别对比对称阀与非对称阀控制非对称缸的性能，证明非对称阀控非对称缸的性能更优越，但是由于非对称液压阀产品较少，而非对称液压缸结构简单紧凑，制造简便，性能可靠，工作空间较小，因此工程上偏向于研究对称液压阀控制非对称液压缸[10-11]。然而目前诸多数字液压缸的研究中，仍存在一些问题，如专利201710771383.6公开一种阀套可随动的数字液压缸[12]，采用阀芯和阀套调节阀口，中空活塞杆和滚珠丝杠构成内反馈系统，而丝杆浸润油液中，伴随机械磨损会加剧油液污染，影响反馈精度；可随动滑套也会增加制造难度，减低密封性；且中空活塞杆强度大大降低，安全性降低。邢继峰等[13]提出一种新型数字液压缸，活塞缸伸缩位移通过齿轮齿条，传递至反馈螺母，使阀芯移动复位，从而达到反馈的目的。然而，齿轮齿条结构并不适用于长行程的液压缸，且齿条随活塞杆伸缩，会存在干涉影响。

基于上述问题，提出一种摩擦轮柔性闭环反馈式数字液压缸，利用活塞杆移动增量，通过摩擦轮反馈装置，调节滑阀开口，控制流量，从而对液压缸载荷大小和速度进行精确控制，其反馈机构简单，采用外部柔性闭环位置反馈连接，可减少构件磨损，可靠性高。首先按照三维模型传递结构建立了数字液压缸整体理论数学模型；再根据数学模型建立了MATLAB/Simulink系统仿真框图，按照相关参数，对数字液压缸理论模型进行模拟论证；最后利用AMESim仿真软件对液压系统进行建模仿真，通过实验仿真结果，对液压缸液压系统的性能进行研究分析。

1 结构方案及工作原理

摩擦轮反馈式数字液压缸，包括缸体、活塞杆、驱动电机、滑阀、连接支架和摩擦轮反馈装置。活塞杆外端连接负载，且与摩擦轮形成摩擦传动；电机驱动轴连接滑套；阀芯一端设置花键，与滑套内花键槽形成花键配合；阀芯另一端有螺纹结构，与反馈螺母形成螺纹连接；摩擦轮反馈装置包括摩擦轮、锥齿轮和涡轮蜗杆，通过支架安装于缸体前端，2个摩擦轮设置于活塞杆双侧，转动轴贯穿摩擦轮安装于支架上，且转动轴上端分别有同步啮合的锥齿轮，与之配对的齿轮副连接于蜗杆结构，涡轮连接反馈螺母，且限制螺母轴向移动，仅能绕轴线旋转，其结构图如图1所示。

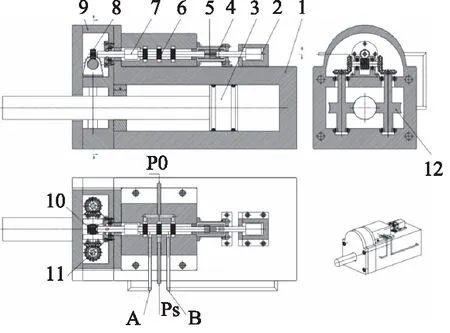
1.缸体 2.步进电机 3.活塞杆 4.滑套 5.花键配合 6.阀芯 7.反馈螺母 8.涡轮 9.支架 10.蜗杆 11.锥齿轮 12.摩擦轮

数字液压缸负向回缩工作原理：步进电机2正向转动，输出扭矩，带动滑套4转动，滑套4内的花键槽5套合阀芯6右端花键，带动阀芯6转动，且阀芯左端螺纹配合旋入反馈螺母7，带阀芯6向左移动，进油口打开，高压油经过A油口进入有杆腔，活塞杆3收缩移动。缸体外部活塞杆带动两侧摩擦轮12转动，经过锥齿轮11啮合，传递至蜗杆10，再经过涡轮蜗杆配合，带动与涡轮连接的反馈螺母7反转，通过阀芯螺杆和反馈螺母旋出运动，使阀芯6向右移动，将阀口关闭，从而达到反馈控制。同理，正向伸出的工作原理则相反，其数字液压缸的控制流程图如图2所示。

图2 控制流程图

2 阀控非对称缸液压系统建模

为了方便对数字缸传动进行研究，对反馈传动结构进行理想化假设：

(1)滑套花键槽与阀芯花键间隙配合精度足够高；

(2)阀芯螺杆与反馈螺母的螺纹配合精度足够高；

(3)涡轮蜗杆传动配合精度足够高；

(4)锥齿轮制造精度足够高，且同步传动；

(5)摩擦轮同步与活塞杆摩擦传动，没有产生滑动情况。

2.1 输入环节方程的建立

摩擦轮反馈式数字液压缸输入环节采用步进电机，通过外部信号驱动步进电机，输出角位移。假设理想情况下，步进电机正常工作，并且不产生失步情况，则步进电机角位移与脉冲数的关系：

θ1=θ·N

(1)

式中,θ1—— 步进电机旋转角位移

θ—— 步进电机步距角

N—— 步进电机脉冲数

2.2 阀芯移动方程的建立

在反馈螺母螺纹副作用下，阀芯沿轴线移动，其移动量可以表示为：

(2)

式中,t—— 阀芯螺杆导程

θ1—— 步进电机输出转角

θ2—— 反馈螺母转角

2.3 液压滑阀数学模型的建立

根据理论分析结果，简化相关理论模型，忽略部分次要影响因素，以分析主要影响因素[14-16]。提出部分假设如下：

(1)液压介质压缩性极小，甚至不可压缩，静态时密度变化很小，可以忽略；

(2)液压油的密度、温度和弹性模量恒定为常数；油源处于理想状态，其压力恒定为常数，回油压力为0，不产生压力冲击和压力饱和现象；

(3)工作腔容积为常数；

(4)缸体内泄漏为层流流动；

(5)滑阀是理想的：即阀开口形式为绝对零开口，且制造精度足够高，几何尺寸绝对正确，不会产生泄漏。

当数字缸正向运动时，即活塞杆向外伸出，xv≥0，则滑阀的压力-流量方程表示为：

(3)

(4)

当数字缸负向运动时，即活塞杆向内收缩，即xv≤0，则滑阀的压力-流量方程表示为：

(5)

(6)

为了方便Simulink理论模型搭建，对流量方程进行整理变换：

(7)

(8)

式中,Cd—— 滑阀流量系数

ω—— 阀芯面积梯度

ρ—— 油液密度

p1—— 无杆腔工作压力

p2—— 有杆腔工作压力

ps—— 油源压力

p0—— 回油压力

2.4 液压缸流量连续性方程的建立

在实际工程中，建立数字缸流量连续性方程相对困难，因此，忽略部分次要因素，对数字缸进行简化讨论，假设：

(1)缸体外部承受标准大气压，且忽略外泄漏；

(2)连接的液压管道对称且短而粗，忽略其中压力损失和外泄漏；

(3)腔体内油液的弹性模量和温度恒定为常数；

(4)忽略腔体内的层流流动；

(5)液压缸外泄漏系数为0。

(9)

(10)

式中，A1—— 无杆腔活塞面积

A2—— 有杆腔活塞面积

Cip—— 内部泄漏系数

Be—— 油液的有效体积弹性模数

V1—— 无杆腔容积

V1=V01+A1xp

式中，V01—— 无杆腔初始容积

V2—— 有杆腔容积

V2=V02-A2xp

式中，V02为有杆腔初始容积。

2.5 力平衡方程的建立

高压油经过液压阀进入液压缸工作腔，在压力的作用下，液压缸活塞进行移动，由活塞杆输出拉力或者推力。根据数字液压缸工作情况，建立相关的力平衡方程。

(11)

式中,m—— 折算至活塞和外负载的等效总质量

BP—— 活塞和负载的黏性阻尼系数

F—— 外负载作用力

2.6 反馈环节数学模型的建立

由液压缸外传动链形成闭环反馈结构，活塞杆位移增量转化为旋转运动，经过摩擦轮、锥齿轮和涡轮蜗杆传动链，传递至反馈螺母，其反馈转角可以表示为：

(12)

式中,xp—— 活塞杆移动量

I总—— 锥齿轮和涡轮蜗杆的总传动比

R—— 摩擦轮最小半径

3 基于Simulink的理论分析

根据所推导建立的理论数学模型，利用Simulink建立液压系统仿真框图，如图3所示。阀控液压缸高频工作，可以将活塞处于限制行程的中间位置，忽略活塞杆位置对液压缸工作性能的影响。

图3 仿真框图

根据数字液压缸相关领域的文献资料，初步拟定仿真参数，其部分具体参数如表1所示。

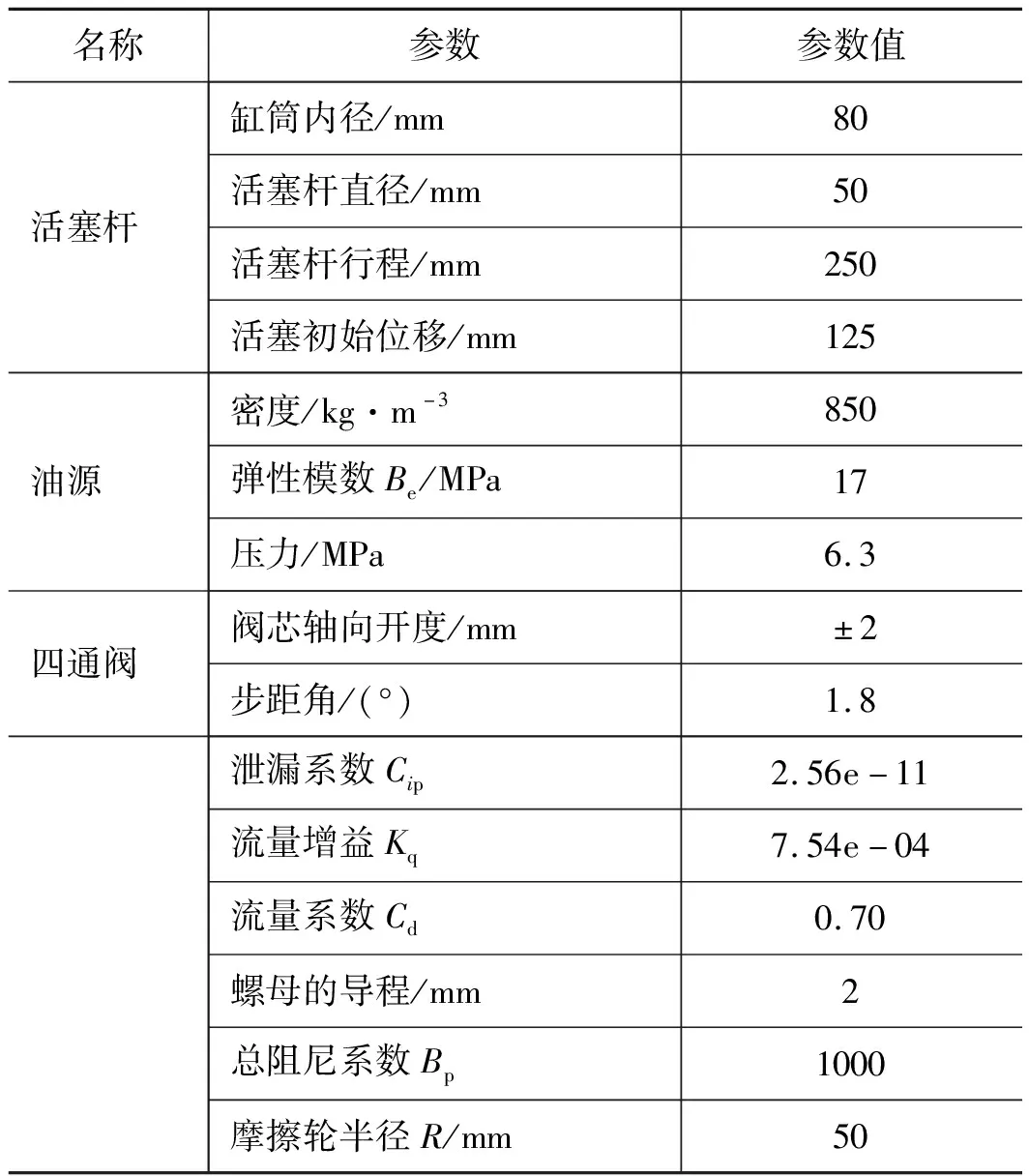
表1 仿真参数表

(1)在液压活塞杆不添加外部负载的情况下，设定液压系统相应的输入信号，设定仿真时间为20 s，得到输入信号与液压缸位移曲线，其电机信号、阀芯位移和活塞杆位移对比曲线如图4所示。

图4 运动情况对比曲线图

由图4可以看出，按照设定输入信号，步进电机开始运作，液压滑阀阀口被打开，油液进入腔体内，活塞杆伸出1 s时，阀芯开口最大；5 s时，液压缸活塞杆开始回缩至行程中间位置；11 s时，活塞杆回缩至负向限制位移。信号回零，活塞杆也回至初始行程中间位置。

步进电机输入转角与反馈螺母反馈角对比曲线如图5所示。步进电机输入转角与反馈螺母的反馈角基本相合，在数字液压缸反馈机制中，能够反应出闭环反馈的原理。

图5 输入转角与反馈转角对比曲线图

(2)在液压活塞杆不添加外部负载的情况下，设定液压系统的信号为正弦信号，频率分别设置为：1.0, 0.8，0.5 rad/s，运行仿真，得到阀芯位移和液压缸位移曲线，如图6所示。

图6 不同频率的阀芯和液压缸位移曲线图

改变外部信号输入状态为正弦曲线，阀芯位移也呈正弦形式，因此，液压缸活塞杆位移随着阀芯正弦式移动而呈现正弦位移。随着频率的减小，阀芯位移周期增大，且位移振幅随之减小。这是由于阀芯正弦周期增大，阀芯开口变小，而油液供油压力不变，液压缸活塞杆位移周期随之增大。

4 基于AMESim建模仿真分析

4.1 AMESim模型建立

为了AMESim模型建立，采用齿轮齿条模型代替摩擦轮的摩擦传动，采用减速机模型代替锥齿轮和涡轮蜗杆总传动比[17-19]。根据摩擦轮反馈式数字液压系统结构和反馈原理，对各个环节进行联立，建立整体数字缸模型，其模型如图7所示。此数字液压缸模型从结构和反馈原理上基本考虑到摩擦轮反馈式数字液压缸的组成。

图7 整体模型图

4.2 AMESim仿真分析

按照表2的仿真参数，设置相应元件子模型、相关参数和边界条件。

表2 AMESim仿真参数表

运行AMESim仿真。其电机信号、阀芯位移和活塞杆位移对比曲线如图8所示。

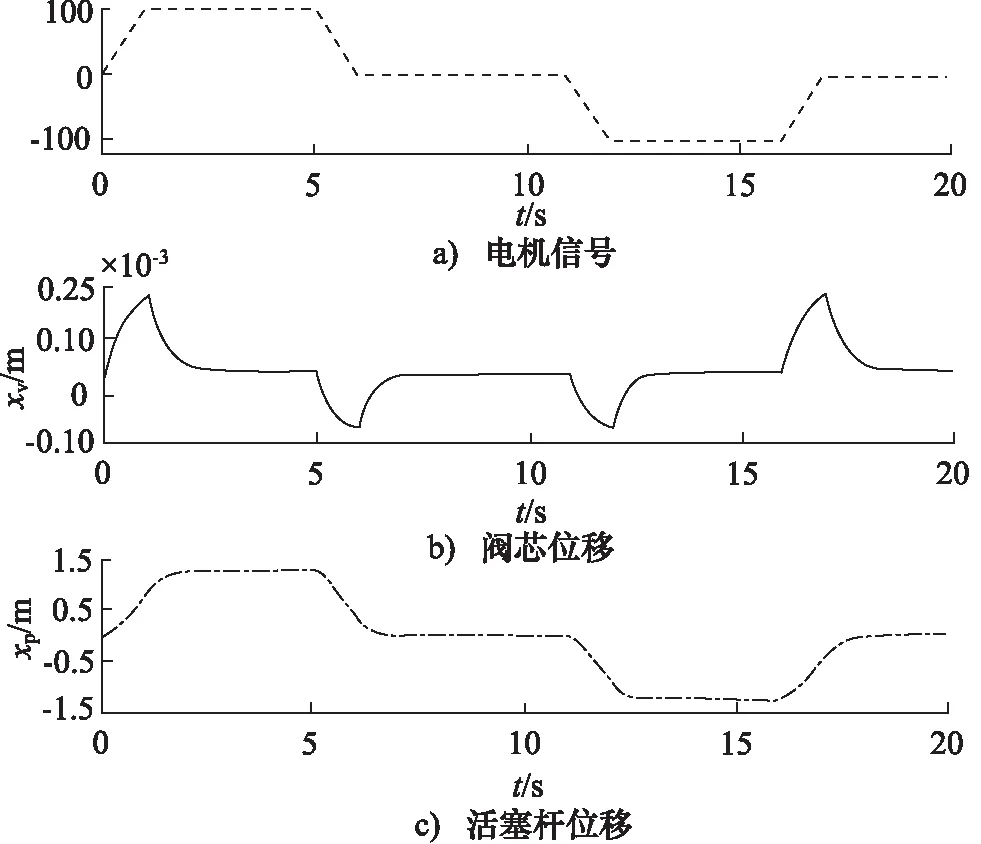
图8 运动情况对比图

由图8可知，在1 s左右，阀口开度最大，随后逐渐缩小，阀芯随反馈螺母反馈机制，被推回零位置；在4 s左右，信号反向，阀口负方向打开，液压缸退回初始的中间位置处；11 s时，信号负反向，阀芯液压缸活塞杆回缩至限制位移处；16 s时，信号正向至零位，液压缸输出至中间位置。

对比图4和图8可知，AMESim仿真曲线与Simulink仿真曲线基本一致，输入信号、阀芯位移和液压缸位移的运动情况和相应状态均能相互对应，且符合实际数字液压缸的反馈运动，因此，AMESim模型建立合适，仿真结果相对准确。步进电机输入转角和反馈螺母的反馈转角对比曲线如图9所示。

图9 输入转角与反馈角对比图(AMESim仿真)

对比图5和图9可知，AMESim仿真结果与Simulink仿真结果基本一致，步进电机输入转角与反馈螺母的反馈角基本相合，能够反应出闭环反馈的原理。输入信号与液压缸位移对比曲线如图10所示。液压缸位移随着输入信号的轨迹而改变，从走向形式上，输入信号能够反映出液压缸位移。

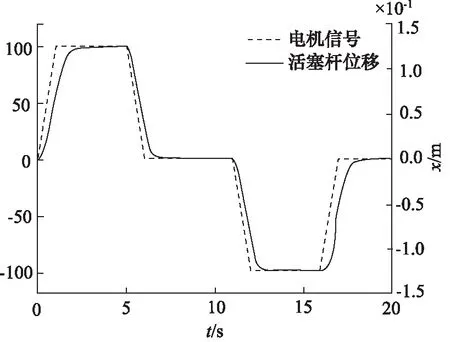
图10 输入信号与液压缸位移对比图

5 结论

提出一种柔性闭环反馈式数字液压缸系统，并建立了相关的数学函数模型，通过Simulink和AMESim仿真软件进行建模仿真分析，并对比其仿真结果，验证数学模型和AMESim模型的正确性及系统方案的可行性。这两个软件都很直观方便地反应了柔性闭环反馈式数字液压缸系统的特性。由仿真结果可得出以下结论：

(1)数字液压缸各个环节的数学模型建立准确，AMESim模型结构建立完善，且能够达到数字液压缸的反馈效果；

(2)通过对比Simulink和AMESim仿真结果曲线可知，两种仿真方式的结果曲线基本上一致，从而验证Simulink和AMESim模型的正确性；

(3)该数字液压缸的研究方法能用于对称阀控制非对称液压系统的求解，为新型数字液压缸提供一些重要参考意义；

(4)该仿真实验数据能为后期产品制造提供一些理论基础，减少实际产品的实验操作。