高速开关阀控气动位置伺服系统的模糊自适应PID控制
吴昌文,朱玉川,高 强
(南京航空航天大学 机电学院,江苏 南京 210016)
引言
气动位置伺服系统因具有无污染、响应速度快、功率-质量比大等优点,在机器人、医疗器械以及工业自动化等领域受到越来越广泛的关注[1-2]。目前,气动位置伺服系统一般采用比例阀作为控制元件以获得更好的控制效果,但由于其体积较大、结构复杂,不可避免存在成本高、使用条件苛刻等问题[3-4]。高速开关阀作为典型的数字控制元件,相对于比例阀具有结构简单、体积小、成本低等优势,在气动位置伺服系统中得到迅速的发展及应用[5]。然而,由于空气压缩性、气缸摩擦力、高速开关阀输出流量的离散性和非线性等因素使得整个系统具有较强的非线性,这对系统精确建模带来了一定的难度。采用常规的PID控制算法,虽然可以不依赖于系统模型,但由于系统的时变非线性等问题,造成控制参数整定困难以及整定后控制参数对于不同的工作条件下适用性较差,最终导致位置控制精度难以提升。
针对高速开关阀控气动位置伺服系统采用常规PID控制精度较差的问题,国内外学者在控制策略上开展了大量的研究工作。其中,改进的比例-积分-微分(PID)控制由于控制算法简单、控制性能较好、可靠性高且不依赖被控对象的精确建模,在具有严重非线性且难以建立准确模型的气动位置伺服系统中具有重要研究意义。改进的PID控制,是一类以PID控制为基础,结合一些补偿方法进行输出量补偿,或与模糊控制、神经网络控制等方法进行PID参数自整定的控制策略,能够有效提高气动位置伺服系统的控制性能[6]。VARSEVELD等[7]采用2个二位三通高速开关阀控制气缸,并提出一种PID+位置前馈+摩擦力补偿的控制策略,实现气缸的定位误差小于0.2 mm;孟宪超等[8]针对高速开关阀控气动位置控制系统,提出一种模糊控制与PI控制切换的控制策略,提高了系统的动态性能与精度;曹会发[9]等利用模糊控制器替代PID控制器中的积分环节与微分环节,与比例环节相结合,实现了气动执行器在不同条件下均有较好的控制效果;郭艳青等[10]利用BP神经网络对PID控制器的控制参数进行在线调整,实现气缸位置的高精度控制。采用智能控制算法对PID控制参数进行在线调参的方法可以减小PID参数整定的复杂性,并提高控制算法的适用性。相较于神经网络控制存在的学习和控制算法的收敛性、实时性等不确定因素,模糊控制更加易于实现,并且对于对象参数变化的适应性更强。
本研究引入模糊控制原理,根据系统的实时状态对经验法初步整定的PID参数进行调整,以满足系统动态过程中各阶段对于PID参数的不同需求。该方法避免了单一PID参数控制下由于气动位置伺服系统的时变非线性造成的控制参数整定困难、不同工作条件下适用性较差等问题。在不用对系统进行精确建模的基础上,进一步改善系统的控制性能,且减小了PID参数整定的复杂性,提高了控制器的适用性与鲁棒性。实验结果表明,通过模糊控制对PID控制参数进行在线整定,能够有效提高系统跟踪阶跃信号以及正弦信号的控制性能。
1 气动位置伺服控制系统结构与工作原理
为开展高速开关阀控气动位置伺服系统的控制策略研究,搭建了如图1所示的系统。该系统由以下几个部分组成:4个二位二通高速开关阀、1个低摩擦气缸、位移传感器、压力传感器、xPC半实物仿真平台以及相应的气源设备。
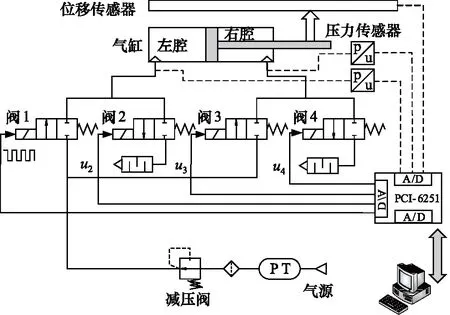
图1 位置伺服系统结构示意图
4个高速开关阀组成全桥回路以实现对气缸两腔的独立控制,并且通过对4个高速开关阀的开关状态进行逻辑控制以实现气缸的换向运动。阀的开关状态组合模式如下:模式一,阀1和阀4开启,阀2和阀3关闭,无杆腔进气,同时有杆腔出气;模式二,4个阀均关闭,气缸两腔不进气不出气;模式三,阀2和阀3开启,阀1和阀4关闭,无杆腔出气,有杆腔进气。各个高速开关阀均采用频率固定的PWM信号驱动,通过控制器输出的占空比,控制阀口开启的时间。位移传感器将系统的实时状态通过数据采集卡,经A/D转换后传输至计算机,计算机根据指令信号和状态反馈信息,经过控制器求解得到各个高速开关阀的驱动信号,并经过驱动器驱动高速开关阀,实现气缸的位置伺服控制。
2 系统的数学模型
2.1 高速开关阀建模
高速开关阀的流量模型通常采用理想气体流过收缩喷管的质量流量方程[11]表示如下:
(1)
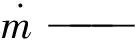
Cf—— 阀口流量系数
Av—— 阀口节流面积,m2
pu,pd—— 分别为阀口前后的气体压力,Pa
T—— 气体温度,K
γ—— 空气的比热容比
R —— 理想气体常数,J/(kg·K)-1
pcr—— 临界压力比
2.2 气缸建模
假设气缸腔内气体状态变化过程为绝热过程,同时气体温度在充放气过程中保持不变且等于环境温度。根据理想气体状态方程、质量连续性方程建立气缸腔内的压力微分方程:
(2)
式中,p—— 气缸腔内气体的压力,Pa
V—— 体积,m3
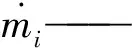
根据牛顿第二定律,气缸活塞的动力学方程为
(3)
式中,M0—— 气缸输出杆与负载的总质量,kg
pl,Al—— 无杆腔气压,Pa;有效作用面积,m2
pr,Ar—— 有杆腔气压,Pa;有效作用面积,m2
Ff—— 气缸运动过程中的摩擦力,N
Fout—— 大气作用在气缸输出杆端产生的力,N
3 位置控制策略设计
针对常规PID控制器由于参数固定不变而造成控制性能较差的问题,引入模糊控制对其改进,利用模糊控制原理,根据系统运行中实时检测得到的位置误差e及误差偏差率ec对PID控制器的比例系数Kp、积分系数Ki以及微分系数Kd进行在线调节,以满足气动位置伺服控制过程中对控制参数的不同要求。所设计的模糊自适应PID控制器基本原理如图2所示,该控制系统包含模糊控制器和常规PID控制器两部分,首先利用模糊控制器对常规PID控制器的3个参数进行在线调整,进而通过PID控制器求得系统的输入控制信号。
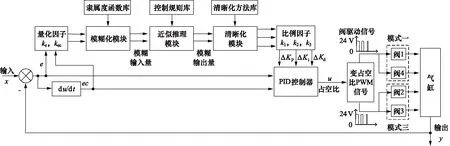
图2 模糊自适应PID算法控制原理
3.1 模糊控制器设计
模糊控制器的输入为位置误差e以及位置误差偏差率ec,输出量为PID 3个控制参数的修正量ΔKp,ΔKi,ΔKd。为方便隶属度函数的设计,将各变量的模糊子集均设置为{负大,负中,负小,零,正小,正中,正大},记为{NB,NM,NS,ZO,PS,PM,PB},相应的模糊论域均取[-6,6],通过调整输入量的量化因子ke,kec与输出量的比例因子k1,k2,k3得到各个变量的实际取值范围。其中,e和ec的隶属度函数选择梯形与三角形隶属度函数的组合,在误差和误差偏差率很大或很小时,采用梯形隶属度函数,以便获得最大的控制量;而在中间阶段,为得到更加精确的控制量,采用灵敏度较高三角形隶属度函数。输出量的隶属度函数均选取高斯隶属度函数,其具有平滑、对称且没有零点的特点。输入变量误差e和误差偏差率ec的隶属度函数A(E)和输出变量ΔKp,ΔKi,ΔKd的隶属度函数A(K)分别如图3、图4所示。接着对模糊控制规则进行设计,制定了如表1所示的模糊规则。模糊推理方法选取应用最为广泛的最大-最小模糊推理方法,而清晰化方法则选取重心法。
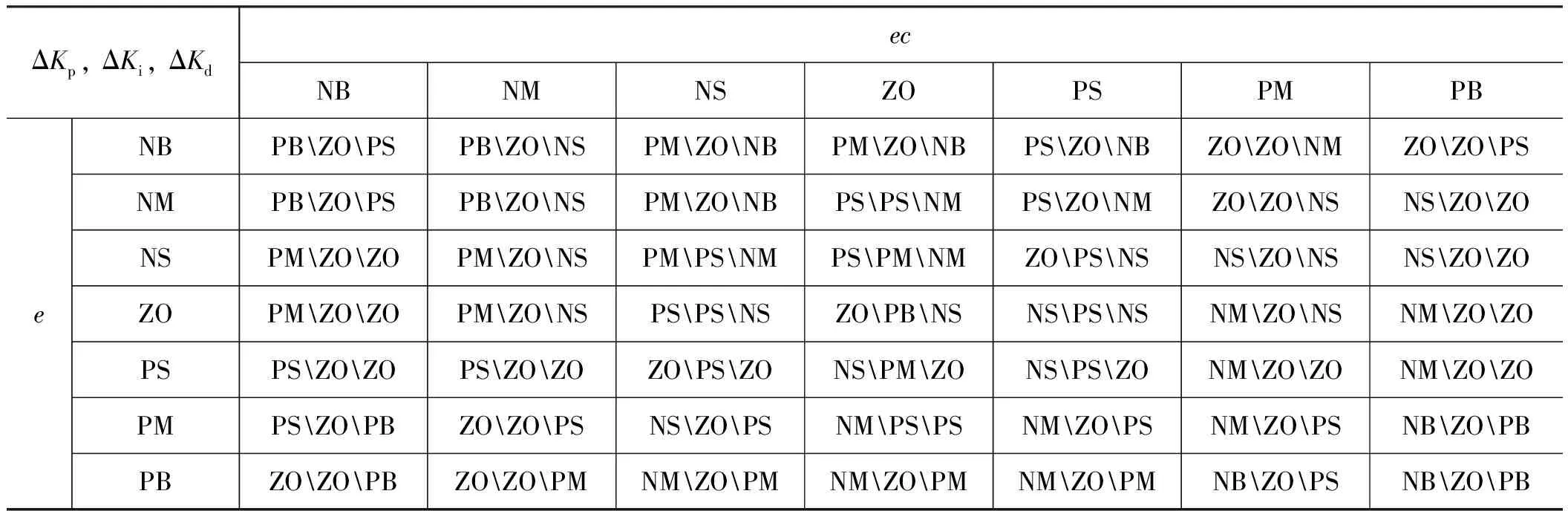
表1 模糊规则表
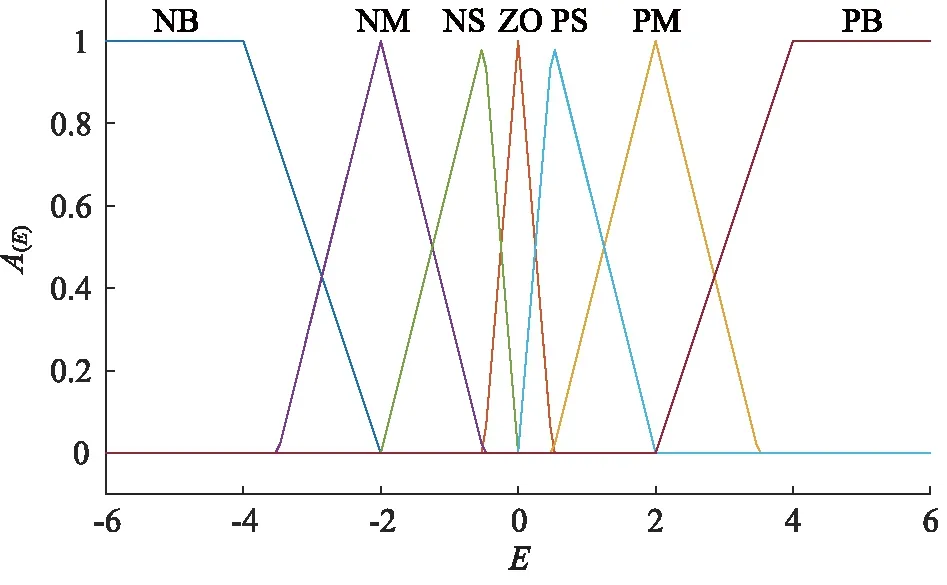
图3 输入量隶属度函数
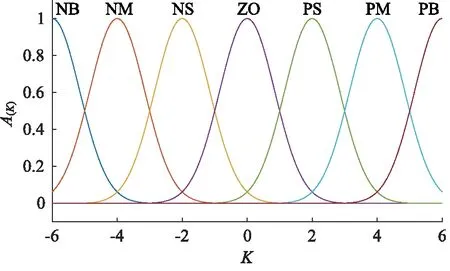
图4 输出量隶属度函数
3.2 PID控制器设计
利用上述的模糊控制策略,可根据控制过程中的实时状态输入,对PID参数进行在线调整,调整规则如下:
Kp=Kp0+ΔKp
Ki=Ki0+ΔKi
Kd=Kd0+ΔKd
(4)
式中,Kp0,Ki0,Kd0分别为PID控制器的初始值。
利用整定后的PID参数,根据检测得到的误差e(t),即可求得PWM信号每个周期对应的占空比u(t),从而实现变占空比PWM信号的输出。
(5)
4 试验分析
4.1 平台搭建
为了验证所设计的模糊自适应PID算法的控制性能,根据图1所示的系统原理图搭建了高速开关阀控气动位置伺服系统的半实物仿真测试平台,如图5所示。该系统的气源由空气压缩机提供,最高可供给0.8 MPa的气压,同时配备30 L储气罐以及压力调节范围为0~1.6 MPa的气动三联件。高速开关阀型号均为MATRIX 820系列MX 821.103C2XX二位二通常闭型,在0.4 MPa供压下阀口的最大流量可达到70 L/min,并配套高速开关阀驱动板(HSDB990.012),能够实现开启和关闭的响应时间均小于1 ms,即最大频率可达500 Hz。气缸采用SMC-MQM系列,气缸内径16 mm,行程100 mm。位移传感器量程为0~100 mm,精度为0.05%,压力传感器量程为0~0.6 MPa,精度为0.1%。xPC半实物仿真系统由PCI 6251、接口板、上位机和下位机等组成,进行数据的采集、处理和控制信号的生成、输出。
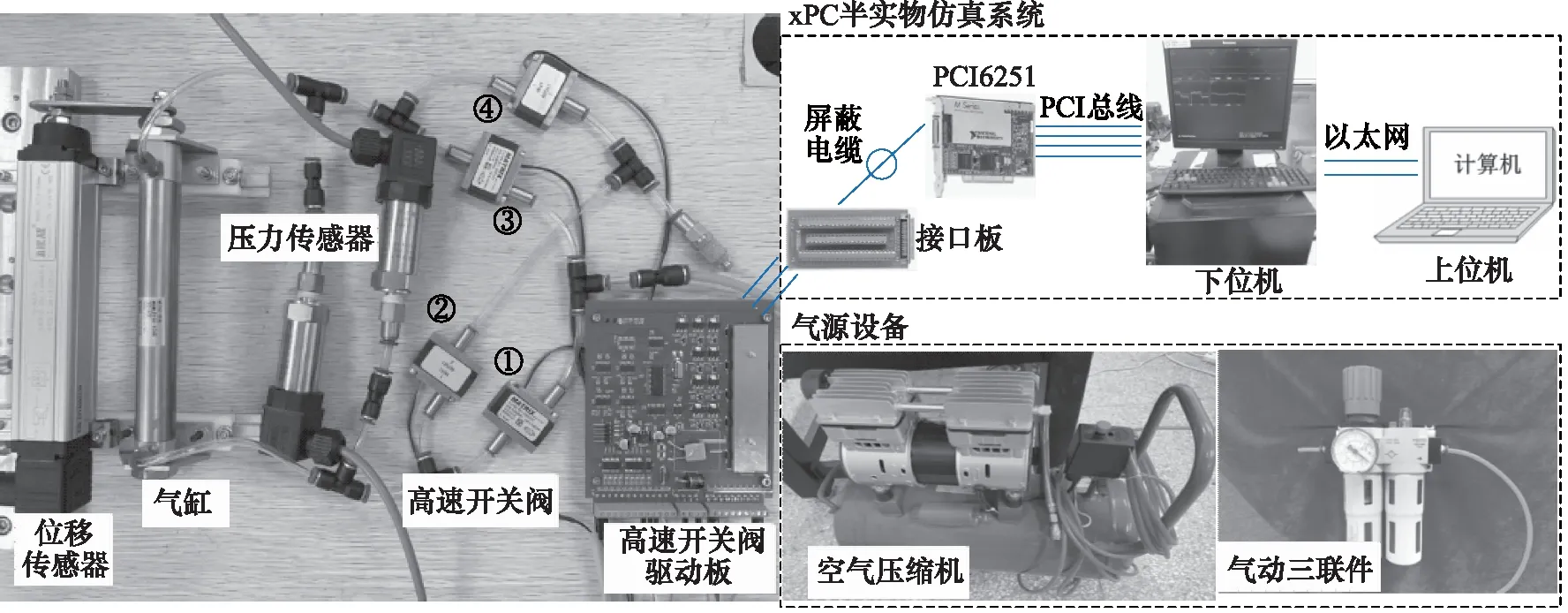
图5 高速开关阀控气动位置伺服系统的半实物仿真测试平台
4.2 实验结果分析
通过模糊自适应PID控制器与常规PID控制器对比,以验证所提出控制器算法的有效性。实验相关参数设置如下:Kp=20,Ki=8,Kd=0.1,ke=60,kec=1/6,k1=5/3,k2=5/2,k3=1/120。此外,驱动高速开关阀的PWM信号频率设置为100 Hz,供气压力设置为ps=0.4 MPa。
首先,采用常规PID控制器与模糊自适应PID控制器分别对幅值为20,40,60,80 mm 4组阶跃位置信号进行了跟踪试验,得到对应的气缸活塞位置跟踪曲线如图6所示,试验结果如表2所示。
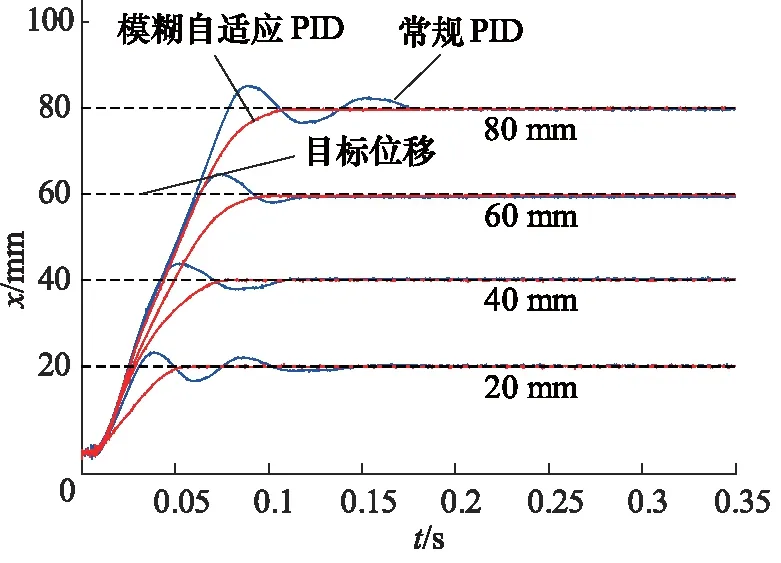
图6 阶跃跟踪试验曲线
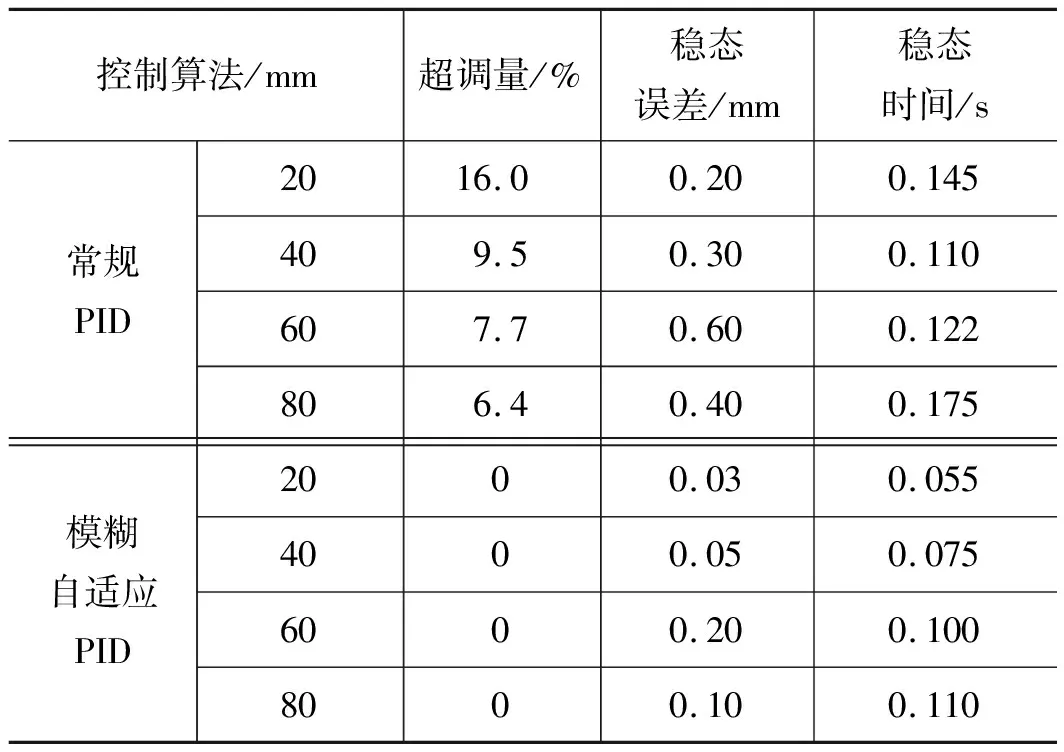
表2 阶跃跟踪试验结果
通过对阶跃跟踪的试验结果分析可知,使用模糊自适应PID控制器的气缸活塞位移无超调量,相较于常规PID控制器显著减小,且稳态误差也大幅度减小,在4组幅值阶跃跟踪中均小于0.2 mm。此外,稳态时间也得到了进一步提升,以幅值为80 mm的阶跃跟踪为例,模糊自适应PID控制器比常规PID控制器的稳态时间减少了13.7%。
其次,采用以上2种控制器跟踪幅值为30 mm,频率为0.5 Hz的正弦位置信号,其位置跟踪曲线以及误差曲线分别如图7、图8所示。由图可知,采用模糊自适应PID控制器的跟踪性能明显优于常规PID控制器。
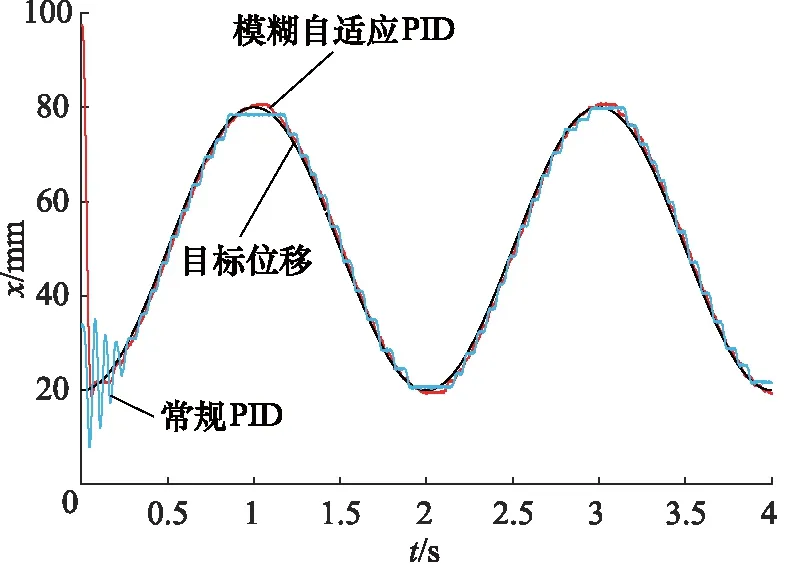
图7 正弦信号位置跟踪曲线对比
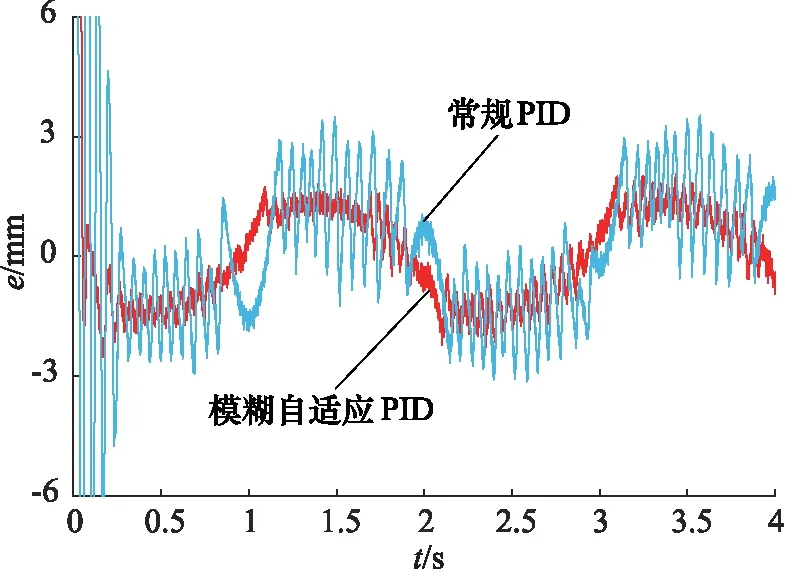
图8 正弦信号位置跟踪误差对比
为了准确评价模糊自适应PID控制策略对于正弦位置信号的跟踪性能,采用第二个周期中的最大跟踪误差Me,平均跟踪误差μe,以及标准跟踪误差σe作为性能的评价指标[12]。正弦跟踪的评价指标如表3所示。
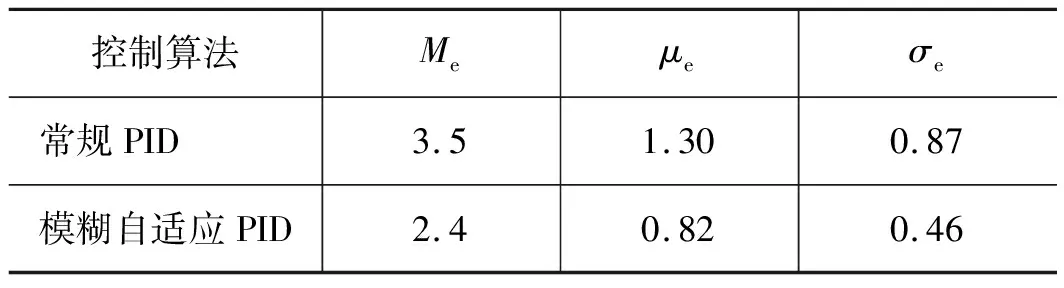
表3 正弦跟踪的评价指标 mm
(6)
式中,N为误差值的数目。
从表3中的数据可以看出,采用模糊自适应PID算法,正弦跟踪第二个周期的最大跟踪误差为2.4 mm,平均跟踪误差为0.82 mm,标准跟踪误差为0.46 mm,均小于常规PID的控制指标,控制性能明显提升。由阶跃信号以及正弦信号位置跟踪实验结果可知,采用模糊自适应PID算法能够兼顾气动位置伺服系统的动、静态特性,有效提高系统的控制精度。
5 结论
采用4个高速开关阀控制气缸的系统作为控制对象,提出了一种模糊自适应PID控制算法。搭建系统的实验平台,对所提出的算法进行了实验验证。实验结果表明,在进行阶跃信号位置跟踪时,气缸活塞位移无超调量且稳态误差均小于0.2 mm;跟踪幅值为30 mm,频率为0.5 Hz的正弦信号时,第二个周期的最大跟踪误差、平均跟踪误差及标准跟踪误差分别为2.40,0.82,0.46 mm,与常规PID控制器相比,控制性能显著提升。

