阀控单出杆缸电液伺服系统二阶线性自抗扰控制
金坤善,宋建丽,梁 涛,李永堂,仉志强
(1.太原科技大学 金属材料成形理论与技术山西省重点实验室,山西 太原 030024;2.太原科技大学 电子信息工程学院,山西 太原 030024;3.北京信息科技大学 光电工程学院,北京 100192;4.泰安华鲁锻造机械有限公司, 山东 泰安 271000)
引言
阀控单出杆缸电液伺服系统(Electro-hydraulic Servo System, EHSS)具有功率密度大、响应速度快、结构紧凑等优点,在材料成形装备[1]、航空[2-3]、机器人手臂[4]等工业控制领域得到广泛的应用。但液压缸结构的非对称性导致正、负行程的开环增益和动态特性存在明显差异,加剧了EHSS不确定性和非线性。设计一种高性能控制器,使阀控单出杆缸EHSS的运动状态和系统的工程达到所期望的稳定性、快速性、准确性和经济性等指标,成为一项具有挑战性的任务。
如何有效抑制阀控单出杆缸EHSS不确定扰动,是实现其高性能控制的首要问题。针对EHSS存在的不确定性,研究人员提出了基于EHSS精确数学模型的滑模控制[5]、H∞鲁棒控制[6]、定量反馈理论[7]、反馈线性化[8-9]、自适应控制[10-13]、基于扰动观测器控制[14-15]等控制方法,研究成果促进了这一领域的发展。少数研究工作综合考虑了包括液压缸结构非对称性导致的不确定性,文献[6]开发了一种具有积分作用的H∞控制器用于单出杆缸位置控制,但在推导不确定线性化模型时,比例阀流量增益的近似处理,导致液压缸往返运动速度增益差异被忽略;文献[10]设计了基于反步技术的自适应鲁棒控制器,用于单出杆缸活塞位移跟踪控制,该方法融合了自适应控制与鲁棒控制的优点,通过自适应系统不确定性参数,提高了系统跟踪精度,完善了鲁棒控制结构,避免了自适应控制引起的系统不稳定问题,但估计参数过多、应用复杂。基于扰动观测器的控制方法,根据系统特性设计扰动观测器,实现不确定扰动的重构,利用扰动前馈补偿来抑制不确定扰动对控制性能的影响,但该控制方法严重依赖模型精度;反馈线性化方法不仅需要精确数学模型,还需提供系统状态信息,且控制律比较复杂。工程实践中,精确数学模型往往很难获取或获取成本过高,采用上述控制方法设计的控制器,由于模型不匹配容易导致控制器性能下降,甚至失稳。
本研究提出一种具有加速度前馈的阀控单出杆缸EHSS LADRC策略,将建模误差、外部扰动、传感器测量噪声等不确定扰动视为系统总扰动,并定义为系统扩张状态,利用三阶线性扩张状态观测器(Linear Extended State Observer,LESO),实现包括总扰动的系统状态在线估计,并利用LESO滤波特性,抑制传感器高频测量噪声。单出杆缸EHSS经扰动前馈补偿后,转化为理想的二阶积分级联形式,实现了动态模型的不变性,进而完成状态误差反馈控制律设计,最终实现活塞位移对给定信号的高性能跟踪控制。
1 系统结构与动态模型
阀控单出杆缸EHSS由单出杆液压缸、油源、三位四通电磁比例阀、直线位移传感器、负载及其他辅助元件组成,如图1所示,其中ps,pr分别为油源压力、回油压力;A1,A2分别为无杆腔与有杆腔活塞面积;V10,V20分别为无杆腔、有杆腔初始容积,V1=V10+A1x,V2=V20-A2x,x为活塞位移;p1为无杆腔压力,p2为有杆腔压力;m为等效负载质量;FL为外部扰动;xv为阀芯位移;u为电磁比例阀输入电压。
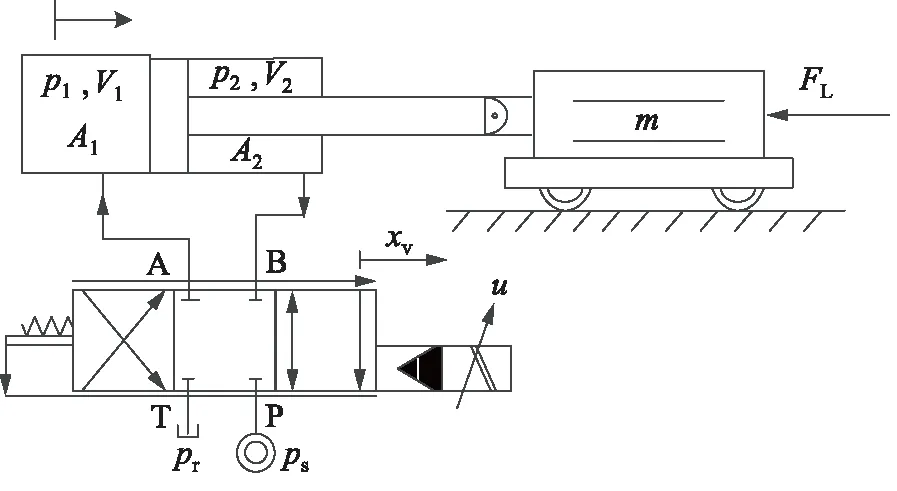
图1 阀控单出杆缸电液伺服系统
考虑到电磁比例阀动态响应速度远高于液压缸工作频率,忽略阀的动态特性,电磁比例阀阀芯位移与控制输入满足:
(1)
式中,kv>0,为比例阀增益。
根据牛顿第二定律,阀控单出杆液压缸动态方程可以表示为:
(2)
式中,Bp—— 黏性摩擦系数
K—— 负载刚度
x—— 活塞位移
忽略外部泄漏,液压缸两腔压力动态方程:
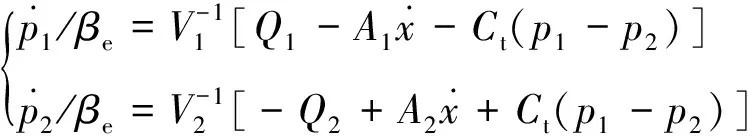
(3)
式中,Ct—— 液压缸内漏系数
βe—— 油液弹性模量
Q1—— 比例阀流入液压缸无杆腔流量
Q2—— 有杆腔流入比例阀的流量
定义切换函数:
(4)
比例阀输入、输出流量Q1,Q2可表示为:
(5)

将式(1)代入式(5)有:
(6)
定义:
γ=kqkv
(7)
(8)
将式(7)、式(8)代入式(6)有:
Q1=γR1u,Q2=γR2u
(9)
将式(9)代入式(3)有:
(10)
液压缸活塞驱动力可以表示为:
F=p1A1-p2A2
(11)
综合式(2)、式(10)、式(11)可得:
(12)
其中,Δ为未建模态,b0为控制增益b的估计值。
式(12)表明:阀控单出杆缸EHSS是一个多变量、强耦合非线性时变不确定系统,存在参数摄动、时变负载、建模误差等多源不确定扰动。
2 具有加速度前馈的二阶LADRC设计
LADRC主要由跟踪微分器(Tracking Differentiator,TD)、LESO、线性状态误差反馈控制器(Linear State Error Feedback Controller,LSEFC)三部分构成。TD用于获得理想的暂态过程,LESO实现包括总扰动的系统状态在线估计,LADRC通过扰动前馈补偿,将不确定非线性系统转换为二阶积分级联形式,LSEFC进一步抑制不确定扰动,实现系统高性能控制。阀控单出杆EHSS二阶LARC控制系统结构如图2所示。

图2 二阶LADRC结构图
根据控制性能要求设计三阶线性跟踪微分器[16]具有如下形式:
其中,r大于0为速度因子,取值越大跟踪响应速度越快;v为待跟踪信号;v1,v2,v3分别为EHSS期望的位置、速度和加速信号。
2.1 三阶LESO的构建
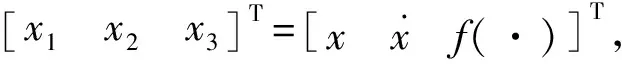
y=Cx
(14)
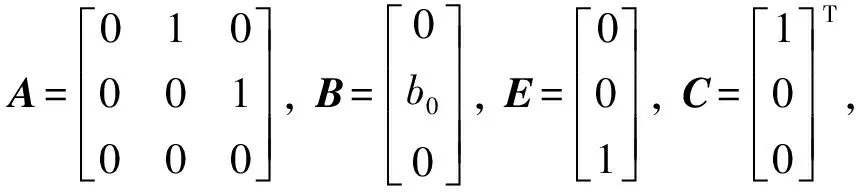
根据状态空间方程(14),三阶LESO可表示为:
(15)
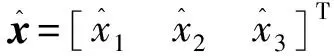
三阶LESO特征多项式:
λ(s)=|sI-(A-LC)|
(16)
为方便起见,特征多项式极点配置于-ωo,则λ(s)=|sI-(A-LC)|=s3+l1s2+l2s+l3=(s+ωo)3为霍尔维茨多项式,且:
此时,LESO增益被转化为观测器带宽ωo。
2.2 加速度前馈状态反馈控制律
若总扰动能被三阶LESO实时估计,将控制律:
(18)
代入系统式(12),不确定EHSS可近似为二阶积分串联系统:
(19)
其中,u0为虚拟控制信号,为提高系统响应速度,采用具有加速度前馈的比例微分控制律:
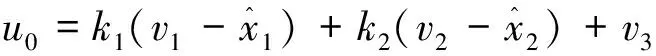
(20)
其中,k1,k2为状态误差反馈控制增益系数,当等式s2+k2s+k1=(s+ωc)2成立时:
(21)
控制器带宽ωc取值越大,响应速度越快,稳态误差越小[1],系统硬件配置要求也就越高。因此ωc取值需在控制系统性能与成本之间进行适当折中。
2.3 EHSS二阶LADRC稳定性分析
定义三阶LESO状态估计误差向量为:
(22)
根据式(14)、式(15),状态估计误差动态可表示为:
(23)

(24)
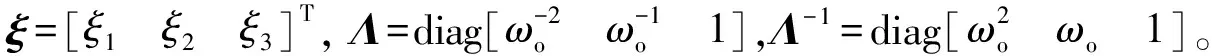
定义:ε=1/ωo,并将式(24)代入式(23),LESO状态估计误差动态可表示为:
=Αεξ+εEη
(25)

式(25)表明:由η描述的EHSS不确定扰动将被ε抑制,即增大观测器带宽ωo将减少η对观测器动态误差的影响。
定义活塞状态跟踪误差向量:
(26)
其中,e1为活塞位移跟踪误差,e2为速度跟踪误差。

(27)
并将式(12)代入式(27),EHSS闭环状动态误差可以表示为:
(28)
根据式(18)~式(21)、式(26)~式(28),控制器输出可表示为:
(29)

将控制器式(29)代入误差动态方程式(28),并根据式(24),系统状态误差动态可表示为:
(30)
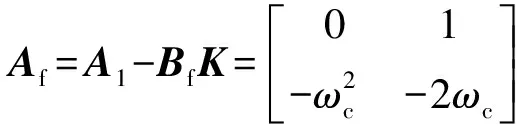
(31)
结合状态估计误差动态式(25)和系统状态反馈误差动态式(30),系统闭环误差动态可以表示为:
(32)
由于LESO动态响应速度远高于状态反馈控制器响应速度,式(32)所描述的EHSS构成了具有不同时间尺度的奇异摄动微分方程线性系统。
在工程实践中,总扰动f及其导数η未知但一定有界,且f(·)|t=0=0,η(·)|t=0=0,满足利普希茨条件。根据文献[17],存在ε*>0,对于所有ε<ε*,二阶LADRC控制作用下的单出杆缸EHSS是指数稳定的。
3 仿真与实验研究
为了验证所提出控制策略的可行性与有效性,综合考虑系统外部扰动、建模误差以及传感器测量噪声等多源不确定扰动的影响,选用工业控制领域占主导地位的PID控制进行对比仿真分析和实验研究。根据实际工况,阀控单出杆缸EHSS主要物理参数标称值如表1所示。

表1 阀控非对称缸电液伺服系统物理参数
3.1 阀控单出杆EHSS仿真分析
基于动态数学模型式(12),搭建MATLAB/Simulink仿真模型,PID控制器参数采用临界比例度法整定,其中kp=0.012,ki=0.0009,kd=0.0001。二阶线性LADRC控制器参数选用b0=4.5×105,ωc=35 rad/s,ωo=100 rad/s。
仿真结果如图3所示,二阶LADRC控制的EHSS阶跃响应稳态误差0.1 mm远小于PID控制时0.4 mm,动态跟踪误差1.8 mm也低于后者2.4 mm;5 s后随着交变脉宽扰动引入及系统参数摄动,LADRC的控制性能几乎保持不变,但PID控制性能急剧下降。

图3 扰动作用下阶跃响应曲线对比
为进一步验证系统抗扰性能,选用不同频率的正弦信号作为跟踪信号,模拟不同往返速度时活塞位移跟踪性能,仿真结果如图4所示。
仿真结果表明:当跟踪信号频率(ω=0.5)时,LADRC和PID二者均能确保EHSS稳定,但PID作用下的最大跟踪误差为2 mm,明显大于LADRC时的0.1 mm,如图4a所示。随着跟踪信号频率增大(ω=2,π),尽管LADRC控制作用下系统稳态误差有所增加(2 mm增大至5 mm),但仍能确保系统稳定运行。而常规PID控制作用下的系统出较为明显的振荡甚至失稳,如图4b、图4c所示。
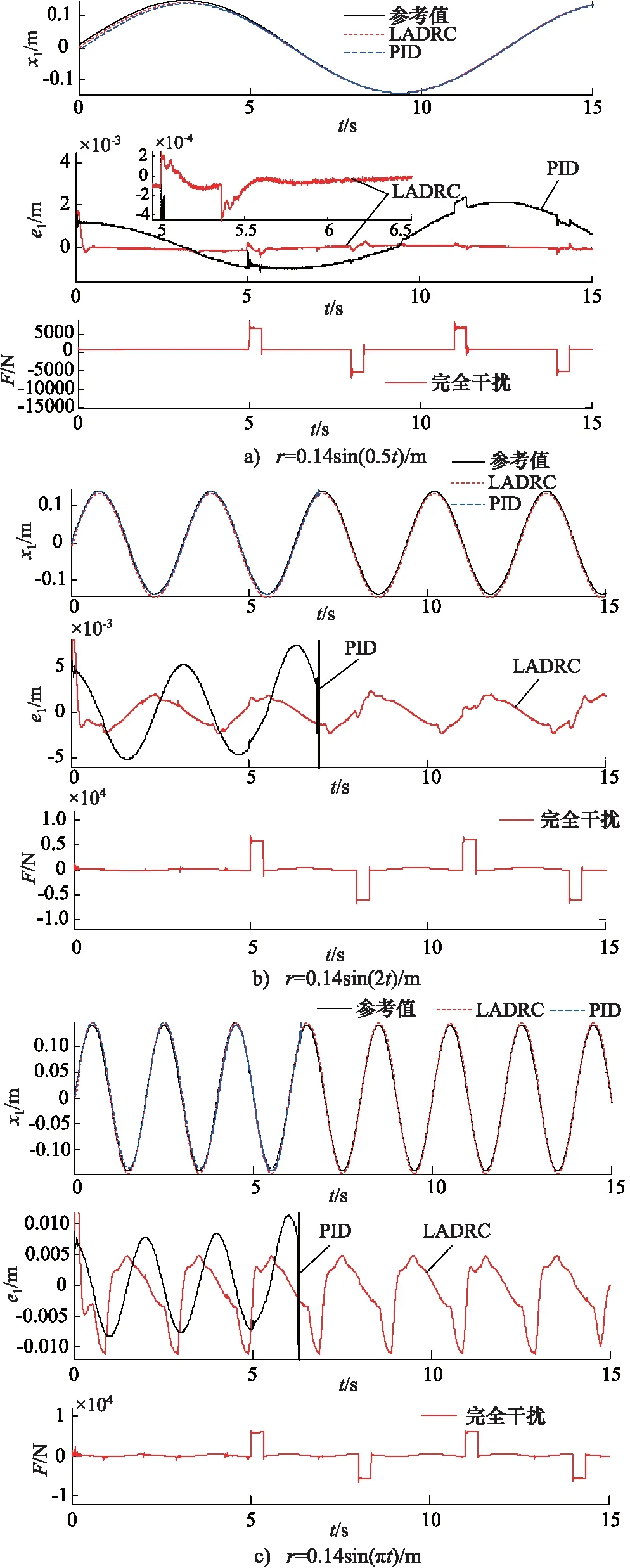
图4 扰动作用下正弦响应曲线对比
3.2 实验验证
为了验证本研究所提出的控制方法的有效性,搭建了阀控单出杆缸EHSS实验平台,并进行实验研究,实验原理如图5所示。
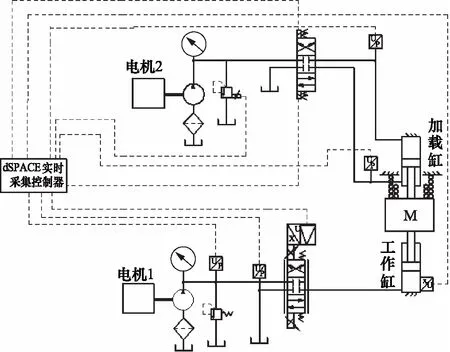
图5 阀控单出杆缸EHSS实验原理图
根据实验原理图搭建实验系统如图6所示,是由两路恒压油源、台架、2个单出杆液压缸、负载质量块、基恩士磁悬浮直线位移传感器(1800X10400)、三位四通电液比例阀(4WREE10V-75-7X/6EG24N9K31/AV)、比例溢流阀(DBEE10/5X-315YG24K31K4M)等组成。

图6 阀控单出杆缸实验系统
直线位移传感器完成活塞位移的实时采集,输出0~10 V模拟电压信号,经A/D转换后反馈至dSPACE实时采集控制器。双极性D/A转换器将控制器输出的数字信号转换为-10~10 V的模拟电压信号,并作用于三位四通电磁比例阀,完成阀口与开度的调节,实现流入/流出液压缸两腔流量的调节,最终实现驱动缸活塞位移控制。外部不确定扰动通过调节溢流阀开度实现。
(1)要求活塞4 s内抵达118 mm,实验结果如图7所示。实验结果表明:在不确定扰动作用下,LADRC和常规PID两种控制策略均能实现阀控单出杆缸EHSS位移的精确控制,但LADRC控制作用下的系统动态跟踪误差(1.5 mm)明显小于PID(3 mm),且稳态误差(0.5 mm)也优于后者(1 mm)。实验与仿真结果完全一致,结果表明具有加速度前馈的二阶LADRC控制方法能实现阀控单出杆缸EHSS快速、精确抵达指定工艺位置,对不确定扰动且具有较强的鲁棒性。
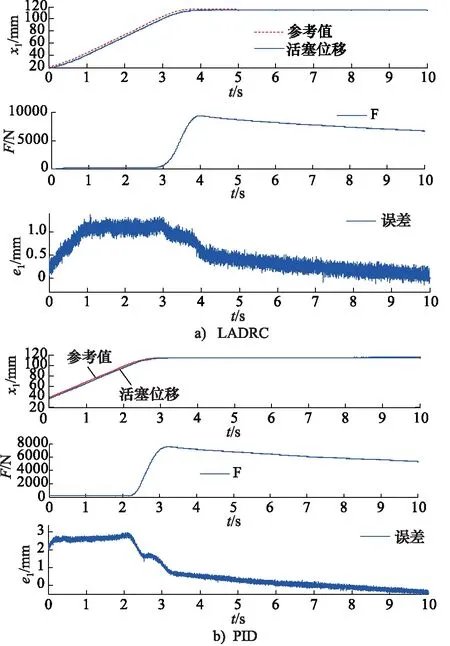
图7 LADRC和PID控制活塞位移实验结果对比
(2)为进一验证所提出LADRC控制策略动态跟踪性能,在活塞行程区间内(0~120 mm)展开跟踪控制实验,并与PID控制作用下的EHSS进行对比,实验结果如图8所示。结果表明,当系统外部扰动幅值一致,但扰动频率提升的情形下,具有加速度前馈的二阶LADRC仍能确保活塞位移快速、精确抵达期望工艺位置,且跟踪误差维持在小范围内(-2~1 mm)波动,优于PID(-2~2.5 mm)。实验结果进一步验证了所提出的控制策略对单出杆缸EHSS存在的多源不确定扰动,特别是外部时变载荷具有较强的鲁棒性。

图8 活塞往返运动跟踪性能对比
综上所述,具有加速度前馈的二阶LADRC能满足阀控单出杆缸EHSS高性能控制要求,相对传统PID控制具有较强的鲁棒性,能实现活塞位移所期望的稳定性、快速性、准确性要求。
4 结论
本研究针对单出杆缸电液伺服系统存在的多源不确定扰动抑制问题,从工程实践出发,建立了液压伺服系统动态机理模型,提出了一种具有加速度前馈的二阶线性自抗扰策略,证明了LADRC控制作用下电液伺服系统的指数稳定性,通过数值仿真和实验,得出以下结论:
(1)该控制方法具备传统PID控制不依赖于系统精确数学模型的优点,控制系统结构简单,控制器参数ωc,ωo具有明确工程物理意义,易于整定、便于工程实现;
(2)与传统PID控制相比,具有加速度前馈的二阶LADRC控制策略降低了系统中存在的多源不确定性扰动对控制性能的影响,提升了系统控制性能;
(3)将具有加速度前馈的二阶LADRC应用于阀控单出杆缸这一类EHSS中,借助于其良好的抗扰性能和动静态跟踪特性,将有利于扩大非对称缸工况适用范围,提升产品加工质量、提高生产效率、降低生产能耗、节约生产成本。

